PROBABILISTIC APPEARANCE-BASED NAVIGATION OF A
MOBILE ROBOT
Controlling a Robot in Route Following
Luis Payá, Oscar Reinoso, Arturo Gil, M. Asuncion Vicente and Jose L. Aznar
Departamento de Ingeniería de Sistemas Industriales, Miguel Hernández University
Avda. de la Universidad s/n, 03202 Elche (Alicante), Spain
Keywords: Robot Vision, Incremental PCA, Markov Localization, Collaborative Robotics.
Abstract: In this work, a solution to the problem of multi-robot following routes is proposed using an appearance-
based method. In this approach, several images are stored along the route to follow, using an uncalibrated
forward-looking camera. To extract the most relevant information, an incremental PCA process has been
implemented. This incremental process allows adding new locations to the PCA database without necessity
of creating it from the scratch. Then, the follower robots can follow the route while a leader one is still
recording it. These follower robots, using this database, make first an auto-location process to know their
current position and then a control phase to compute the necessary steering speed to tend to the route and
follow it till the end. Both speeds are obtained also through the visual information in an appearance-based
approach. The problem of ‘visual aliasing’, typical in office environments, is avoided with a probabilistic
approach that, using a Markov-process model, makes the localization more robust. The experimental results
have shown how this is a simple but robust and powerful approach for routes in an office environment.
1 INTRODUCTION
In the last years, some applications that require the
use of a team of robots have emerged. They require
the coordination between the members of the team.
In some applications, the use of collaborative
robotics clearly improves the performance,
comparing to a single robot carrying out the same
task. As an example, (Thrun, 2002) presents a
probabilistic EKF algorithm where a team of robots
builds a map online, while simultaneously they
localize themselves. (Fenwick, 2002) takes into
account the problem of the concurrent mapping and
localization with extra positional information
available when multiple vehicles operate
simultaneously. In (Ho, 2005), a map is built using
visual appearance. From sequences of images,
acquired by a team of robots, subsequences of
visually similar images are detected and finally, the
local maps are joined into a single map.
A typical problem in collaborative robotics
implies a path following e.g. to perform a
surveillance task in an office environment or an
assembly or delivery task in an industrial
environment. Also, the problem of formations,
where a team of robots must navigate keeping a
relative position in a structure of robots, can be seen
as a problem of path following, where one or several
robots must follow the path the leader is recording.
In the case of route following, to carry out the
navigation of a robot from one point to another in an
environment, a map is required. In the last years,
intensive research on this field, using SLAM
techniques (Simultaneous Localization And
Mapping) has been developed. This approach tries to
build a global map of the environment while
simultaneously determining the location of the robot.
Usually, these approaches rely on the extraction of
several landmarks or characteristic points of the
environment both natural or artificial, as (Thrun,
2002) does.
However, the problem of route following can
be solved without necessity of creating complex
maps of the environment. It is just needed a teaching
step, where the route to follow is learned, and a
navigation step, where the second robot follows the
route just comparing its current sensory information
with the data stored in the database. Classical
approaches in this field are model-based approaches,
where the extraction of several landmarks or feature
391
Payá L., Reinoso O., Gil A., Asuncion Vicente M. and L. Aznar J. (2008).
PROBABILISTIC APPEARANCE-BASED NAVIGATION OF A MOBILE ROBOT - Controlling a Robot in Route Following.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 391-398
DOI: 10.5220/0001085303910398
Copyright
c
 SciTePress

points along the images allows computing the image
Jacobian, that relates the change of the coordinates
in the image with the changes in motion in the
ground plane. Then, using the principles of visual
servoing, the second robot can follow the route, as in
(Burschka, 2001). Also, in the behaviour-based
control (Balch, 1998), some features of the images
are extracted to carry out the localization and
navigation of the members of a team in a formation
problem. However, other approaches suggest that
these processes could be achieved just comparing
the general visual information on the images,
without necessity of extracting any feature. These
appearance-based approaches are specially useful for
complicated scenes in unstructured environments
where appropriate models for recognition are
difficult to create. As an example, (Matsumoto,
1999) addresses a method consisting on the direct
comparison of low-resolution images. This method
may lead to errors when the size of the route is quite
long so other features must be added to make the
method more robust, such as histogram, texture and
density of edges, (Zhou, 2003). However, these
features contain no geometric information so they
are useful just for localization but not for navigation.
When working with the whole images, the
complexity of the problem can be reduced by means
of the PCA (Principal Components Analysis)
subspace as in (Kröse, 2004) or (Maeda, 1997),
where through PCA techniques a database is created
using a set of views with a probabilistic approach for
the localization. In classical PCA approaches, all the
views along the route must be available before the
compression can be done so the navigation of the
second robot cannot begin until the leader has
finished learning the route. Actually, a new model
must be built from the scratch when we want to
include information about new locations in the map.
These problems can be overcome using an
incremental PCA method, as shown in (Payá, 2007).
In this paper, we present an appearance-based
method for route following where incremental PCA
has been used to build the database, and a
probabilistic Markov process has been implemented
for robot localization during the navigation. First,
the representation of the environment along the route
is detailed. Then, in section 3, the basics of
localization and control in route following are
outlined. In the 4th section, the probabilistic
approach to make navigation more robust is
presented and to finish, the results and conclusions
of the work are shown.
2 REPRESENTATION OF THE
ENVIRONMENT
The philosophy of the appearance-based methods
consists in working with the general visual
information of the images, without extracting any
interesting point. Thus, this family of methods
presents the disadvantages of the size of the database
necessary to retain all the information of the
environment and the computational cost of the
comparisons between the whole images.
When working with 64x64 images, the data
vectors fall in a 4096 dimensional space. However,
all these data are generated from a process with just
three degrees of freedom (position and orientation of
the robot). This way, before storing the images, a
reduction of the dimensionality of the data can be
performed with the goal of retaining the most
relevant information of each scene. Since pixels tend
to be very correlated data, a natural reduction step
consists on performing Principal Components
Analysis (PCA), as in (Kirby, 2001).
Each image
N
j
x
M
x
j
K
r
1;
1
=
ℜ
∈
, being M the
number of pixels and N the number of images, can
be transformed in a feature vector (also named
projection of the image)
N
j
p
K
x
j
K
r
1;
1
=ℜ
∈
, being K
the PCA features containing the most relevant
information of the image,
.
N
K
≤
In traditional PCA,
first of all, the data matrix is built using the images
of the environment. The PCA transformation is
computed from the covariance of the data matrix
using SVD and the Turk and Pentland’s method
(Turk, 1991). After the process, a new data matrix
with the most relevant information is obtained.
In classical PCA approaches, all the images
along the environment must be available before
carrying out the compression. This way, the robots
that follow the route should wait the leader one to
run till the end. However, in collaborative tasks, it is
usual that some robots follow the first one while it is
still recording the information. Then, with this
approach, the robot that is building the database
should do it from the scratch when a new image
along the route is captured, what is computationally
very expensive. To overcome this disadvantage, a
progressive construction of the database can be
implemented, using the incremental PCA algorithm
exposed in (Artac, 2002). When the leader captures
a new image, it is added to the database, updating all
the projections that were previously stored.
As can be proved, when having a set of
eigenvectors from a set of views, when a new image
is added to the database, these eigenvectors and the
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
392

projection of the existing images can be updated
following the next four-step algorithm (Artac, 2002):
1. First, the mean must be updated with the
expression:
()
.
1
1
'
1+
+⋅
+
=
N
xmN
N
m
rrr
(1)
2. Now, the set of eigenvectors must be updated so
that they include the information of the new image
1+N
x
r
. To do it, we compute the residual vector, that is
the difference between the reconstruction and the
original N+1 image
()
111 +++
−+⋅=
NNN
xmpVh
r
r
r
r
. This
vector is orthogonal to the old eigenvectors. Then, it
must be normalized (so that it becomes a unit
vector), obtaining
1
ˆ
+N
h
r
.
3. The new matrix of eigenvectors
'
V
can be
obtained by appending
1
ˆ
+N
h
r
to
V
and rotating them,
according to the next expression:
.
ˆ
'
1
RhVV
n
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⋅=
+
r
(2)
being
R
the solution to the eigenproblem
'Λ⋅=⋅
R
R
D
and D is:
()
.
1
00
0
1
2
2
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⋅⋅
⋅
+
+
⎥
⎦
⎤
⎢
⎣
⎡
Λ
⋅
+
=
δδ
δ
T
T
T
p
ppp
N
N
N
N
D
r
rrr
r
r
(3)
where
()
mxh
NN
r
v
r
−⋅=
++ 11
δ
,
(
)
m
x
V
p
N
T
r
v
r
−⋅=
+1
and
Λ
is a
diagonal matrix containing the original eigenvalues.
This way, if
MxK
V ℜ∈
, then
()
1
'
+
ℜ∈
KMx
V
. It must be
studied whether this new dimension is significant or
not. In this work, two different criteria have been
used with this goal. First, if the last eigenvalue is
under a percentage of the first one, it is considered
that it does not retain enough information so the last
eigenvector is removed of the system. Also, if the
new image can be correctly represented by the
previous set of eigenvectors, the new dimension is
not added. To know it, the module of the residual
vector is computed. If this module is under a
threshold, the new image can be represented with
enough accuracy with the previous set of
eigenvectors so the new dimension is not taken into
account.
4. The image representations can be updated with
the next expression:
()
()
()
[
] ()
.'
0
'
11
mmhV
p
Rp
T
N
Ni
T
Ni
rr
r
r
r
−⋅⋅+
⎥
⎦
⎤
⎢
⎣
⎡
⋅=
++
(4)
Then, when a new image arrives, the previous
projections in the database and the eigenvectors are
updated and the new projection is added. This
method has shown to be efficient in robot navigation
(Payá, 2007).
3 LOCALIZATION AND
CONTROL FOR ROUTE
FOLLOWING
Once the database is created, one robot can follow
the route running successively two tasks: auto-
localization and control.
Auto-localization: The robot captures an image
and using this information it must decide which of
the set of the observations is the closest one. A
projection of the current image on the current
eigenspace calculated by the leader allows
determining it. This returns a K-components vector
that contains the main information of the view.
Then, this vector has to be compared with those
stored in the database. The one that offers the
minimum Euclidean distance is the matching one. It
is taken as the current position of the robot.
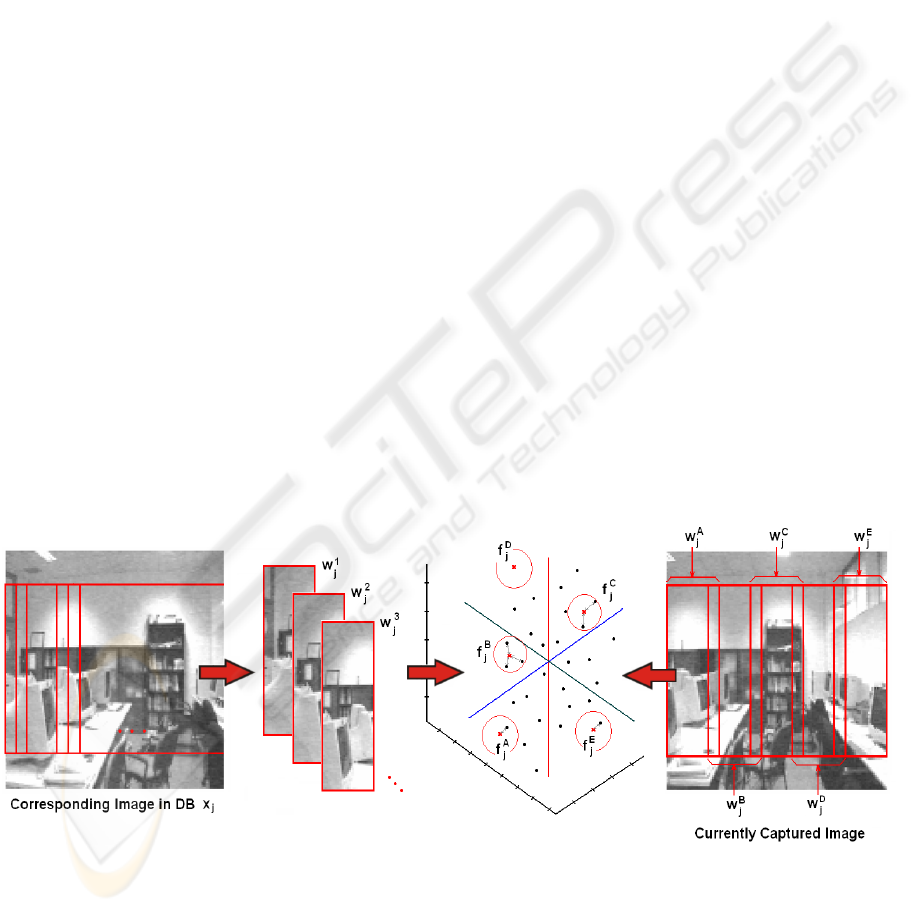
Control: From each image stored in the
database, j, a set of N’ sub-windows is obtained from
the whole image where
,
1'
x
M
i
j
w ℜ∈
r
is each sub-
window. The sub-windows are obtained scanning
the original scene with a step in the horizontal axis
(fig. 1(a), 1(b)). Carrying out a process of PCA
compression, the PCA components
,
1'
x
K
i
j
f ℜ∈
r
of
each sub-image are calculated, where K’ ≤ N’. Fig.
1(c) shows these projections as black dots in the case
K’=3. During the autonomous navigation, five sub-
windows
(
)
E
j
D
j
C
j
B
j
A
j
wwwww
r
r
r
r
r
,,,,
are taken on the
currently captured view (fig. 1(d)) and tracked over
the central band of the matching image. To do this,
once the robot knows its location, the PCA
components of these five sub-windows are
calculated. This operation returns five K’-
components vectors
(
)
E
j
D
j
C
j
B
j
A
j
fffff
r
r
r
r
r
,,,,
that are
shown as red crosses on fig. 1(c). Then, the most
similar projections to each of them are extracted.
These most similar projections are those that fall in
five spheres whose centers are
(
)
E
j
D
j
C
j
B
j
A
j
fffff
r
r
r
r
r
,,,,
.
The radius of these spheres is chosen so that a
number of corresponding windows is extracted. In
this work, a total number of seven sub-windows are
extracted. The linear and steering velocities are
inferred using a controller, whose inputs are the
most similar projections to each of the five sub-
windows. Analyzing these data and solving possible
inconsistencies, the controller infers the linear and
PROBABILISTIC APPEARANCE-BASED NAVIGATION OF A MOBILE ROBOT - Controlling a Robot in Route
Following
393

steering velocities of the robot to tend to the
recorded route.
To do it, once the most similar sub-windows
are recognized, the controller tries to arrange them
and look for a correlation that shows clearly if the
robot has to turn left or to turn right to tend to the
pre-recorded route.
Fig. 2 shows an example of how the controller
works. In this figure, the blue crosses are the seven
most similar sub-windows. On this figure, the most
similar window to
A
j
w
r
is the window 8
(
)
8
j
w
r
, the
most similar to
B
j
w
r
are the windows 12, 13 and 14
(
)
141312
,,
jjj
www
rrr
, the most similar to
C
j
w
r
are 15 and 16
(
)
1615
,
jj
ww
rr
,
D
j
w
r
has no correspondences and the most
similar to
E
j
w
r
is the 3rd window
(
)
.
3
j
w
r
This
distribution of correspondences shows that the robot
has to turn left so that the sub-windows fit with
those of the corresponding image. The
correspondence of
E
j
w
r
has been considered as an
outlier so it has been discarded. Actually, this is a
wrong point due to the fact that this window falls out
of the image
j
x
r
. The steps that are followed to
deduct the value of the control action are are:
1. Several least-squares fittings are done using the
following data at each fitting:
- Correspondences of the 2 first sub-windows.
- Correspondences of the 3 first sub-windows.
- Correspondences of the 4 first sub-windows.
- All the correspondences.
- Correspondences of the 4 last sub-windows.
- Correspondences of the 3 last sub-windows.
- Correspondences of the 2 last sub-windows.
2. The most confident fitting of the previous ones is
chosen. The criteria used to choose it are the number
of correspondences used to do the fitting, the
confidence and the slope of the fitted line (in this
work, the slope has to be near to N’/5).
3. The ordinate at the origin of the chosen linear
regression shows how the steering of the robot
should be to tend to the route correctly. If it is
positive, the robot must turn left and if it is negative,
the robot must turn right.
4. To improve this controller, a detector of outliers
has been added so that they are removed before
computing the final linear regression.
Fig. 3 and fig. 4 show two additional examples
of distributions and the least squares fitted line that
has been computed. On fig. 3, all the points are used
to make the fitting and an outlier has been detected
at position
D
j
w
r
. In this case, the robot has to go
straight to follow the route. On fig. 4, the windows
corresponding to
D
j
w
r
and
E
j
w
r
have been used and an
outlier has been detected. As a result, the robot has
to turn right to follow the route, with a steering
proportional to the ordinate in the origin.
(a) (b) (c) (d)
Figure 1: Calculating the linear and steering speeds of the follower robot. When it captures a new image, five sub-windows
are extracted and tracked over the corresponding image in the DB. The most similar projections are the inputs of a
controller that computes the necessary speeds of the robot.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
394

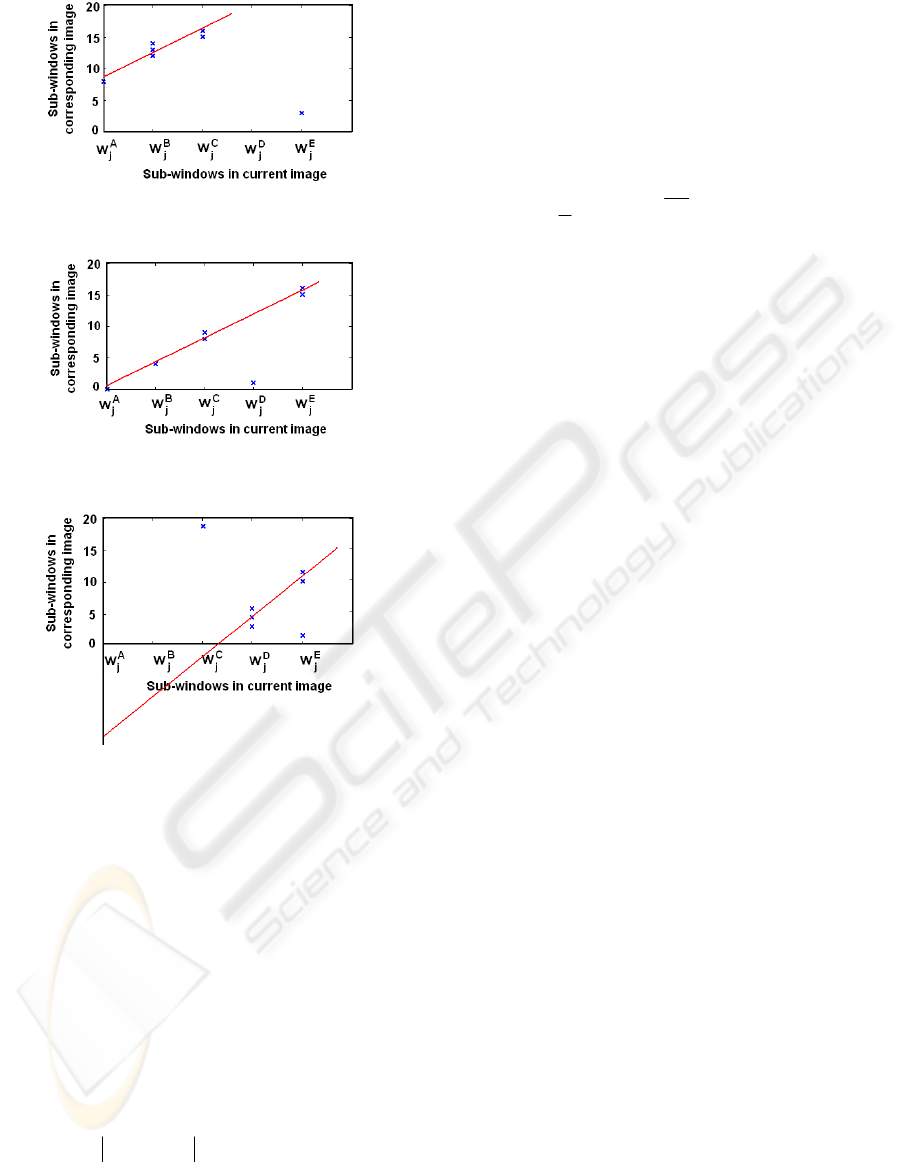
Figure 2: Calculation of the control action. Case 1: in this
case, the robot has to turn left to follow the route.
Figure 3: Calculation of the control action. Case 2: the
robot has to go straight to follow the route.
Figure 4: Calculation of the control action. Case 3: the
robot has to turn right to follow the route.
4 IMPROVING VISUAL PATH
FOLLOWING
In office environments, the simple localization
method exposed tends to fail often as a result of
‘visual aliasing’. This means that the visual
information captured at two different locations that
are far away can be very similar. To avoid these
problems, a probabilistic approach, based on a
Markov process, has been used. The current position
of the robot can be estimated using the Bayes rule:
()() ()
.;; xpxzpzxp ⋅∝ θθ
(5)
where p(x) denotes the probability that the robot is
in the position x before observing z. This value is
estimated using the previous information and the
motion model. p(z|x) is the probability of observing
z if the position of the robot is x. This way, a method
to estimate the observation model must be deducted.
In this work, the distribution p(z|x) is modeled
through a sum of Gaussian kernels, centered on the k
most similar points of the route:
()
.1;
1
|
1
2
Nje
k
xzp
k
i
xx
j
j
K=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⋅⋅=
∑
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
σ
γ
(6)
Each kernel is weighted by a value of
confidence
[
]
,1,0
∈
j
γ
that depends on the degree of
similarity of the projection of the current image with
the projections in the database. Then, these kernels
are convolved with a Gaussian function that models
the motion of the robot (knowing the previous
position and velocity of the robot). At last, the
contribution of each resulting kernel,
,
j
c
is
computed on each point, and the new position is
considered at the point with highest contribution
.
max
j
c
Fig. 5 shows this process for k=5 kernels. First,
the five most similar positions are selected. Then, a
kernel function is assigned to each position. After
that, the motion model is applied and at the end, the
contribution of each kernel to each position is
computed, selecting the point with the maximum
contribution.
This method works well only if a robust initial
estimation of the position is available. Then, the
beginning of the navigation could be a problem if
the robot is far from the route. To solve this
problem, a clustering approach has been used. The
robot makes small angular and linear movements
around the initial position, taking images during the
movement. Each image is localized comparing the
distance of its PCA components with the projections
in the database. Then, it is classified into the group
whose centre is closer to the localization of the
image. If this distance is over a threshold, the new
image will constitute a new cluster. Otherwise, it
will be included in the corresponding cluster and its
centre will be updated. Once all the images are
classified, the groups with few images are discarded
and the group in which the variance of the distance
of the elements is the lowest is chosen. The
corresponding location is calculated as the centre of
the chosen cluster. Fig. 6 shows this approach. In
this case, cluster 2 and position 9 would be selected.
PROBABILISTIC APPEARANCE-BASED NAVIGATION OF A MOBILE ROBOT - Controlling a Robot in Route
Following
395

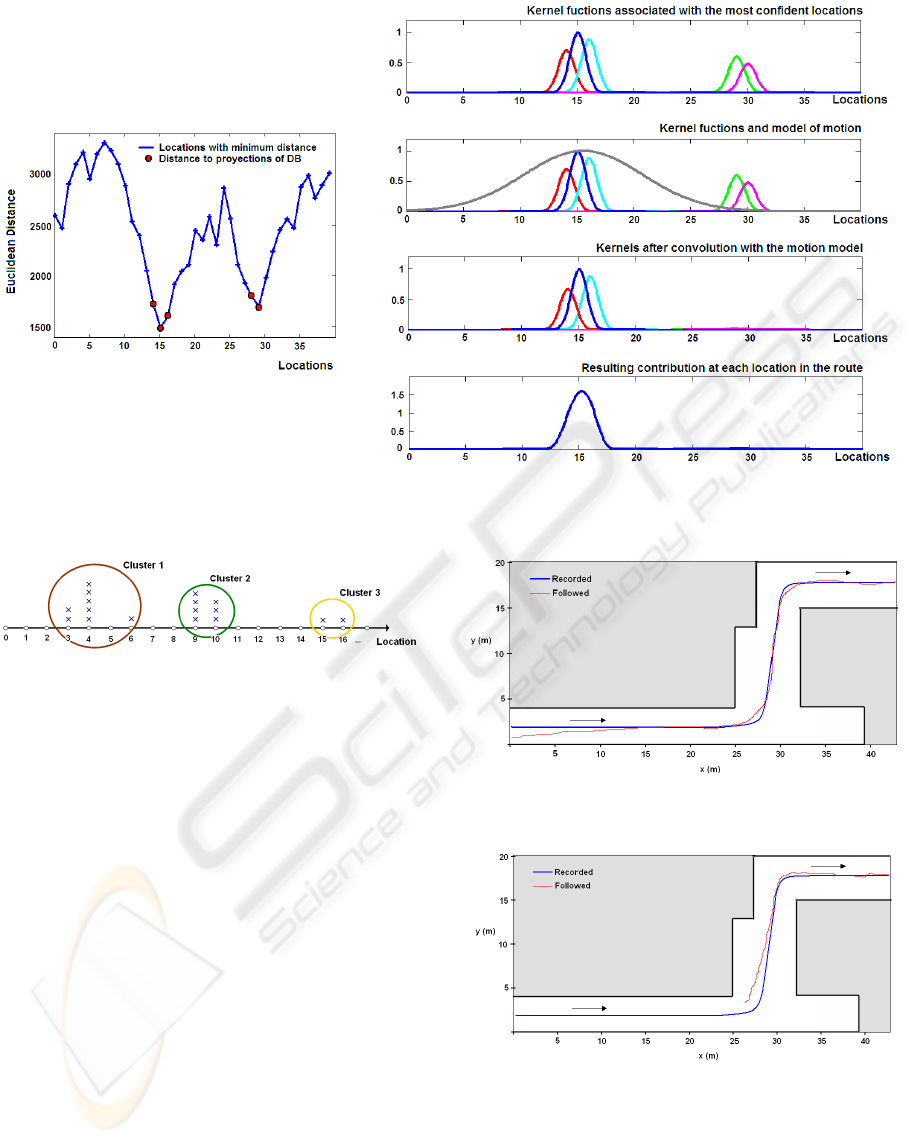
Figure 5: Improving localization through a probabilistic approach. In this case, after the process, it will be deducted that the
current position is the 15
th
one.
Figure 6: Clustering approach for initial localization of the
follower robot.
5 RESULTS
Several experiments have been carried out to
validate the approach. Fig. 7 and fig. 8 show a
typical route recorded in an office environment and
the route of the follower when it starts from two
different points around it. Typically, the follower
robot tends to the route and follows it, showing a
great performance on the straight lines and a
relatively bigger error in the turnings. However, with
this approach, the robot is able to find the route and
tend to it, showing a very stable behaviour till the
end. Comparing incremental PCA with batch PCA,
the batch one performs slightly better when
calculating overall error, but incremental PCA
performs correctly the task, as shown on fig. 7 and
fig. 8, and with the advantages it supposes. Fig. 9
shows the evolution of the localization during the
navigation of the follower robot and the probability
calculated, what can be a measure of the precision.
Figure 7: Results of navigation 1. Route recorded and
route followed.
Figure 8: Results of navigation 2. Route recorded and
route followed with a different initial point.
To carry out these experiments, two Pioneer P3-
AT robots have been used with two processors
onboard that communicate using a CORBA-based
architecture where they interchange the necessary
information. It is important to design an application
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
396

where the different robots can share the necessary
information in an easy and quick way due to the fact
that the follower robot has to use continuously the
database that the leader one is computing. An
additional processor has been added to the
architecture to carry out some calculations to reduce
the computational cost of the processes in the robots.
On fig. 9, the localization shows a correct
evolution, despite the visual aliasing effect in such
office environments, and the robot recovers correctly
of some errors in localization (such as those in
images 100 and 170). Also, the probability begins
with quite low value (the robot is far from the route).
Then, it tends to increase when the robot approaches
to the straight line and decreases again in the
turnings.
Figure 9: Localizations and final probability during
navigation with the route of the figure 7.
6 CONCLUSIONS
In this paper, an appearance-based multi-robot
following-route scheme is presented. The proposed
solution uses low resolution images from a
conventional video camera and PCA techniques to
extract the most relevant information along the
environment. To allow a new robot can follow the
route that another robot is recording at the same
time, an incremental PCA algorithm is employed.
The objective of the work is that other robots
can follow this route from a distance (as in space or
in time). To do it, a probabilistic algorithm has been
implemented to calculate their current position
among those that the leader has stored, and a
controller has been implemented, also based on the
appearance of the scenes, to calculate the linear and
turning speeds of the robot. Also, a clustering
method has been implemented to estimate the initial
position of the robot in a robust way.
Some experiments have been carried out with
two Pioneer 3-AT robots using a CORBA-based
architecture for communication. These experiments
show how the process employed allows following a
route in an accurate and robust way.
We are now working in other control methods
to reduce the error during the navigation, studying
the effects of illumination changes and occlusions
more accurately. Also, other techniques to compress
the information are being analysed to achieve a
higher speed of the follower robots. At last, more
complicated ways of building a map are being
evaluated so that the robot can find the route and
follow it although its initial position is far from this
route.
ACKNOWLEDGEMENTS
This work has been supported by MEC through
project DPI2007-61197 “Sistemas de percepción
visual móvil y cooperativo como soporte para la
realización de tareas con redes de robots”, and by
GV by the project GV/2007/292, “Modelos
estadísticos de imágenes naturales y de la corteza
visual primaria”, founded by Generalitat Valenciana.
REFERENCES
Artac, M., Jogan, M., Leonardis, A., 2002. Mobile Robot
Localization Using an Incremental Eigenspace Model.
In Proc. IEEE Int. Conf. on robotics and Automation,
pp. 1205-1030.
Balch, T., Arkin, R., 1998. Behavior-based formation
control for multi-robot teams. IEEE Transactions on
Robotics and Automation, 14(6), pp. 926-938.
Burschka, D., Hager, G., 2001. Vision-Based Control of
Mobile Robots. In Proc. IEEE Int. Conf. on Robotics
and Automation, pp. 1707-1713.
Fenwick, J., Newman, P., Leonard, J., 2002. Cooperative
Concurrent Mapping and Localization. In Proc. IEEE
Int. Conf. on Robotics and Automation,
pp. 1810-1817.
Ho, K., Newman, P., 2005. Multiple Map Intersection
Detection using Visual Appearance. In Proc. 3rd Int.
Conf. on Computational Intelligence, Robotics and
Autonomous Systems.
Kirby, M., 2001. Geometric data analysis, Wiley
Interscience.
Kröse, B., Bunschoten, R., Hagen, S., Terwijn, B., Vlassis,
N., 2004. Household robots: Look and learn. In IEEE
Robotics & Automation magazine, 11(4), pp. 45-52.
Maeda, S., Kuno, Y., Shirai, Y., 1997. Active navigation
vision based on eigenspace analysis. In Proc. IEEE
PROBABILISTIC APPEARANCE-BASED NAVIGATION OF A MOBILE ROBOT - Controlling a Robot in Route
Following
397

Int. Conf. on Intelligent Robots and Systems, Vol. 2,
pp. 1018-1023.
Matsumoto, Y., Ikeda, K., Inaba, M., Inoue, H., 1999.
Visual Navigation Using Omnidirectional View
Sequence. In Proc. IEEE Int. Conf. on Intelligent
Robots and Systems, pp. 317-322.
Payá, L., Reinoso, O., Gil, A., Pedrero, J., Ballesta, M.,
2007. Appearance-Based Multi-Robot Following
Routes Using Incremental PCA. In Int. Conf. on
Knowledge-Based and Intelligent Information and
Engineering Systems, pp. 1170-1178.
Thrun, S., 2002. Robotic Mapping: A Survey. Exploring
Artificial Intelligence in the New Milenium, Morgan
Kaufmann.
Turk, M., Pentland, A., 1991. Eigenfaces for recognition.
In Journal on Cognitive Neuroscience, 3(1), pp. 71-86.
Zhou, C., Wei, T., Tan, T., 2003. Mobile robot self-
localization based on global visual appearance
features. In Proc. of the 2003 IEEE Int. Conf. on
Robotics & Automation, pp. 1271-1276.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
398