LATTICE EXTRACTION BASED ON SYMMETRY ANALYSIS

Manuel Agust

ı-Melchor, Jose-Miguel Valiente-Gonz

alez and

Angel Rodas-Jord

Dept. de Inform

atica de Sistemas y Computadores, Universidad Polit

ecnica de Valencia

Camino de Vera s/n, Valencia, Spain

Keywords:

Lattice, grid, periodicity, wallpaper, regular pattern, symmetry, phase analysis.

Abstract:

In many computer tasks it is necessary to structurally describe the contents of images for further processing,

for example, in regular images produced in industrial processes such as textiles or ceramics. After reviewing

the different approaches found in the literature, this work redeﬁnes the problem of periodicity in terms of the

existence of local symmetries.

Phase symmetry analysis is chosen to obtain these symmetries because of its robustness when dealing with

image contrast and noise. Also, the multiresolution nature of the technique offers independence from using

ﬁxed thresholds to segment the image. Our adaptation of the original technique, based on lattice constraints,

has result in a parameter free algorithm for determining the lattice. It offers a signiﬁcant increase in computa-

tional speed with respect to the original proposal. Given that there is no set of images for assessing this type

of techniques, various sets of images have been used, and the results are apresented. A measure to enable the

evaluation of results is also introduced, so that each calculated lattice can be tagged with an index regarding its

correctness. The experiments show that using this statistic, good results are reported from image collections.

Possible applications of the lattice extraction are suggested.

1 INTRODUCTION

In many computer vision tasks a structural description

of the contents of images is needed for further pro-

cessing. This is the case of pattern and tiling images

obtained in industrial processes such as textile or ce-

ramics. These images are formed by the combination

of motifs that are regularly repeated using geometric

transformations to ﬁll the 2D plane without overlaps

or gaps. This plane tessellation forms a lattice or reg-

ular tiling which is a principal feature of these kind

of images. For this reason, lattice extraction is an im-

portant concern in tasks such as textile inspection, tile

cataloging, or QBIC (Query By Image Contents) ap-

plications.

We are interested in those wallpaper images that

are the most common expression of plane patterns.

These patterns are created following a strict set of

geometric rules that are described in the “Tiling and

Pattern Design Theory” (Horne, 2000). This the-

ory establishes that any planar design must include

two translational symmetries as well as other sym-

metries, such as rotations, reﬂections or glide reﬂec-

tions. It also establishes that there are only 17 combi-

nations or groups of these isometric transformations,

called Wallpaper Groups (Plane Symmetry Groups).

Therefore, the structural description of these designs

is composed of the translational symmetries (lattice),

the plane symmetry group they belong to, and the mo-

tif or fundamental domain used to create them.

In this work, we approach the ﬁrst problem: lat-

tice extraction. The wallpaper images always include

the translational symmetry, which means that the im-

age can be reconstructed by repeating the pattern, or

the motif, using two linearly independent unaligned

displacements. For this reason, lattice extraction can

be formulated as a problem of obtaining a grid of dis-

crete points that are related by being separated an in-

teger number of times by the length of the motif in

both directions. This grid is described, as is shown in

ﬁg. 1, by two direction vectors (four numerical val-

ues: two angles and two lengths). The parallelogram

formed by these vectors is called a Fundamental Par-

allelogram (FP) and, ideally, the image of this FP is

the motif originally used to create the pattern. But,

from the point of view of lattice extraction, the loca-

tion of the starting point of the grid does not matter.

Changing this point only changes the content of the

396

Agustí-Melchor M., Valiente-González J. and Rodas-Jordá Á. (2008).

LATTICE EXTRACTION BASED ON SYMMETRY ANALYSIS.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 396-402

DOI: 10.5220/0001085803960402

 SciTePress

FP, not the grid parameters. Wherever the grid is lo-

cated; the pattern can be rebuilt by repeating the FP

deﬁned at that point.

Figure 1: Grid computed from the detection of a repeated

area and characterized by two directional vectors.

For these reasons, lattice extraction is often for-

mulated in terms of ﬁnding periodicity in the image,

which takes us to the concept of grid previously enun-

ciated. Ideally, in synthetic images, it is possible to

compute, with complete accuracy, the repetitiveness.

The problem, in the case of real images, is due to the

existence of deﬁciencies that makes it impossible to

ﬁnd an exact match between pixel pairs and, there-

fore, the need to adjust automatically some tolerances

(differently in each image). Typical examples of deﬁ-

ciencies in textile or ceramic images are: noise or per-

spective distortion introduced in the process of image

acquisition; small variations in the industrial manu-

facturing process, or the variations inherent in hand-

made productions.

Several techniques have been employed to ap-

proach the 2D periodicity problem, as described in

detail in (O’Mara, 2002). The most common method

is autocorrelation. It is based in using part of the im-

age (typically one half) as a mask and performing

the autocorrelation of this mask with the whole im-

age. The peaks, or local maxima, of the autocorrela-

tion map can be extracted and the vectors that deﬁne

their unions used to propose a grid. Fig. 2 shows two

examples of autocorrelation maps on grey level im-

ages and the resulting grid superimposed on the im-

age from the point (0, 0). As may be noted, the sec-

ond case is wrong because the same threshold values

are used in both images and the correct tessellation is

not found. This example illustrates a common case of

autocorrelation failure. The threshold selection is an

image dependent problem, whereby images with low

dynamic range produce ﬂat autocorrelation maps and

it is therefore difﬁcult to ﬁnd signiﬁcant local max-

ima. In this work, we approach the problem in a dif-

ferent way. Instead of using the grey level values to

ﬁnd the repetitiveness between image points, we use

a symmetries space whose values depend on the local

symmetries in the neighborhood of each image point.

Because wallpaper images have strong inherent sym-

metries, the values in this new space peak clearly and

are less dependent on the image contrast and noise.

Figure 2: Autocorrelation results on grey level images.

Left: autocorrelation peaks. Right: grid obtained from con-

necting a ﬁxed number of peaks, as a ratio of the maximum.

The symmetries space is obtained through the

analysis of phase discrepancy (or congruency) be-

tween local frequency components at each image

point. These frequency components are computed at

several orientations and scales using wavelet ﬁlters.

This phase analysis enables the automatic detection

of these locally oriented symmetries and, therefore,

computes a high value of entropy, or symmetry, when

it estimates the orientation and scale corresponding

to the lengths or distances of appearing symmetries.

If more local symmetries appear at different orienta-

tions with the same periodicity value, then conﬁdence

in that value increases. In short, this process obtains

the periodicity of the signal from the identiﬁcation of

two local symmetries that repetitively appear in this

new space.

2 PHASE ANALYSIS

The chosen method of phase analysis was developed

by Kovesi (Kovesi, 1997). He established that im-

age features such as step edges, lines, roof edges and

match bands, all give rise to points where the Fourier

components of the image, computed at those points,

are maximally in phase. Oppositely, highly symmet-

ric image points will have minimally in phase fre-

quency components. Therefore, he introduces two

dimensionless quantities, called Phase Congruency

(PC) and Symmetry (Sym), which provide absolute

measurements of the signiﬁcance of these feature

points. The use of phase congruency for marking fea-

LATTICE EXTRACTION BASED ON SYMMETRY ANALYSIS

397

tures has signiﬁcant advantages over gradient based

methods. It is invariant to changes in image bright-

ness and contrast. Moreover it does not require any

prior recognition or segmentation of objects, thus en-

abling the use of universal thresholds values that can

be applied over a wide range of images.

Kovesi proposes a method to obtain these features,

based on the determination of the energy at a local

level. Kovesi’s method uses a multiresolution ap-

proach based on a pair of symmetric/antisymmetric

logGabor wavelet ﬁlters (M

, M

), from which an ac-

cumulated response for a given scale s and orientation

o is obtained using the eq. 1.

[e f

s,o

(x), o f

s,o

(x)] ← [I(x) ∗ M

s,o

, I(x)M

s,o

] (1)

The values e f

s,o

(x) (even) and o f

s,o

(x) (odd) can

be thought of as the real and imaginary parts of com-

plex valued frequency components. These values en-

able the content of a grey image to be rewritten as the

combination of a phase component (A

) and an orien-

tation component (φ) computed as follows:

s,o

(x) =

e f

s,o

(x) + o f

s,o

(x)

s,o

(x) = atan2(e f

s,o

(x) + o f

s,o

(x))

(2)

The Symmetry measurement is computed through

the eq. 3. It provides a value of local symmetry com-

bining the phase and orientation components obtained

from ﬁlter responses over multiple scales and orienta-

tions, Sym(x), as:

∑

o=1

∑

s=1

s,o

(x)[|cos(φ

(x)| − |sin(φ

(x)|] − T

∑

o=1

∑

s=1

s,o

(x) + ε

(3)

being φ(x) the overall mean phase angle, T

is a noise

compensation term that represents the expected re-

sponse from noise in the image (it is derived from the

computed values of A

∑

s=1

As, o), The ε is a small

constant to avoid ill-conditioned situations caused by

the very small values of the amplitude value A

s,o

. Eq.

3 can be rearranged as follow:

Sym(x) =

∑

o=1

∑

s=1

b[|e f

s,o

(x)| − |o f

s,o

(x)|] − T

∑

o=1

∑

s=1

s,o

(x) + ε

(4)

meaning that the symmetry value is the difference be-

tween the absolute responses of even-symmetric and

odd-symmetric wavelet ﬁlters. This measure varies

between [-1..+1] and is almost linear with phase devi-

ation. It must be noted that this model looks for image

transitions from white to black and in the reverse di-

rection. It can also be instructed to look for just one

transition by changing the term that involves the com-

bination of ﬁlter response. This is made by using a po-

larity parameter. Using the formulation for only one

transition (positive polarity) provides a wider range of

symmetry values, which facilitates the search for sim-

ilar values. Positive polarity is assumed in the rest of

the paper and the term −[e f

s,o

(x) − |o f

s,o

(x)|] is used

in the eq. 3. Thus, the Sym value ranges from [0.. +1].

a) b)

Figure 3: Kovesi’s phase analysis with polarity = +1: a)

original image, b) Symmetry values (equalized), and c) par-

tial 3D view of b).

Fig. 3 shows the results obtained applying eq. 4

over a grey level image (the luminance of the original

RGB image), with the default parameters proposed by

Kovesi. The motivation for making the transforma-

tion can be see in ﬁgure 3-c, where a detailed view of

the left part of the symmetry image is shown. It can

be seen that the transformation retains the repetitive-

ness and the spatial relationships of the original image

points, but it is now represented as peaks distributed

along the image in places where there is a high local

symmetry.

The phase analysis also produces, as a result, a

second component: the orientation component. This

reﬂects the orientation angle, for each image point,

for which the maximum symmetry value was reached.

We return to this component later.

3 LATTICE EXTRACTION

ALGORITHM

In this work we propose an methodology based on the

transformation from the bitmap space to a symmetry

domain where this search can be easily performed.

It is based on a three-stage algorithm to detect and

extract the grid of a regular image as follows: ﬁrst,

transform from the original RGB values of image do-

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

398

main into a symmetry domain (this is achived by us-

ing Kovesi’s symmetry model applied to a grey level

version of the original image); second, segmentation,

i.e. look for similar symmetry locations as identiﬁers

of equivalent local pixel contents; and third, detect

object unions by obtaining the direction vectors that

deﬁne the lattice by the studying the unions between

the identiﬁed observations.

The ﬁrst step is made through the use of the phase

analysis to obtain symmetry values. The phase anal-

ysis is ran over a grey scale version (I: the luminance

component) of the original RGB image. The analysis

is repeated over a negative version of the image (∼ I)

to be able to cope with an initially unknown distribu-

tion of original pixel values, dark backgrounds, and

clear motifs, or viceversa. This results in two symme-

try images SymD (direct) and SymI (inverse), together

with their corresponding orientation images.

Some decisions about the parameters of this trans-

formation must be taken. Firstly, the number of lev-

els of the multiresolution analysis depend on the im-

age resolution, and goes from 1 to log

(max(M, N)),

MxN being the image size. Secondly, the number of

orientations (O) is initially chosen as 180 (the com-

plete range of directions on the plane [0..π[) by using

increments of 1 degree. Rotational symmetries lower

that 30 degrees are not allowed in wallpaper designs,

so a 7 degree step in orientations can be used with

sufﬁcient accuracy - as the Nyquist theorem shows.

Finally, as the logGabor wavelet weighted by a

spread function is the ﬁlter used, the parameters of

both have to be chosen. For the wavelets, the cut-off

frequency value is computed from a minimum: the

minWaveLength value chosen as its related period can

be as much as the half the largest dimension of the

image, that is, to detect a minimum periodicity of 2 in

the image. For the spread that controls the sharpness

of the directional selectivity of the ﬁlters (as shown in

ﬁg. 4 ), the orientation is used together with a con-

stant (dThetaOnSigma = 1.7) value that ensures an

even coverage of the 2-D frequency spectrum. The

combined response of the ﬁlters for a constant value

of frequency and spread value, but different values of

orientation can be seen in ﬁg. 4.

At this point, the two versions (direct and inverse)

of the transformed domain of representation must be

examined and/or combined to obtain a binarized in-

termediate image - from which the last step can be

applied. This segmentation and direction determina-

tion needs a little more consideration if they are to be

achieved without imposing predetermined thresholds.

The subsections below discuss this topic.

Figure 4: From the left: ﬁlter appearance for a ﬁxed value of

frequency, orientation of 0 and spread values of 0.5, and 1.0,

and examples of ﬁlter directionality, for a spread of 1,77, a

constant frequency value and orientations of 60, and 180

degrees.

3.1 Segmentation Step: Looking for

Objects

At this point, the two versions (direct and inverse) of

the transformed domain of representation must be ex-

amined and/or combined to obtain a binarized inter-

mediate image - from which the last step can be ap-

plied.

This stage consist in analysing each one of the

symmetry images by looking for points that exhibit

the same maximum symmetry value. At least, three

are needed to establish two directions and, with them,

the resulting grid. But because we are working only

with the maximum values of the symmetry image, the

inﬂuence of noise is very marked. A more robust

strategy is possible by taking into account the neigh-

bourhood points of each local maximum because they

correspond to nearby points with high symmetry val-

ues.

To do this we perform a thresholding of the sym-

metry images with a iteratively decreasing threshold

value (T Sym) that is a percentage of the absolute max-

imum value. In each iteration, two binary images

(ob jectsD, ob jectI) are made showing “objects”, in

the sense of areas, around the local maxima that ap-

pear repeatedly and show certain shape regularity. A

simple labelling and comparison step enable us to ex-

tract these objects and obtaining the more frequently

repeated objects. A comparison measure between ob-

jects is taken as the euclidean distance between the

objects bounding boxes equalized and centered on the

mass center. As we do not know how much similar

the objects are, we use a threshold (T Similitude) that

is a percentage of the normalized euclidean distance.

This value is iteratively decreased until a minimum

number of similar objects is found. By putting this all

together we have the ﬁrst version of the segmentation

algorithm as:

function [objs,nObjs]<-extractObjs(symD,symI)

TSym <- 100%;

while (nObjs < 4) and (TSym > 0)

objectsD <- threshold( SymD, TSym )

objectsI <- threshold( SymI, TSym )

TSimilitude <- 100%;

while (nObjs < 4) and (TSimilitude > 0)

LATTICE EXTRACTION BASED ON SYMMETRY ANALYSIS

399

objs, nObjs<-count & compare (objectsD,

objectsI, TSimilitude)

if (nObjs < 4)

TSimilitude <- TSimilitude - 1;

endIf

endWhile

if (nObjs < 4)

TSym <- TSym - 1

endIf

endWhile

endFunction

The algorithm progress until a minimum number

of objects (three) are found, or until the T

Sym

range

has been exhausted. For simplicity, error checking

and convergence tests have not been included. Seg-

mentation in the symmetry domain was still difﬁcult

because of the existence of noise and strange values

obtained on the image border.

As an alternative, we studied the feasibility of the

orientation component that can be derived from the

phase analysis. We found that, in general, high values

in the symmetry domain were the result of the accu-

mulative contribution of ﬁlter responses over a wide

range of orientations. Furthermore, if we only look

in one orientation, a directly binarized version of the

orientation image can be obtained. In this image, a

value of 1 indicates that there was an “appreciable”

ﬁlter response in that direction, and a zero if not. The

decision about the appreciable ﬁlter response is based

on comparison with an estimation of the noise in each

image. These values are computed from the symme-

try value of the minimum analysis scale.

a) b)

Figure 5: Segmentation stage can be conducted over (a)

symmetry (equalized) or (b) orientation components.

We found that this binary orientation image re-

ﬂects the same objects as those found around the lo-

cal maxima in the symmetry space. Fig. 5 shows this

idea. In this work, we propose the use of this binary

orientation component because it is easier, than the

symmetry component, as thresholds do not have to be

established to segment objects. We propose a second

version of the segmentation algorithm as follows:

function [objs, nObjs]<-extractObjs(

orientacionD, orientacionI )

objectsD <- orientacionD

objectsI <- orientacionI

TSimilitude <- 100%;

while (nObjs < 4) and (TSimilitude > 0)

objs, nObjs<-count & compare (objectsD,

objectsI, TSimilitude)

if (nObjs < 4)

TSimilitude <- TSimilitude - 1;

endIf

endWhile

endFunction

3.2 Object Union Step

This point is devoted to the techniques that can be

used to establish the correct connection of the points

detected by the previous phase. They are focused on

the use of Hough and computational geometry tech-

niques. This is the same with any of the techniques

set forth in the introduction to solve the problem of

detecting periodicity.

Our proposal is to solve this stage in a three-step

ﬁltering function. Firstly, to be consistent with the

deﬁnition of periodicity of a signal, we will restrict

the list to the connections that are ”observable” be-

tween recurrences of the same object in the image.

Two elements are considered equal (ﬁg. 6-a)) if they

are similar in their characterization of “locally sym-

metrical”, i.e, the form of objects. This is the set of

possible directions.

a) b)

c) d)

Figure 6: Stages of the object union: (a) all possible con-

nections, (b) removing by grid restrictions, (c) voting re-

sults (number of votes for each orientation and displace-

ment pair), and (d) choosen directions.

Secondly, we reduce this connection list by using

the spatial constraints imposed by grid deﬁnition. Ac-

cordingly, a path between any of the grid points is

composed of a minimum number of minimum length

local connections. As described in (Mount, 2001),

this is the area of computational geometry. We use

the Relative Neighbourhood Graph (RNG) algorithm

over the established connections to obtain structurally

logical connections, because of its ability (Toussaint,

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

400

1980), to extract a perceptually meaningful structure

from a set of points. Finally, in a last step we use a

voting scheme for the selected connections to choose

the two most repeated (ﬁg. 6-c)). These two connec-

tions deﬁne the grid parameter (ﬁg. 6-d)) and they

they deﬁne the grid geometry (ﬁg. 6-d)) as shown onf

the next algorithm:

function [grid] <- vDirectors(objects, nObjs)

directionList <- tentativeGrid( objects )

directionList<-reduceConections( directionList )

v1,v2 <- vote( directionList )

grid <- (v1, v2)

endFunction

4 EXPERIMENTS

Once the lattice geometry has been extracted, a ﬁ-

nal step is needed in order to evaluate the cor-

rectness of the method. To achive this, correct

databases together with a comparison method must

be established. “Wallpaper Groups” (Joyce, 1997),

“Wikipedia Wallpaper Groups page” (Wikipedia,

2007), “Basic Tilings” (Savard, 2001), and “PSU

Near-Regular Texture Database” (Lee, 2001) contain

some image collections closely related to the ones in

our ﬁeld of application. An example of results ob-

tained with the ﬁrst of these databases is shown in ﬁg.

7. We have complemented the set by adding new im-

ages resulting from the application of a set of rigid

geometric transformations and different noise mod-

els in order to provide for wide range in the samples

available.

Figure 7: Results for some images (from left to right): orig-

inal image, established directions, and FP from image cen-

ter.

With respect to the comparison criteria, the lack

of uniformity and correct labeling of databases not

including grid geometry, makes expert intervention

sometimes necessary to evaluate the quality of the re-

sult. Nevertheless, an effort to deﬁne automatic cri-

teria based only on image parameters must be carried

out.

A ﬁrst approximation is to deﬁne the error in

terms of the euclidean distance between the origi-

nal and a reconstructed image replicating a selected

FP obtained using grid parameters. Thus we deﬁne,

for example, the Mean FP (MNFP) and Median FP

(MDFP) as the parallelogram obtained, respectively,

through the mean or median of image pixels related

to the grid geometry extracted. The choice of the

representative parallelogram is important for the ﬁ-

nal result of the reconstruction process, so it is not a

good statistical. Nevertheless, this method has sev-

eral problems: the selection of a representative FP

is needed, inﬂuencing the ﬁnal statistical results; the

image comparison process not only evaluates the cor-

rectness of grid geometry but also evaluates the image

content; and the lack of measure normalization.

To solve these problems we propose to calculate

a measure of Grid Adjust Error (GAE) to quantify

the error between the grid geometry computed and

the true image geometry. The formulation is done us-

ing a geometrical criteria intended to minimise errors

related to pixel distribution over the image, as char-

acterized by its variance S

, which can be expressed

as:

∑

i=1

∑

i=1

( ¯x

− ¯x)

(5)

Where the image has been divided in r sets of size

, mean ¯x

and variance S

, being n the size of the

image, n = n

+ n

+ ... + n

, and ¯x is the mean.

We use an image partition based on the computed

grid geometry and deﬁne the Variance FP (V FP) in a

similar way to (MNFP) and (NDFP) but using pixel

variance instead of mean or median. Thus the terms

in eq. 5 are instanced as S

= V FP

and ¯x

= MNFP

In such a way, when the geometry of the lattice is cor-

rectly determined, the ﬁrst term of equation tends to

zero and the second term to image variance. When

the computed geometry is incorrect, the opposite ef-

fect occurs. Both terms in eq. 5 range from 0 to S

Since we need to reduce image distribution ef-

fects, ﬁnally we propose the normalized measure of

GAE as follow:

GAE =

∑

i=1

V FP

0 6 GAE 6 1 (6)

Experiments with a number of 100 random lattices

were attempted on the wallpaper set, with the aim

of showing the statistical value tendency for wrong

lattices. The obtained variance values are between

553, 28 and 9804, 8, the statistic produced a mean

value of between 0, 945 and 1, 019, while the standard

deviation of the values is between 0, 008 and 0, 119.

The observed mean values over one are inherent in the

process of quantization: a result of the maths errors on

LATTICE EXTRACTION BASED ON SYMMETRY ANALYSIS

401

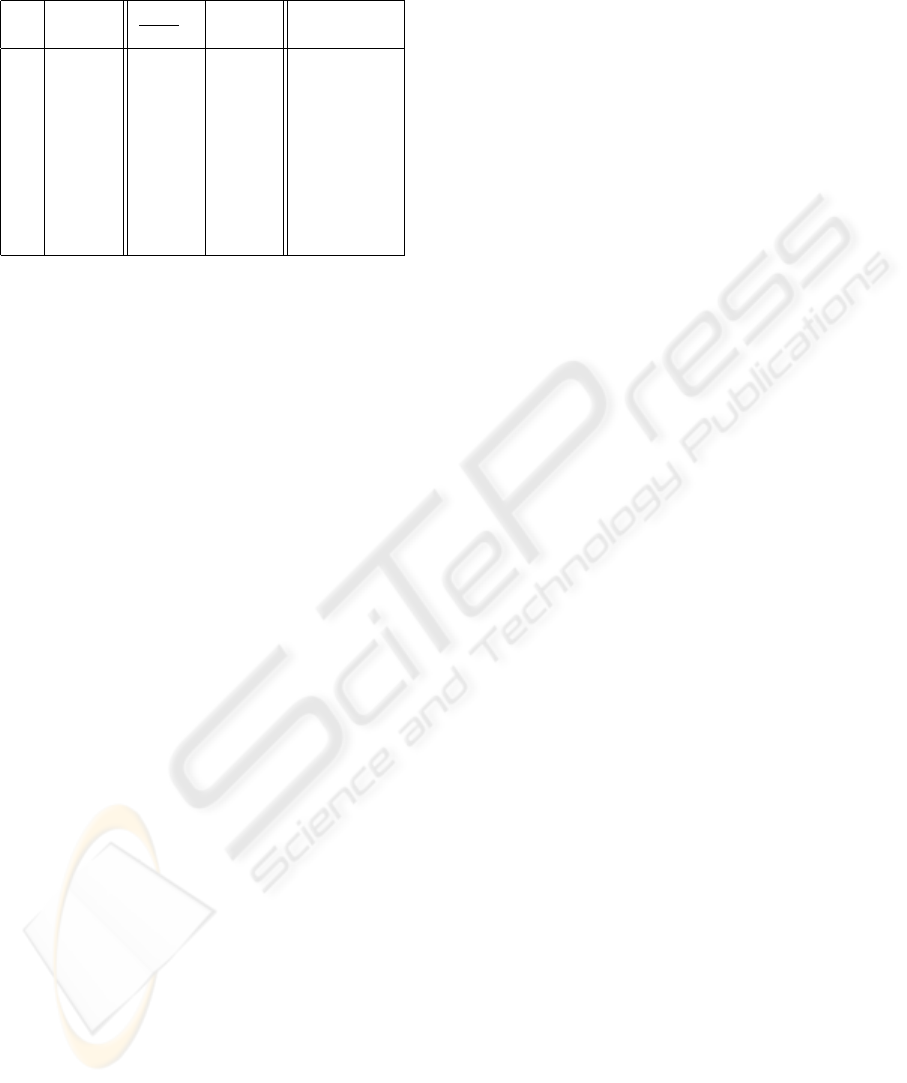
Table 1: Lattice evaluation for some images in Wallpaper

database.

GAE

nok

I S

V FP

GAE

[m, σ]

1 6070,0 529,7 0,09 [0,98, 0,08]

3 7564,4 1722,9 0,23 [0,94, 0,16]

4 6574,3 1581,7 0,24 [0,99, 0,04]

7 2538,3 619,3 0,24 [1,01, 0,02]

8 553,3 137,3 0,25 [1,00, 0,03]

9 7052,3 2258,6 0,32 [1,01, 0,07]

10 3218,9 946,7 0,29 [0,98, 0,19]

13 1115,6 380,5 0,34 [0,95, 0,17]

17 5511,6 2300,4 0,42 [0,95, 0,15]

rounding the values of the computed lattice geometry

to obtain pixel coordinates of the image.

Results for the “Wallpaper Groups” database are

shown in table 1. This table shows, from left to right,

image numbers and variance: the highness of this

value means that there is a greater dispersion on pixel

values; in regular images (as is the case) this means

there is noise. The next columns are the weighted

means of V FP and, the GAE values for the correct

grid extracted for the current image. Finally, a sta-

tistical distribution of GAE appears when using grids

extracted from the rest of the images, and this means

wrong lattice geometry values. From the last two

columns, as it was observed in the other collections,

the values of the statistical near to 0 identify a correct

lattice, meanwhile when this value is very near to 1

(the greatest deviation is 0, 19) can be concluded that

the lattice used does not offer a good reconstruction,

and it does not explain the image content.

5 CONCLUSIONS AND FUTURE

WORK

This work has shown an approach for extracting lat-

tice in regular image based on phase analysis. To

achive this goal we have revised the literature, and

observed the existing problems. The correspondence

between a formulation of lattice based on periodicity

versus symmetry, has led us to examine a multireso-

lution wavelet transform implementation. The study

of this, together with the justiﬁcation of how to cal-

culate the parameters of the proposed technique, has

resulted in an algorithms that produces a process that

can auto-adjust itself to the circumstances of each im-

age. A set of experiments was conducted on this al-

gorithm, and the results in the determination of the

lattice have been applied to different sets of images.

In addition, as products of this work, an statistic

is proposed to evaluate the correctness of the algo-

rithm. A methodology is also proposed that cover

all the variations an image may undergo, typically in

the context proposed for implementation. As lines of

future work we plan to explore: (a) the computation

of the rest of isometries that help us choose to which

Plane Symmetry Group an image belongs; (b) to ob-

tain a statistical conﬁrmation of the behaviour of the

GAE values for geometry values nearby to those of

the correct lattice; and (c) extract all the information

from the symmetry component, starting from the idea

that this aspect leads us to detect directly the axes of

reﬂection symmetry present in the image.

As a practical demonstration of the use of the al-

gorithms submitted, we are using this technique of de-

tecting repetitive patterns for real situations such as:

(a) obtaining a structural representation or syntactic of

the image that can be used for CBIR, and (b) rebuild-

ing, or recovering, the contents of an image, that has

been spoiled by noise, because stains, holes, breaks,

and other defects that involve the breakage or incom-

pleteness of the image.

ACKNOWLEDGEMENTS

This work is supported in part by project VISTAC

(DPI2007-66596-C02-01).

REFERENCES

Horne, C. E. (2000). Geometric symmetry in patterns and

tilings. Woodhead Publishing. ISBN 1 85573 492 3,

Abington Hall (England).

Joyce, D. E. (1997). Wallpaper groups (plane symmetry

groups). http://www.clarku.edu/ djoyce/.

Kovesi, P. (1997). Symmetry and asymmetry from local

phase. In AI’97, Tenth Australian Joint Conference on

Artiﬁcial Intelligence. pp 185-190.

Lee, S. (2001). Psu near-regular texture database.

http://vivid.cse.psu.edu/texturedb/gallery/.

Mount, D. (2001). Computational geometry: Proximity and

Location, cap. 63. CRC Press, 0-8493-8597-0.

O’Mara, D. (2002). Automated facial metrology, Chapter

4: Symmetry detection and measurement. PhD thesis,

University of Western Australia.

Savard, J. J. G. (2001). Basic tilings: The 17 wallpaper

groups. http://www.quadibloc.com/math/tilint.htm.

Toussaint, G. T. (1980). The relative neighbourhood graph

of a ﬁnite planar set. Pattern Recognition, vol. 12, pp.

261-268.

Wikipedia (2007). Wallpaper group — wikipedia, the free

encyclopedia. http://www.wikipedia.org/.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

402