RANDOM FOREST CLASSIFIERS FOR REAL-TIME OPTICAL

MARKERLESS TRACKING

Iñigo Barandiaran, Charlotte Cottez, Céline Paloc

VICOMTech, Mikeletegui Pasealekua 57, San Sebastian, Spain

Manuel Graña

University of Basque Country Computer Science School, Pº. Manuel de Lardizabal, 1 20009, San Sebastián, Spain

Keywords: Augmented Reality, Optical Tracking, Tracking by detection.

Abstract: Augmented reality (AR) is a very promising technology that can be applied in many areas such as

healthcare, broadcasting or manufacturing industries. One of the bottlenecks of such application is a robust

real-time optical markerless tracking strategy. In this paper we focus on the development of tracking by

detection for plane homography estimation. Feature or keypoint matching is a critical task in such approach.

We propose to apply machine learning techniques to solve this problem. We present an evaluation of an

optical tracking implementation based on Random Forest classifier. The implementation has been

successfully applied to indoor and outdoor augmented reality design review application.

1 INTRODUCTION

The main goal of the Augmented Reality (AR)

technology is to add computer-generated

information (2D/3D) to a real video sequence in

such a manner that the real and virtual objects

appear coexisting in the same world. In order to get

a good illusion, the registration problem must be

addressed. The real and virtual objects must be

properly aligned with respect to each other. In this

way, the position-orientation (pose) of the camera

respect to a reference frame must be accurately

estimated or updated over time. In this work, we

address the registration problem for interactive AR

applications, working on a fully mobile wearable

AR system based on a vision-based (optical) tracker.

Our approach to solve the registration problem

is based on the tracking of plane surfaces. Either in

an indoor or outdoor scenario, planes are common

structures. The ground, the building facades or walls

can be seen as planes. These 3D world planes and its

projection in the image are related by a homography.

Recovering this transformation it is possible to

estimate the position and orientation (pose) of the

camera.

Keypoint matching is the most important

feature of the markerless module. As described in

(Lepetit, 2006), we propose to treat wide line base-

line matching of features points as a classification

problem. We have implemented the Random Forest

classifiers and carried out an evaluation in the

context of optical markerless tracking for

Augmented Reality applications.

The article is structured as follows. Section 2

gives an overview of current optical tracking

techniques and methods in augmented reality

applications. Section 3 describes the approach to

keypoint matching based on Random Tree

classifiers. Section 4 presents a study of the

behaviour of the classifiers. In Section 5, a practical

augmented reality application using our

implementation is described. Section 6 summarizes

some conclusions and future work.

2 RELATED WORK

Though the real-time registration problem using

computer vision techniques has received a lot of

attention during last years is still far from being

solved. Ideally, an AR application should work

without the need to adapt neither the object nor the

environment to be tracked, by placing special

landmarks or references. This issue is known as

markerless tracking.

559

Barandiaran I., Cottez C., Paloc C. and Graña M. (2008).

RANDOM FOREST CLASSIFIERS FOR REAL-TIME OPTICAL MARKERLESS TRACKING.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 559-564

DOI: 10.5220/0001086405590564

 SciTePress

We can divide the optical markerless tracking

technologies in two main groups: recursive

techniques or model-based techniques. Recursive

techniques start the tracking process from an initial

guess or a rough estimation, and then refine or

update it over time. They are called recursive

because they use the previous estimation to

propagate or calculate the next estimation. During

the estimation process several errors may occur,

such as wrong point matching or ill conditioned data

that can degenerate the estimation. Due to the

recursive nature of this kind of tracking, they are

highly prone to error accumulation. The error

accumulation over time may induce a tracking

failure, requiring a new tracking process

initialization, which can be cumbersome and not

feasible in practical applications.

Other approaches are known as tracking by

detection or model-based tracking. In this kind of

techniques some information of the environment or

the object to be tracked is known a priori. They are

also known as model-based tracking because the

identification in the images of some features (texture

patches or corners) corresponding to a known model

are used to recognize such object. This kind of

tracking does not suffer from error accumulation

(drift) because, in general, does not rely on the past.

Furthermore, they are able to recover from a

tracking fail since they are based on a frame by

frame detection not depending on the past. They can

handle problems such as matching errors or partial

occlusion, being able to recover from tracking

failure without intervention (Williams, 2007).

Tracking by detection needs information data

about the object or objects to be tracked prior to the

tracking process itself. This data can be in the form

of a list of 3D edges (CAD model) (Vaccheti, 2004),

colour features, texture patches or point descriptors

(Lowe, 2001). A good comparison about different

point descriptors can be found in (Mikolajczyk,

2005). The tracker is trained with that a priori data,

to recognize the object from different points of view.

A good survey about different model-based tracking

approaches can be found in (Lepetit, 2005).

Some authors propose to use machine learning

techniques to solve the problem of wide baseline

keypoint matching (Özuysal, 2006). Supervised

classification system requires a previous process, in

which the system “is trained” with a determined set

of known examples (training set) that present

variations in all their independent variables. Once

the process is finished, the system is trained and

ready to classify new examples. The most widely

used supervised classifiers are for example, k-

Nearest Neighbours, Support Vector Machine or

decision trees.

While k-Nearest Neighbors or Support Vector

Machine can achieve good classification results,

they are still too slow and therefore not suitable for

real-time operation (Lepetit, 2004). Recently the

approach based on decision trees has been

successfully applied on tracking by detection during

feature point matching task (Özuysal, 2006).

Based on this recent progress in the field, we

propose to integrate Random Forest classifiers in the

implementation of a tracking module and carry out

some evaluation studies.

3 CLASSIFIER DESCRIPTION

In this section we describe a Random Forest

classifier implementation as a core of a tracking

module.

3.1 Random Trees

As in (Lepetit, 2006), we propose a supervised

classification method based on Random Forest for

interest point matching. The classifier is able to

detect key-point occurrences even in the presence of

image noise, variations in scale, orientation and

illumination changes. This classifier is a specific

variation of a decision tree (Breiman. 2001).

When the tree is constructed and trained it can

correctly classify a given data (example) by pushing

it down the tree. In order to do it, while the data is

descending down on the tree, in every node there is a

discriminant criteria which allows to know to which

child the example has to go.

A random tree is called random because instead

of do exhaustive search for the best combination of

features to be tested in each node to determine the

discriminant criteria, just some random

combinations of them are evaluated. When the

number of different classes to be recognized and the

size of the descriptor of such classes are high, an

exhaustive analysis is not feasible. In addition, the

examples that are going to be used during the

training process are selected at random from the

available ones. The combination of some random

trees forms a multi-classifier known as Random

Forest. One of the advantages of the Random Forest

is their combinational behaviour. Even when a

random tree can be weak by itself, their recognition

rate is low; the combination of such weak classifiers

can generate a strong one.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

560

3.2 Training

In supervised classification each class must be

defined before the training process itself. In order to

define the classes, we use a point extractor (Rosten,

2006) to get the candidate points and their

surrounding patches. Then the classifier assigns a

class number to each point, and their class descriptor

is defined. The descriptor of each class is

constructed as the intensity values of the pixels that

forms the extracted patch centered at interest point p.

Once the classes to be recognized by the classifier

are defined, the training set must be generated.

As described in (Lepetit, 2006) we can exploit

the assumption that the patches belong to a planar

surface; we can then synthesize different new views

of the patches using warping techniques as affine

deformations (Fig. 1). These affine transformations

are needed to allow the classifier to identify or

recognize the same class but seen from different

points of view and at different scales. This step is

particularly important for tracking, where the camera

will be freely moving around the object with six

degrees of freedom.

Figure 1: Randomly generated training examples of four

classes by applying affine transformations.

Once the training set is ready, the training task

can be performed. During this task, a number of

examples are randomly selected from the training

set. These examples are pushed down in the trees. In

order to decrease the correlation between trees, and

therefore increase the strength of the classifier,

different examples must be pushed down in each

tree. This randomness injection favours the

minimization of trees correlation.

The training step is needed in order to define

how each tree of the forest is going to test the

patches it receives, i.e, which pixels of the patch it

tests.

While building up the tree, each node of the

tree is treated as follows:

 N training examples from the training set are in

the node.

 S random sets of n pixels are selected.

 For each set, its information gain(Breiman,

2001) is calculated.

 The variable set with the greatest information

gain value is selected.

 The examples are tested with the selected set of

pixels. Depending on the result of this test,

they are pushed down to their corresponding

child node.

 The above process is recursively done for the

children nodes, whether until there is only one

example, or only one class is represented in

the remaining examples or the maximal

predefined depth is reached (Fig. 2).

The tests to be performed in each node are simple

comparison of the intensity values of the pixels

indicated by the pixels set. In case of a pixel set of

size two, the tests to be performed in each node

could be:

(

)

⎩

⎨

⎧

≥−

otherwiseldgoRightChi

tpvpvifdgoLeftChil

)()(

Where

)(

and

)(

represent the intensity values

of two pixels located at positions

p and

respectively. The values of the positions

p ,

were randomly selected during the training step. The

value of t represents a threshold that can be also

randomly selected while training.

Figure 2: Random Tree construction example.

Once the descriptors reach the bottom (maximal

depth) of the tree, it is said that they reached a leaf

node and the recursion stops. In leaf nodes the class

posterior distributions are stored. These distributions

represent the number of class examples from the

training set that has reached that node. Once an

example of a given class reaches a leaf node, the

posterior probability distribution stored in that node

must be updated accordingly.

3.3 Classification

Once the classifier is built, i.e, the pixels to be tested

in each node and the class posterior distributions are

calculated, it is ready to classify new examples

different from the ones in the training set. During the

RANDOM FOREST CLASSIFIERS FOR REAL-TIME OPTICAL MARKERLESS TRACKING

561

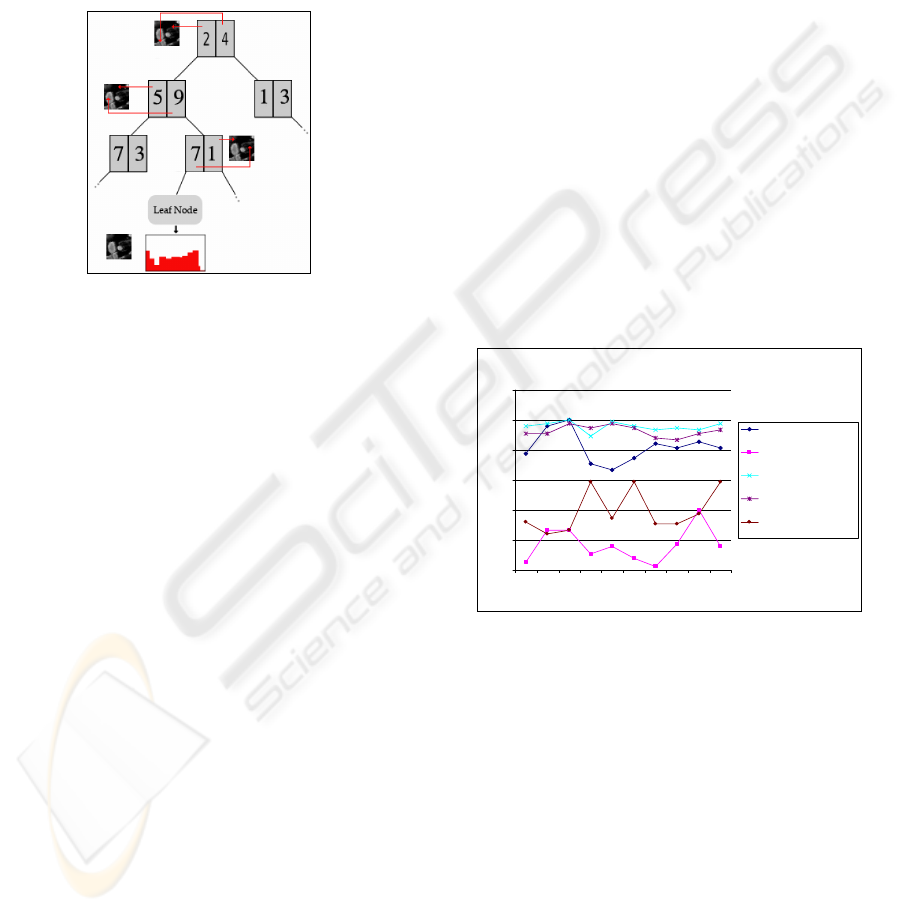
classification task any new example is dropped

down in every tree that constitutes the forest. These

examples will reach a leaf node depending on the

results of the tests obtained in the previous nodes

they visit (Fig. 3). The posterior distributions stored

in leaf nodes are used to assign a class probability

value to the examples that reach that

node,

()

=== nTTcYP

where

T is a

given tree of the forest and

is the reached node by

the example (patch) Y and

is the assigned class

label.

Figure 3: Example of image path classification.

As any multi-classifier, the random forest needs

to combine the independently generated output by

each tree in the forest, in order to assign a final class

label to the examples to be classified.

3.4 Tracking

As in (Lepetit, 2006) the Random Forest classifier

can be applied to interest point matching of a planar

surface prior to homography estimation (Hartley,

2004). After the classification step, wrong classified

patches (outliers) can be removed by using robust

estimation techniques such as RANSAC in order to

obtain a more accurate homography estimation.

Furthermore, the final estimation can be refined by

using Levenberg-Marquardt non-linear minimization

method starting from the estimation obtained by

RANSAC.

4 EVALUATION

We have implemented our own API to evaluate the

influence of different factors on the behaviour of

random forest classifiers during the training period

as well as during the execution period. Depending

on different factors such as, number of classes,

number of trees in the forest, or the size of the

training set, the point classification rate may vary. In

addition, other factors such as the training time and

the execution time are also very important factors to

be evaluated.

4.1 Combination Methods

During the run time point classification (point

matching) a probability and therefore a class label

must be assigned to every point (texture patch) that

needs to be matched against the model (trained

points). In this way, once the point extractor

generates the potential matches, they all must be

dropped down in the trees. Each tree will

independently give a probability value to a given

patch, and then all these values must be combined to

assign the most probable match. We have

implemented and evaluated the following

combination methods:

Our first study consisted in comparing the

classification rate of the respective methods. The

tests were done with the same number of trees and

with the same value of depth. Due to the random

behaviour of the random forest classifier, the tests

were run 10 times. All the tests were carried out with

100 different classes, 15 different trees, and 10 as

the maximum reachable depth. The results are

shown on the next figure.

Combination Methods

12345678910

Number of Test

%Good classification Rate

Maximal number of

Occurrences

Maximal Probability

Maximun of the Average of

probability

Maximun of the Product of

Probabilities

Ranking Method

Figure 4: Comparison between Combination Methods

performance.

As seen in Figure 4, the Maximum of the

average probability method reaches the best results,

being the most stable method amon

4.2 Classification Rate

We also evaluated the influence of the number of

trees on the classification rate. The results are shown

on the next figure. It is seen that reaching a certain

number of trees for a same training set, the increase

in performance is not significant (Fig. 5).

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

562

Recognition Rate

5 1015202530

Number of trees

% Good Classification Rate

Figure 5: Classification rate in function of the number of

trees.

4.3 Training Time

The training time was then evaluated. This factor

mainly depends on the size of the training set, this is,

on the number of examples that are going to be

dropped down in the trees to estimate the final

posterior probability distributions of each class. The

size of the training set has also impact on the

recognition rate, but no significant improvement of

classification rate are seen from about 500 training

examples, given the same forest, i.e, the same

number of trees with the same value of depth each

tree, while the training time notably increases. As in

the previous one, this test shows that the classifier

has an optimal maximum that once reached

(converged) the performance gain is very slow (Fig.

6).

Training Time

200

400

600

800

1000

1200

40 80 150 300 500

Number training examples

training time (s)

Figure 6: Training time in function of the size of the

training set.

4.4 Computational Cost

In order to evaluate the computational cost of the

method, we conducted some tests using different

hardware with the same memory amount but

different CPUs. Because of the highly CPU

demanding tasks during the tracking, the results

show clearly that the performance drastically

decreases with a poor hardware (Fig. 7).

CPU Type

Intel Core 2 DUO

1600Mhz

AMD 2100+ Mhz Intel Pentium 4

1300Mhz

Intel Centrino 1000

Mhz

Frames Per Second

Figure 7: Computational cost and CPU.

4.5 Discussion

The random tree classifier performs well when the

number of different points (classes) is moderate,

around 100 different points. When this number

increases, the classification rate starts to decrease.

This is because the strength of the trees decreases

individually due to the excessive number of different

classes, so that the classification ability or the forest

also decreases.

When the classification rate is low, the number

of miss-matched points (outliers) increases. Once

the population of outliers is high, the number of

iterations of either RANSAC or non-linear

estimation methods before convergence is very high.

5 APPLICATION

The approach described previously was applied

within an innovative system using head mounted

displays (HMD) for collaborative mobile mixed

reality design indoor and outdoor review.

Our tracking module uses natural features to

estimate the position and orientation of the camera,

mounted on the HMD. Once this transformation is

computed, the virtual object can be registered and

viewed through the HMD as part of the real world.

During the tracking process, the transformation must

be updated over time.

By using natural features, the use of artefacts

such as reflective markers is avoided, allowing the

system to be more flexible and being able to work in

non-well controlled conditions, such as outdoor

environments.

As described earlier, tracking by detection

techniques requires an off-line process where the

classifier is trained. During this period, one image of

a highly textured plane, such as a building facade or

a picture over a table, must be acquired. After the

acquisition, some features points and their

RANDOM FOREST CLASSIFIERS FOR REAL-TIME OPTICAL MARKERLESS TRACKING

563

surrounding texture patches are extracted from the

image (Rosten, 2006), and synthetic views of the

plane are generated.

Based on the results described previously, the

classifier is trained to be able to recognize about

100-130 different classes (points). The forest is

constructed with 15-20 trees, and a training set

compound of 500 synthetically generated examples,

in less than 30 minutes. This size of the training set

is a good compromise between training time and

final accuracy of the classifier. Training time is a

very important factor in practical situations such as

outdoor setup preparation time. Once the training set

is ready, the system is ready for tracking.

The obtained frame rate is about 20-25 frames

per second (near real-time) on a 1.6Ghz dual core

CPU. This frame rate may vary depending on the

accuracy of the tracker, i.e, depending on the

number of different points to be recognized. The

drift and jitter are well controlled, so no severe

movements of the objects occur. On a lower CPU,

such as the one installed on a JVC portable device,

the obtained frame rate is 5 frames per second, for

the same number of points.

In comparison with a recursive tracking

approach, the tracking by detection allows the

tracking to run faster and being more robust against

partial object occlusion, or fast camera movement.

The tracker can run indefinitely without requiring a

new initialisation.

6 CONCLUSION AND FUTURE

WORK

In this work we have presented an approach of

tracking by detection for plane homography

estimation using the Random Forest based classifier

for interest point matching. An evaluation and a

practical application of the approach in an

augmented reality setup has been described. The

proposed method is able to robustly track a plane

even if partial plane occlusion occurs, at real-time

frame rate.

We think that machine learning techniques such

as Random Forest is a very promising technique for

optical marker-less tracking.

We want to extend our work to support on-line

training classification (Özuysal, 2006). On-line

training allows the tracking to update the model with

new feature points not present in the original

training set. As described in (Williams, 2007) on-

line training can be exploited in several frameworks

such as Simultaneous Localization and Mapping

(SLAM).

Also the use of the new generation Graphic

Processor Units (GPU) to perform some task, such

as the generation of warping transformations during

training step is planned.

ACKNOWLEDGEMENTS

This work has been partially funded under the 6th

Framework Programme of the European Union

within the IST project “IMPROVE” (IST FP6-

004785, http://www.improve-eu.info/).

REFERENCES

Breiman, L., 2001. Random Forests. Machine Learning

Journal, Vol. 45, pages 5-32. ISSN 0885-6125

Hartley, R., Zisserman, A. 2004. Multiple View Geometry

in Computer Vision, Cambridge University Press, 2

edition. ISBN: 0521-54051-8.

Lepetit, V., Fua, P. 2006. Keypoint Recognition Using

Randomized Trees. IEEE Transactions on Pattern

Analysis and Machine Intelligence, Vol. 28(9), pages

1465-1479. ISSN: 0162-8828.

Lepetit, V., Fua, P. 2005. Monocular model-based 3D

object tracking of rigid objects: A survey. Foundations

and Trends® in Computer Graphics and Vision., Vol.

1, pages 1–89.

Lepetit, V., Pilet, J., Fua, P. 2004. Point Matching as a

Classification Problem for Fast and Robust Object

Pose Estimation. In Conference on Computer Vision

and Pattern Recognition. ISBN: 0-7695-2158-4.

Lowe, D. 2004. Distinctive Image Features from Scale

Invariants Keypoints. International Journal of

Computer Vision. Vol. 20(2), Pages 91-110.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman,

A., Matas, J., Schaffalitzky, F., Kadir, T., and Gool, L.

V. 2005. A Comparison of Affine Region Detectors.

Int. Journal of Computer Vision. Vol. 65(1-2), pages

43-72. ISSN:0920-5691.

Özuysal, M., Fua, P., Lepetit, V. 2006. Feature Harvesting

for Tracking-By-Detection. In Proc. European

Conference on Computer Vision, pages 592-605.

ISBN:3-540-33836-5.

Rosten, E., Drummond, T. 2006. Machine Learning for

High-Speed Corner Detection. In Proc. European

Conference on Computer Vision. Pages 430- 443.

ISBN 3540338322.

Vacchetti, L., Lepetit, V., Fua, P. 2004. Combining Edge

and Texture Information for Real-Time Accurate 3D

Camera Tracking. In Proc. IEEE and AM International

Symposium on Mixed and Augmented Reality. Vol. 4,

pages 48-57. ISBN:0-7695-2191-6.

Williams, B., Klein, G., Reid, I. 2007. Real-time SLAM

Relocalisation. In Proc. IEEE Interrnational

Conference on Computer Vision.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

564