RECOGNITION OF TEXT WITH KNOWN GEOMETRIC AND
GR
AMMATICAL STRUCTURE
Jan Rathousk´y
Department of Control Engineering, Faculty of Elec. Eng., Czech Technical University in Prague, Czech
Martin Urban
Eyedea Recognition, Prague, Czech Republic
Center for Applied Cybernetics, Faculty of Elec. Eng., Czech Technical University in Prague, Czech
Vojtˇech Franc
Fraunhofer Institut FIRST IDA, Berlin, Germany
Keywords:
Text Recognition, Sructured Support Vector Machines, License Plate Recognition.
Abstract:
The optical character recognition (OCR) module is a fundamental part of each automated text processing sys-
tem. The OCR module translates an input image with a text line into a string of symbols. In many applications
(e.g. license plate recognition) the text has some a priori known geometric and grammatical structure. This
article proposes an OCR method exploiting this knowledge which restricts the set of possible strings to a
limited set of feasible combinations. The recognition task is formulated as maximization of a similarity func-
tion which uses character templates as reference. These templates are estimated by a support vector machine
method from a set of examples. In contrast to the common approach, the proposed method performs character
segmentation and recognition simultaneously. The method was successfully evaluated in a car license plate
recognition system.
1 INTRODUCTION
Recognition of text in images is an important part of
the pattern recognition field. Systems for text recog-
nition are generally referred to as OCR (Optical Char-
acter Recognition) systems.
This article presents a method for OCR that makes
use of the fact that many examined texts have a given
structure that can be described by a common model.
In other words, the text yields to some grammar and
layout, determining the number of symbols, their rel-
ative width and position and also the kind of sym-
bols that can appear in each position. The advantage
of this approach is that using the a priori knowledge
about the text structure reduces the number of pos-
sible configurations, thus improving the success rate
of the method, especially when the input image is in
a bad quality. Typically the method fits for recogni-
tion of short structured texts (see Figure 1) taken in
low resolution and possibly inappropriate light condi-
tions.
The text recognition itself consists of two sub-
(a) license plate
(b) license plate (c) ADR/RID plate
F
igure 1: Examples of images with short structured texts
with a priori known geometrical and grammatical structure.
tasks – the text segmentation, where areas (segments)
of the image containing single characters are found
and the text recognition, where the characters in in-
dividual segments are determined. The classical ap-
proach is to perform these subtasks separately, which
leads to recognition errors if the segmentation is
done incorrectly. Systems using this approach have
194
Rathouský J., Urban M. and Franc V. (2008).
RECOGNITION OF TEXT WITH KNOWN GEOMETRIC AND GRAMMATICAL STRUCTURE.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 194-199
DOI: 10.5220/0001086501940199
Copyright
c
 SciTePress

been proposed for example in (Shapiro and Gluhchev,
2004; Ko and Kim, 2003; Lee et al., 2004) or (Rah-
man et al., 2003). A different approach, used also
in the proposed method is to perform both operations
at once, thus treating the text not as a sequence of
individual characters, but rather as one line of text
that is processed as a whole. A method for printed
text recognition using this approach is described in
(LeCun et al., 1998; Savchynskyy and Kamotskyy,
2006).
In our approach, the classifier is defined by a text
structure (i.e. a grammar and a layout) and by a vector
of parameters, representing the optimal appearance
of individual characters. The method is based on a
linear classifier. The classifier parameters are opti-
mized according to a training set of examples using
the structured support vector machine (SVM) learn-
ing method.
The next section describes how the text structure
is modeled and sections 3 and 4 are focused on the
learning and classification task. Finally we present
experiments that were performed on car license plate
and ADR/RID images.
2 TEXT STRUCTURE
MODELLING
A digitized greyscale image I is a H ×W matrix, ele-
ments of which are the intensity values of correspond-
ing pixels. A segment of width ω ∈ N of the image I is
a submatrix of I formed by ω succesive columns. The
left border λ of the segment is the index of the left-
most column of the segment (the lowest index). Each
segment can be fully described by a pair (λ, ω) and
also each pair (λ, ω) ∈ N
2
, λ + ω ≤ W + 1 defines a
segment in I. We will denote a segment of I with left
border λ and width ω as I[λ, ω]. The element in the
i-th row and j-th column of I will be denoted I
ij
and
I
ij
[λ, ω] for the segment I[λ, ω].
It is assumed that the input image depicts the text
in a horizontal position and that the top and bottom
edge of the image coincides with the top and bottom
of the text. Neither the left-to-right position nor the
width of the text is known, these are considered as
unknown parameters, which makes it possible to cope
with an imprecise detection of the left and right text
border.
The text structure is described by a geometric
model. A model µ is given by a sequence of seg-
ments the text contains. Each segment is described
by its left border λ (i.e. its position), width ω and a
type identifier. The type identifier is a subset of al-
phabet A containing all characters possibly appearing
in a given segment. Thus the model has the form of
a 3× N
µ
table, where N
µ
is the number of segments.
Figure 2 shows a typical model of a license plate text.
The spaces between characters are modelled by a se-
quence of special space segments of width equal to
one. On the other hand, the rest of the image that is
not covered by the model is omitted.
o
s
ω
λ
1
1
N
L
N
NNNN
µ
Figure 2: Typical structured text model. N stands for a type
identifier denoting numbers, L means letters and empty nar-
row segments contain only space characters.
Because the width of the text in the image is un-
known and the width of the model is fixed, it is nec-
essary to find the ratio between the two. This ratio is
called scale. The next unknown parameter is the left-
to-right position of the text which is described by the
index of its leftmost column called offset.
The combination of a model µ, scale s and offset
o determines the geometry of the text and the model
also defines all possible strings. The string will be de-
noted Σ and thus the complete description of a given
image consists of four parameters – µ, s, o and Σ. We
will also denote I
s
the image I that has been resized
by scale s to dimensions
1
H × ⌈W · s⌉.
3 STRUCTURED SVM
Classification is a process that assigns a state from a
given set of all possible states to an object, based on
some observation made on the object. Classifier (or
classification strategy) is a function f : X → Y that
assigns to each observation x ∈ X a state y ∈ Y. Next
let us define a loss function ∆ :Y ×Y → R that assigns
to each pair (y, f(x)) a real number loss expressing
the penalty for classifying x into f(x), while the real
state is y. We assume that ∆(y, y
′
) = 0 if y = y
′
and
∆(y, y
′
) > 0 if y 6= y
′
.
The structured support vector machine learning
method is based on finding an optimal classification
strategy that minimizes the empirical risk defined as
R
emp
( f) =
1
m
m
∑
k=1
∆(y
k
, f(x
k
)), (1)
1
The ⌈·⌉ denotes the nearest integer towards infinity –
ceiling.
RECOGNITION OF TEXTWITH KNOWN GEOMETRIC AND GRAMMATICAL STRUCTURE
195

and maximizes the margin supposing that there is a
set of example data {(x
1
, y
1
), . . . , (x
m
, y
m
)} available
(Vapnik, 1998). Here y
k
denotes the true state of x
k
.
To choose the optimal decision strategy, it is first
necessary to determine the set of functions from
which the optimal function should be chosen. Usually
a set of functions is described by a function F(w;x, y)
dependent on some vector of parameters w. Then the
decision strategy has the form of
ˆy = f(w;x) = argmax
y∈Y
F(w;x, y) (2)
and choosing the optimal strategy means choosing the
optimal parameter vector w.
If a classifier is linear in the vector of its param-
eters, the optimal vector of parameters can be found
using the structured support vector machine (SVM)
learning algorithm. There are two main differences
between classical and structured SVM. First, struc-
tured SVM allows for much more complicated output
spaces than classical SVM, where the output space
is merely a set of class labels. Second, arbitrary
loss functions may be used, satisfying only previously
mentioned conditions.
A classifier linear in the vector of its parameters w
can be expressed as an inner product of the vector w
and some vector function Ψ(x, y) of the observation x
and state y. This means that (2) takes the form of
ˆy = f(w;x) = argmax
y∈Y
hw, Ψ(x, y)i. (3)
In the case described in this article, the state y is
defined by a combination of four parameters – scale s,
offset o, model µ and string Σ – introduced in section
2. Observation x corresponds to the input image I.
Substituting these in (3) we can write
( ˆs, ˆµ, ˆo,
ˆ
Σ) = argmax
s,µ,o,Σ
hw, Ψ(I, (s, o, µ, Σ))i. (4)
The vector w represents prototypes of all charac-
ters a of the alphabet A. Prototypes E(a) are images
that all have the same height H as the input image.
Vector w is created by placing these images column-
wise after each other in a given order. The inner prod-
uct hw, Ψ(I, (s, o,µ, Σ))i expresses a similarity func-
tion of input image I resized by scale s and an im-
age created from prototypes of characters in string Σ
placed according to the model µ and offset o. We use
the general form of the similarity function suggested
in (Savchynskyy and Kamotskyy, 2006)
hw, Ψ(I, (s, o, µ, Σ))i =
N
µ
∑
i=1
(E(a
i
) ⊙ I
s
[o+ λ
i
, ω
i
]),
(5)
where Σ = (a
1
, . . . , a
N
µ
) is a string, E(a
i
) is the pro-
totype of the character a
i
and the ⊙ operator denotes
the similarity function between the prototype and the
segment I
s
[o + λ
i
, ω
i
]. We use the cross correlation
function for this purpose as described in (Franc and
Hlav´aˇc, 2006)
E(a
i
) ⊙ I
s
[o+ λ
i
, ω
i
] =
H
∑
j=1
ω
i
∑
k=1
E(a
i
)
jk
I
s
jk
[o+ λ
i
, ω
i
],
(6)
The mapping function Ψ is thus defined implicitly by
the equations (5) and (6).
The vector Ψ(I, (s, o, µ, Σ)) can also be con-
structed explicitly by placing the segment I
s
[o +
λ
i
, ω
i
] to the vector Ψ in the same way as the pro-
totype E(a
i
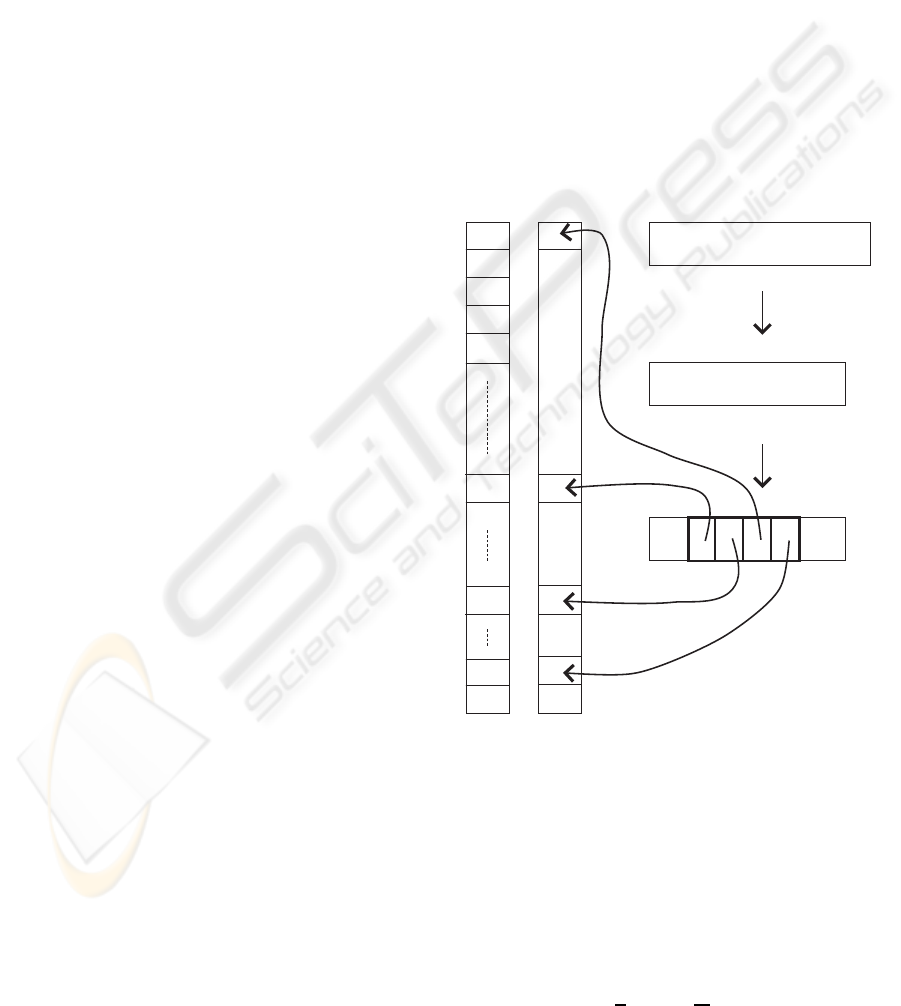
) is placed in the vector w (figure 3). The
remaining elements of Ψ are set to zero so that these
do not influence the value of (5).
A
B
C
D
E
T
0
8
9
I
I
s
s
Σ = "T0A8"
µ, o
w
Ψ
o
resize
Figure 3: An example of construction of vector Ψ from im-
age I. First, I is resized to I
s
, second a model µ is placed on
I
s
on position o and finally segments are placed into Ψ on
positions corresponding to characters in Σ.
Finding the optimal vector of parameters w in
the sense of minimization of the empirical risk (1)
and maximization of the margin is a QP optimization
problem in the following form
min
w
1
2
||w||
2
+
C
m
m
∑
k=1
ξ
k
(7)
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
196

such that
∀k = 1, . . . , m, ∀y ∈ Y :
hw, Ψ(x
k
, y
k
) − Ψ(x
k
, y)i ≥ ∆(y, y
k
) − ξ
k
, (8)
where ξ
k
are so called slack variables and C is a con-
stant expressing the trade off between margin max-
imization and empirical risk minimization (Vapnik,
1998). Due to the large number of constraints (8),
the QP task is performed iteratively. Most violated
constraints are added to the working set in each it-
eration. Finding these constraints requires that there
exists an algorithm for solving the so called loss aug-
mented classification task
ˆy = argmax
y∈Y
(∆(y, y
k
) + hw, Ψ(x
k
, y)i). (9)
The maximum in (9) is searched over all y ∈ Y. Since
y is given by the parameters (s, µ,o, Σ), the geometric
models are also used in the optimization (learning)
process.
The correct segmentation of all images in the
training sets is known and it is given by the states
y
k
. Thus each column of the training image can be
labeled according to the character it depicts. The loss
function ∆(y, y
k
) was defined as the number of incor-
rectly labeled image columns for segmentation based
y.
A general algorithm solving the problem (7) is
described in (Tsochantaridis et al., 2005) and needs
an external QP solver. A modified algorithm used in
this work is described in detail in (Franc and Hlav´aˇc,
2006).
4 CLASSIFICATION TASK
EVALUATION
The recognition algorithm implements the maximiza-
tion of (5) over all variables, i.e.
( ˆs, ˆµ, ˆo,
ˆ
Σ) = argmax
s,µ,o,Σ
hw, Ψ(I, (s, o, µ, Σ))i =
= argmax
s,µ,o,Σ
∑
N
µ
i=1
(E(a
i
) ⊙ I
s
[o+ λ
i
, ω
i
]). (10)
Since the model assumes that characters in different
segments are independent of each other, the similar-
ity function can be maximized within each segment
separately.
( ˆs, ˆµ, ˆo,
ˆ
Σ) =
= argmax
s,µ,o
N
µ
∑
i=1
max
a
i
(E(a
i
) ⊙ I
s
[o+ λ
i
, ω
i
]). (11)
The algorithm based on equation (11) is shown in
figure 4.
Input:
Image I of height H and width W
A set of models M
Prototypes E(a) for all symbols a
Set of scales S and set of offsets O
Output:
Scale ˆs, offset ˆo, model ˆµ and string
ˆ
Σ = ( ˆa
1
, . . . , ˆa
n
)
maximizing the similarity function.
begin
TOTALMAX := −∞
forall s ∈ S do
I
s
= resize(I, s)
forall µ ∈ M do
forall o ∈ O do
VALUE := 0
Initialize array CHAR of length N
µ
for i = 1 to N
µ
do
MAXC := −∞
foreach a
i
do
C := E(a
i
) ⊙ I
s
[o+ λ
i
, ω
i
]
if C > MAXC then
MAXC := C
CHAR[i] := a
i
end
end
VALUE := VALUE+ MAXC
end
if VALUE > TOTALMAX then
TOTALMAX := VALUE
ˆµ := µ ˆo := o ˆs := s
b
Σ := CHAR
end
end
end
end
end
Figure 4: Basic algorithm for similarity function maximiza-
tion.
5 EXPERIMENTS
In this paper we present experiments on three data
sets. The first data set consists of car license plates
from four European countries (Czech, Hungarian,
Slovak and Polish). The second data set contains
Saudi-Arabianlicense plates and the third set contains
ADR/RID plates.
The first set consists of 2121 training images and
521 testing images. The input image size was 13x200
pixels. Eight models in total were used to describe
the geometry and the syntax of the strings in the set.
The recognized alphabet consists of 39 symbols. Al-
though distinct text fonts appear in the set, just one
prototype per character from the alphabet was used.
The second data set with Saudi-Arabian license
plates consists of 627 training examples and 157 test-
ing examples. Only one geometrical model with the
RECOGNITION OF TEXTWITH KNOWN GEOMETRIC AND GRAMMATICAL STRUCTURE
197

7 S 2 1 2 5 7
F L X − 1 1 0
D W 0 3 3 4 J
B R − 5 4 0 A U
Figure 4: Four examples of input images from the first data
set with recovered segmentation and recognized strings.
     
Figure 5: An example of Saudi-Arabian license plate image
with recovered segmentation.
3 3
1 2 1 9
Figure 6: An example of a top and a bottom line from ADR
plate with recovered segmentation and recognized strings.
alphabet of 27 symbols was used. The input image
size was 24x100 pixels.
The third data set contains two-line ADR/RID
plates. The set consists of 109 training and only 20
testing images. Each text line was recognized inde-
pendently. The image resolution of the ipnut line was
13x140 pixels.
Severalexamplesof input images and OCR results
are shown in Figure 4, Figure 5 and Figure 6.
The total error rates achieved by the algorithm on
the testing sets are given in Table 1, Table 2 and Ta-
ble 3. Most of the errors are due to character mis-
classification. The segmentation error is typically low
in this approach. If necessary, the total error can be
reduced joining a nonlinear character classification
module which cuts down the character misclassifica-
tion error.
In general, the error rate depends on the quality of
the input image sets and the complexity of the given
recognition task (i.e. the number of all possible solu-
tions). Unfortunately we did not find any public refer-
ence data set to enable the objective evaluation of the
Table 1: Error rates on data set consisting of Czech, Hun-
garian, Polish and Slovak license plates.
algorithm total segmentation character
error error misclsf
reference alg. 10.1% 3.3% 6.8%
proposed alg. 4.6% 0.95% 3.6%
Table 2: Error rates on Saudi-Arabian license plates.
algorithm total segmentation character
error error misclsf
reference alg. 18.1% 6.8 % 11.3%
proposed alg. 9.7 % 2.3 % 7.4%
Table 3: Error rates on ADR/RID plates.
algorithm total segmentation character
error error misclsf
reference alg. 5% 5% 0.0%
proposed alg. 0.0% 0.0% 0.0%
presented algorithm.
Therefore we took as a reference another algo-
rithm described in (Franc and Hlav´aˇc, 2006). This
reference algorithm is also based on structured SVM,
however it does not make use of any geometrical or
syntax model.
6 CONCLUSIONS
In this article we proposed an OCR algorithm for
structured texts that is based on exploiting the knowl-
edge about their geometricand grammatical structure.
We introduced a formal description of a large vari-
ety of structured texts in terms of a geometric model.
We also formulated the classification task in terms of
maximizing a similarity function based on (Savchyn-
skyy and Kamotskyy, 2006; Franc and Hlav´aˇc, 2006)
that compares the input image to an idealized one for
all possible configurations. The idealized image con-
sists of prototypes of individual characters. These
prototypes are interpreted as parameters of the clas-
sifier that are to be determined by learning. We used
the SVM method for structured classifiers described
in (Franc and Hlav´aˇc, 2006).
The described OCR method was tested in many
experiments and currently was proved as a part of
a commercial license plate recognition system. The
algorithm fits especially for low quality images of
strings with limited number of geometric and gram-
matical models.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
198

ACKNOWLEDGEMENTS
This work has been sponsored by The Czech Min-
istry of Education project 1M0567 (M.U.) and by
The Czech Science Foundation project 201/06/1821
(J.R.). The third author (V.F.) was supportedby Marie
Curie Intra-European Fellowship grant SCOLES
MEIF-CT-2006-042107.
REFERENCES
Franc, V. and Hlav´aˇc, V. (2006). A novel algorithm for
learning support vector machines with structured out-
put spaces. Research Report K333–22/06, CTU–
CMP–2006–04, Department of Cybernetics, Faculty
of Electrical Engineering Czech Technical University,
Prague, Czech Republic.
Ko, M.-A. and Kim, Y.-M. (2003). License plate surveil-
lance system using weighted template matching. In
Proceedings of the 32nd Applied Imagery Pattern
Recognition Workshop (AIPR’03). IEEE Computer
Society.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).
Gradient-based learning applied to document recogni-
tion. Proceedings of the IEEE, 86(11):2278–2324.
Lee, H.-J., Chen, S.-Y., and Wang, S.-Z. (2004). Extrac-
tion and recognition of license plates of motorcycles
and vehicles on highways. In Proceedings of the
17th International Conference on Pattern Recognition
(ICPR’04). IEEE Computer Society.
Rahman, C. A., Badawy, W., and Radmanesh, A. (2003).
A real time vehicle’s license plate recognition system.
In Proceedings of the IEEE Conference on Advanced
Video and Signal Based Surveillance (AVSS’03). IEEE
Computer Society.
Savchynskyy, B. and Kamotskyy, O. (2006). Character tem-
plates learning for textual image recognition as an ex-
ample of learning in structural recognition. In Pro-
ceedings of the Second International Conference on
Document Image Analysis for Libraries (DIAL’06),
pages 88–95. IEEE Computer Society.
Shapiro, V. and Gluhchev, G. (2004). Multinational license
plate recognition system: Segmentation and classifi-
cation. In Proceedings of the 17th International Con-
ference on Pattern Recognition, volume 4, pages 352–
355.
Tsochantaridis, I., Joachims, T., Hofmann, T., and Altun,
Y. (2005). Large margin methods for structured and
interdependent output variables. Journal of Machine
Learning Research, 6:1453–1484.
Vapnik, V. (1998). Statistical Learning Theory. John Wiley
& Sons, Inc.
RECOGNITION OF TEXTWITH KNOWN GEOMETRIC AND GRAMMATICAL STRUCTURE
199