CAMERA MOTION ESTIMATION USING PARTICLE FILTERS

Symeon Nikitidis, Stefanos Zafeiriou and Ioannis Pitas

Aristotle University of Thessaloniki, Department of Informatics, Box 451, 54124 Thessaloniki, Greece

Keywords:

Camera Motion Estimation, Vector Field Model, Particle Filtering, Expectation Maximization Algorithm.

Abstract:

In this paper a novel algorithm for estimating the parametric form of the camera motion is proposed. A novel

stochastic vector ﬁeld model is presented which can handle smooth motion patterns derived from long periods

of stable camera movement and also can cope with rapid motion changes and periods where camera remains

still. A set of rules for robust and online updating of the model parameters is also proposed, based on the

Expectation Maximization algorithm. Finally, we ﬁt this model in a particle ﬁlters framework, in order to

predict the future camera motion based on current and prior knowledge.

1 INTRODUCTION

Video, in contrary with image, possesses valuable

information since it extends spatial information and

records the evolution of events over time. This dy-

namic property, has been extensively investigated by

the scientiﬁc community for semantic characteriza-

tion and discrimination of videos streams. In par-

ticular, considerable interest has been focused in ex-

tracting motion related information such as object

and camera motion. Moving objects trajectories have

been used for video retrieval in (Hu et al., 2007) as

well as, camera motion pattern characterization has

been efﬁciently applied for video data indexing and

retrieval in (Tan et al., 2000; Kim et al., 2000). In

(Duan et al., 2006), the motion vectors ﬁeld is used

as a camera motion representation and the detected

motion pattern is classiﬁed using Support Vector Ma-

chines (SVMs) in one of the following classes: zoom,

pan, tilt and rotation. In (Tan et al., 2000) and (Kim

et al., 2000) camera motion estimation within video

shots is performed in the compressed MPEG video

streams, without full frame decompression, using the

motion vector ﬁelds acquired from the P- and B-

video frames. These methods rely on the exploitation

of motion vectors distribution or on a few representa-

tive global motion parameters. However, one of the

main shortcomings of these approaches is that they

are generally not resilient in the presence of mobile

objects of signiﬁcant size and data outliers.

Camera motion can be assumed as a dynamic sys-

Research was supported by the project SHARE: Mo-

bile Number FP6-004218.

tem, whose state θ

is described at time t by the

state vector: θ





where parameters {m

} corre-

spond to the afﬁne transform coefﬁcients, containing

all the relevant information required to describe the

camera motion within frames. Our goal is to recur-

sively estimate the system state θ

from noisy mea-

surements Y

, obtained by an observation model. To

tackle this problem, we propose a novel stochastic

vector ﬁeld model applied in a particle ﬁlters frame-

work.

2 PROBLEM FORMULATION

In order to measure the displacement between two

consecutive frames, we employ the motion vectors

derived by a motion compensation algorithm such as

block matching (Jain and Jain, 1981). A motion vec-

tor v

= [v

]

represents the displacement of the

i-th block in relative coordinates between two consec-

utive video frames f

t−1

and f

as: x

′

= x

+ v

, y

′

+ v

where (x

) and (x

′

) are the coordinates of

i-th block center at frame f

t−1

and f

, respectively.

We can represent the displacement of the i

block

by a 2D afﬁne transform as:

′

0 0 1

⇔

− 1 m

0 0 0

. (1)

670

Nikitidis S., Zafeiriou S. and Pitas I. (2008).

CAMERA MOTION ESTIMATION USING PARTICLE FILTERS.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 670-673

DOI: 10.5220/0001086906700673

 SciTePress

We seek an afﬁne transformation matrix M such

that to approximate BM ≈ B+ V, where B is a n× 3

matrix (n is the number of blocks that each frame

has been divided to) containing the center coordi-

nates of each block. Matrix V = [v

0] contains

the motion vectors, where v

= [v

...v

]

and

= [v

...v

]

are n × 1 vectors containing the

motion vectors residuals along to the x and y axes, re-

spectively. M = [M

e] is the 3×3 afﬁne transfor-

mation matrix, where M

= [m

]

, M

]

and e = [0 0 1]

3 ONLINE VECTOR FIELD

MODEL

The presented Online Vector Field Model (OVFM)

exploits temporal characteristics of camera motion.

OVFM is time-varying and comprises of three dif-

ferent components OVFM

= {S

} which are

combined in a probabilistic mixture model.

3.1 Probabilistic Mixture Model

The stable component S

= {S

t,x

t,y

} learns a

smooth camera motion pattern obtained from a rela-

tively long period of the video sequence. The compo-

nent S

comprises of vectors S

t,x

= [s

t,x

...s

t,x

]

and S

t,y

= [s

t,y

...s

t,y

]

where values s

t,x

and s

t,y

contain the block j displacement momentum along

the x and y axes, respectively. The wander component

= {W

t,x

t,y

}, identiﬁes sudden motion changes,

and adapts with a short time observation sequence, as

a two frame motion change model. Vectors W

t,x

...w

t,x

]

and W

t,y

= [w

t,y

...w

t,y

]

contain the motion vectors residuals, along the x and

y axes, respectively. Finally, the lost component L

t,x

t,y

} is ﬁxed and represents the ideal stationary

video scene.

We model the probability density function for the

, W

and L

components with the bivariate Gaussian

distribution N(v

;µ

c,t

∑

c,t

) c ∈ {S

}, where

∑

c,t

is a 2× 2 covariance matrix referred to c-th com-

ponent j-th motion vector containing the two random

variables v

and v

, µ

c,t

denotes the mean value of the

j-th motion vector. OVFM

combines probabilisti-

cally components S

, W

and L

according to the for-

mula:

P(Y

|θ

) =

∏

j=1



P(v

) + P(v

)



∏

j=1



∑

c=S,W,L

c,t,xy



;µ

c,t

∑

c,t





, (2)

where Y

= [v

...v

]

is the observation data derived

for state θ

. The mixing probabilities m

c,t,xy

regu-

late the contribution that each component j-th mo-

tion vector makes to the complete observation like-

lihood at time t and n is the number of motion vec-

tors. OVFM

is embedded in the particle ﬁlters frame-

work evaluating each potential future state of the sys-

tem. A state estimate

is generated by ﬁrst drawing

a Gaussian noise sample U

t−1

and applying the state

transition function

= E

t−1

(θ

t−1

). Each state

estimate

determined by particle i is being evalu-

ated with respect to the available motion representa-

tion in OVFM

, by computing the observation likeli-

hood according to equation (2). Weights are assigned

to particles by applying the Sequential Importance

Re-sampling ﬁlter (SIR) proposed in (Gordon et al.,

1993), as: w

∝ P(Y

|θ

), w

∑

i=1

3.2 Online Model Update

We assume that OVFM

has limited memory over

the past motion observations and when newer infor-

mation is available, previous knowledge is forgot-

ten and is combined with newer observations using

the exponential envelop E

(k) = αe

(−(t−k)/τ)

where

τ = n

/log2, n

is the envelope’s half life in video

frames and parameter α is deﬁned as α = 1 − e

−1/τ

in order the ownership posterior probabilities and the

mixing probabilities to sum to 1. The posterior own-

ership probabilities O

c,t

denote the contribution that

each component motion vector makes to the complete

observation likelihood. Ownerships are evaluated by

applying the EM algorithm in (Dempster et al., 1977)

as:

c,t,xy

∝ m

c,t,xy

N(v

;µ

c,t

∑

c,t

c,t,x

∝ m

c,t,x



t,x

;µ

c,t,x

,(σ

c,t,x

)



c,t,y

∝ m

c,t,y



t,y

;µ

c,t,y

,(σ

c,t,y

)



(3)

where N



t,x

;µ

c,t,x

,(σ

c,t,x

)



is the normal den-

sity function. The ownerships are subsequently used

for updating the mixing probabilities as:

c,t+1,x

= αO

c,t,x

+ (1− α)m

c,t,x

c,t+1,y

= αO

c,t,y

+ (1− α)m

c,t,y

c,t+1,xy

= αO

c,t,xy

+ (1− α)m

c,t,xy

(4)

We compute the new mean values and the new co-

variance matrices for each motion vector by utilizing

the ﬁrst and second order data moments computed as:

CAMERA MOTION ESTIMATION USING PARTICLE FILTERS

671

1,t+1,x

= αO

S,t,x

t,x

+ (1− α)M

1,t,x

1,t+1,y

= αO

S,t,y

t,y

+ (1− α)M

1,t,y

1,t+1,xy

= αO

S,t,xy

t,x

t,y

+ (1− α)M

1,t,xy

2,t+1,x

= αO

S,t,x

t,x

)

+ (1− α)M

2,t,x

2,t+1,y

= αO

S,t,y

t,y

)

+ (1− α)M

2,t,y

(5)

The stable component is updated using the ﬁrst or-

der data moments as:

t+1,x

= µ

S,t+1,x

1,t+1,x

S,t+1,x

t+1,y

= µ

S,t+1,y

1,t+1,y

S,t+1,y

. (6)

The stable component new covariance matrices

are evaluated as:

(σ

S,t+1,x

)

2,t+1,x

S,t+1,x

− (s

t+1,x

)

(σ

S,t+1,y

)

2,t+1,y

S,t+1,y

− (s

t+1,y

)

(σ

S,t+1,xy

)

1,t+1,xy

S,t+1,xy

− (s

t+1,x

)(s

t+1,y

). (7)

The wander component contains the current mo-

tion vectors, since it adapts as a two frame motion

change model, while covariance matrices for the wan-

der and lost components are updated according to sta-

ble component’s covariance matrices in order to avoid

some prior preference in either component.

4 EXPERIMENTAL RESULTS

We have evaluated the efﬁciency of our algorithm

through experimental testing. Experiments have been

conducted in a dataset comprised of infrared video

streams captured by a hand-held video camera. We

present the results obtained by applying our method in

a video sequence containing 485 frames, where cam-

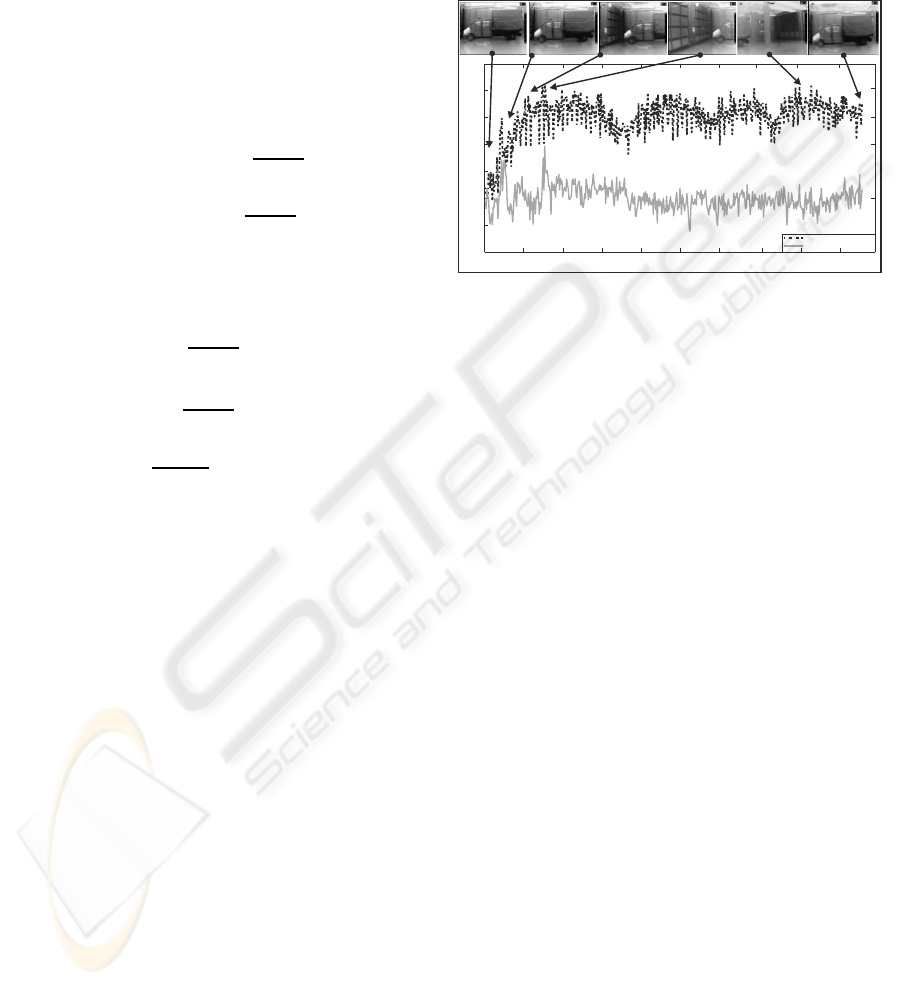
era performs a 360 degrees spin. Figure 1 presents

the variation of the estimated afﬁne coefﬁcients de-

scribing the translation over the x axis (dotted black

line) and y axis (solid gray line) as the video stream

evolves, while at speciﬁc moments the respective

video frames are provided for visual conﬁrmation of

the obtained results. As it is depicted both parameters

balances around zero during the ﬁrst 25 frames since

the camera remains almost still. A radical incense-

ment in the coefﬁcient describing translation over the

x axis occurs from frame 26 and until the end of the

video stream since camera starts to spin. On the other

hand, the coefﬁcient that corresponds to translation

over the y axis continuously balances around zero

since there is minimum movement towards that direc-

tion.

0 50 100 150 200 250 300 350

400 450 500

-1

-0.5

0.5

1.5

2.5

Frame index

Translation factor

Translation in x axis

Translation in y axis

Figure 1: Variation of the translation afﬁne coefﬁcients.

5 CONCLUSIONS

n this paper a novel camera motion estimation method

based in motion vector ﬁelds exploitation is pro-

posed. The features that distinguish our method from

other proposed camera motion estimation techniques

are: 1) the integration of a novel stochastic vector

ﬁeld model, 2) the incorporation of the vector ﬁeld

model inside a particle ﬁlters framework enabling the

method to estimate the future camera movement.

REFERENCES

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).

Maximum likelihood from incomplete data via the em

algorithm. Journal of the Royal Statistical Society. Se-

ries B (Methodological), 39(1):1–38.

Duan, L.-Y., Jin, J. S., Tian, Q., and Xu, C.-S. (2006). Non-

parametric motion characterization for robust classiﬁ-

cation of camera motion patterns. IEEE Transactions

on Multimedia, 8(2):323–340.

Gordon, N., Salmond, D., and Smith, A. (1993). Novel ap-

proach to nonlinear/non-Gaussian bayesian state esti-

mation. In Radar and Signal Processing, IEEE Pro-

ceedings F, volume 140, pages 107–113.

Hu, W., Xie, D., Fu, Z., Zeng, W., and Maybank, S.

(2007). Semantic-based surveillance video retrieval.

IEEE Transactions on Image Processing, 16(4):1168

– 1181.

Jain, J. R. and Jain, A. K. (1981). Displacement mea-

surement and its application in interframe image cod-

ing. IEEE Transactions on Communications, COM-

29(12):1799–1808.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

672

Kim, J.-G., Chang, H.-S., Kim, J., and Kim, H.-M. (30 July-

2 Aug. 2000). Efﬁcient camera motion characteriza-

tion for mpeg video indexing. In ICME 00, volume 2,

pages 1171–1174.

Tan, Y.-P., Saur, D. D., Kulkarni, S. R., and Ramadge, P. J.

(2000). Rapid estimation of camera motion from com-

pressed video with application to video annotation.

IEEE Transactions on Circuits and Systems for Video

Technology, 10(1):133–145.

CAMERA MOTION ESTIMATION USING PARTICLE FILTERS

673