
PROJECTIVE IMAGE ALIGNMENT
BY USING
ECC MAXIMIZATION
Georgios D. Evangelidis and Emmanouil Z. Psarakis
Department of Computer Engineering and Informatics, University of Patras, 26500 Rio, Patras, Greece
Keywords:
Image alignment, image registration, motion estimation, parametric motion, image matching, mosaic con-
struction, gradient methods, correlation coefficient.
Abstract:
Nonlinear projective transformation provides the exact number of desired parameters to account for all possible
camera motions thus making its use in problems where the objective is the alignment of two or more image
profiles to be considered as a natural choice. Moreover, the ability of an alignment algorithm to quickly and
accurately estimate the parameter values of the geometric transformation even in cases of over-modelling of
the warping process constitutes a basic requirement to many computer vision applications. In this paper the
appropriateness of the Enhanced Correlation Coefficient (ECC) function as a performance criterion in the
projective image registration problem is investigated. Since this measure is a highly nonlinear function of the
warp parameters, its maximization is achieved by using an iterative technique. The main theoretical results
concerning the nonlinear optimization problem and an efficient approximation leading to an optimal closed
form solution (per iteration) are presented. The performance of the iterative algorithm is compared against
the well known Lucas-Kanade algorithm with the help of a series of experiments involving strong or weak
geometric deformations, ideal and noisy conditions and even over-modelling of the warping process. In all
cases ECC based algorithm exhibits a better behavior in speed, as well as in the probability of convergence as
compared to the Lucas-Kanade scheme.
1 INTRODUCTION
The image alignment problem can be seen as a map-
ping between the coordinates systems of two or more
images, therefore the first step towards its solution
is the choice of an appropriate geometric transfor-
mation that adequately models this mapping. Eight-
parameters projective transformation provides the e-
xact number of desired parameters to account for all
possible camera motions, therefore its use in the para-
metric image alignment problem is considered as the
most natural choice. This class of transformations and
in particular several of its subclasses as affine, simi-
litude transformations and pure translation have been
in the center of attention in many applications (Fuh
and Maragos, 1991; Gleicher, 1997; Hager and Bel-
humeur, 1998; Baker and Matthews, 2004; Szeliski,
2006).
Once the parametric transformation has been de-
fined the alignment problem reduces into a parame-
ter estimation problem. Therefore, the second critical
step towards its solution is the definition of an appro-
priate objective function. Most existing techniques
adopt measures which are l
p
based norms of the er-
ror between either the whole image profiles (pixel-
based techniques) or specific feature of image pro-
files (feature-based techniques) (Szeliski, 2005), with
the l
2
norm being by far the most widely used (Lucas
and Kanade, 1981; Anandan, 1989; Fuh and Mara-
gos, 1991; Hager and Belhumeur, 1998; Shum and
Szeliski, 2000; Baker and Matthews, 2004; Szeliski,
2006; Evangelidis and Psarakis, 2007).
Independently of the used measure, for the opti-
mum estimation of the parameters most of the exist-
ing pixel-based techniques require the use of gradient
based iterative optimization techniques. However, the
choice of the measure, the form of the alternative ex-
pression that approximates the original nonlinear ob-
jective function in each iteration of the alignment a-
lgorithm and the number of the parameters to be e-
stimated, affect its accuracy, speed and probability of
convergency as well as its robustness against possible
photometric distortions.
413
Evangelidis G. and Psarakis E. (2008).
PROJECTIVE IMAGE ALIGNMENT BY USING ECC MAXIMIZATION.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 413-420
DOI: 10.5220/0001087204130420
Copyright
c
SciTePress

In this paper the appropriatenessof Enhanced Cor-
relation Coefficient (Evangelidis and Psarakis, 2007)
as a performance criterion for the eight-parameters
nonlinear projective registration problem is inve-
stigated. Since the measure is a highly nonlinear
function of the warp parameters, its maximization is
achieved by using an iterative technique. The main
theoretical results concerning the nonlinear optimiza-
tion problem and an efficient approximation that leads
to an optimal closed form solution (per iteration) are
presented. The performance of the algorithm is co-
mpared against the well known Lucas-Kanade algo-
rithm with the help of a series of experiments. In all
experiments the eight-parameters mentioned transfor-
mation is used to model the warping process. Two
sets of experiments are conducted. That differentiates
these sets is the class of the transformations we use
to create the image profiles. Specifically, in the first
set of experiments the reference image profiles are
created by using a nonlinear projective transforma-
tion (minimal case). In the second set of experiments
(over-modelling case), in order to quantify the impact
of mismatches between the actual motion model and
that used by the algorithms, reference image profiles
are created by using affine transformations and the be-
havior of the iterative algorithms under the influence
of over modelling is examined.
The remainder of this paper is organized as fol-
lows. In Section 2, we formulate the parametric ima-
ge alignment problem. In Section 3, the ECC based
nonlinear optimization problem is defined; the itera-
tive alignment algorithm and a closed form optimal
solution of the basic (per iteration) optimization pro-
blem are given. In Section 4, we apply the ECC based
technique in a number of experiments and a detailed
comparison of our algorithm with the Lucas-Kanade
alignment scheme is provided. Finally, Section 5 co-
ntains our conclusions.
2 PROBLEM FORMULATION
In this section we formulate the problem of alignment
of two image profiles. Let us assume that a refer-
ence image I
r
(x) and a warped image I
w
(x
′
) are given,
where x = [x, y] and x
′
= [x
′
, y
′
] denote image coordi-
nates. Suppose also that we are given a set of coordi-
nates S = {x
i
| i = 1, . . . , K} in the reference image,
which is called target area. Then, the alignment prob-
lem consists in finding the corresponding coordinate
set in the warped image.
By considering that a transformation model
T(x;p) where p = (p
1
, p
2
, . . . , p
N
)
t
is a vector of un-
known parameters is given, the alignment problem is
reduced to the problem of estimating the parameter
vector p such that
I
r
(x) = Ψ(I
w
(T(x;p));α), x ∈ S , (1)
where transformation Ψ(I, α) which is parameterized
by a vector α, accounts for possible photometric dis-
tortions that violate the brightness constancy assump-
tion, a case which arises in real applications due to
different viewing directions and/or different illumina-
tion conditions.
The goal of most existing algorithms is the mini-
mization of the dissimilarity of the two image profiles,
providing the optimum parameter values. Dissimi-
larity is usually expressed through an objective func-
tion E(p, α) which involves the l
p
norm of the inten-
sity residual of the image profiles. A typical mini-
mization problem has the following form
min
p,α
E(p, α) = min
p,α
∑
x∈S
|I
r
(x) − Ψ(I
w
(T(x;p)), α) |
p
.
(2)
Solving the above defined problem is not a simple
task because of the nonlinearity involved in the cor-
respondence part. Computational complexity and e-
stimation quality of existing schemes depends on the
specific l
p
norm and the models used for warping and
photometric distortion. As far as the norm power p is
concerned most methods use p = 2 (Euclidean norm).
This will also be the case in the approach we briefly
present in the next section.
3 THE ALIGNMENT
ALGORITHM
It is more convenient at this point to define the refe-
rence vector i
r
and the warped vector i
w
(p) as follows
i
r
=
I
r
(x
1
)
I
r
(x
2
)
.
.
.
I
r
(x
K
)
, i
w
(p) =
I
w
(T(x
1
;p))
I
w
(T(x
2
;p))
.
.
.
I
w
(T(x
K
;p))
(3)
and denote by
¯
i
r
and
¯
i
w
(p) the zero-mean versions of
the reference and warped vector respectively. We then
propose the following l
2
based criterion to quantify
the performance of the warping transformation with
parameters p
E
ECC
(p) =
¯
i
r
||
¯
i
r
||
−
¯
i
w
(p)
||
¯
i
w
(p)||
2
, (4)
where || · || denotes the usual Euclidean norm.
It is clear from (4) that this criterion is invariant to
possibly existing contrast and/or brightness changes
since involved vectors are zero-mean and normalized.
This characteristic clearly support our choice to adopt
this criterion for the image alignment problem.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
414

3.1 A Nonlinear Maximization Problem
Since the residual in (4) is based on zero-mean and
normalized vectors, it is straightforward to prove that
minimizing E
ECC
(p) is equivalent to maximizing the
enhanced correlation coefficient (Psarakis and Evan-
gelidis, 2005)
ρ(p) =
ˆ
i
t
r
¯
i
w
(p)
||
¯
i
w
(p)||
(5)
where
ˆ
i
r
is the normalized reference vector. Notice
that even if
¯
i
w
(p) depends linearly on the parameter
vector p, the resulting objective function is still non-
linear with respect to p due to the normalization of the
warped vector. This of course suggests that its maxi-
mization requires nonlinear optimization techniques.
In order to maximize ρ(p) we are going to use
a gradient-based iterative approach. More specifi-
cally, we are going to replace the original optimiza-
tion problem by a sequence of secondary optimiza-
tions. Each such optimization relies on the outcome
of its predecessor thus generating a sequence of pa-
rameter estimates which hopefully converges to the
desired optimizing vector of the original problem.
Notice that, at each iteration we do not have to op-
timize the objective function, but an approximation
to this function, such that the resulting optimizer are
simple to compute. Let us therefore introduce the ap-
proximation we intend to apply to our objective func-
tion and also derive an analytic expression for the so-
lution that maximizes it.
Suppose that p is “close” to some nominal param-
eter vector
˜
p and write p =
˜
p+ ∆p, where ∆p denotes
a vector of perturbation. Suppose also that the in-
tensity function I
w
and the warping transformation T
are of sufficient smoothness to allow for the existence
of the required partial derivatives. If we denote as
˜x
′
= T(x;
˜
p) the warped coordinates under the nom-
inal parameter vector and x
′
= T(x;p) under the pe-
rturbed, then, applying a first order Taylor expansion
with respect to the parameters, we can write
I
w
(x
′
) ≈ I
w
(
˜
x
′
) +
∇
x
′
I
w
(
˜
x
′
)
t
∂T(x;
˜
p)
∂p
∆p, (6)
where ∇
x
′
I
w
(
˜
x
′
) denotes the gradient vector of length
2 of the intensity function I
w
(x
′
) of the warped image
evaluated at the nominal coordinates
˜
x
′
and
∂T(x;
˜
p)
∂p
the
size 2× N Jacobian matrix of the warp transform with
respect to its parameters, evaluated at the nominal val-
ues
˜
p.
By applying (6) to all points of target area S , fo-
rming the linearized version of the warp vector i
w
(p)
and computing its zero mean counterpart we obtain
the following approximation ρ(∆p|
˜
p) of the objective
function ρ(p) defined in (5):
ρ(p) ≈ ρ(∆p|
˜
p) =
ˆ
i
t
r
¯
i
w
+
ˆ
i
t
r
¯
G∆p
q
k
¯
i
w
k
2
+ 2
¯
i
t
w
¯
G∆p+ ∆p
t
¯
G
t
¯
G∆p
(7)
where
¯
G denotes the column-zero-mean counterpart
of the size K × N Jacobian matrix G(
˜
p) of the warped
intensity vector with respect to the parameters, evalu-
ated at the nominal parameter values
˜
p. Note that for
notational simplicity, the dependence of the warped
vectors on p has been dropped.
Although ρ(∆p|
˜
p) is a non-linear function of ∆p,
its maximization results in a closed-form solution.
This solution is given, without proof, by the next the-
orem (Evangelidis and Psarakis, 2007).
Theorem I: Consider the objective function de-
fined in (7) and the orthogonal projection matrix P
G
=
¯
G(
¯
G
t
¯
G)
−1
¯
G
t
of size K. Then, as far as the maximal
value of ρ(∆p|
˜
p) is concerned, we distinguish the fol-
lowing two cases: Case
ˆ
i
t
r
¯
i
w
>
ˆ
i
t
r
P
G
¯
i
w
: here we have
a maximum, specifically
max
∆p
ρ(∆p|
˜
p) =
s
(
ˆ
i
t
r
¯
i
w
−
ˆ
i
t
r
P
G
¯
i
w
)
2
k
¯
i
w
k
2
−
¯
i
t
w
P
G
¯
i
w
+
ˆ
i
t
r
P
G
ˆ
i
r
, (8)
which is attainable for the following optimal pertur-
bation
∆p
o
= (
¯
G
t
¯
G)
−1
¯
G
t
k
¯
i
w
k
2
−
¯
i
t
w
P
G
¯
i
w
ˆ
i
t
r
¯
i
w
−
ˆ
i
t
r
P
G
¯
i
w
ˆ
i
r
−
¯
i
w
. (9)
Case
ˆ
i
t
r
¯
i
w
≤
ˆ
i
t
r
P
G
¯
i
w
: here we have a supremum,
specifically
sup
∆p
ρ(∆p|
˜
p) =
q
ˆ
i
t
r
P
G
ˆ
i
r
, (10)
which can be approached arbitrarily close by sele-
cting
∆p
o
= (
¯
G
t
¯
G)
−1
¯
G
t
λ
ˆ
i
r
−
¯
i
w
, (11)
with λ a positive scalar, of sufficiently large value.
In order to be able to use the results of Theorem I
the positive quantity λ must be defined. It is clear that
λ must be selected so that the resulting ρ(∆p
o
|
˜
p) sati-
sfies ρ(∆p
o
|
˜
p) > ρ(0|
˜
p) and ρ(∆p
o
|
˜
p) ≥ 0. Possible
values of λ provide the following lemma (Evangelidis
and Psarakis, 2007).
Lemma I: Let
ˆ
i
t
r
¯
i
w
≤
ˆ
i
t
r
P
G
¯
i
w
and define the follo-
wing two values for λ
λ
1
=
s
¯
i
t
w
P
G
¯
i
w
ˆ
i
t
r
P
G
ˆ
i
r
, λ
2
=
ˆ
i
t
r
P
G
¯
i
w
−
ˆ
i
t
r
¯
i
w
ˆ
i
t
r
P
G
ˆ
i
r
. (12)
Then for λ ≥ λ
1
we have that ρ(∆p
o
|
˜
p) > ρ(0|
˜
p); for
λ ≥ λ
2
that ρ(∆p
o
|
˜
p) ≥ 0; finally for λ ≥ max{λ
1
, λ
2
}
we have both inequalities valid.
PROJECTIVE IMAGE ALIGNMENT BY USING PROJECTIVE IMAGE ALIGNMENT
415

Let us now translate the above results into an i-
terative scheme in order to obtain the solution to the
original nonlinear optimization problem. To this end,
let us assume that from iteration j − 1 we have avai-
lable the parameter estimate p
j− 1
and we adopt the
following additive rule
p
j
= p
j− 1
+ ∆p
j
. (13)
Then, using p
j− 1
we can compute
¯
i
w
(p
j− 1
)
and
¯
G(p
j− 1
) and optimize the approximation
ρ(∆p
j
|p
j− 1
) with respect to ∆p
j
. The iterative
algorithm is summarized below.
Initialization
· Use I
r
to compute
ˆ
i
r
defined in (3).
· Initialize p
0
and set j = 1.
Iteration Steps
· Using T(x;p
j− 1
) warp I
w
and compute
¯
i
w
(p
j− 1
)
· Using T(x;p
j− 1
) warp the gradient ∇I
w
of I
w
and
compute the Jacobian matrix
¯
G(p
j− 1
)
· Compare
ˆ
i
t
r
¯
i
w
with
ˆ
i
t
r
P
G
¯
i
w
and compute perturba-
tions ∆p
o
j
either from (9) or using (11) and (12)
· Update parameter vector p
j
= p
j− 1
+ ∆p
o
j
.
If k∆p
o
j
k ≥ ε
p
then, j+ + and repeat; else stop.
As it is indicated above, the algorithm is executed
until the norm of the perturbation vector k∆p
o
j
k be-
comes smaller than a predefined threshold ε
p
.
We must stress at this point that the convergence
of the proposed algorithm can critically be affected by
the values of vector p
0
when the images overlap by a
small amount or one image is only a small deformed
subset of the other. In such cases appropriate values of
vector p
0
should prevent the algorithm to be trapped
into local maxima. Such a reliable estimation for
the initialization of the algorithm can be obtained by
using a correlation based search method (Shum and
Szeliski, 2000) or a landmark-based method (John-
son and Christensen, 2002). However, in this paper
we consider that the images overlap by a large amount
thus excluding such cases.
Concluding, the structure of the iterative algo-
rithm is very similar to the forward additive scheme
of the Lucas-Kanade (LK) algorithm (Lucas and
Kanade, 1981), one of the most frequently used algo-
rithm for the image alignment problem, but as we are
going to see in the next section, the proposed updating
scheme improves the performance significantly.
3.2 Parametric Models
In this work, to model the warping process we are
going to use the following eight-parameters projective
transformation (homography)
x
′
= T(x;p) =
1
P
p
1
p
2
p
3
p
4
p
5
p
6
x
1
(14)
where P = p
7
x + p
8
y + 1. This class of transforma-
tions is the most general class of the well known 2-
D planar motion models that gives the exact number
of desired parameters to account for all the possible
camera motions.
For the Jacobian of the projective model we have
∂T(x;p)
∂p
=
1
P
x y 1 0 0 0 −x
′
x −x
′
y
0 0 0 x y 1 −y
′
x −y
′
y
,
(15)
where x
′
, y
′
are the elements of vector x
′
.
As it is clear from (14), eight-parameters proje-
ctive transformation is a nonlinear function of its pa-
rameters and its stability as well as the continuity of
its Jacobian are depended on the values of the deno-
minator P. To ensure its stability and the existence
of its Jacobian, we restrict ourselves on admissible
(Radke et al., 2000) estimations of the transform.
Note also that in spite of the affine model which has a
Jacobian that does not depend on the warping parame-
ters, projective model, as it is obvious from (15), has a
Jacobian that depends on the parameters p and thus it
must be updated on each iteration of the iterative algo-
rithms. Several approximations of projective transfor-
mation such as bilinear and polynomial can be used
in order to partially overcome these problems. Note
though that by following such an approach, the strong
deformations introduced by the projective transfor-
mation cannot be exactly adjusted and this may lead
to meaningless alignment results.
4 SIMULATION RESULTS
In this section we are going to evaluate our algorithm
and compared it against the forward additive version
of the Lucas-Kanade algorithm (Lucas and Kanade,
1981), as it is implemented in (Baker and Matthews,
2004). As we have already mentioned, we perform
two sets of experiments. In both sets, for the mod-
elling of the warping process the nonlinear projec-
tive transformation defined in (14)is used, but in the
first set of experiments the reference image profiles
are created using a nonlinear projective transforma-
tion, while in the second set by using an affine one.
We must stress at this point that for all aspects affe-
cting the simulation experiments, we made an effort
to stay exactly within the frame specified in (Baker
and Matthews, 2004). Before we present our results
we give some details for the experimental setup as
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
416

well as the figures of merit we are going to use in
order to fairly compare the competing algorithms.
4.1 Experimental Setup
The experimental setup is described analytically in
(Baker and Matthews, 2004). In brief, we have an
input image I
0
and we crop a rectangular area of the
image. By adding an appropriate translation in the
coordinates of the points corresponding to the corners
of the cropped image and adding Gaussian noise with
standard deviation σ
p
we perturb them. The four ini-
tial points, and their warped versions defines the pa-
rameter vector of the projective transformation. U-
sing these values, we map all target points and warp
I
0
to create a reference image I
r
. The competing algo-
rithms then are applied for the alignment of I
r
with I
0
.
In order to create a reference image I
r
in the second
set of our experiments, we follow a similar procedure.
Note though that in this case we select three points in-
stead of four, from the rectangular cropped area (i.e.
top left and right corner and bottom middle point) and
use them in order to define the six parameters of the
affine transform.
In order to measure the quality of the estimated
parameters we use the Mean Square Distance (MSD)
between the exact warped version of the four (three)
points and their estimated counterparts. More for-
mally, if we denote as p
r
the parameter vector which
we use in defining the reference profile I
r
, p
j
the cur-
rent estimation of the corresponding algorithm at j-th
iteration and C the set of the four(three) above me-
ntioned points, we use the mean of the following se-
quence
e( j) =
1
8(6)
∑
x∈C
||T(x;p
r
) − T(x;p
j
)||
2
. (16)
Each element of the mean sequence (i.e. for a spe-
cific value of iteration index j) is obtained by aver-
aging over a large number of image pairs that dif-
fer in the noise realization, and captures the learn-
ing ability of the algorithms (average rate of con-
vergence (Baker and Matthews, 2004)). However,
in order to not present biased results, we compute
the above mentioned mean sequence for those rea-
lizations where both algorithms have converged. The
convergence criterion is that the square distance e( j)
at a prescribed maximal iteration j
max
is below a ce-
rtain threshold T
MSD
, that is e( j
max
) ≤ T
MSD
.
As a second figure of merit we use the percentage
of converging (PoC) runs (frequency of convergence
(Baker and Matthews, 2004)). This quantity is the
percentage of runs that converge up to maximal iter-
ation j
max
, based again on the above mentioned con-
vergence criterion. PoC is depicted as a function of
the point deviation σ
p
, the most important factor that
affects the performance of both algorithms.
Since it is natural to prefer an algorithm that con-
verges quickly with high probability, we propose a
third figure of merit that captures exactly this point
(Evangelidis and Psarakis, 2007). In other words we
propose the generation of a histogram depicting the
probability of successful convergence at each itera-
tion. Specifically a run of an algorithm on an im-
age pair realization will be considered as having con-
verged at iteration n when the squared error e( j) goes
below the threshold T
MSD
for the first time at iteration
j = n. It is clear that we prefer a histogram to be con-
centrated over mostly small iteration-numbers.
In all experiments that follow we use T
MSD
=
1 pixel
2
.
4.2 Minimal Case
In this subsection we present the results we obtained
from the first set of experiments we have conducted.
As it is above described, in this case we create the
reference profile by using a projective transform and
we model the warping process by using a transforma-
tion of the same class.
4.2.1 Experiment I
In the first experiment, the alignment algorithms try
to compensate only the geometric distortions since
this is the only that has been applied to images.
Specifically, we use the “Takeo” image (Baker and
Matthews, 2004) as input image and we create 500
different reference profiles for each integer values of
σ
p
in the range [1, 10]. For each one of the 500 rea-
lizations, we permit the algorithms to make 15 itera-
tions (j
max
= 15). Since no intensity noise or photo-
metric distortion is applied to image, we expect MSD
to reach very low levels which cannot be zero due to
finite precision arithmetic.
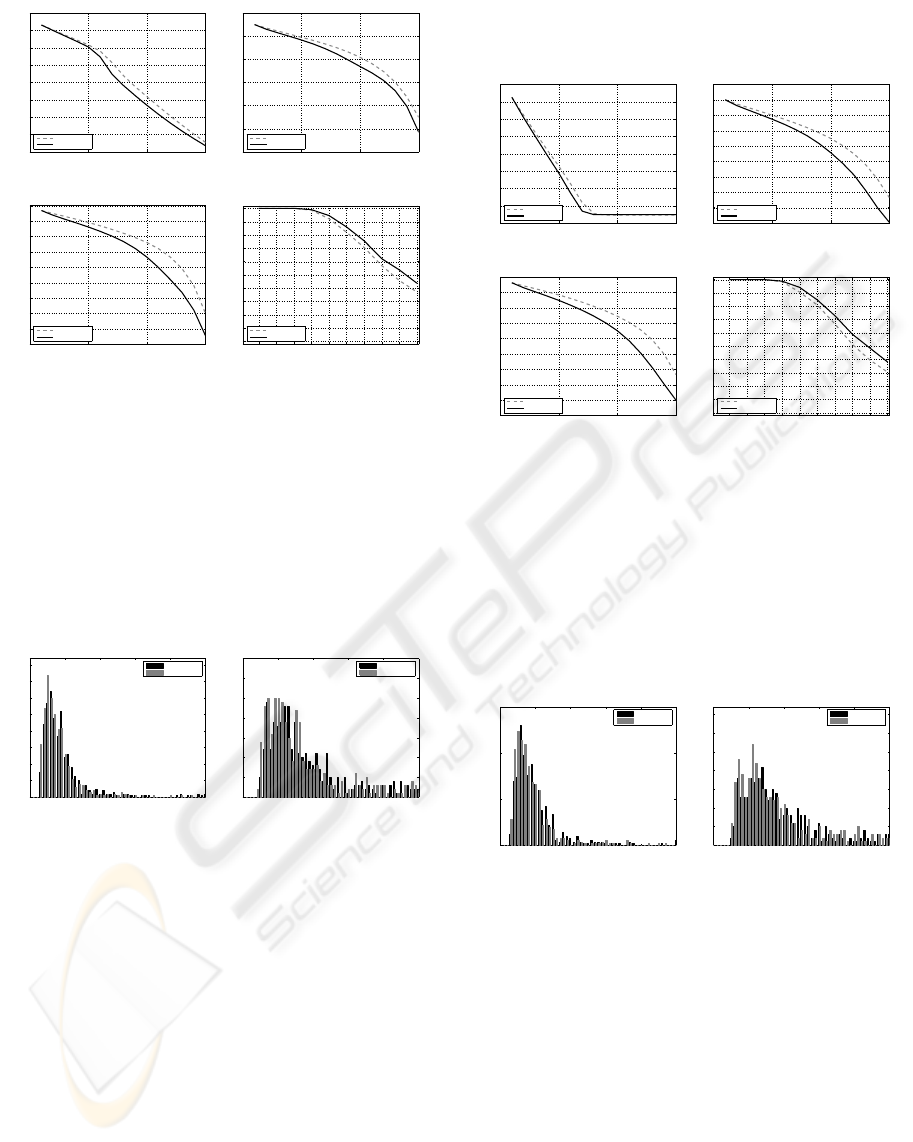
Figure 1 depicts the relative performance of the
two algorithms. As we mentioned above, we present
the arithmetic mean of the sequence e( j) for those
realizations where both algorithms have converged.
Three cases are investigated; (a) σ
p
= 2, (b) σ
p
= 6
and (c) σ
p
= 10. In all these cases our algorithm ex-
hibits a significantly smaller MSD which is order(s)
of magnitude better than the one obtained by the LK
scheme. Furthermore concerning the PoC, as we can
see from Figure 1.(d), our algorithm exhibits better
performance for all values of σ
p
. Specifically for
strong deformations (σ
p
= 10) the improvement can
become quite significant (18%). As far as the proba-
bility of successful convergence is concerned, we ap-
plied the algorithms for a maximal number of 100 it-
erations (j
max
= 100). In Figure 2 the resulting graphs
PROJECTIVE IMAGE ALIGNMENT BY USING PROJECTIVE IMAGE ALIGNMENT
417
0 5 10 15
−140
−120
−100
−80
−60
−40
−20
0
20
Iteration
MSD (in db)
Lucas−Kanade
ECC
(a)
0 5 10 15
−40
−30
−20
−10
0
10
20
Iteration
MSD (in db)
Lucas−Kanade
ECC
(b)
0 5 10 15
−25
−20
−15
−10
−5
0
5
10
15
20
Iteration
MSD (in db)
Lucas−Kanade
ECC
(c)
1 2 3 4 5 6 7 8 9 10
0
10
20
30
40
50
60
70
80
90
100
Point Standard Deviation
PoC
Lucas−Kanade
ECC
(d)
Figure 1: MSD in dB as a function of number of iterations;
(a) σ
p
= 2, (b) σ
p
= 6, (c) σ
p
= 10. In (d), PoC as a function
of σ
p
for j
max
= 15.
for the cases of σ
p
= 6 and σ
p
= 10 are shown. In or-
der however, for the differences to become visible, we
present only the first 50 bins of the histogram. As we
can clearly see the proposed algorithm has larger per-
centage of converged realizations in smaller iteration
numbers than the LK scheme.
0 10 20 30 40 50
0
2
4
6
8
10
12
14
16
Iteration
Successful Convergence (%)
Lucas−Kanade
ECC
(a)
0 10 20 30 40 50
0
1
2
3
4
5
6
7
Iteration
Successful Convergence (%)
Lucas−Kanade
ECC
(b)
Figure 2: Histograms of successful convergence as a func-
tion of number of iterations; (a) σ
p
= 6, (b) σ
p
= 10.
4.2.2 Experiment II
In this experiment we repeat the previous procedure,
but we add now intensity noise to both images before
their alignment. Specifically, the standard deviation
of the noise we add into the images is equal to 8 gray
levels. Due to this noise, even theoretically the MSD
can no longer be equal to 0.
In Figure 3 the results we obtained are shown. For the
case of σ
p
= 2 we observe that both algorithms reach
an MSD floor value, while in the other two cases this
is not visible. Note though that the proposed algo-
rithm outperforms the LK scheme by a half or a full
order of magnitude. Furthermore, the proposed algo-
rithm exhibits a larger PoC score confirming thus its
superiority. Regarding the histograms, as we can see
0 5 10 15
−30
−25
−20
−15
−10
−5
0
5
10
Iteration
MSD (in db)
Lucas−Kanade
ECC
(a)
0 5 10 15
−25
−20
−15
−10
−5
0
5
10
15
20
Iteration
MSD (in db)
Lucas−Kanade
ECC
(b)
0 5 10 15
−25
−20
−15
−10
−5
0
5
10
15
20
Iteration
MSD (in db)
Lucas−Kanade
ECC
(c)
1 2 3 4 5 6 7 8 9 10
0
10
20
30
40
50
60
70
80
90
100
Point Standard Deviation
PoC
Lucas−Kanade
ECC
(d)
Figure 3: MSD in dB as a function of number of iterations
for the noisy (8 gray levels) “Takeo” image; (a) σ
p
= 2,
(b) σ
p
= 6, (c) σ
p
= 10. In (d), PoC as a function of σ
p
for
j
max
= 15.
from Figure 4, the resulting histograms are very simi-
lar to the previous noise-free case with the histograms
of the proposed algorithm having a larger percentage
of convergedrealizations in smaller iteration numbers
than the LK scheme.
0 10 20 30 40 50
0
5
10
15
Iteration
Successful Convergence (%)
Lucas−Kanade
ECC
(a)
0 10 20 30 40 50
0
1
2
3
4
5
6
7
Iteration
Successful Convergence (%)
Lucas−Kanade
ECC
(b)
Figure 4: Histograms of successful convergence as a func-
tion of number of iterations for the noisy (8 gray levels)
“Takeo” image; (a) σ
p
= 6, (b) σ
p
= 10.
4.3 Over-Modelling Case
In this subsection we examine the behavior of the
algorithms under the influence of over-modelling.
Specifically, we create the reference profiles by using
an affine transform, but we still model the warping
process by using a nonlinear projective transforma-
tion. Since six parameters are required for the affine
transform, the values of two more parameters (p
7
, p
8
)
must be estimated by the alignment algorithms. Ide-
ally these values must be equals to zero. Since we like
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
418

to evaluate the performance of the algorithms under
the influence of the over-modelling, we concentrate
ourselves on the realizations where both algorithms
are converged when the warping process is modelled
by an affine transformation. Then, we run the com-
peting algorithms on these common converged rea-
lizations, the converged realizations for each one in
the over-modelling case are counted, and the resu-
lting learning curves and PoC scores are presented.
As far as the probability of convergence is concerned,
as in the minimal case we applied the algorithms for
a maximum of 100 iterations and the resulting his-
tograms are also presented. For comparison purposes,
the learning curves as well as PoC scores obtained
from the affine modelling are superimposed on the
corresponding plots. As in the previous subsection
two experiments are conducted.
4.3.1 Experiment III
This experiment is very similar to Experiment I. As
we already mentioned, the basic difference is that the
reference profiles have been created by using affine
transformations instead of projective ones. As it was
0 5 10 15
−160
−140
−120
−100
−80
−60
−40
−20
0
20
Iteration
MSD (in db)
LK over−modelling
ECC over−modelling
LK affine modelling
ECC affine modelling
500
500
500
(a)
0 5 10 15
−60
−50
−40
−30
−20
−10
0
10
20
Iteration
MSD (in db)
LK over−modelling
ECC over−modelling
LK affine modelling
ECC affine modelling
413
377
321
(b)
0 5 10 15
−30
−25
−20
−15
−10
−5
0
5
10
15
20
Iteration
MSD (in db)
LK over−modelling
ECC over−modelling
LK affine modelling
ECC affine modelling
182
95
156
(c)
1 2 3 4 5 6 7 8 9 10
0
10
20
30
40
50
60
70
80
90
100
Point Standard Deviation
PoC
LK over−modelling
ECC over−modelling
LK affine modelling
ECC affine modelling
(d)
Figure 5: Over-modelling case. MSD in dB as a function of
number of iterations; (a) σ
p
= 2, (b) σ
p
= 6, (c) σ
p
= 10.
In (d), PoC as a function of σ
p
for j
max
= 15.
expected (Figure 5), over-modelling degrades the per-
formance of the estimation, affects PoC score as well
as the learning ability of the algorithms. However,
we observe that ECC algorithm seems to be more
robust in the over-modelling case than the LK algo-
rithm. Indeed, this is exactly the case if we take into
account the number of realizations in which each al-
gorithm has converged (the values appeared next to
each curve). For example, for the case of σ
p
= 10
(Figure 5.(c)), in a total of 182 common “success-
fully” converged realizations under affine modelling
(Evangelidis and Psarakis, 2007), LK algorithm suc-
ceeded in aligning 95 profiles (52%), while ECC algo-
rithm 156 (86%). Figure 5.(d) depicts the algorithms
PoC as a function of σ
p
for both cases. We observe
that the behavior of ECC algorithm is better as co-
mpared to the LK scheme which exhibits a significant
degradation in its performance due to over-modelling.
In Figure 6 the obtained histograms are shown. As
we can see from Figure 6 the histograms resulting
from the proposed algorithm are more concentrated
over smaller iteration numbers than the histograms re-
sulting from the LK scheme. This is more evident in
Figure 6.(b) where the resulting histogram from the
LK scheme is almost uniformly spread over the range
5 to 30.
0 10 20 30 40 50
0
5
10
15
Iteration
Successful Convergence (%)
Lucas−Kanade
ECC
(a)
0 10 20 30 40 50
0
1
2
3
4
5
6
7
Iteration
Successful Convergence (%)
Lucas−Kanade
ECC
(b)
Figure 6: Over-modelling case. Histograms of successful
convergence as a function of number of iterations; (a) σ
p
=
6, (b) σ
p
= 10.
4.3.2 Experiment IV
The conditions of this experiment are similar to the
conditions of Experiments III, except the fact that we
try to align noisy images, where the standard devia-
tion of the additive noise is 8 gray levels. The ob-
tained simulation results are shown in Figure 7. As
in the previous experiments, ECC algorithm seems to
outperforms the LK scheme. As we can see from the
corresponding figures, ECC based algorithm has con-
verged in more realizations than LK algorithm has.
It is also worth noting from Figure 7.(d) where the
PoC score is depicted, that the performance of ECC
algorithm in the over-modellingcase almost coincides
with the performance of LK algorithm in the case of
affine modelling. Finally, similar conclusion with that
of the previous experiment can be drawn from Fig-
ure 8 where the obtained histograms with the percent-
ages of successful convergence are depicted.
5 CONCLUSIONS
In this paper a recently proposed parametric align-
ment algorithm was used in the projective image re-
PROJECTIVE IMAGE ALIGNMENT BY USING PROJECTIVE IMAGE ALIGNMENT
419

0 5 10 15
−35
−30
−25
−20
−15
−10
−5
0
5
10
Iteration
MSD (in db)
LK over−modelling
ECC over−modelling
LK affine modelling
ECC affine modelling
500
500
500
(a)
0 5 10 15
−35
−30
−25
−20
−15
−10
−5
0
5
10
15
Iteration
MSD (in db)
LK over−modelling
ECC over−modelling
LK affine modelling
ECC affine modelling
393
289
362
(b)
0 5 10 15
−30
−25
−20
−15
−10
−5
0
5
10
15
20
Iteration
MSD (in db)
LK over−modelling
ECC over−modelling
LK affine modelling
ECC affine modelling
152
136
73
(c)
1 2 3 4 5 6 7 8 9 10
0
10
20
30
40
50
60
70
80
90
100
Point Standard Deviation
PoC
LK over−modelling
ECC over−modelling
LK affine modelling
ECC affine modelling
(d)
Figure 7: Over-Modelling case. MSD in dB as a function
of number of iterations for the noisy (8 gray levels) “Takeo”
image; (a) σ
p
= 2, (b) σ
p
= 6, (c) σ
p
= 10. In (d), PoC as a
function of σ
p
for j
max
= 15.
.
0 10 20 30 40 50
0
2
4
6
8
10
12
Iteration
Successful Convergence (%)
Lucas−Kanade
ECC
(a)
0 10 20 30 40 50
0
1
2
3
4
5
6
Iteration
Successful Convergence (%)
Lucas−Kanade
ECC
(b)
Figure 8: Over-Modelling case. Histograms of successful
convergence as a function of number of iterations for the
noisy (8 gray levels) “Takeo” image; (a) σ
p
= 6, (b) σ
p
=
10.
gistration problem. This algorithm aims at maxi-
mizing the Enhanced Correlation Coefficient func-
tion which is a robust similarity measure against both
geometric and photometric distortions. The opti-
mal parameters are obtained by iteratively solving,
a sequence of approximate nonlinear optimization
problems, which enjoy a simple closed-form solu-
tion with low computational cost. The algorithm was
compared against the well known Lucas-Kanade al-
gorithm, through numerous simulation examples in-
volving ideal and noisy conditions, strong and weak
geometric deformations and even over-modelling of
the warping transformation. In all cases the pro-
posed algorithm exhibited a better behavior with an
improvement in speed, as well as in probability of
convergence as compared to the Lucas-Kanade algo-
rithm.
ACKNOWLEDGEMENTS
This work was supported by the General Secretariat
for Research and Technology of Greek Government
as part of the project “XROMA”, PENED 01.
REFERENCES
Anandan, P. (1989). A computational framework and an al-
gorithm for the measurement of visual motion. Inter-
national Journal of Computer Vision, 2(3):283–310.
Baker, S. and Matthews, I. (2004). Lucas-kanade 20 years
on: A unifying framework: Part 1: The quantity ap-
proximated, the warp update rule, and the gradient de-
scent approximation. volume 56, pages 221–255.
Evangelidis, G. D. and Psarakis, E. Z. (2007). Parame-
tric image alignment using enhanced correlation co-
efficient maximization. Submitted to IEEE Trans. on
PAMI, submission TPAMI-0026-0107.
Fuh, C. and Maragos, P. (1991). Motion dislpacement es-
timation using an affine model for image matching.
Optical Engineering, 30(7):881–887.
Gleicher, M. (1997). Projective registration with difference
decomposition. In Proc. of IEEE International Con-
ference on Computer Vision and Pattern Recognition
(CVPR’97). San Juan, Puerto Rico.
Hager, G. D. and Belhumeur, P. N. (1998). Efficient region
tracking with parametric models of geometry and illu-
mination. IEEE Trans. on PAMI, 20(10):1025–1039.
Johnson, H. and Christensen, G. (2002). Consistent land-
mark and intensity-based image registration. IEEE
Transactions on Medical Imaging, 21(5):450–461.
Lucas, B. D. and Kanade, T. (1981). An iterative image
registration technique with an application to stereo
vision. In Proc. of 7th International Joint Conf on
Artificial Intelligence (IJCAI). Vancouver, British
Columbia.
Psarakis, E. Z. and Evangelidis, G. D. (2005). An enhanced
correlation-based method for stereo correspondence
with sub-pixel accuracy. In Proc. of 10th IEEE In-
ternational Conference on Computer Vision (ICCV
2005). Beijing, China.
Radke, R., Ramadge, P., Echigo, T., and Iisaku, S.
(2000). Efficiently estimating projective transfor-
mations. In Proc. of IEEE International Confer-
ence on Image Processing (ICIP’00), pages 232–235.
Vancouver,Canada.
Shum, H. and Szeliski, R. (2000). Construction of
panoramic image mosaics with global and local align-
ment. International Journal on Computer Vision,
36(2):101–130.
Szeliski, R. (2005). Handbook of Mathematical Models of
Computer Vision. Springer. ch. 17.
Szeliski, R. (2006). Image alignment and stitching: A tu-
torial. Foundations and Trends in Computer Graphics
and Computer Vision, 2(1):1–104.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
420
