HIERARCHICAL EVALUATION MODEL FOR 3D FACE

RECOGNITION

S´ıdnei A. Drovetto Jr., Luciano Silva and Olga R. P. Bellon

IMAGO Research Group, Universidade Federal do Paran´a, Curitiba - PR, Brazil

Keywords:

Face recognition, Simulated Annealing, 3D image registration, Surface Interpenetration Measure.

Abstract:

In this paper we propose to perform 3D face matching based on alignments obtained using Simulated

Annealing (SA) algorithm guided by the Mean Squared Error (MSE) with M-estimator Sample Consensus

(MSAC) and the Surface Interpenetration Measure (SIM). The matching score is obtained by calculation of

the SIM after the registration process. Since the SIM is a sensitive measure, it needs a good alignment to give

relevance to its value. Our registration approach tends to reach a near global solution and, therefore, produces

the necessary precise alignments. By analyzing the matching score, the system can identify if the input images

come from the same subject or not. In a veriﬁcation scenario, we use a hierarchical evaluation model which

maximizes the results and reduces the computing time. Extensive experiments were performed on the well-

known Face Recognition Grand Challenge (FRGC) v2.0 3D face database using ﬁve different facial regions:

three regions of the nose; the region of the eyes; and the face itself. Compared to state-of-the-art works, our

approach has achieved a high rank-one recognition rate and a high veriﬁcation rate.

1 INTRODUCTION

Recently, some approaches for 3D face recognition

have used image registration to measure the similar-

ity between faces, often based on MSE or Root Mean

Squared Error (RMSE) (Chang et al., 2006; Chang

et al., 2005; Lu and Jain, 2005; Lu et al., 2006). In

all these approaches, Iterative Closest Point (ICP) is

traditionally applied as the registration method. How-

ever, ICP demands good initial pre-alignment to be

successfully applied, which is not adequate for an

automatic approach. Also, ICP is guided by the

MSE but it was proved (Silva et al., 2005a) that this

measure could allow imprecise local convergence for

range image registration, even when improved ICP-

based approaches are used (Rusinkiewicz and Levoy,

2001; Gelfand et al., 2003). In addition, in (Silva

et al., 2005a) the authors suggest that MSE is a good

measure for starting the image registration process,

but SIM could be more suitable to be used at “the end

of the game” to assess the quality of the registration.

To surpass these limitations, we developed an

approach for 3D face registration that uses the

SIM (Silva et al., 2005a) to measure the similarity

between facial regions. Also, since SIM is a sensi-

tive measure, a good ﬁnal alignment is required for it

to produce a reliable value. Then, this precise align-

ment is achieved using a SA based approachfor image

registration. In the last stage of the registration pro-

cess, the goal of SA is to maximize SIM and, there-

fore, the similarity between the faces can be reliably

calculated. Very extensive results and comparisons

between ICP and SIM-based registration approaches

can be found in (Silva et al., 2005b).

The two main functionalities of biometric systems

are handled in different ways in our approach. First,

for the veriﬁcation scenario, we employ a hierarchi-

cal evaluation model that analyzes, separately, only

the segmentation results that are relevant to make the

correct decision. Then, for the recognition scenario,

the matching score is calculated for each segmenta-

tion result and after that, all of them are combined

into one score that is used for identiﬁcation.

Extensive experiments were performed on the

well-known FRGC v2.0 3D face database. The ex-

perimental results showed that our approach pro-

duces good results for both recognition and veriﬁ-

cation scenarios when compared to state-of-the-art

works (Chang et al., 2006; Chang et al., 2005; Lu and

Jain, 2005; Lu et al., 2006).

This paper is organized as follows. First, in sec-

tion 2, we review some related works. Next, we in-

troduce our 3D face matching approach in section 3.

For a veriﬁcation scenario, we have adopted a hi-

A. Drovetto Jr. S., Silva L. and R. P. Bellon O. (2008).

HIERARCHICAL EVALUATION MODEL FOR 3D FACE RECOGNITION.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 67-74

DOI: 10.5220/0001087900670074

 SciTePress

erarchical evaluation model that is described in sec-

tion 4. The experimental results summarizing the ob-

tained rates for recognition and veriﬁcation problems

are presented in section 5, followed by the ﬁnal re-

marks in section 6.

2 RELATED WORKS

In (Chang et al., 2006; Chang et al., 2005) the authors

propose the use of three overlapping regions around

the nose — circular nose region, elliptical nose region

and nose region — to overcome the facial expression

problem, since these regions are approximately rigid

across expression variation. The matching score for

each region are combined to improve the accuracy.

The steps involved in this approach are: (1) face ex-

traction: using skin detection applied to the 2D image;

(2) curvature based segmentation and landmark detec-

tion; (3) pose correction: the extracted face is aligned,

using ICP, to a generic 3D face model; (4) extraction

of nose regions based on the landmarks; (5) registra-

tion of surfaces: the registration is accomplished by

ICP and the matching score is the resulting RMSE.

Combining the three nose regions, this approach

achieved a rank-one recognition rate of 97.1% and

a Equal Error Rate (EER) of approximately 0.12%

using only neutral expression images (Chang et al.,

2006). The neutral expression database used in the

experiments consists of 2,798 images of 546 subjects.

The images were divided into one gallery, with 449

images, and nine probe sets totalizing 2,349 images.

In (Lu and Jain, 2005; Lu et al., 2006) the 2D

and 3D images are used to perform face recogni-

tion. ICP is used to match the 3D data and Linear

Discriminant Analysis (LDA) employed to match the

2D images. The combination of the values is done

using the weighted sum rule (Kittler et al., 1998).

This approach is composed by three steps: (1) coarse

alignment based on feature points (obtained manu-

ally); (2) ﬁne alignment: using a modiﬁed version

of ICP which alternates point-to-point distance (Besl

and McKay, 1992) and point-to-plane distance (Chen

and Medioni, 1992); (3) LDA match on a dynamically

generated gallery; (4) integration. The matching score

for the 3D data is the RMSE of the point-to-plane dis-

tance provided by ICP.

By integrating ICP and LDA matching scores, this

approach obtained a rank-one recognition rate of 99%

using only neutral expression frontal face views. The

gallery is composed by 200 3D face models and the

probe has 99 neutral expression frontal images.

As we can see, both approaches are based on

RMSE values provided by ICP and achieve a high

rank-one recognition rate. Also, both approaches

have performed experiments using images contain-

ing facial expressions, but their best results, presented

above, were obtained using only neutral expression

images.

3 3D FACE MATCHING

We propose to perform 3D face matching by combin-

ing a precise registration technique and the SIM (Bel-

lon et al., 2006) to evaluate different facial regions.

The registration is obtained by a SA based approach,

which have two important advantages: (1) it tends to

ﬁnd a near global solution; (2) it can be easily inte-

grated with different kinds of estimators. We use two

robust measures in our SA approach. First the MSAC

is combined with the MSE for a coarse alignment and

latter SIM is applied to achieve a ﬁne registration. The

matching score is given by the SIM value of the ﬁ-

nal alignment for the two images. The SIM is used

as matching score because it produces a better range

for discrimination between faces, when compared to

other metrics.

3.1 The Surface Interpenetration

Measure

The SIM was developed by analyzing visual results

of two aligned surfaces, each rendered in a different

color, crossing over each other repeatedly in the over-

lapping area (Silva et al., 2005b). The interpenetra-

tion effect results from the nature of real range data,

which presents slightly rough surfaces with small lo-

cal distortions caused by limitations of the acquiring

system. Because of this, even ﬂat surfaces present a

“roughness” in range images. With this, we can as-

sume that independently of the shape of the surfaces

the interpenetration will always occur. It was also ob-

served that two images acquired from the same object

surface using the same scanner position and parame-

ters provide two different range images.

By quantifying interpenetration, one can evaluate

more precisely the registration results and provide a

highly robust control (Silva et al., 2005a). To do

this it was developed the following measure based on

the surface normal vector, computed by a local least

squares planar ﬁt, at each point. After the alignment

of two images, A and B, it is identiﬁed the set of in-

terpenetrating points in A with respect to B. For each

point p ∈ A it is deﬁned a neighborhoodN

as a small

n× n window centered on p. With q denoting a point

in the neighborhood N

, c the corresponding point of

p in image B and~n

the local surface normal at c, the

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

set of interpenetrating points is deﬁned as:

(A,B)

= {p ∈ A | [(

−−−→

− c)·~n

][(

−−−→

− c)·~n

] < 0} (1)

where q

∈ N

and i 6= j. This set comprises those

points in A whose neighborhoods include at least one

pair of points separated by the local tangent plane,

computed at their correspondents in B, as can be seen

in the diagram of Figure 1.

Figure 1: Interpenetrating point p in A with respect to B.

With this, the SIM is deﬁned as the fraction of in-

terpenetrating points in A:

SIM

(A,B)

|A|

(2)

In this paper some constraints were applied to the

SIM as suggested in (Silva et al., 2005b) to avoid in-

correct corresponding points, and to obtain more pre-

cise alignments. It was included the constraint m = 5

as the maximum angle allowed between the normal

vectors at c and p, ~n

and ~n

, respectively. Then,

we have p ∈ C only if cos

−1

(~n

·~n

) ≤ m. Also, it

was used a constraint to eliminate the corresponding

points on the surfaces boundaries. In this case, p ∈ C

if c /∈ D, where D is the set of boundary points in B,

and the thickness of the boundary deﬁned as s = 1;

Registrations of two range images presenting

good interpenetration have high SIM values. The

experimental results show that erroneous alignments

produce low SIM values and that small differences in

MSE can yield signiﬁcant differences in SIM. Fur-

thermore, alignments with high SIM present a very

low interpoint distance between the two surfaces.

That is, SIM is a far more sensitive indicator of align-

ment quality when comparing “reasonable” align-

ments (Silva et al., 2005a; Bellon et al., 2005).

3.2 SA-Based Registration

SA (Kirkpatrick et al., 1983) is a stochastic algorithm

for local search in which, from an initial candidate so-

lution, it generates iterative movements to a neighbor

solution that represents a better solution to the prob-

lem as compared to the current one. The main dif-

ference between SA and other local search algorithm,

e.g. Hill Climbing, is that SA can accept a worse solu-

tion than the current candidate in the iterative process.

Then, SA does not remain “tied” to local minima and

because of this it has better chances to reach its goal,

which is a solution close enough to the global one.

In order to apply SA on registration of two range

images, six parameters (three parameters each for ro-

tation and translation relative to a 3D coordinate sys-

tem) are needed to deﬁne the candidate solutions as

a “transformation vector” that, when applied to one

image, can align it with the other.

Our SA-based approach was developed using the

GSL Library

adopting a coarse-to-ﬁne strategy and

has three main stages: (1) pre-alignment; (2) coarse

alignment; (3) ﬁne alignment.

3.2.1 Pre-Alignment

Before starting the registration process, an initial so-

lution is required. Instead of using a random solution

to start our method, we choose the best one among

three pre-alignments, which are: (a) center of mass;

(b) nose tip; (c) bounding box center — to avoid in-

correct nose tip localization due to noise points, this

landmark is deﬁned as the center of the closest 3 × 3

window to the sensor. In order to evaluate the conver-

gence behavior of each pre-alignment, few iterations

of the SA, only 75 based on our experiments, are per-

formed, using the cost function of the coarse align-

ment stage to guide the evaluation process. This eval-

uation is done to ﬁnd the pre-alignment that has the

fastest convergence. The selected pre-alignment rep-

resents a good starting point for the algorithm, which

can lead to a faster and better convergence.

3.2.2 Coarse Alignment

In this stage the SA-based searching procedure uses

MSAC (Torr and Zisserman, 2000) combined with

MSE of corresponding points between two images as

the cost function to obtain a coarse alignment. The

nearest-neighbor criterion is used to establish cor-

respondence between points of each image — the

search is performed using a KD-tree structure.

Based on a threshold applied on the associated er-

ror of corresponding points — in our case MSE is the

error measure — the MSAC classiﬁes corresponding

points either as inliers or outliers. The error associ-

ated to outliers is a ﬁxed penalty and to the inliers is

the error measure itself, squared. That means, they are

scored on how well they ﬁt the data (Torr and Zisser-

GNU Scientiﬁc Library - http://www.gnu.org/

software/gsl

HIERARCHICAL EVALUATION MODEL FOR 3D FACE RECOGNITION

man, 2000). The MSAC deﬁnition is given by Eq. 3.

) =



< T

≥ T

(3)

where e is the error of corresponding points and T is

the threshold.

By reducing the error associated to the outliers, we

minimize their inﬂuence on the registration process

and, therefore, a better alignment can be obtained.

In order to speed up this stage, only 3% of the

valid points are used. Our experiments have shown

that this sampling rate does not risk the coarse align-

ment.

The initial solution of this stage is the best so-

lution found in the iterations performed on the pre-

alignments of the previous stage. The “temperature”

of SA is reduced very slowly and only one itera-

tion is performed for each allowed “temperature” as

suggested by (Lundy and Mees, 1986). This stage

ends when no better solution is found within 350

consecutive iterations of SA, based on our experi-

ments this condition is a compromise between a good

coarse alignment and a small computing time. The

movements to neighbor solutions across each itera-

tion is done by the introduction of small random val-

ues within [−1,1] to each element of the transforma-

tion vector. The initial “temperature” was deﬁned as

= 0.002. At this “temperature” and using MSAC

as the cost function, approximately 60% of worse so-

lutions are accepted. According to (Rayward-Smith

et al., 1996) it is a criterion that should be met for

the initial “temperature”. The threshold value for

MSAC was empirically deﬁned as T = 0.7, which

represents an inlier boundary distance for the corre-

sponding points between images.

3.2.3 Fine Alignment

In this stage the cost function for the SA-based

searching procedure is the SIM calculated over 9% of

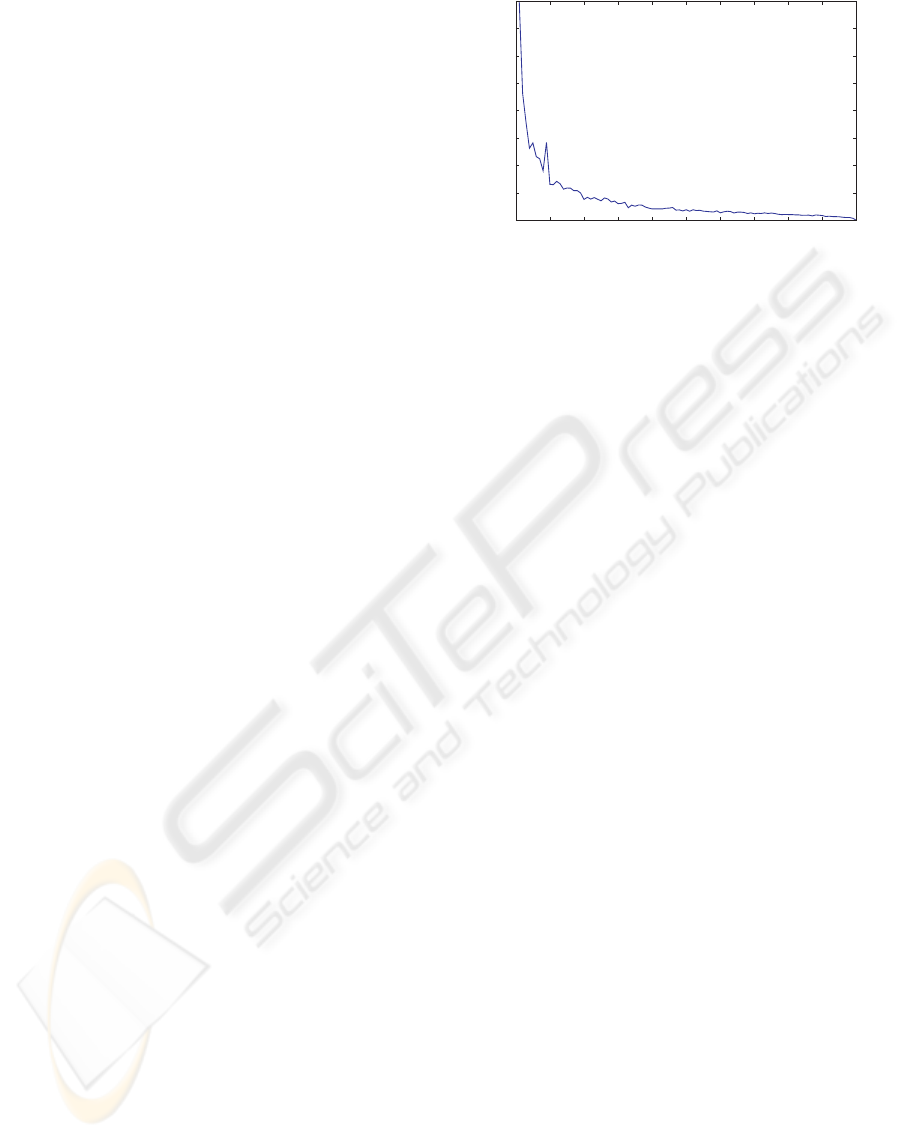
the image valid points. Our experiments, see Fig. 2,

have shown that SIM at this sampling rate, compar-

ing to SIM using all points, presents an average vari-

ation of approximately 2%. Therefore, the increase

of speed compensates the small inaccuracy. We have

used 200 face alignments to produce Fig. 2. For each

alignment it was calculated the relative error of SIM

using sampling rates varying from 1% to 99%, when

compared to SIM using all points.

The initial solution of this stage is the best solu-

tion found on the previous stage. Again, the cool-

ing schedule proposed by (Lundy and Mees, 1986)

was used. In an attempt to move to a better neigh-

bor solution, random values within [−0.0667,0.0667]

are introduced to each element of the transformation

0 10 20 30 40 50 60 70 80 90 100

DifferenceintheSIMvalue(%)

RelativeError

SamplingRate(%)

Figure 2: Relative error of SIM using a sampling rate when

compared to SIM using all points.

vector. These values are smaller than the ones in the

previous stage because a good alignment has already

been achieved and we only want to make minor move-

ments in order to improveit. The initial “temperature”

was deﬁned as t

= 0.15, again we have employed the

method suggested by (Rayward-Smith et al., 1996).

This stage ends when the solution is not improved

in 40 consecutive iterations of SA, as in the previ-

ous stage. This condition is a compromise between a

precise alignment and a small computing time.

4 HIERARCHICAL EVALUATION

MODEL AND FACIAL

REGIONS

We have used ﬁve facial regions (Fig. 3) in our hier-

archical evaluation model: nose region (NR), ellipti-

cal nose region (NE), circular nose region (NC), eyes

region (ER) and face region (FA). The three nose re-

gions were suggested in (Chang et al., 2006; Chang

et al., 2005) and are described to be relatively insensi-

tive to facial expressions. These three regions are also

important when using only neutral expression faces

because, even if a subject is asked to make a neutral

expression at two different times, the 3D face shape

will still be different by some amount (Chang et al.,

2006).

The hierarchical evaluation model, see Fig. 4, is

used in a veriﬁcation scenario. This model consists in

analyzing one region only when the matching score of

a previously analyzed one was not sufﬁcient to deter-

mine whether the images belong to the same subject

or not. The classiﬁcation of the images is based on

two thresholds: (1) a recognition threshold; (2) a re-

jection threshold. If the matching score is higher then

the recognition threshold, the images are assumed to

belong to the same subject (client), however if it is

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

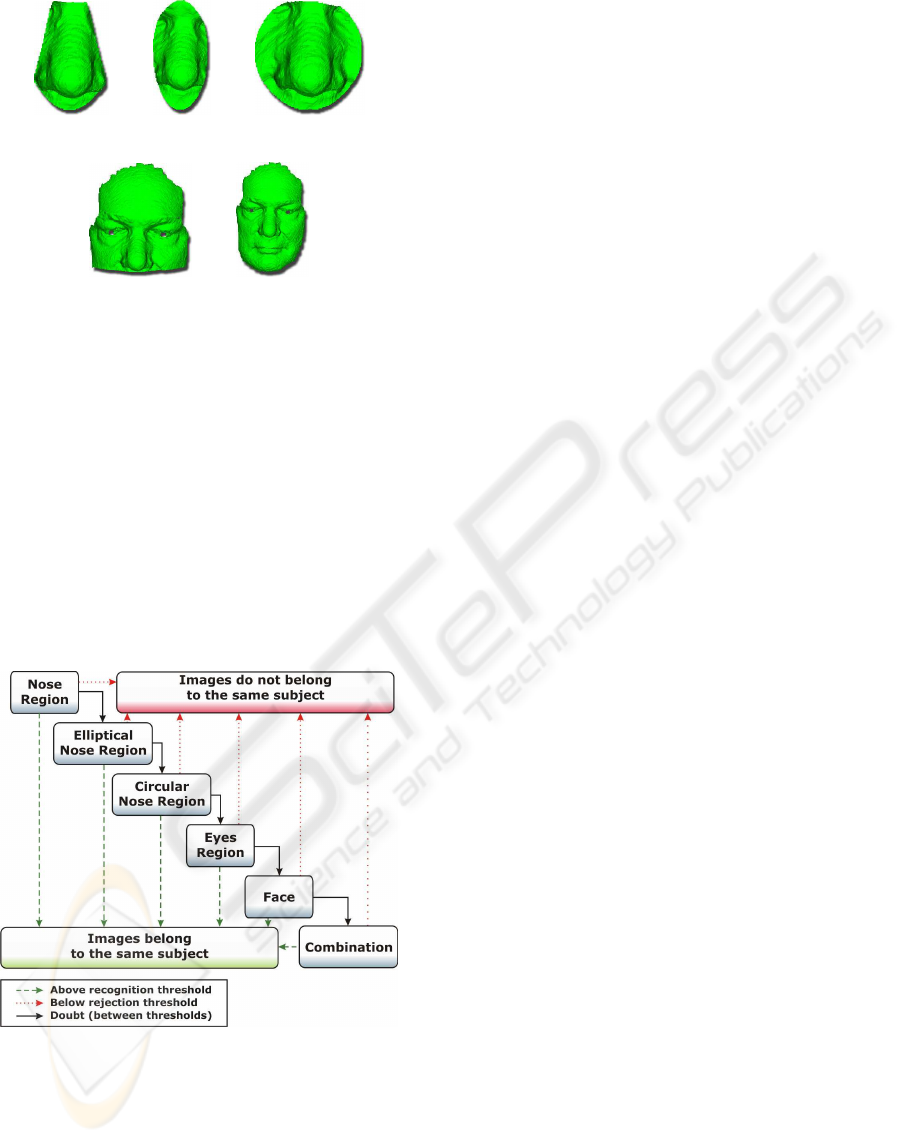
(a) NR (b) NE (c) NC

(d) ER (e) FA

Figure 3: Facial regions used in our evaluation model.

lower than the rejection threshold the images are la-

beled as belonging to different subjects (impostor).

In case the matching score lies between the thresh-

olds, no afﬁrmation can be made and the next region

of the hierarchy is used in another attempt to classify

the images. After obtaining all the matching scores,

the thresholds are automatically deﬁned in a way that

no client score is below the rejection threshold and

no impostor score is above the recognition threshold.

This model has two purposes: (1) achieve high veriﬁ-

cation rates; (2) keep a small execution time.

Figure 4: Proposed Hierarchical Evaluation Model.

Since the regions vary greatly in size, the order in

which they are evaluated plays a very important role

in keeping execution time as small as possible. The

execution goes from the smallest region, NR, to the

largest one, FA. By doing this, the average execution

time of the algorithm tends to be near the time neces-

sary to match the smaller regions. In the last level of

the hierarchy, the combination, which is a weighted

mean of the matching scores of previous levels, is

compared against a single threshold and the pair of

images is classiﬁed as client or impostor.

This model increases the veriﬁcation rate because

sometimes one single region can lead to the correct

result while the combination of all the regions cannot.

This particular situation can happen if one of the im-

ages has hair occlusion, noisy regions or expression.

5 EXPERIMENTAL RESULTS

The experiments were performed using 978 images

from the well-known FRGC v2.0 database (Phillips

et al., 2005). Each image of the database, acquired by

a Minolta Vivid 900/910 series sensor, has 640× 480

pixels and was divided according to the presence of

noise and expression. We have applied our approach

in the group that satisﬁes two criteria: (1) neutral

or minor expression; (2) little or no noise perturba-

tion from the acquisition process. This group con-

tains 978 images and it was used to establish a base-

line for our approach in a controlled environment.

We matched each image against all others, totalizing

477, 753 combinations (475, 091 from different sub-

jects and 2, 262 from the same subject). Using the

method proposed in (Segundo et al., 2007), each im-

age was automatically segmented into the ﬁve used

regions.

Fig. 5 presents ﬁve face matching where each im-

age was rendered using different colors to show the

interpenetrating areas. We can observe some partic-

ular cases, as in Fig. 5 (a) where the forehead is par-

tially occluded due to hair, or in Fig. 5 (p) where the

subject was using a bandannathat was not removedby

the segmentation algorithm. However, in both cases,

the SIM value for the alignment was enough for a cor-

rect classiﬁcation of the images.

By using the hierarchical evaluation model we

have achieved a veriﬁcation rate of 99.77% at a False

Acceptance Rate (FAR) of 0% which means that in

a veriﬁcation system, no impostor would be accepted

as a client. Table 1 presents the number of combina-

tions, rejection and recognition thresholds regarding

the execution of our evaluation model for the used

dataset. After the last threshold is applied, only 6

combinations out of 477,753 are misclassiﬁed and,

since we are using a FAR of 0%, the 6 combinations

are all false rejection cases. In Fig. 5 (u) – (y) it

is presented one case where the matching score was

not high enough for a correct classiﬁcation. Fig. 6

shows the variation of FAR and False Rejection Rate

(FRR) according to threshold variations. By analyz-

HIERARCHICAL EVALUATION MODEL FOR 3D FACE RECOGNITION

(a) A1 (b) A2 (c) A3 (d) A4 (e) A5

(f) B1 (g) B2 (h) B3 (i) B4 (j) B5

(k) C1 (l) C2 (m) C3 (n) C4 (o) C5

(p) D1 (q) D2 (r) D3 (s) D4 (t) D5

(u) E1 (v) E2 (w) E3 (x) E4 (y) E5

Figure 5: Examples of facial alignments obtained by our registration method: X1 and X2 are raw images from the database;

X3 is the rendered face segmentation of X1; X4 is the rendered face segmentation of X2; X5 is the alignment of X3 and X4;

(e) ﬁnal SIM value 41.38%; (j) ﬁnal SIM value 45.34%; (o) ﬁnal SIM value 47.11%; (t) ﬁnal SIM value 22.34%; (y) ﬁnal

SIM value 8.54%.

ing this ﬁgure we can see that the overlapping area of

the curves is very small, indicating that the scores of

clients and impostors are rarely mixed up.

Fig. 7 shows the Receiver Operating

Characteristic (ROC) curve, which demonstrates

the trade-off between the FAR and the FRR. We can

see that with such rates, in a veriﬁcation scenario the

system would have either secure (small FAR) and

convenient (small FRR) behavior. In Figs. 6 (b) and 7

we can see the point at which FAR equals FRR, this

point is called EER and, it is approximately 0.033%

for our approach.

For the assessment of the algorithm in a recogni-

tion scenario, the images were randomly divided into

three sets: one gallery and two probes. The gallery

set contains 256 images, one for each subject in the

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

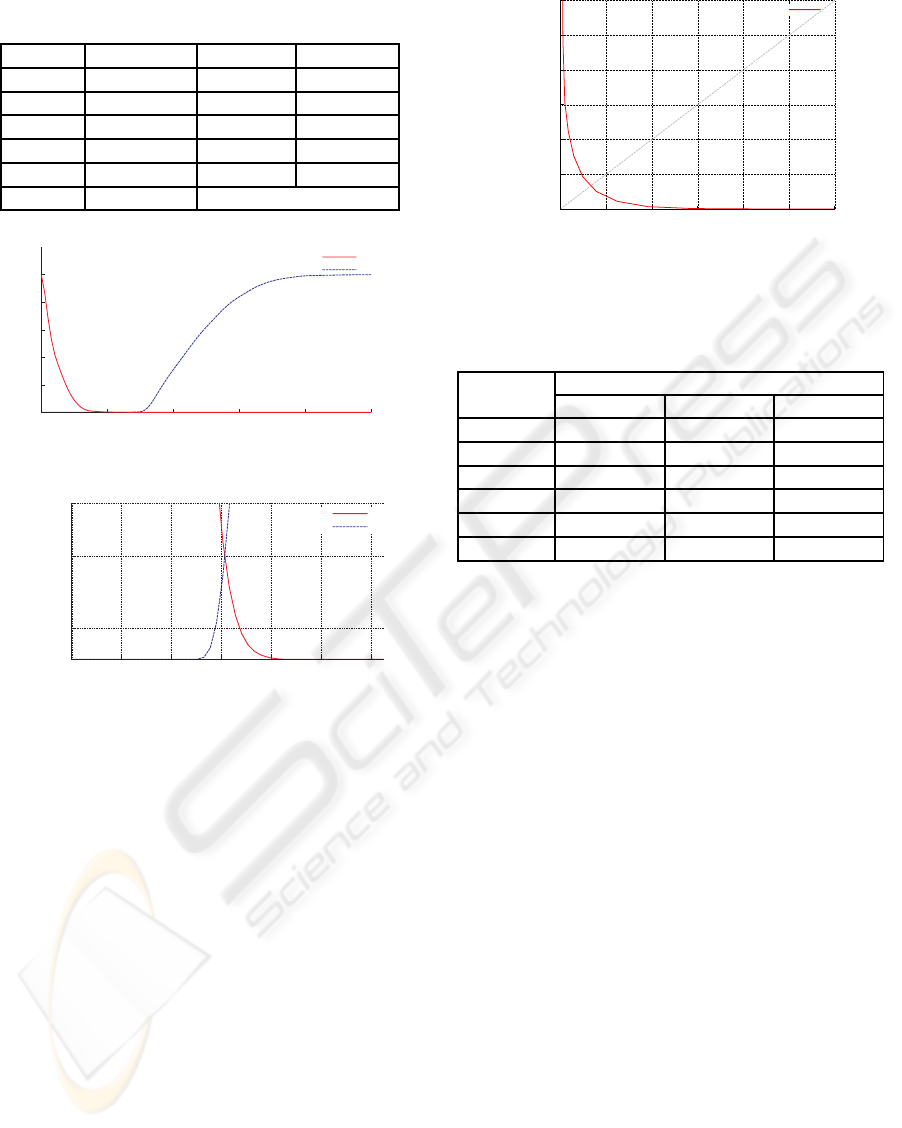
Table 1: Hierarchical evaluation using the ﬁve segmenta-

tions and their combination.

Region Nr. Comb. Rejec. T. Recog. T.

NR 477, 753 1.32% 29.60%

NE 427, 505 0.82% 24.43%

NC 412, 398 2.73% 23.31%

ER 253, 642 5.94% 14.10%

FA 11,469 4.48% 10.09%

Comb. 5,102 11.71%

0.0

0.2

0.4

0.6

0.8

1.0

0 20 40 60 80 100

Threshold

FAR

FRR

(a)

0.00010

0.00033

0.00050

0 8 16 24 32 40 48

Threshold

FAR

FRR

(b)

Figure 6: FAR and FRR curves: (a) FAR and FRR curves

for all possible thresholds; (b) approximation of the cross-

ing region.

database, and each probe set contains 361 images. By

combining the results for each region, in the same

way it was done for the veriﬁcation scenario, we have

reached a rank-one recognition rate of 100%. The

rank-one recognition rate and the Cumulative Match

Characteristic (CMC) curves for each facial region

and their combination are given in Table 2 and Fig. 8,

respectively.

6 CONCLUSIONS AND FUTURE

WORK

We have presented a robust approach for 3D face

matching based on SA, SIM and a hierarchical eval-

uation model. We propose the use of a precise reg-

0.0000

0.0005

0.0010

0.0015

0.0020

0.0025

0.0030

0.0000 0.0005 0.0010 0.0015 0.0020 0.0025 0.0030

FRR

FAR

ROC

Figure 7: Receiver Operating Characteristic curve.

Table 2: Rank-one recognition rate for each individual re-

gion and their combination.

Region

Rank-One Recognition Rate

Probe 1 Probe 2 Average

NR 95.29% 97.78% 96.53%

NE 98.33% 98.61% 98.47%

NC 98.33% 98.89% 98.61%

ER 99.72% 99.44% 99.58%

FA 98.89% 99.16% 99.03%

Comb. 100.00% 100.00% 100.00%

istration method and the SIM as a matching score to

verify similarity between face regions. The registra-

tion follows a coarse-to-ﬁne strategy, ﬁrst employing

the MSE constrained by the MSAC as the cost func-

tion of SA and then, the SIM as the cost function in

order to obtain a reﬁned alignment. The adopted eval-

uation model aims to minimize the execution time and

to maximize the veriﬁcation rate.

The experimental results have shown the effec-

tiveness of our approach for both recognition and

veriﬁcation scenarios. For the recognition problem,

our approach achieved a rank-one recognition rate of

100%. The rates for the veriﬁcation scenario are also

very high, 99.77% for the veriﬁcation rate at a FAR

of 0% and approximately 0.033% for the EER.

As a future work we plan to study the effects of

facial expressions on the proposed approach and, if

necessary, employ techniques that minimize them.

ACKNOWLEDGEMENTS

The authors would like to thank Dr. Jonathon Phillips

and Dr. Patrick Flynn for allowing us to use the

images; and Conselho Nacional de Desenvolvimento

Cient´ıﬁco e Tecnol´ogico (CNPq) for ﬁnancial sup-

port.

HIERARCHICAL EVALUATION MODEL FOR 3D FACE RECOGNITION

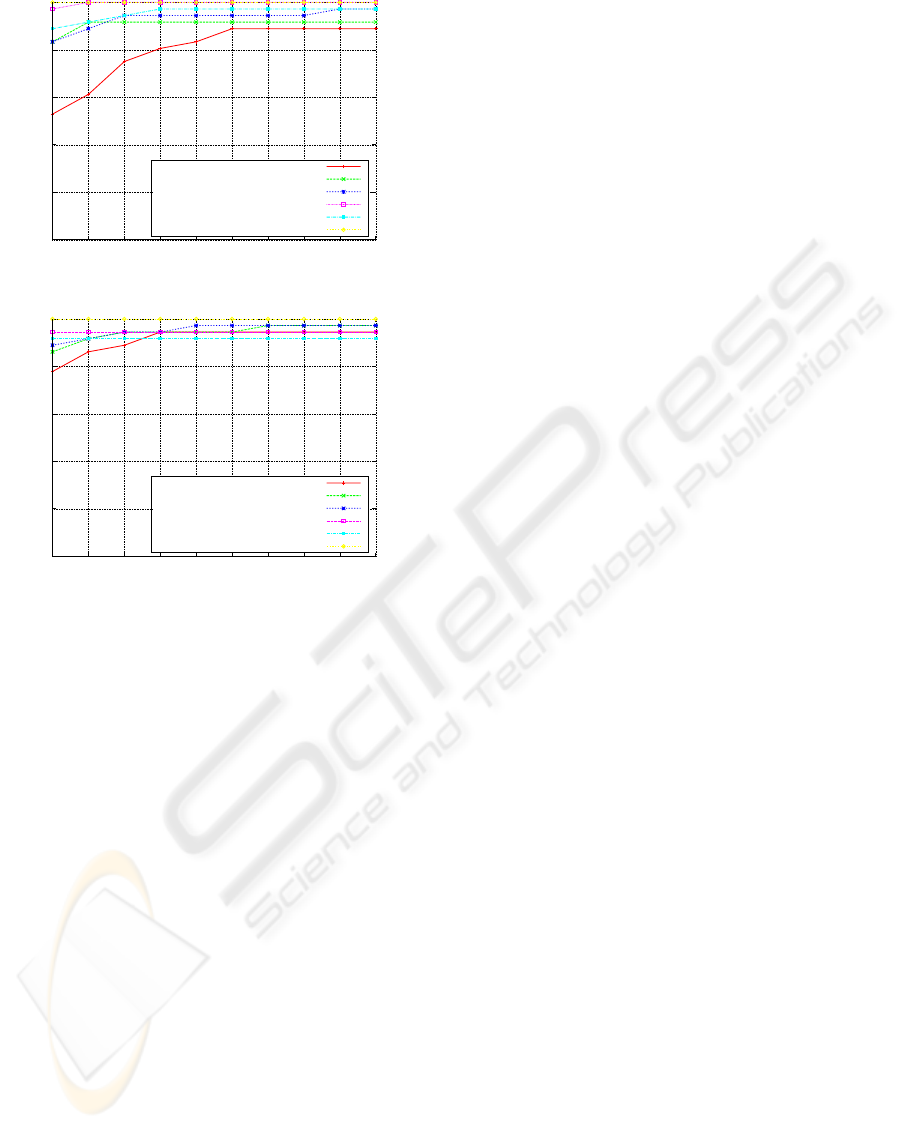
0.90

0.92

0.94

0.96

0.98

1.00

1 2 3 4 5 6 7 8 9 10

Nose Region

Elliptical Nose Region

Circular Nose Region

Eyes Region

Face

Combination

(a) CMC curves for probe 1

0.90

0.92

0.94

0.96

0.98

1.00

1 2 3 4 5 6 7 8 9 10

Nose Region

Elliptical Nose Region

Circular Nose Region

Eyes Region

Face

Combination

(b) CMC curves for probe 2

Figure 8: Cumulative Match Characteristic curves for each

region and their combination: (a) for probe set 1; (b) for

probe set 2.

REFERENCES

Bellon, O. R. P., Silva, L., Queirolo, C., Drovetto, S., and

Pamplona, M. (2006). 3d face image registration for

face matching guided by the surface interpenetration

measure. In ICIP, pages 2661–2664. IEEE.

Bellon, O. R. P., Silva, L., and Queirolo, C. C. (2005). 3D

face matching using the surface interpenetration mea-

sure. In Lecture Notes in Computer Science, volume

3617, pages 1051–1058. Springer-Verlag.

Besl, P. J. and McKay, N. D. (1992). A method for registra-

tion of 3-D shapes. IEEE Trans. Pattern Analysis and

Machine Intelligence, 14(2):239–256.

Chang, K. I., Bowyer, K. W., and Flynn, P. J. (2005). Adap-

tive rigid multi-region selection for handling expres-

sion variation in 3D face recognition. In Proc. of IEEE

Conf. CVPR, volume 3, pages 157–164.

Chang, K. I., Bowyer, K. W., and Flynn, P. J. (2006). Multi-

ple nose region matching for 3d face recognition under

varying facial expression. IEEE Trans. Pattern Anal-

ysis and Machine Intelligence, 28(10):1695–1700.

Chen, Y. and Medioni, G. (1992). Object modelling by reg-

istration of multiple range images. Image Vision Com-

puting, 10(3):145–155.

Gelfand, N., Ikemoto, L., Rusinkiewicz, S., and Levoy, M.

(2003). Geometrically stable sampling for the ICP

algorithm. In Proc. of 4th Intl. Conf. on 3D Digital

Imaging and Modeling, pages 260–267.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983).

Optimization by simulated annealing. Science,

220(4598):671–680.

Kittler, J., Hatef, M., Duin, R. P. W., and Matas, J. (1998).

On combining classiﬁers. IEEE Trans. Pattern Analy-

sis and Machine Intelligence, 20(3):226–239.

Lu, X. and Jain, A. K. (2005). Integrating range and texture

information for 3d face recognition. In Proc. of 7th

IEEE Workshop on Applications of Computer Vision,

pages 156–163.

Lu, X., Jain, A. K., and Colbry, D. (2006). Matching 2.5D

face scans to 3D models. IEEE Trans. Pattern Analy-

sis and Machine Intelligence, 28(1):31–43.

Lundy, M. and Mees, A. (1986). Convergence of an anneal-

ing algorithm. Mathematical Programming: Series A

and B, 34(1):111–124.

Phillips, P. J., Flynn, P. J., Scruggs, W. T., Bowyer, K. W.,

Chang, J., Hoffman, K., Marques, J., Min, J., and

Worek, W. J. (2005). Overview of the face recogni-

tion grand challenge. In Proc. of IEEE CVPR, pages

947–954.

Rayward-Smith, V. J., Osman, I. H., Reeves, C. R., and

Smith, G. D. (1996). Modern Heuristic Search Meth-

ods. John Wiley & Sons Ltd.

Rusinkiewicz, S. and Levoy, M. (2001). Efﬁcient variants

of the ICP algorithm. In Proc. of 3rd Intl. Conf. on 3D

Digital Imaging and Modeling, pages 145–152.

Segundo, M. P., Queirolo, C. C., Bellon, O. R. P., and Silva,

L. (2007). Automatic 3d facial segmentation and land-

mark detection. XIV Intl. Conf. on Image Analysis and

Processing, pages 431–436.

Silva, L., Bellon, O. R. P., and Boyer, K. L. (2005a). Pre-

cision range image registration using a robust surface

interpenetration measure and enhanced genetic algo-

rithms. IEEE Trans. Pattern Analysis and Machine

Intelligence, 27:762–776.

Silva, L., Bellon, O. R. P., and Boyer, K. L. (2005b). Ro-

bust Range Image Registration Using Genetic Algo-

rithms and the Surface Interpenetration Measure, vol-

ume 60 of Machine Perception and Artiﬁcial Intelli-

gence. World Scientiﬁc Publishing.

Torr, P. H. S. and Zisserman, A. (2000). MLESAC: A new

robust estimator with application to estimating image

geometry. CVIU, 78:138–156.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications