COLOR QUANTIZATION BY MORPHOLOGICAL HISTOGRAM
PROCESSING
Franklin C´esar Flores
Department of Informatics, State University of Maring´a, Maring´a, Brazil
Leonardo Bespalhuk Facci
Department of Informatics, State University of Maring´a, Maring´a, Brazil
Roberto de Alencar Lotufo
School of Electrical and Computer Engineering, State University of Campinas, Campinas, Brazil
Keywords:
Color quantization, Morphological histogram processing, Watershed transform.
Abstract:
In a previous paper it was proposed a graylevel quantization method by morphological histogram processing.
This paper introduces the extension of that quantization method to color images. Considering an image under
the RGB color space model, this extension reduces the number of colors in the image by partitioning an 3-D
histogram, similar to the RGB color space, in rectangular parallelepiped regions, through a iterative process.
Such partitioning is done, in each iteration, by application of the graylevel quantization method to the longest
dimension of the current region which has the greatest volume. The final classified color space is used to
quantize the image. This paper also shows the comparison of the proposed method to the classical median cut
one.
1 INTRODUCTION
Color reduction techniques are fundamental in dig-
ital image processing and computer graphics. Im-
age quantization by color reduction (Gonzalez and
Woods, 1992; Heckbert, 1982; Soille, 1996) has
been applied to solve problems of image display, im-
age compression, image simplification and segmenta-
tion. (Gomes and Velho, 1994).
Color quantization also provides the reduction of
flat zones (connected regions of pixels with constant
color) in the image, such a connected filter (Crespo
et al., 1997; Salembier and Serra, 1995; Heijmans,
1999; Meyer, 1998). The reduction of flat zones does
not introduct borders in the image, but, by supress-
ing some borders, two of more flat zones may be
joined in one. Flat zone reduction is usually applied to
image compression, image segmentation (Meyer and
Beucher, 1990; Beucher and Meyer, 1992) and in the
reduction of the statistics in an image in order to sim-
plify the number of samples used in pattern recogni-
tion techniques (Hirata Jr. et al., 1999; Flores et al.,
2000; Flores et al., 2002).
In a previous paper (Flores and Lotufo, 2001), it
was proposed a method which givesnot only an image
simplification in terms of graylevel reduction but also
in terms of flat zone reduction. The proposed method
is given by application of a set of morphological op-
erators to the image histogram. The main motivation
behind the project of this operator is that each object
in the image has a significative graylevel distribution.
So, to simplify an object in the image, that is enough
to classify its corresponding distribution in the his-
togram.
In that paper it was also proposed a method to re-
duce an image to n graylevels. It consists in to choose
n regional maxima in the processed histogram and
to filter the other peaks. The chosen maxima will
provide the classification of the graylevels in the his-
togram by application of watershed operator. The ma-
jor drawback of the method proposed in (Flores and
Lotufo, 2001) is the choice of the n regional maxima.
In that paper, the chosen regional maxima was the n
highest ones. Note that, by far, it is not the best crite-
rion to choose the regional maxima.
In a following paper (Flores et al., 2006), it
93
Flores F., Bespalhuk Facci L. and de Alencar Lotufo R. (2008).
COLOR QUANTIZATION BY MORPHOLOGICAL HISTOGRAM PROCESSING.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 93-100
DOI: 10.5220/0001088400930100
Copyright
c
 SciTePress

was proposed the application of dynamics (Grimaud,
1992) to select the regional maxima in order to
achieve a better graylevel reduction. Dynamics con-
sists in a valuation of extrema of the image by a mea-
sure of contrast that does not consider the size or
shape of valleys and peaks. It is usually applied to find
markers to morphological segmentation and achieve
hierarchical segmentation (Meyer, 1996). The results
achieved by the application of dynamics as regional
maxima criterion showed itselt far better than the sim-
ple choice of the highest peaks. Both, the visual qual-
ity of the resulting images and the flat zones reduction
are better when dynamics is applied.
This paper introduces the extension of the quan-
tization method by morphological histogram process-
ing to color images. Considering an image under the
RGB color space model, this extension reduces the
number of colors in the image to at most n colors by
partitioning the RGB color space in rectangular par-
allelepiped regions. Such partition is an iterative pro-
cess where, in each iteration, one region is split in at
most k rectangular parallelepiped regions. The split-
ting of a region is done by choosing the longest side
of the parallelepipe (one of the three dimensions, red,
green or blue), computing the histogram along this
side and applying the graylevel quantization method
to this histogram; the result gives where the region
must be split and how many regions are created in
that iteration.
This paper is organized as follows: section 2
presents some preliminar definitions used in this pa-
per. Section 3 introduces the color quantization
by morphological histogram processing. Section 4
presents some experimental results and section 5 con-
cludes this paper with a brief discussion.
2 DEFINITIONS
Let E ⊂ Z × Z be a rectangular finite subset of points.
Let K = [0, k] be a totally ordered set. Denote by
Fun[E, K] the set of all functions f : E → K. An im-
age is one of these functions (called graylevel func-
tions). Particularly, if K = [0, 1], f is a binary im-
age. An image operator (operator, for simplicity) is
a mapping ψ : Fun[E, K] → Fun[E, K].
Let N(x) be the set containing the neighbourhood
(Flores and Lotufo, 2001) of x, x ∈ E. We define a
path from x to y, x, y ∈ E as a sequence P(x, y) =
(p
0
, p
1
, ..., p
n
) from E, where p
0
= x, p
n
= y and
∀i ∈ [0, n − 1], p
i
∈ N(p
i+1
).
A connected subset of E is a subset X ⊂ E such
that, ∀x, y ∈ X, there is a path C entirely inside X.
Let f ∈ Fun[E, K]. A flat zone of f is a connected
subset X ⊂ E, such that f(x) = f(y), ∀x, y ∈ X.
Definition 1 The inf - reconstruction and sup - recon-
struction operators are given, respectively, by, ∀ f, g ∈
Fun[E, K],
ρ
B,g
( f) = δ
∞
B,g
( f)
ρ
∗
B,g
( f) = ε
∞
B,g
( f)
where B ⊂ E is the structuring element, n ∈ Z
+
and
δ
n
B,g
and ε
n
B,g
are, respectively, the n-conditional di-
lation and the n-conditional erosion operators (Heij-
mans, 1994). δ
∞
B,g
( f) (ε
∞
B,g
( f)) means that the dilation
(erosion) is applied till idempotency.
Let τ
i
: Fun[E, K] → Fun[E, [0, 1]], i ∈ K, be a
threshold function, where τ
i
( f)(x) = 1, if f(x) ≥ i,
and τ
i
( f)(x) = 0, otherwise.
Definition 2 Let f ∈ Fun[E, K]. A regional maxi-
mum is a flat zone Z such that f(z) > f(n), z ∈ Z,
n ∈ N, N ∈ F
Z
, where F
Z
is a set of all flat zones ad-
jacent to Z (Flores and Lotufo, 2001). The regional
maxima of f is found by application of a operator
µ
max
B
c
: Fun[E, K] → Fun[E, [0, 1]], given by
µ
max
B
c
( f) = τ
1
(ρ
B
c
,( f +1)
( f)) ∨ τ
k
( f)
where B
c
⊂ E is the structuring element defining con-
nectivity.
A regional miminum is a flat zone Z such that
f(z) < f(n), z ∈ Z, n ∈ N, N ∈ F
Z
, where F
Z
is a set
of all flat zones adjacent to Z.
2.1 Dynamics
Dynamics (Grimaud, 1992; Meyer, 1996) is a trans-
formation which valuates the extrema of an image ac-
cording to a contrast measurement. One advantage of
application of dynamics is that, while some methods
such as morphological filters need a size parameter to
evaluate constrast, the dynamics measurement does
not take in account the size and the shape of image
structures.
The evaluation of constrast of a regional minimum
is a good way to provide markers to application of
watershed operator in the morphological segmenta-
tion framework: an hierarchical segmentation may be
achieved by selecting the regional minima which dy-
namics is higher than a thresholding value and assign-
ing markers to them (Meyer, 1996).
Definition 3 Let x, y ∈ E. The dynamics Dyn
f
of a
path P(x, y) on an image f ∈ Fun[E, K] is given by,
Dyn
f
(P(x, y)) = {
_
| f(x
i
)− f(x
j
)| : x
i
, x
j
∈ P(x, y)}.
i.e., the dynamics of P(x, y) is given by the difference
in altitude between the points of highest and lowest
altitude of P(x,y).
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
94

Grimaud (Grimaud, 1992) also defines the dy-
namics between two points x, y ∈ E on an image
f ∈ Fun[E, K] as
Dyn
f
(x, y) = {
^
Dyn
f
(P(x, y)) : P(x, y), }
where P(x, y) is a path between x and y. However, it
will not be applied here, since the histogram is an 1-D
signal and, therefore, there is only one path between
any two points from the domain of histogram func-
tion. So, it will be considered here that Dyn
f
(x, y) =
Dyn
f
(P(x, y)).
Definition 4 Let a(Z) ∈ K be the altitude of a re-
gional minimum Z in f. The dynamics of Z is given
by,
Dyn(Z) = {
^
Dyn
f
(x, y), x ∈ Z, y ∈ M : a(M) < a(Z)}.
i.e., the dynamics of Z is given by the dynamics of the
path with the lowest dynamics that links Z to a point
y thats belongs to a catchment basin which regional
minimum has an altitude lower than Z.
Dynamics computation can be implemented by
using tree of critical lakes (Meyer, 1996) or based on
flooding simulations algorithms (Grimaud, 1992).
Given the dynamics of a regional minimum Z,
some metrics can be used to evaluate such minimum:
1. depth of the catchment basin which the minimum
is contained (given by the dynamics of the mini-
mum itself);
2. area of the catchment basin;
3. volume of the catchment basin;
Let us denote by Dyn
i
( f)(Z) the function that
computes to Z from f an value given by the metric
i ∈ {1, 2, 3} introduced above. Dyn
i
( f)(Z) will be
used to evaluate the significant distributions in the his-
togram, as will be explained below.
Note that two catchment basin which have the
same depth may have different volume or area mea-
surements. Classification of regional minima in an
image can be achieved by application of such metrics.
2.2 Graylevel Quantization by
Morphological Histogram
Processing
For a complete description of the graylevel quan-
tization by morphological histogram processing,
see (Flores et al., 2006; Flores and Lotufo, 2001). It
consists in an application of a set of morphological
operators to the image histogram. Since each object
in the image has a significative graylevel distribution,
that is enough to classify its corresponding distribu-
tions to simplify them.
Basically, the method computes all regional max-
ima in the histogram of the graylevel image and filters
all unnecessary regional maxima located in the signi-
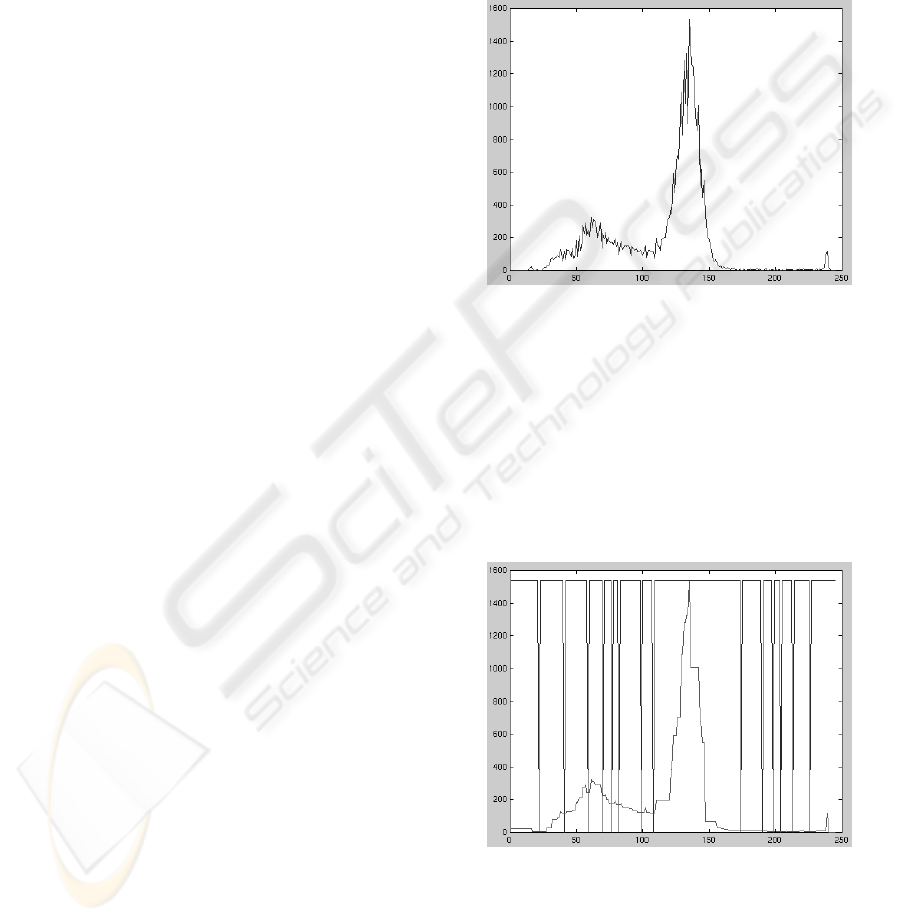
ficative distributions in the histogram (Fig. 2). The
filtered image is negated and the watershed operator
is applied, resulting in a pre-classification (Fig. 3).
Figure 1: Histogram.
Given an image with the regional maxima from
the filtered histogram (Fig. 1) labeled with their re-
spective graylevels. Its inf-reconstruction conditioned
to the pre-classification achieved by the watershed
operator gives classification of all graylevel classes
(Fig. 3). The classified histogram is used as a look-
up table in order to reduce the graylevels.
Figure 2: Pre-classification (filtered histogram and the wa-
tershed result).
As a consequence of such processing we have
a reduction in the graylevels appearing in the im-
age. In other words, the proposed filter is a mapping
ψ : Fun[E, K
1
] → Fun[E, K
2
], where |K
2
| < |K
1
|.
COLOR QUANTIZATION BY MORPHOLOGICAL HISTOGRAM PROCESSING
95

Figure 3: Classified graylevels.
2.3 The Use of Dynamics in Graylevel
Quantization by Morphological
Histogram Processing
When the operator ψ is applied to an image f , it re-
duces the graylevels appearing in f to the number of
regional maxima of the filtered histogram. However,
it is possible to reduce the graylevels to a smaller
number, by adding a parameter n which gives the
number of graylevels to appear in ψ( f). In this sub-
section we will present a way to select the n most sig-
nificant regional maxima of the filtered histogram by
application of dynamics.
We will denote by ψ
n
: Fun[E, K
1
] → Fun[E, K
2
],
|K
2
| < |K
1
|, |K
2
| = n, the operator which performs
the reduction of the graylevels in the image to n
graylevels.
Remember that the original histogram was filtered
in order to preserve the highest regional maximum
among a set of regiona maxima belonging to the same
distribution. Let h
f
and η(·) be, respectively, the orig-
inal and the filtered histograms.
Let D
i
: Fun[K, Z
+
] → Fun[K, Z
+
] be the function
given by,
D
i
(η)(x) =

Dyn
i
(ν(η))(Z) : x ∈ Z, if µ
max
B
(η)(x) = 1
0, otherwise
,
where ν is the negation operator and Z is one of the re-
gional minima of the negation of η(·). In other words,
if x belongs to a regional maximum in η(·), D
i
(η)(x)
will be equal to the dynamics (see section 2.1) of the
regional minimum where x is located in the negation
of η(·). i is the criterium chosen to evaluate η(·):
depth (1), area (2) or volume (3).
Let m be the number of regional maxima in η(·).
Let Q be the set defined by
Q = {q
i
∈ K : D
i
(η)(q
i
) > 0 and
D
i
(η)(q
i
) ≥ D
i
(η)(q
i+1
)), i = 1, ··· , m − 1}.
(i.e. Q is a sequence of all computed dynamics, ac-
cording to criterion i, in decreasing order).
Let σ
n
: Fun[K, Z
+
] × n → Fun[K, Z
+
] be the
mapping, given by, ∀x ∈ K, ∀n ∈ Z
+
,
σ
n
(x) =

max(h
f
), if x ∈ Q
0, otherwise
.
Let η
n
: Fun[K, Z
+
] × n → Fun[K, Z
+
] be the
mapping, given by, ∀x ∈ K, ∀n ∈ Z
+
,
η
n
= ν(ρ
∗
B,ν(η)
(σ
n
)).
By applying the operator η
n
, the n regional max-
ima of η(·) which have the highest dynamics are se-
lected. The function η
n
(·) contains just n regional
maxima and they are responsible for the classifica-
tion of n classes (given by application of watershed
operator). The remaining peaks are removed.
The method proposed in subsection 2.2 can be
now extended to reduce an image to n graylevels, by
adding the dynamics step introduced in this subsec-
tion to the framework, before the application of the
watershed operator.
3 THE PROPOSED METHOD
The color quantization method proposed in this paper
receives, as input data:
• The original image to be quantize (under the RGB
color space model);
• A positive integer n : the number of colors the
original image will be reduced to.
• A positive integer k : the maximum number of re-
gions a parallelepiped region will be split in each
iteration. If a region is split without the control
of this parameter, the splitting method may com-
pute many points and it may lead to the splitting
of many regions in a single iteration and to a bad
quantization result. With this parameter,no region
is split in more than k regions in a single iteration
(i.e., it is possible that the method finds less than
k splitting points in a iteration. If it is the case, the
method uses the points it found).
The starting parallelepiped region is a 3-D his-
togram from the original color image. This 3-D his-
togram is a discrete RGB color space cube, which di-
mensions are related, respectively, to red, green and
blue. Each color appearing in the original image has
a corresponding point inside this cube, and each point
stores how many pixels the color appears in the orig-
inal image. All other points in the cube are valued
zero.
Color quantization by morphological histogram
processing is the iterative process describe below:
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
96

1. Compute the starting region (the 3-D histogram
from the original image);
2. i ← 1 (the current number of regions);
3. Find, among the i current parallelepiped regions,
that one which have the greatest volume (let us
call it R
i
);
4. Take the longest dimension of the parallelepiped
region R
i
;
5. Let L
i
= [a
i
, b
i
] be the interval that defines the
longest dimension of R
i
;
6. For all l ∈ L
i
, let R
i
(l) be the slice of the region
that contains all the points projected in l (for in-
stance, if the longest dimension of R
i
corresponds
to the red band, R
i
(l) contains all points (l, x, y),
such that (l, x, y) ∈ R
i
);
7. Compute the 1-D histogram along the longest di-
mension of R
i
. The 1-D histogram h
i
: L
i
→ Z
+
is
given by, for all l ∈ L
i
,
h
i
(l) =
∑
x∈R
i
(l)
value(x),
where value(x) is the number of pixels that the
color x appears in the original image.
8. Apply the graylevel quantization by morpholog-
ical histogram processing to h
i
. Reduce it to, at
most, k classes. The choice of the k peaks is done
by computing the most significative volume dy-
namics. The classification of h
i
gives the points
where R
i
must be split. Let s be the number of
regions that R
i
will be split;
9. Split R
i
;
10. Let i ← i+ s− 1;
11. if i < n, go to Step 3.
Otherwise, stop.
The result of this algorithm is the classification
of the RGB color space model in at most n paral-
lelepiped regions. The color to be assigned to a region
is given by the centroid point of all color points that
belongs to the region.
The classified color space also works as a look-up
table. To quantize a color from the original image,
just check the region where the color belongs to and,
then, change the color by the one assigned to that re-
gion.
Figures 4 and 5 show the application of the color
quantization method to reduce Fig. 4 (a) to, respec-
tively, n = 64 and n = 16 colors. The original image
(Fig. 4 (a)) has 47915 distinct colors.
Figure 4 (b-c) shows the quantization to 64 colors
with parameter k = 2 and k = 4, respectively. The
visual result is a few better in Fig. 4 (b) than the result
shown in Fig. 4 (c).
The quantization of Fig. 4 (a) to 16 colors is shown
in Fig. 5. Figures 5 (b-e), show, respectively, the re-
sults achieved by the following choices of k: 2 (Fig. 5
(b)), 3 (Fig. 5 (c)), 4 (Fig. 5 (d)) and 5 (Fig. 5 (e)). In
this example, the lower the value of k, the better the
visual result.
There is a trade off in the choice of k: the lesser
the value, the better the visual result. However, the
greater the value of k, the faster the method converges
to the results. If there is no much difference in the
visual quality provided by several k values, as in the
case shown in Fig. 4, the higher values may be a good
choice.
4 EXPERIMENTAL RESULTS
The color quantization by morphological histogram
processing is, at a few points, similar to the median
cut algorithm (Heckbert, 1982), a classical quantiza-
tion method in computer graphics and image process-
ing context. Some experiments were done in order to
compare the color quantization method proposed in
this paper to the median cut one.
The results of each experiment will be assessed
qualitatively, by assessing the visual quality of the re-
sulting images, and quantitatively, by analyzing the
results of a quantization error function. The quantiza-
tion error function (Braquelaire and Brun, 1997) used
in this paper is given by,
E =
n
∑
i=1
∑
c∈C
i
f(c)


c− c
i


2
,
where n is the number of colors the image was quan-
tized to, C
i
is the set of colors in the original image
image converted to color c
i
, and f (c) is the number of
pixels in the image which color is c.
The goal in the first experiment is to reduce Fig. 6
(a) to n = 256 colors using the proposed method and
the median cut to assess the visual quality of the re-
sults provided by them. Figure 6 (a) has 89648 dis-
tinct colors and 288× 451 = 129888 pixels.
Figure 6 (b-c) show, respectively, the results pro-
vided by the color quantization by morphological his-
togram processing (using k = 5) and the median cut.
Both visual results are very good, but the result pro-
vided by the morphological method (Fig. 6 (b)) still
retained some small details from the original image.
The quantization errors computed to both quan-
tized images are very close to each other. The error
computed from the proposed method was 2.2968· 10
7
COLOR QUANTIZATION BY MORPHOLOGICAL HISTOGRAM PROCESSING
97

(a)
(b)
(c)
Figure 4: Reduction to n = 64 colors: (a) Original Image.
(b) k = 2. (c) k = 4.
(mean error of 176.8342 per pixel). The error com-
puted from the median cut image was 2.4003 · 10
7
(mean error of 184.8007 per pixel). The proposed
method achieved an error smaller than the achived by
the median cut one.
The second experiment consists in to reduce the
same original image (Fig. 6 (a)) to n = 16 colors using
the morphological method proposed in this paper and
the median cut technique. Again, the visual quality of
the results provided by them will be assessed.
The results provided by the color quantization by
morphological histogram processing (using k = 3)
(a)
(b)
(c)
(c)
Figure 5: Reduction to n = 16 colors: (a) k = 2. (b) k = 3.
(c) k = 4. (d) k = 5.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
98

(a)
(b)
(c)
Figure 6: Reduction to n = 256 colors: (a) Original Im-
age. (b) Color Quantization by Morphological Histogram
Processing (k = 5). (c) Median Cut.
and the median cut are shown, respectively, in Fig. 7
(a-b). Both methods present results with a strong loss
of quality in the visualization, but the result provided
by the quantization method proposed in this paper
(Fig. 7 (a)) has a visual quality far better than the pro-
vided by the median cut (Fig. 7 (b)).
The difference between the quantization errors is
more evident in this experiment. Quantization er-
ror computed from the proposed quantization method
was 1.4460·10
8
(mean error of 1113.2730 per pixel).
Median cut error was 2.2306 · 10
8
(mean error of
(a)
(b)
Figure 7: Reduction to n = 16 colors: (a) Color Quantiza-
tion by Morphological Histogram Processing (k = 3). (b)
Median Cut.
1717.3413 per pixel). In this experiment, the error
achieved by the proposed quantization method was
far lower than the error achieved by the median cut
method.
5 CONCLUSIONS
Color quantization by morphological histogram pro-
cessing, the extension of the graylevel processing pro-
posed in a previous paper, reduces the colors of an
image (under the RGB color space model) in a iter-
ative process where a 3-D histogram computed from
the image is split in at most n regions. This classi-
fied ”color space” is used as a look-up table to do the
image quantization.
The splitting of regions is an iterative process. In
each iteration, one region is split in at most k rect-
angular parallelepiped regions; it is done by choos-
ing the longest side of the parallelepipe region, com-
puting the histogram along this side and applying the
graylevel method to this histogram. It provides how
many regions are created in that iteration and where
the region must be split.
COLOR QUANTIZATION BY MORPHOLOGICAL HISTOGRAM PROCESSING
99

The method introduced in this paper depends on a
parameter k, that is the maximum number of regions
a parallelepipe will be split in each iteration. The de-
pendence of the parameter k is a drawback of the pro-
posed method and some way to impose an automatic
k value should be studied. Some quantization results
using several k values are shown and discussed in the
paper.
Experiments were done in order to compare the
quantization method proposed in this paper with the
classical median cut technique. In the first experi-
ment, both methods provided good visual quality re-
sults but the morphological methods still retained a
few details from the original image. The second ex-
periment showed a strong loss of information in the
application of both methods, but the color quantiza-
tion introduced in this paper provided a better visual
result. More, quantitative analysis was done in both
experiments and the quantization error given by the
application of the proposed quantization method was
lower than the error given by the median cut one.
Future works include the choice of new criteria to
choose the most significant peaks in the filtered his-
togram and the automatic choice of the k parameter.
ACKNOWLEDGEMENTS
First author is on leave from State University of Mar-
ing´a for doctorate purposes at School of Electrical and
Computer Engineering, State University of Camp-
inas, Brazil.
REFERENCES
Beucher, S. and Meyer, F. (1992). Mathematical Morphol-
ogy in Image Processing, chapter 12. The Morpholog-
ical Approach to Segmentation: The Watershed Trans-
formation, pages 433–481. Marcel Dekker.
Braquelaire, J. and Brun, L. (1997). Comparison and op-
timization of methods of color image quantization.
IEEE Transactions on Image Processing, 6(7):1048–
1051.
Crespo, J., Schafer, R. W., Serra, J., Gratind, C., and Meyer,
F. (1997). The flat zone approach: A general low-level
region merging segmentation method. Signal Process-
ing, 62(1):37–60.
Flores, F. C., Facci, L. B., and Lotufo, R. A. (2006). The
Use of Dynamics in Graylevel Quantization by Mor-
phologival Histogram Processing. In Proceedings
of 1st. International Conference on Computer Vision
Theory and Applications - Visapp 2006, pages 121–
130, Setubal, Portugal.
Flores, F. C., Hirata Jr., R., Barrera, J., Lotufo, R. A., and
Meyer, F. (2000). Morphological Operators for Seg-
mentation of Color Sequences. In IEEE Proceedings
of SIBGRAPI’2000, pages 300–307, Gramado, Brazil.
Flores, F. C. and Lotufo, R. A. (2001). Connected Filtering
by Graylevel Classification Through Morphological
Histogram Processing. In IEEE Proceedings of SIB-
GRAPI’2001, pages 120–127, Florianopolis, Brazil.
Flores, F. C., Peres, S. M., and Von Zuben, F. J. (2002).
Automatic Design of W-Operators using LVQ: Ap-
plication to Morphological Image Segmentation. In
IEEE Proceedings of International Joint Conference
on Neural Networks (IJCNN2002), pages 1930–1935,
Honolulu, Hawaii.
Gomes, J. and Velho, L. (1994). Computac¸ ˜ao Gr´afica :
Imagem. IMPA/SBM, Boston.
Gonzalez, R. C. and Woods, R. E. (1992). Digital Image
Processing. Addison-Wesley Publishing Company.
Grimaud, M. (1992). A New Measure of Contrast: the
Dynamics. In SPIE, editor, Image Algebra and Mor-
phological Image Processing III, volume 1769, pages
292–305.
Heckbert, P. (1982). Color Image Quantization for Frame
Buffer Display. Computer Graphics, pages 297–307.
Heijmans, H. J. A. M. (1994). Morphological Image Oper-
ators. Academic Press, Boston.
Heijmans, H. J. A. M. (1999). Introduction to Connected
Operators. In Dougherty, E. R. and Astola, J. T., ed-
itors, Nonlinear Filters for Image Processing, pages
207–235. SPIE–The International Society for Optical
Engineering,.
Hirata Jr., R., Barrera, J., Flores, F. C., and Lotufo, R. A.
(1999). Automatic Design of Morphological Opera-
tors for Motion Segmentation. In Stolfi, J. and Tozzi,
C. L., editors, IEEE Proc. of Sibgrapi’99, pages 283–
292, Campinas, SP, Brazil.
Meyer, F. (1996). The Dynamics of Minima and Contours.
In P. Maragos, R. S. Butt, M., editor, ISMM 3rd. Com-
putational Imaging and Vision, pages 329–336.
Meyer, F. (1998). From Connected Operators to Levelings.
In Heijmans, H. and Roerdink, J., editors, Mathemat-
ical Morphology and its Applications to Image and
Signal Processing, Proc. ISMM’98, pages 191–198.
Kluwer Academic Publishers.
Meyer, F. and Beucher, S. (1990). Morphological Segmen-
tation. Journal of Visual Communication and Image
Representation, 1(1):21–46.
Salembier, P. and Serra, J. (1995). Flat Zones Filtering,
Connected Operators, and Filters by Reconstruction.
IEEE Transactions on Image Processing, 4(8):1153–
1160.
Soille, P. (1996). Morphological Partitioning of Multiespec-
tral Images. Electronic Imaging, 5(3):252–265.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
100