
FACIAL EXPRESSION RECOGNITION USING ACTIVE
APPEARANCE MODELS
Pedro Martins, Joana Sampaio, Jorge Batista
∗
ISR-Institute of Systems and Robotics, Dep. of Electrical Engineering and Computers
FCTUC-University of Coimbra, Coimbra, Portugal
Keywords:
Active appearance models (AAM), Linear discriminant analysis (LDA), Facial expression recognition.
Abstract:
A framework for automatic facial expression recognition combining Active Appearance Model (AAM) and
Linear Discriminant Analysis (LDA) is proposed. Seven different expressions of several subjects, representing
the neutral face and the facial emotions of happiness, sadness, surprise, anger, fear and disgust were analysed.
The proposed solution starts by describing the human face by an AAM model, projecting the appearance
results to a Fisherspace using LDA to emphasize the different expression categories. Finaly the performed
classification is based on malahanobis distance.
1 INTRODUCTION
Facial expressions recognition plays an important role
in human communication since has more influence
than simpler audio information. Psychology studies
(T. Dalgleish, 1999) describe that there are six basic
emotions universally recognized: joy, sadness, sur-
prise, fear, anger and disgust. Notice that, these ex-
pressions are also compatible with MPEG-4 norm.
Clearly, in order to extract facial information from
one image we need to solve first the problem of find-
ing the face on it. Traditionally, there are two different
ways to approach this problem. Anthropometric fea-
ture extraction (Batista, 2007) based on detection of
facial characteristics such as eyes, eyebrows, mouth
and nose, or using appearance based methods. The
last one, is preferable since it is able to extract rel-
evant face information without background interfer-
ence and describes facial characteristics in a reduced
model. Our work on facial expressions recognition
belongs to the appearance based approaches.
Appearence-based face recognition involves im-
age preprocessing and the use of statiscal redundancy
reduction for compact coding. To synthesize a com-
plete image face, both shape and textute are modelled.
The AAM represents both shape and texture varia-
tions observed in a training image set and the corre-
lations between them. Supervised dimension reduc-
∗
This work was funded by FCT Project POSI/EEA-
SRI/61150/2004
tion use the knowledge of class structure and the use
of multi-linear models allow low-dimensional repre-
sentations which account for variations in geometry,
orientation and illumination.
In statistical supervised learning, Linear Discrim-
inant Analysis (Peter N. Belhumeur and Kriegman,
1997) is a classical solution that finds the basis vec-
tors maximizing the interclass distances while mini-
mizing the intraclass distances. Linear discriminant
analysis is performed in order to extract the most dis-
criminant features which maximizes class seperabil-
ity. The discriminating power of the appearance pa-
rameters (AAM) is analysed when projected in Fish-
erspace and the degree of similarity is measured in
that subspace using Mahalanobis distances. A series
of experiments where conducted on a set of unknown
images showing the faces of different subjects with
facial expressions ranging neutral to intensely expres-
sive.
This paper is organised as follows: section 2 gives
a brief introduction to the standard ActiveAppearance
Models (AAM) theory, section 3 describes the facial
recognition methodology used, section 4 shows ex-
perimental results and section 5 discusses the results.
123
Martins P., Sampaio J. and Batista J. (2008).
FACIAL EXPRESSION RECOGNITION USING ACTIVE APPEARANCE MODELS.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 123-129
DOI: 10.5220/0001088701230129
Copyright
c
SciTePress

2 ACTIVE APPEARANCE
MODELS
AAM is a statistical based segmentation method,
where the variability of shape and texture is captured
from the dataset. Building such a model allows the
generation of new instances with photorealistic qual-
ity. In the search phase the model is adjusted to
the target image by minimizing the texture residual.
For futher details refer to (T.F.Cootes and C.J.Taylor,
2001).
2.1 Shape Model
The shape is defined as the quality of a configuration
of points which is invariant under Euclidian Similar-
ity transformations (T.F.Cootes and C.J.Taylor, 2004).
This landmark points are selected to match borders,
vertices, profile points, corners or other features that
describe the shape.
The representation used for a single n-point shape
is a 2n vector given by:
x = (x
1
,y
1
,x
2
,y
2
,...,x
n−1
,y
n−1
,x
n
,y
n
)
T
(1)
With N shape annotations, follows a statistical
analysis where the shapes are previously aligned to a
common mean shape using a Generalised Procrustes
Analysis (GPA) removing location, scale and rotation
efects. Optionaly, we could project the shape distri-
bution into the tangent plane, but omitting this pro-
jection leads to very small changes (Stegmann and
Gomez, 2002).
Applying a Principal Components Analisys
(PCA), we can model the statistical variation with:
x = x+ Φ
s
b
s
(2)
where new shapes x, are synthesised by deforming
the mean shape, x, using a weighted linear combina-
tion of eigenvectors of the covariance matrix, Φ
s
. b
s
is a vector of shape parameters which represents the
weights. Φ
s
holds the t
s
most important eigenvectors
that explain a user defined variance.
2.2 Texture Model
For m pixels sampled, the texture is represented by
the vector:
g = [g
1
,g
2
,...,g
m−1
,g
m
]
T
(3)
Building a statistical texture model, requires
warping each training image so that the control points
match those of the mean shape. In order to prevent
holes, the texture mapping is performed using the re-
verse map with bilinear interpolation correction.
The texture mapping is performed, using a piece-
wise affine warp, i.e. partitioning the convex hull of
the mean shape by a set of triangles using the De-
launay triangulation. Each pixel inside a triangle is
mapped into the correspondent triangle in the mean
shape using barycentric coordinates, see figure 1.
(a) Original (b) Warped texture
Figure 1: Texture mapping example.
This procedure removes differences in texture due
shape changes, establishing a common texture refer-
ence frame.
To reduce the influence of global lighting variation
a scaling, α and offset, β is applied
g
norm
= (g
i
− β.1)/α (4)
After the normalization we get g
T
norm
.1 = 0 and
|g
norm
| = 1.
A texture model can be obtained by applying a
PCA on the normalized textures:
g = g+ Φ
g
b
g
(5)
where g is the synthesized texture, g is the mean
texture, Φ
g
contains the t
g
highest covariance texture
eigenvectors and b
g
is a vector of texture parameters.
Another possible solution to reduce the effects of
differences in ilumination is to perform a histogram
equalization independently in each of the three color
channels (G. Finlayson and Tian, 2005).
Similarly to shape analysis, PCA is conducted in
texture data to reduce dimensionality and data redun-
dacy. Since the number of dimensions is greater than
the number of samples (m >> N) it is used a low-
memory PCA.
2.3 Combined Model
The shape and texture from any training example is
described by the parameters b
s
and b
g
. To remove
correlations between shape and texture model param-
eters a third PCA is performed to the following data:
b =
W
s
b
s
b
g
=
W
s
Φ
T
s
(x− x)
Φ
T
g
(g−g)
(6)
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
124

where W
s
is a diagonal matrix of weights that
measures the unit difference between shape and tex-
ture parameters. A simple estimate for W
s
is to
weight uniformly with ratio, r, of the total variance
in texture and shape, i.e. r =
∑
i
λ
gi
/
∑
i
λ
si
. Then
W
s
= rI (Stegmann, 2000).
As result, using again a PCA, Φ
c
holds the t
c
high-
est eigen vectors, and we obtain the combined model.
b = Φ
c
c (7)
Due the linear nature for the model, is possible to
express shape, x, and texture, g, using the combined
model by:
x = x+ Φ
s
W
−1
s
Φ
c,s
c (8)
g = g+ Φ
g
Φ
c,g
c (9)
where
Φ
c
=
Φ
cs
Φ
cg
(10)
c is a vector of appearance controling both shape
and texture. One AAM instance is built by generating
the texture in the normalized frame using eq. 9 and
warping-it to the control points given by eq. 8. See
figure 2.
(a) Shape con-
trol points
(b) Texture
in normalized
frame
(c) AAM
instance
Figure 2: Building a AAM instance.
2.4 Model Training
An AAM search can be treated as an optimiza-
tion problem, where the texture difference between
a model instace and a target image is minimized,
|I
image
− I
model
|
2
updating the appearance parameters
c and pose.
Apparently, this could be a hard optimazation
problem, but we can learn how to solve this class of
ploblems, learning how the model behaves due pa-
rameters change, i.e. learning offline the relation be-
tween the texture residual and the correspondent pa-
rameters error.
Additionally, are considered the similarity param-
eters for represent the 2D pose. To mantain linear-
ity and keep the identity transformation at zero, these
pose parameters are redefined to: t = (s
x
,s
y
,t
x
,t
y
)
t
where s
x
= (scos(θ) − 1), s
y
= ssin(θ) represents a
combined scale, s, and rotation, θ. The remaining pa-
rameters t
x
and t
y
are the usual translations.
Now the complete model parameters, p, (a t
p
=
t
c
+ 4 vector) are given by:
p = (c
T
|t
T
)
T
(11)
The initial AAM formulation uses the multivariate
linear regression aproach over the set of training tex-
ture residuals, δg, and the correspondent model per-
tubations, δp. The goal is to get the optimal predition
matrix, in the least square sense, satisfying the linear
relation:
δp = Rδg (12)
Solving eq. 12 involves perform a set s experi-
ences, building the residuals matrices (P holds by col-
uns model parameters pertubations and G holds cor-
respondent texture residuals):
P = RG (13)
In AAM its safe to say that m >> t
s
> t
p
, so one
possible solution of eq. 13 can be obtained by Prin-
cipal Component Regression (PCR) projecting the
large matrix G into a k−dimensional subspace, where
k ≥ t
p
which captures the major part of the variation.
Later (T.F.Cootes and C.J.Taylor, 2001) it was
suggested a better method, computing the gradient
matrix
∂r
∂p
.
The texture residual vector is defined as:
r(p) = g
image
(p) − g
model
(p) (14)
whre the goal is to find the optimal update at
model parameters to minimize |r(p)|. A first order
Taylor expansion leads to
r(p+ δp) ≈ r(p) +
∂r(p)
∂p
δp (15)
minimizing, in the least square sense, eq. 15 gives
δp = −
∂r
∂p
T
∂r
∂p
T
!
−1
∂r
∂p
T
r(p) (16)
and
R =
∂r
∂p
†
(17)
FACIAL EXPRESSION RECOGNITION USING ACTIVE APPEARANCE MODELS
125

δp in eq. 16 gives the parameters probable update
to fit the model. Regard that, since the sampling is
always performed at the reference frame, the predi-
tion matrix, R, is considered fixed and it can be only
estimated once.
2.4.1 Pertubation Scheme
Table 1 shows the model pertubation scheme used in
the s experiences to compute R. The percentage val-
ues are refered to the reference shape.
Table 1: Pertubation scheme.
Parameter p
i
Perturbation δp
i
c
i
± 0.25σ
i
, ± 0.5σ
i
Scale 90%, 110%
θ ±5
o
, ±10
o
t
x
, t
y
± 5%, ± 10%
2.5 Iterative Model Refinement
For a given estimate p
0
, we used (P.Viola and Jones,
2004) method, the model can be fitted by
• Sample image at x → g
image
• Build an AAM instance AAM(p) → g
model
• Compute residual δg = g
image
− g
model
• Evaluate Error E
0
= |δg|
2
• Predict model displacements δp = Rδg
• Set k = 1
• Establish p
1
= p
0
− kδp
• If |δg
1
|
2
< E
0
accept p
1
• Else try k = 1.5,k = 0.5,k = 0.25,k = 0.125
this procedure is repeated until no improvement
is made to error |δg|. Figure 3 shows a successful
AAM search. Note that, as better the initial estimate
is, minor the risk of being trap in a local minimum.
3 FACIAL EXPRESSION
RECOGNITION
3.1 Linear Discriminant Analysis
The facial expression recognition procedure is per-
formed by firstly describing a set of faces using
the AAM model (Bouchra Abboud, 2004). After-
wards, each vector of appearance c is projected into
(a) 1
st
(b) 2
nd
(c) 3
rd
(d) 4
th
(e) 5
th
(f) 6
th
(g) Final (h) Original
Figure 3: Iterative model refinement.
Fisherspace, applying a Linear Discriminant Analy-
sis (LDA) (Peter N. Belhumeur and Kriegman, 1997).
This supervised learning technique consists in opti-
mizing the separability of the dataset observations ac-
cording to the expression class they belong to. This
is done by maximizing the between-class variance
while minimizing the within-class variance. These
variances are expressed by the two scatter matrixes
shown in eq. 18 and eq. 19.
S
b
=
n
c
∑
j=1
(µ
j
− µ)(µ
j
− µ)
T
(18)
S
w
=
n
c
∑
j=1
N
j
∑
i=1
(X
j
i
− µ
j
)(X
j
i
− µ
j
)
T
(19)
In these expressions, n
c
is the number of classes,
X
j
i
represents the i
th
sample of class j, and µ
j
and µ
are the mean of class j and the mean of all classes,
respectively. This linear transformation of data will
allow subsequent classification of new images repre-
senting one of the expression categories j.
3.2 LDA Evaluation Metric
Similary to a Principal Component Analysis, a LDA
transformation also involves performing an eigenvec-
tor decomposition which reflects the importance of
the data variance on the transformed subspace. The
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
126

resulting data model retains the features that maxi-
mize class separability while holding a percentage of
the data variance.
In order to evaluate the quality of the data discrim-
ination, we developed a metric based on applying a k-
means clustering algorithm on the result of the LDA.
Let us consider the ideal case where all the observa-
tions were completely separated after LDA. In this
case, we could apply a clustering algorithm on the
data and obtain n
c
groups containing all faces with
the same expression. Table 2 shows what would be
the ideal clustering result for a dataset of n
s
subjects
per expression. Note that since there are seven ex-
pressions the k-means algorithm would be applied to
get seven groups.
Table 2: k-means clustering result for ideal LDA.
1 2 3 4 5 6 7
Neut n
s
0 0 0 0 0 0
Happ 0 n
s
0 0 0 0 0
Sad 0 0 n
s
0 0 0 0
Surp 0 0 0 n
s
0 0 0
Ang 0 0 0 0 n
s
0 0
Fear 0 0 0 0 0 n
s
0
Disg 0 0 0 0 0 0 n
s
The metric assigns a discrimination quality value
to the clustering result. Its value is calculated by sum-
ming the difference between the higher and the lower
values of each row of this table (i.e. the sum of the
degree of concentration of each class). The higher
the metric output, the better is the discrimination. By
applying this metric to several LDA runs, with differ-
ent number of features retained, we can estimate how
many modes of variation should be hold to optimize
the discrimination.
3.3 Classification
Once defined the axes that maximize the data classes
separability, it is possible to classify either training
images or unseen faces. The classification for an un-
known face image consists in two steps. The first is
projecting its appearance vector, c, on the hiperspace
that resulted from the trainning process. The second
is to estimate to each group does this projected point
belongs to. In our case this is done by using an adap-
tation of the nearest-neighbourhood algorithm, which
takes in consideration not only the distance of the
point to the centre of each group, but also its disper-
sion. The distance to each group is measured using
malahanobis distance (Krzanowski, 1988), eq. 20,
since it gives a scaled measure of an instance from
a particular class.
D = (c− c
i
)Σ
−1
(c− c
i
) (20)
c
i
is the vector of extracted appearance parame-
ters, c
i
is the centroid of the class multivariate distri-
bution and Σ is the within-class covariance matrix.
4 EXPERIMENTAL RESULTS
For the purpose of this work, an expression database
was built. It consists in 21 individuals showing 7
different facial expressions each. These expressions
are: neutral expression, happiness, sadness, surprise,
anger, fear and disgust. The data set is therefore
formed by a total of 147 colour images (640× 480).
Figure 4 shows AAM model instances of a given sub-
ject for each one of the 7 facial expressions used.
(a)
Neutral
(b)
Happy
(c) Sad
(d)
Surprise
(e) Anger (f) Fear (g)
Disgust
Figure 4: AAM instances of facial expressions used.
The AAM shape model was built using 58 anno-
tated landmarks (N = 58). The texture model was
generated sampling around 47000 pixels using also
colour information (g = 141000). Table 3 shows the
different values for retained variance used in each of
the three PCA that are required to create the combined
model, as well as the combined variation modes for
each one of this values.
Table 3: Retained variance and correspondent number of
modes, t
c
.
Variance(%) t
c
95.0 17
97.0 29
98.0 42
99.0 70
99.5 97
99.9 133
To evaluate the classification results, a leave-one-
out cross-validation method was adopted. In this
FACIAL EXPRESSION RECOGNITION USING ACTIVE APPEARANCE MODELS
127
method each one of the dataset observations is used
once as the testing sample, while all the remaining
data is used for training.
4.1 First Experience - Optimizing AAM
and LDA variation Modes
In a first experiment we studied the influence of the
variation modes retained either during AAM con-
struction or during LDA on the classification perfor-
mance. On these experiment we used all the 147 im-
ages of the database. First we performed an evalua-
tion of the discrimination quality by varying the num-
ber of discrimination features retained on several face
models with different PCA variation modes retained.
As discrimination quality metric output depends on
the result of a k-means clustering, these tests were re-
peated for 250 times. A histogram of the best LDA
features retained in each trial was created for every
AAM model used. Figure 5 shows the result when
99.0% variation modes are retained on our dataset.
Figure 5: Histogram for best LDA modes on 250 trials.
As it can be seen, three or four LDA modes maxi-
mize the separation of classes. This was also observed
for 95.0% and 97.0% AAM variation modes.
Using these two values as LDA modes retained,
we performed leave-one-out cross-validation classi-
fication for face models with 95.0%, 97.0%, 98.0,
99.5% and 99.9% AAM modes. The global classi-
fication results are shown on figure 6.
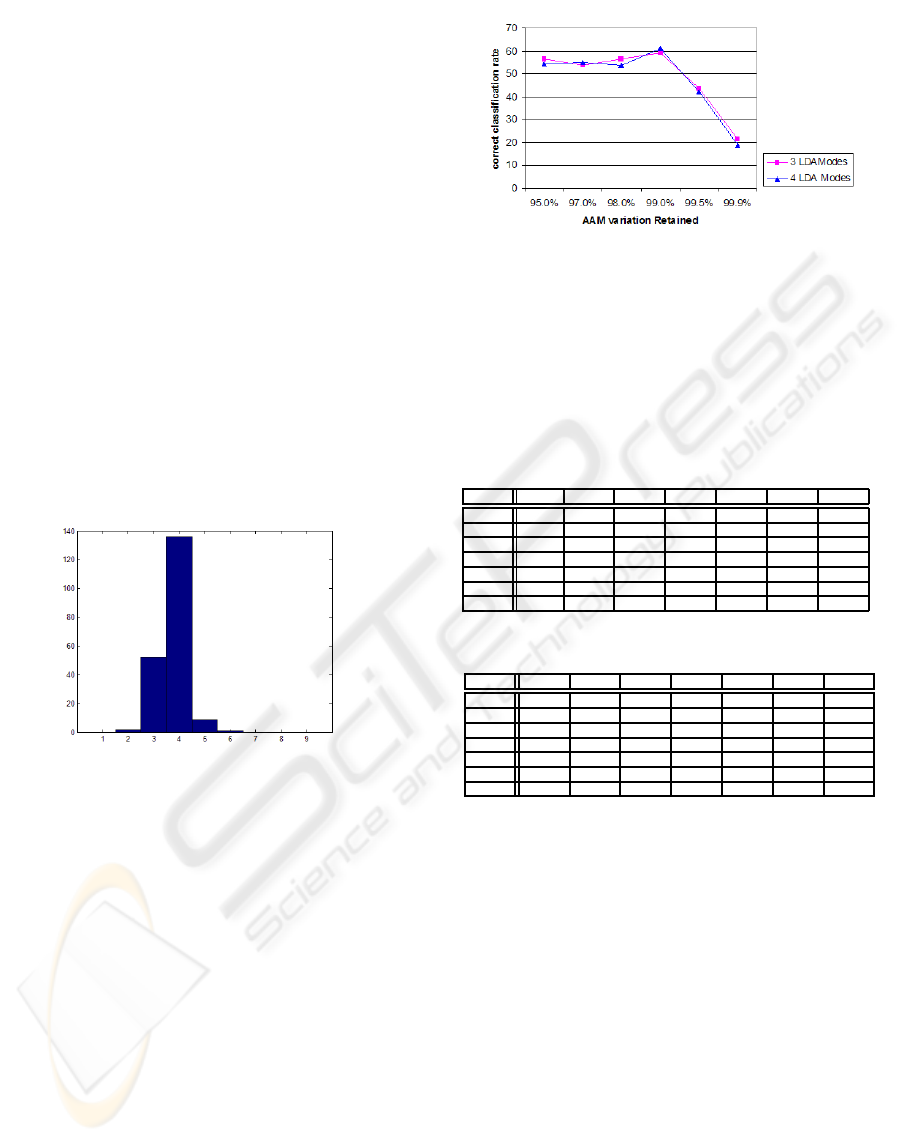
It is clear from this graph observation that the clas-
sification performance varies with the percentage of
variation retained on the AAM construction process.
The best global classifications results were obtained
for 99.0% of variance retained.
4.2 Second Experiment - 7 Expressions
On the second experiment we analyse the classifi-
cation performance for each expression. The same
dataset with 21 subjects in 7 different expressions is
Figure 6: Variation of global classification results with dif-
ferent number of AAM modes retained.
used and a confusion matrix is created that represent
the classification results for each expression. The re-
sults of the classification for all datasets are resumed
on tables 4, 5 and 6 for different values of retained
variance.
Table 4: Confusion Matrix 97.0% Overal recognition rate = 55%.
Neut Happ Sad Surp Ang Fear Disg
Neut 19.0 0 52.38 0 9.52 19.05 0
Happ 0 90.48 0 0 0 4.77 4.77
Sad 9.52 0 61.90 4.77 9.52 14.29 0
Surp 0 0 0 80.95 0 19.05 0
Ang 0 0 14.29 0 33.33 9.52 42.86
Fear 0 4.77 9.52 19.05 14.29 52.38 0
Disg 0 14.29 0 0 38.10 0 47.62
Table 5: Confusion Matrix 98.0% Overal recognition rate = 56.5%.
Neut Happ Sad Surp Ang Fear Disg
Neut 33.33 0 61.90 0 0 4.76 0
Happ 0 80.95 0 0 0 9.52 9.52
Sad 0 4.76 66.67 0 19.05 9.52 0
Surp 0 0 0 71.43 0 28.57 0
Ang 0 4.76 4.76 0 42.86 14.29 33.33
Fear 0 4.76 9.52 19.05 9.52 52.38 4.76
Disg 0 9.52 0 0 38.10 4.76 47.62
We can see from this results that there is an ef-
fect of confusion between neutral and sad expres-
sions, and also between anger and disgust. This sug-
estes that there is an appearance correlation between
these two pairs of expressions. In fact, these results
are not surprising. Several neuroscience (Killgore and
Yurgelun-Todd, 2003) studies have showned that in
case of human emotion recognition, to percieve sad
and anger expressions, an especific cognitive process
is required.
4.3 Third Experiment - 5 Expressions
Experiment three tries to eliminate the confusion ef-
fect described on the previous experiment. Faces ex-
pressing sadness and anger were excluded both from
training and testing. The results of the classification
for the same LDA and AAM conditions are expressed
on tables 7, 8 and 9.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
128

Table 6: Confusion Matrix 99.0% Overal recognition rate = 61.2%.
Neut Happ Sad Surp Ang Fear Disg
Neut 52.38 0 42.86 0 4.76 0 0
Happ 0 90.48 4.76 0 0 4.76 0
Sad 4.76 4.76 76.19 0 4.76 4.76 4.76
Surp 0 0 0 76.19 0 23.81 0
Ang 4.76 0 9.52 0 33.33 23.81 28.57
Fear 0 9.52 4.76 14.29 4.76 66.67 0
Disg 0 23.81 4.76 0 33.33 4.76 33.33
Table 7: Confusion Matrix 97.0% Overal recognition rate = 74.3%.
Neut Happ Surp Fear Disg
Neut 57.14 0 0 42.86 0
Happ 0 90.48 0 9.52 0
Surp 0 0 76.19 23.81 0
Fear 9.52 4.76 23.81 61.90 0
Disg 0 9.52 0 4.76 85.71
Table 8: Confusion Matrix 98.0% Overal recognition rate = 76.2%.
Neut Happ Surp Fear Disg
Neut 90.48 0 0 9.52 0
Happ 0 85.71 0 4.76 9.52
Surp 0 0 71.43 28.57 0
Fear 4.76 4.76 19.05 66.67 4.76
Disg 0 19.05 0 14.29 66.67
Table 9: Confusion Matrix 99.0% Overal recognition rate = 63.8%.
Neut Happ Surp Fear Disg
Neut 80.95 9.52 4.76 4.76 0
Happ 9.52 66.67 0 14.29 9.52
Surp 4.76 0 66.67 28.57 0
Fear 4.76 9.52 28.57 52.38 4.76
Disg 9.52 23.81 4.76 9.52 52.38
5 CONCLUSIONS
We used standart AAM model to discribe face entities
in a compact way. With LDA we are able to separate
the several emotion expression classes and perform
classification using mahalanobis distance.
On the AAM model building process, holding
more information on the appearance vectors not al-
ways results on a better discrimination result. In our
experiments, this value rounds 99.0% of variance re-
tained.
The number of LDA eigenvectors used is another
parameter of great importance. K-means is used in
order to give us a good estimation for this value.
As expected, the larger the number of expressions
used, the worse is the overal successful classification
rate. The reason for this is that there are correlations
between the two pairs of expressions neutral, sad and
anger, disgust, comproved by psico-physics studies.
We achieved, with all the seven expressions, an
overal successful recognition rate of 61.1%. Remov-
ing correlated expressions, this recognition rate in-
creases to a maximum of 76.2%.
REFERENCES
Batista, J. P. (2007). Locating facial features using an an-
thropometric face model for determining the gaze of.
faces in image sequences. ICIAR2007 - Image Analy-
sis and Recognition.
Bouchra Abboud, Frank Davoine, M. D. (2004). Facial
expression recognition and synthesis based on an ap-
pearance model. Signal Processing Image Communi-
cation.
G. Finlayson, S. Hordley, G. S. and Tian, G. Y. (2005). Il-
luminant and device invariant color using histogram
equalisation. Pattern Recognition.
Killgore, W. D. and Yurgelun-Todd, D. A. (2003). Acti-
vation of the amygdala and anterior cingulate during
nonconscious processing of sad versus happy faces.
NeuraImage.
Krzanowski, W. J. (1988). Principles of multivariate analy-
sis. Oxford University Press.
Peter N. Belhumeur, J. P. H. and Kriegman, D. J. (1997).
Eigenfaces vs. fisherfaces: Recognition using class
specific linear projection. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence.
P.Viola and Jones, M. (2004). Rapid object detection using
a boosted cascate of simple features. Proceeding of
the IEEE Conference on Computer Vision and Pattern
Recognition.
Stegmann, M. B. (2000). Active appearance models theory,
extensions & cases. Master’s thesis, IMM Technical
Univesity of Denmark.
Stegmann, M. B. and Gomez, D. D. (2002). A brief intro-
duction to statistical shape analysis. Technical report,
Informatics and Mathematical Modelling, Technical
Univesity of Denmark.
T. Dalgleish, M. P. (1999). Handbook of cognition and emo-
tion. John Wiley & Sons Ltd.
T.F.Cootes and C.J.Taylor (2004). Statistical models of ap-
pearance for computer vision. Technical report, Imag-
ing Science and Biomedical Engineering - University
of Manchester.
T.F.Cootes, G. E. and C.J.Taylor (2001). Active appearance
models. IEEE Transactions on Pattern Analysis and
Machine Intelligence.
FACIAL EXPRESSION RECOGNITION USING ACTIVE APPEARANCE MODELS
129
