A MINIMUM ENTROPY IMAGE DENOISING ALGORITHM
Minimizing Conditional Entropy in a New Adaptive Weighted K-th Nearest
Neighbor Framework for Image Denoising
Cesario Vincenzo Angelino, Eric Debreuve and Michel Barlaud
Laboratory I3S University of Nice-Sophia Antipolis/CNRS, 2000, route des Lucioles - 06903 Sophia Antipolis, France
Keywords:
Image denoising,variational methods, entropy, k-th nearest neighbors.
Abstract:
In this paper we address the image restoration problem in the variational framework. The focus is set on
denoising applications. Natural image statistics are consistent with a Markov random field (MRF) model
for the image structure. Thus in a restoration process attention must be paid to the spatial correlation between
adjacent pixels.The proposed approach minimizes the conditional entropy of a pixel knowing its neighborhood.
The estimation procedure of statistical properties of the image is carried out in a new adaptive weighted
k-th nearest neighbor (AWkNN) framework. Experimental results show the interest of such an approach.
Restoration quality is evaluated by means of the RMSE measure and the SSIM index, more adapted to the
human visual system.
1 INTRODUCTION
The goal of image restoration is to recover an im-
age that has been degraded by some stochastic pro-
cess. Research focus was set on removing additive,
independent, random noise. However, more general
degradation phenomenons can be modeled, such as
blurring, non-independent noise, and so on. When
the only degradation present in an image is noise, the
model is described by the equation
˜
X = X + N (1)
where
˜
X is the degraded image, X is the ideal image
and N is the additive noise term.
The literature in image restoration is vast and several
techniques have been proposed in different frame-
works such as linear and nonlinear filtering in either
the spatial or a transform domain. Nonlinear filtering
approaches are typically based on variational meth-
ods, leading to algorithm based on partial differential
equations. Indeed, these methods define an energy
functional based on geometric or statistical properties
of images. The minimization of this functional leads
to the correspondent partial differential equations or
evolution equation. A great deal of image process-
ing work developments are based on a stochastic
model of image structure given by Markov random
fields (MRFs) (Geman and Geman, 1990). Recent
researches (Huang and Mumford, 1999; Lee et al.,
2003; Carlsson et al., 2007) confirm that the statistics
of natural images are consistent with the MRF model
for the image structure, showing that a spatial corre-
lation between adjacent pixel exists. This correlation
must be take into account in the restoration process
to preserve the image structures. The idea is to con-
sider the intensity of a pixel jointly with the intensities
of its neighborhood. In particular the conditional en-
tropy of the pixel intensity knowing its neighborhood
is minimized (Awate and Whitaker, 2006). We use en-
tropy because it provides a measure of dispersion of
the random variable (Cover and Thomas, 1991) and
it is robust to the presence of outliers in the samples.
The underlying PDF can be estimated directly from
the data using a common nonparametric Parzen win-
dowing method. However Parzen methods presents
some drawbacks that can be avoided using the k-th
nearest neighbor (kNN) methods, as shown in sec-
tion 5. The experimental results show the slightly
better performance of the latter method with respect
to Parzen methods. The quality of restored images is
evaluated by the largely used RMSE measure and also
by means of the Structure Similarity (SSIM) measure
(Wang et al., 2004), more adapted to the human visual
system (HVS).
This paper is organized as follows. In section 2 the
energy and its derivative are presented and the adap-
tive weighted kNN framework is introduced. In sec-
tion 3 a high level overview of the algorithm is given
and in section 4 some experimental results are shown.
577
Vincenzo Angelino C., Debreuve E. and Barlaud M. (2008).
A MINIMUM ENTROPY IMAGE DENOISING ALGORITHM - Minimizing Conditional Entropy in a New Adaptive Weighted K-th Nearest Neighbor
Framework for Image Denoising.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 577-582
DOI: 10.5220/0001092605770582
Copyright
c
 SciTePress

Finally, discussion and future works are proposed in
the last section.
2 KNN RESTORATION
2.1 Image Model
Let us model the images as random field. A random
field is a family of random variables X(Ω;T) for some
index set T, where, for each fixed T = t, the random
variable is defined on the sample space Ω. If we fix
Ω = ω and let T be a set of points defined on a dis-
crete Cartesian grid, we have a realization of the ran-
dom field called the digital image, X(ω,T). In this
case, {t}
t∈T
is the set of pixels in the image. For two-
dimensional images, t is a two-vector. If we fix T = t,
and let ω vary, then X(t) is a random variable on the
sample space. We denote a specific realization X(ω;t)
(the intensity at pixel t) a deterministic function x(t).
If we associate with T a family of pixel neighbor-
hoods N = {N
t
}
t∈T
such that N
t
⊂ T, t /∈ N
t
, and
u ∈ N
t
if and only if t ∈ N
u
, then N is called a neigh-
borhood system for the set T. Points in N
t
are called
neighbors of t. We define a random vector Y(t) =
{X(t)}
t∈N
t
, corresponding to the set of intensities at
the neighbors of pixel t. We also define a random vec-
tor Z(t) = (X(t),Y(t)) to denote image regions, i.e.,
pixels combined with their neighborhoods.
2.2 Energy and Derivative
Image restoration is an inverse problem, that can be
formulated as a functional minimization problem. We
consider the conditional entropy functional, i.e., the
uncertainty of the random pixel X when its neighbor-
hood is given, as suitable measure for denoising ap-
plications (Awate and Whitaker, 2006). Thus the re-
covered image satisfies
X
∗
= argmin
X
h(
˜
X|
˜
Y = y
i
) (2)
Entropy functional can be approximated by the fol-
lowing estimator (Ahmad and Lin, 1976)
h(X|Y = y
i
) ≈ −
1
|T|
∑
t
j
∈T
log p(x
j
|y
i
), (3)
where
p(s|y
i
) =
1
|T
y
i
|
∑
t
m
∈T
y
i
K
h
(s− x
m
), (4)
is the Parzen kernel estimate of the PDF. T
y
i
is the set
of index pixels which have the same neighborhood y
i
.
In order to solve the optimization problem (2) a steep-
est descent algorithm is used. The energy derivative
of (3) is (see Appendix for the demonstration)
∂h(X|Y = y
i
)
∂x
i
= −
1
|T|
∇p(z
i
)
p(z
i
)
∂z
i
∂x
i
+ χ(x
i
), (5)
with
χ(x
i
) =
1
|T|
1
|T
y
i
|
∑
t
j
∈T
∇K
h
(x
j
− x
i
)
p(x
j
|y
i
)
. (6)
The term χ(·) in (6) is difficult to estimate. However
if the Parzen kernel K
h
(·) has a narrow window size,
only samples very close to the actual estimation point
will contribute to the pdf. Under this assumption the
conditional pdf is p(s|y
i
) ≈ N
s
/|T
y
i
|, where N
s
is the
number of pixels equal to s. Thus by substituting and
observing that ∇K
h
(·) is an odd function, we observe
that χ(x
i
) is negligible for almost every value assumed
by x
i
. In the following we will not consider this term.
Thus the energy derivative is a mean-shift (Comaniciu
and Meer, 2002) term on the high dimensional joint
pdf multiplied by a projection term. The mean-shift
is a simple estimate (Fukunaga and Hostetler, 1975)
of ∇log p(z
i
).
∇p(z
i
)
p(z
i
)
=
d + 2
h
2
1
k(z
i
,h)
∑
z
j
∈S
h
(z
i
)
K
h
(z
j
− z
i
), (7)
where d is the dimension of Z, S
h
(z
i
) is the support of
the Parzen kernel centered at point z
i
and of size h, k
being the number of observation falling into S
h
(X).
2.3 Limitations of Parzen Windowing
The Parzen method makes no assumption about the
actual PDF and is therefore qualified as nonparamet-
ric. The choice of the kernel window size h is criti-
cal (Scott, 1992). If h is too large, the estimate will
suffer from too little resolution, otherwise if h is too
small, the estimate will suffer from too much statisti-
cal variability.
As the dimension of the data space increases, the
space sampling gets sparser (problem known as the
curse of dimensionality). Therefore, less samples
fall into the Parzen window centered on each sample,
making the PDF estimation less reliable. Dilating the
Parzen window does not solve this problem since it
leads to over-smoothing the PDF. In a way, the limita-
tions of the Parzen Method come from the fixed win-
dow size: the method cannot adapt to the local sample
density. The k-th nearest neighbor (kNN) framework
provides an advantageous alternative.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
578

2.4 K-th Nearest Neighbor Method
In the Parzen-window approach, the PDF at sample
s is related to the number of samples falling into a
window of fixed size centered on the sample. The
kNN method is the dual approach: the density is
related to the size of the window necessary to in-
clude the k nearest neighbors of the sample. The
choice of k appears to be much less critical than the
choice of h in the Parzen method. In the kNN frame-
work, the mean-shift vector is given by (Fukunaga
and Hostetler, 1975)
∇p(z
i
)
p(z
i
)
=
d + 2
ρ
2
k




1
k
∑
z
j
∈S
ρ
k
z
j


− z
i


, (8)
where ρ
k
is the distance to the k-th nearest neighbor.
2.5 Adaptive Weighted kNN Approach
The kNN method provides several advantages with
respect to the Parzen Window method such as the
number of samples falling in the window is fixed and
known. Thus even if the space sampling gets sparser,
we cannot have windows with zero samples falling
into them. Moreover, the window size is locally adap-
tive. However, near the distribution modes there is a
high density of samples. The window size associated
to the k-th nearest neighbor could be too small. In
this case the estimate will be sensible to the statistical
variation in the distribution. To avoid this problem
we would increase the number of nearest neighbors,
to have an appropriate window size near the modes.
However this choice would produce in the tails of the
distribution a window too large. Thus very far sam-
ples would contribute to the estimation.
We propose, as an alternative solution, to weight the
contribution of the samples, i.e.,
1
k
∑
z
j
∈S
ρ
k
z
j
→
1
∑
k
j=1
w
j
k
∑
j=1
z
j
∈S
ρ
k
w
j
z
j
. (9)
Intuitively, the weights must be a function of distance
between the actual sample and the j-th nearest neigh-
bor, i.e., samples with smaller distance are weighted
more heavily than ones with larger distance. Several
weight functions (WFs) may be considered. For in-
stance, a simple function is
w
j
= 1 −

ρ
j
ρ
k

p
with p ∈ [0,+∞[, (10)
where ρ
j
is the distance to the actual sample of the jth
nearest neighbor and ρ
k
indicate the distance of the
farthest (k-th) neighbor. For p = 1, eq.(10) is equiv-
alent to the linear WF proposed by Dudani (Dudani,
1976) and for p = 2, we have a quadratic WF. Draw-
backs of this simple WF are the zero-value at bound-
aries and the function behavior fixed by the ρ
k
value.
Let us consider now a gaussian WF
w
j
= exp−
(ρ
j
/ρ
k
)
2
α
. (11)
In particular this WF is equivalent to apply a gaus-
sian mask of variance α/2 in the actual window of
size ρ
k
. As max
j
ρ
j
/ρ
k
= 1, the weights belong to
[exp−1/α,1]. Thus an appropriate value of α must
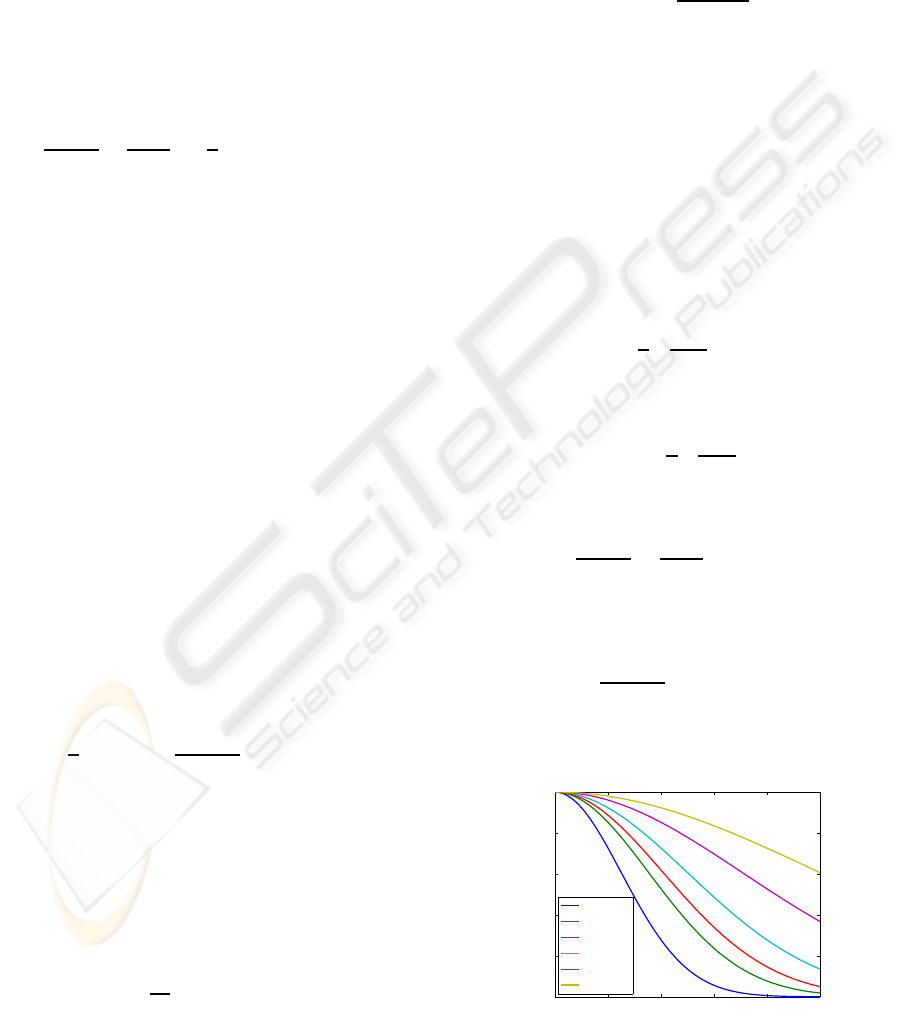
be chosen (see Fig.1). We would have a quite uniform
weighting process (large gaussian variance) when ρ
k
is not quite large (i.e., near the distribution modes),
and a smaller variance in the distribution tails (ρ
k
large) to reduce the effective window size. Thus a
single value for α is clearly inappropriate.
We propose an adaptive value for α to locally match
the distribution
α =
1
8

ρ
max
k
ρ
k

2
, (12)
and the corresponding WF is
w
j
= exp−
1
8

ρ
j
ρ
max
k

2
. (13)
Thus the mean shift term in (8) is replaced by
∇p(z
i
)
p(z
i
)
=
d + 2
ρ
2
k
M
k
(z
i
), (14)
where
M
k
(z
i
) =




1
∑
k
j=1
w
j
∑
j=1
z
j
∈S
ρ
k
w
j
z
j




− z
i
(15)
and w
j
given by eq.(13).
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
ρ
j
/ρ
k
w
j
α = 0.125
α = 0.250
α = 0.333
α = 0.500
α = 1.000
α = 2.000
Figure 1: Weight function behavior as function of α.
A MINIMUM ENTROPY IMAGE DENOISING ALGORITHM - Minimizing Conditional Entropy in a New Adaptive
Weighted K-th Nearest Neighbor Framework for Image Denoising
579

3 ALGORITHM OVERVIEW
The method proposed minimizes the conditional en-
tropy (3) using a gradient descent. The derivative
(5) is estimated in the adaptive weighted kNN frame-
work, as explained in section 2.5. In this case the term
∇p/p is expressed by eq.(14). Thus the steepest de-
scent algorithm is performed with the following evo-
lution equation
x
(n+1)
i
= x
(n)
i
− ν
d + 2
ρ
2
k
M
k
(z
i
)
∂z
i
∂x
i
, (16)
where ν is the step size.
At each iteration the mean-shift vector (15) in the high
dimensional space Z is calculated. The high dimen-
sional space is given by considering jointly the inten-
sity of the current pixel and that of its neighborhood,
as explained in section 2.1. The pixel value x
i
is then
updated by means of eq.(16).
The k nearest neighbors are provided by the Ap-
proximate Nearest Neighbor Searching (ANN) library
(Mount and Arya, ). Indeed computing exact nearest
neighbors in dimensions much higher than 8 seems to
be a very difficult task. Few methods seem to be sig-
nificantly better than a brute-force computation of all
distances. However, it has been shown that by com-
puting nearest neighbors approximately, it is possi-
ble to achieve significantly faster running times often
with a relatively small actual errors.
5 10 15 20 25
4
5
6
7
8
9
10
11
iteration
rmse
k = 10
k = 20
k = 30
k = 40
k = 50
k = 80
UINTA
0 5 10 15 20 25
0.5
0.6
0.7
0.8
0.9
1
iteration
SSIM index
k = 10
k = 20
k = 30
k = 40
k = 50
k = 80
UINTA
Figure 2: RMSE and SSIM in function of algorithm itera-
tions for different values of k.
a) b)
c) d)
Figure 3: Comparison of restored images. (a) Noisy image.
(b) UINTA restored. (c) kNN restored, k = 10. (d) kNN
restored, k = 40.
4 EXPERIMENTAL RESULTS
In this section, some results from the algorithm pro-
posed are shown. In order to measure the perfor-
mance of our algorithm we degraded the Lena im-
age (256x256 pixel) by adding a Gaussian noise with
standard deviation σ = 10. We consider a 9 x 9 neigh-
borhoods, and we add spatial features to the original
radiometric data (Elgammal et al., 2003; Boltz et al.,
2007). Formally, the PDF of Z(t), t ∈ T, is replaced
with the PDF of {Z(t),t},t ∈ T. These spatial fea-
tures allow us to reduce the effect of the non station-
arity of the signal in the estimation process, by pre-
ferring regions closer to the estimation point. The di-
mension of the data d is therefore equal to 83, and we
have to search the k nearest neighbors in such a high
dimensional space. Let us remind that the search is
performed using the ANN library. The algorithm per-
forms a gradient descent as described in section 3.
Figure3 shows a comparison of the restored images.
Fig.2 shows the RMSE and SSIM curves as a func-
tion of the algorithm iterations, for the UINTA (Awate
and Whitaker, 2006) algorithm, and our kNN based
restoration method with different values of k. In
Table1, the optimal values of the RMSE and SSIM
are shown. Our algorithm provides results compara-
ble with UINTA and slightly better when k ∈ [10;50].
However a small value of k produces some artifacts
in the restored images, as shown in Fig.4. A larger
value of k results in an increasing processing time.
Moreover the restored images seem to lost some de-
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
580

tails, for instance, on the hat. An intermediate value of
k = 40 is a good compromise between the quality of
the restored image and the processing time. In terms
of speed, our algorithm is much faster than UINTA,
due to the adaptive weighted kNN framework. In-
deed, UINTA have to update the Parzen window size
at each iteration. To do this a cross validation opti-
mization is performed. On the contrary our method
simply adapts the PDF changes during the minimiza-
tion process. For instance, cpu time in the Matlab
environment for standard UINTA algorithm is almost
4500 sec. Our algorithm, with k = 10, only requires
around 600 sec.
Table 1: RMSE and SSIM values for different values of k,
and for UINTA.
k RMSE SSIM
3 5.511 0.918
5 4.219 0.917
10 4.012 0.910
15 4.061 0.907
20 4.142 0.905
30 4.347 0.895
40 4.498 0.889
50 4.642 0.882
80 4.960 0.867
100 5.117 0.832
200 5.541 0.805
UINTA 4.651 0.890
5 CONCLUSIONS
This paper presents a restoration method in the vari-
ational framework based on the minimization of the
conditional entropy using the kNN framework. In par-
ticular a new adapted weighted kNN (AWkNN) ap-
proach has been proposed. The simulations indicated
slightly better results in RMSE and SSIM measures
w.r.t. the UINTA algorithm and a marked gain in cpu
speed. This gain is due to the property of AWkNN
that simply adapts the PDF changes during the min-
imization process. Results are even more promising
considering that no regularization is applied.
As future works, a regularization method will be
taken into account. Moreover, the feature space di-
mension can be boosted by taking into account other
image related features. For instance, the image gradi-
ent components can be used as additional features.
REFERENCES
Ahmad, I. A. and Lin, P. (1976). A nonparametric estima-
tion of the entropy for absolutely continuous distribu-
tions. IEEE Transactions On Information Theory.
Awate, S. P. and Whitaker, R. T. (2006). Unsupervised,
information-theoretic, adaptive image filtering for im-
age restoration. IEEE Trans. Pattern Anal. Mach. In-
tell., 28(3):364–376.
Boltz, S., Debreuve, E., and Barlaud, M. (2007). High-
dimensional statistical distance for region-of-interest
tracking: Application to combining a soft geomet-
ric constraint with radiometry. In IEEE International
Conference on Computer Vision and Pattern Recogni-
tion, Minneapolis, USA. CVPR’07.
Carlsson, G., Ishkhanov, T., de Silva, V., and Zomorodian,
A. (2007). On the local behavior of spaces of natural
images. International Journal of Computer Vision.
Comaniciu, D. and Meer, P. (May, 2002). Mean shift: A
robust approach toward feature space analysis. IEEE
Transactions On Pattern Analysis And Machine Intel-
ligence, 24, NO.5:603–619.
Cover, T. and Thomas, J. (1991). Elements of Information
Theory. Wiley-Interscience.
Dudani, S. (1976). The distance-weighted k-nearest-
neighbor rule. 6(4):325–327.
Elgammal, A., Duraiswami, R., and Davis, L. S. (2003).
Probabilistic tracking in joint feature-spatial spaces.
pages 781–788, Madison, WI.
Fukunaga, K. and Hostetler, L. D. (January, 1975). The es-
timation of the gradient of a density function, with ap-
plications in pattern recognition. IEEE Transactions
On Information Theory, 21, NO.1:32–40.
Geman, S. and Geman, D. (1990). Stochastic relaxation,
gibbs distributions, and the bayesian restoration of im-
ages. pages 452–472.
Huang, J. and Mumford, D. (1999). Statistics of natural
images and models. pages 541–547.
Lee, A. B., Pedersen, K. S., and Mumford, D. (2003). The
nonlinear statistics of high-contrast patches in natural
images. Int. J. Comput. Vision, 54(1-3):83–103.
Mount, D. M. and Arya, S. Ann: A library
for approximate nearest neighbor searching.
http://www.cs.umd.edu/ mount/ANN/.
Scott, D. (1992). Multivariate Density Estimation: Theory,
Practice, and Visualization. Wiley.
Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.
(APRIL, 2004). Image quality assessment: From error
visibility to structural similarity. IEEE Transactions
On Image Processing, 13, NO.4:600–612.
APPENDIX
In this section the calculus of the derivativeof the con-
ditional entropy of eq.(3) is performed. Let us remind
A MINIMUM ENTROPY IMAGE DENOISING ALGORITHM - Minimizing Conditional Entropy in a New Adaptive
Weighted K-th Nearest Neighbor Framework for Image Denoising
581

a) Degraded image b) k = 10 c) k = 20 d) k = 30
e) k = 40 f) k = 50 g) k = 80 h) k = 100
Figure 4: Comparison of knn restored images with different values of k.
that
h(X|Y = y
i
) ≈ −
1
|T|
∑
t
j
∈T
log p(x
j
|y
i
) (17)
and
p(s|y
i
) =
1
|T
y
i
|
∑
t
m
∈T
y
i
K(s− x
m
), (18)
where T
y
i
is the set of index pixels which have the
same neighborhood y
i
. Thus we have
h(X|Y = y
i
) = −
1
|T|
∑
t
j
∈T
log


1
|T
y
i
|
∑
t
m
∈T
y
i
K(x
j
− x
m
)


.
(19)
and, by taking the derivative of (19),
∂h(X|Y = y
i
)
∂x
i
= −
1
T
∑
t
j
∈T
1
p(x
j
|y
i
)
1
T
y
i
∑
t
m
∈T
y
i
∂K(x
j
− x
m
)
∂x
i
.
(20)
The last term in (20) is equal to
∂K(x
j
− x
m
)
∂x
i
=

−∇K(x
j
− x
m
)δ
m−i
j 6= i
(1− δ
m−i
)∇K(x
j
− x
m
) j = i
(21)
Thus by substituting
∂h(X|Y = y
i
)
∂x
i
= −
1
|T|
∇p(x
i
|y
i
)
p(x
i
|y
i
)
+
1
|T|
1
|T
y
i
|
∑
t
j
∈T
∇K(x
j
− x
i
)
p(x
j
|y
i
)
.
(22)
By multiplying the numerator and denominator of the
first term in (22) with p(y
i
)
∇p(x
i
|y
i
)
p(x
i
|y
i
)
·
p(y
i
)
p(y
i
)
=
∇p(z
i
)
p(z
i
)
·
∂z
i
∂x
i
, (23)
where the projection operator ∂z
i
/∂x
i
is because we
change from x
i
to z
i
. Finally, the derivative of (3) is
∂h(X|Y = y
i
)
∂x
i
= −
1
|T|
∇p(z
i
)
p(z
i
)
∂z
i
∂x
i
+
1
|T|
1
|T
y
i
|
∑
t
j
∈T
∇K(x
j
− x
i
)
p(x
j
|y
i
)
.
(24)
The second additional term can be neglected under
certain hypothesis. Thus the energy derivative is a
mean-shift (Comaniciu and Meer, 2002) term on the
high dimensional joint pdf multiplied by a projection
term.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
582