
GEOMETRIC ALGORITHMS ON CUDA
Antonio J. Rueda and Lidia Ortega
University of Ja´en. Escuela Polit´ecnica Superior. Paraje Las Lagunillas s/n, 23071, Ja´en, Spain
Keywords:
GPGPU, CUDA, 3D meshes, inclusion test, self-intersection test.
Abstract:
The recent launch of the NVIDIA CUDA technology has opened a new era in the young field of GPGPU
(General Purpose computation on GPUs). This technology allows the design and implementation of parallel
algorithms in a much simpler way than previous approaches based on shader programming. The present work
explores the possibilities of CUDA for solving basic geometric problems on 3D meshes like the point inclusion
test or the self-intersection detection. A solution to these problems can be implemented in CUDA with only a
small fraction of the effort required to design and implement an equivalent solution using shader programming,
and the results are impressive when compared to a CPU execution.
1 INTRODUCTION
The General Purpose computation on GPUs
(GPGPU) is a young area of research that has
attracted attention of many research groups in the last
years. Although graphics hardware has been used
for general-purpose computation since the 1970s,
the flexibility and power processing of the modern
graphics processing units (GPUs) has generalized its
use for solving many problems in Signal Processing,
Computer Vision, Computational Geometry or
Scientific Computing (Owens et al., 2007).
The programming capabilities of the GPU evolve
very rapidly. The first models only allowed lim-
ited vertex programing; then pixel programing was
added and gradually, the length of the programs and
its flexibility (use of loops, conditionals, texture ac-
cesses, etc.) were increased. The last generation of
NVIDIA GPUs (8 Series) supports programming at a
new stage of the graphics pipeline: the geometry as-
sembling. GPU programming has been extensively
used in the last years for implementing impressive
real-time physical effects, new lighting models and
complex animations (Fernando, 2004; Pharr and Fer-
nando, 2005), and have allowed a major leap forward
in the visual quality and realism of the videogames.
But it should be kept in mind that vertex, pixel
and geometry programming capabilities were aimed
at implementing graphics computations. Their use
for general purpose computing is difficult in many
cases, implying the complete redesign of algorithms
whose implementation in CPU require only a few
lines. Clearly the rigid memory model is the biggest
problem: memory reads are only possible from tex-
tures or a limited set of global and varying parame-
ters, while memory writes are usually performed on a
fixed position in the framebuffer. Techniques such as
multipass rendering, rendering to texture, and use of
textures as lookup tables are useful to overcome these
limitations, but programming GPUs remains being a
slow and error-prone task. On the positive side, the
implementation effort is usually compensated with a
superb performance, up to 100X faster than CPU im-
plementations in some cases.
The next step in the evolution of GPGPU is the
CUDA technology of NVIDIA. For the first time, a
GPU can be used without any knowledge of OpenGL,
DirectX or the graphics pipeline, as a general pur-
pose coprocessor that helps the CPU in the more com-
plex and time-expensivecomputations. With CUDA a
GPU can be programmed in C, in a very similar style
to a CPU implementation, and the memory model is
now simpler and more flexible.
In this work we explore the possibilities of the
107
J. Rueda A. and Ortega L. (2008).
GEOMETRIC ALGORITHMS ON CUDA.
In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 107-112
DOI: 10.5220/0001094201070112
Copyright
c
SciTePress

CUDA technology for performing geometric compu-
tations, through two case-studies: point-in-mesh in-
clusion test and self-intersection detection. So far
CUDA has been used in a few applications (Nguyen,
2007) but this is the first work which specifically com-
pares the performance of CPU vs CUDA in geometric
applications.
Our goal has been to study the cost of implemen-
tation of two typical geometric algorithms in CUDA
and its benefits in terms of performance against equiv-
alents CPU implementations. The algorithms used
in each problem are far from being the best, but the
promising results in this initial study motivate a future
development of optimized CUDA implementations of
these and similar geometric algorithms.
2 COMMON UNIFIED DEVICE
ARCHITECTURE (CUDA)
The CUDA technology was presented by NVIDIA
in 2006 and is supported by its latest generation of
GPUs: the 8 series. A CUDA program can be imple-
mented in C, but a preprocessor called NVCC is re-
quired to translate its special features into code that
can be processed by a C compiler. Therefore host
and device CUDA code can now be combined in a
straightforward way.
A CUDA-enabled GPU is composed of several
MIMD multiprocessors that contain a set of SIMD
processors (NVIDIA, 2007). Each multiprocessor has
a shared memory that can be accessed from each of its
processors, and there is a large global memory com-
mon to all the multiprocessors. Shared memory is
very fast and is usually used for caching data from
global memory. Both shared and global memory can
be accessed from any thread for reading and writing
operations without restrictions.
A CUDA execution is composed of several blocks
of threads. Each thread performs a single computa-
tion and is executed by a SIMD processor. A block is
a set of threads that are executed on the same multi-
processor and its size should be chosen to maximize
the use of the multiprocessor. A thread can store data
on its local registers, share data with others threads
from the same block through the shared memory or
access the device global memory. The number of
blocks usually depends on the amount of data to pro-
cess. Each thread is assigned a local identifier inside
the block with three components, starting at (0, 0,
0), although in most cases only one component (x) is
used. The blocks are indexed using a similar scheme.
A CUDA computation starts at a host function by
allocating one or more buffers in the device global
memory and transferring the data to process to them.
Another buffer is usually necessary to store the results
of the computation. Then the CUDA computation
is launched by specifying the number of blocks and
threads per block, and the name of the thread function.
The thread function retrieves the data to process from
the data buffers, which are passed as pointers. Then
the computation is performed and the result stored in
the results buffer. Finally, the host function retrieves
the results buffer to CPU memory.
The learning curve of CUDA is much faster
than that of GPGPU based on shader program-
ming with OpenGL/DirectX and Cg/HLSL/GLSL.
The programming model is more similar to CPU pro-
gramming, and the use of the C language makes
most programmers feel comfortable. CUDA is also
designed as an stable scalable API for developing
GPGPU applications that will run on several gener-
ations of GPUs. On the negative side, CUDA loses
the powerful and efficient mathematical matrix and
vector operators that are available in the shader lan-
guages, in order to keep its compatibility with the C
standard. It is likely that in many cases an algorithm
carefully implemented in a shader language could run
faster than its equivalent CUDA implementation.
3 POINT-IN-MESH INCLUSION
TEST ON CUDA
The point-in-mesh inclusion test is a simple classical
geometric algorithm, useful in the implementation of
collision detection algorithms or in the conversion to
voxel-based representations. A GPU implementation
of this algorithm is only of interest with large meshes
and many points to test, as the cost of setting up the
computation is high.
For our purpose we have chosen the algorithm
of Feito & Torres (Feito and Torres, 1997) which
presents several advantages: it has a simple imple-
mentation, it is robust and can be easily parallelized.
The pseudocode is shown next:
bool inclusionTest(Mesh M, Point p)
o = point(0, 0, 0) // Origin point
res = 0 // Inclusion counter
foreach face f of M do
t = tetrahedron(f, o)
if inside(t, p) then
res = res + 1
elseif atFaces(t, p) then
res = res + 0.5
endif
endforeach
return isOdd(res)
end
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
108
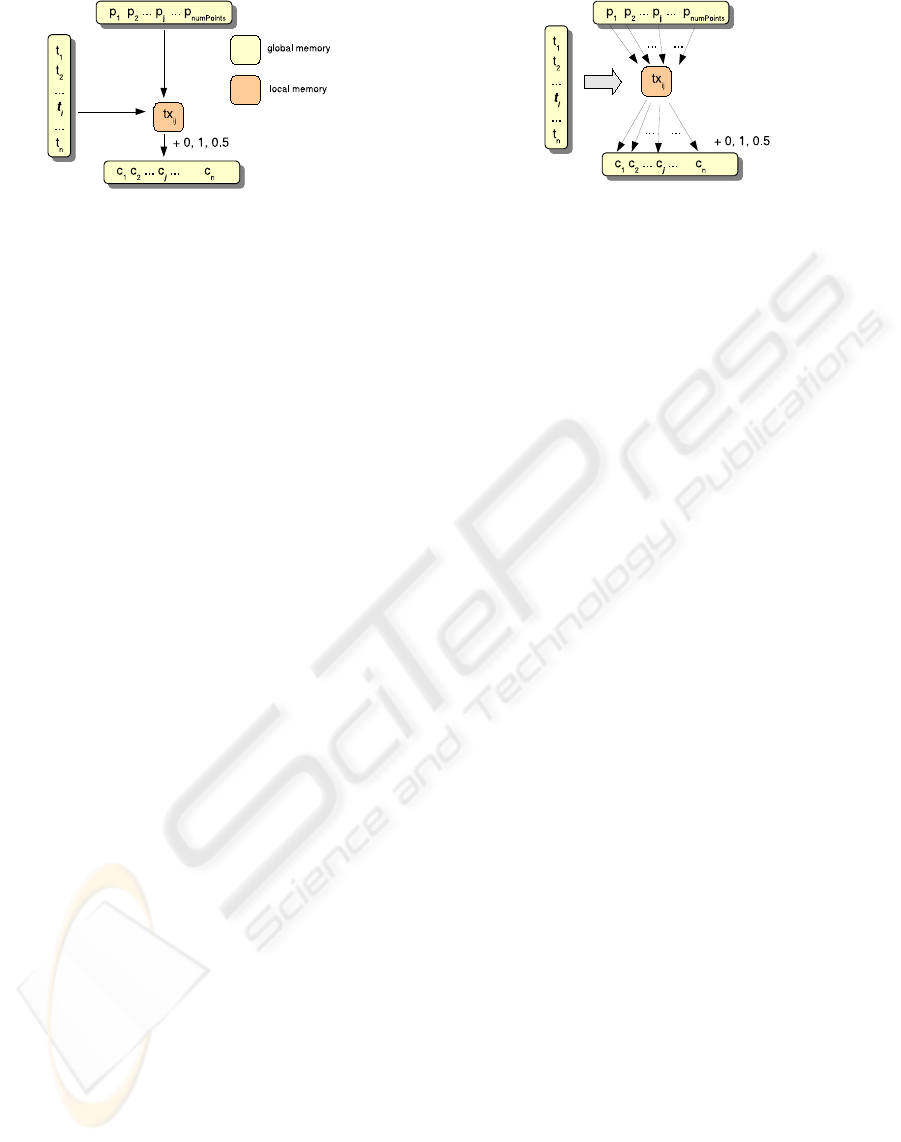
Figure 1: CUDA matrix-based implementation of the inclu-
sion test.
The algorithm constructs a set of tetrahedra between
the origin of coordinates and each triangular face of
the mesh. The point is tested for inclusion against
each tetrahedron and a counter is incremented if the
result of the test is positive. If the point is inside an
odd number of tetrahedra, the point is inside the mesh.
Notice that if the point is at a face shared by two tetra-
hedra, the counter is added 0.5 by each one to avoid a
double increment that would lead to incorrect results.
The programming model of CUDA fits especially
well with problems whose solution can be expressed
in a matrix form. In our case, we could construct a
matrix in which the rows are the tetrahedra to pro-
cess and the columns, the points to test. This matrix
is divided into blocks of threads, and each thread is
made responsible of testing the point in the column
j against the tetrahedron in the row i, and adding the
result of the test (0,1,0.5) to the counter j (see Fig-
ure 1). Unfortunately, this approach has an important
drawback: the support for atomic accesses to mem-
ory, that ensure a correct result after read-write opera-
tions on the same value in global memory performed
from several concurrent threads, is only available in
devices of compute capability 1.1, that is the GeForce
8500 and 8600 series (NVIDIA, 2007). This prob-
lem can be avoided if each thread stores the result of
the point-in-tetrahedron inclusion test in the position
(i, j) of a matrix of integers. After the computation,
the matrix is retrieved to CPU memory, and each in-
clusion counter j is simply calculated from the sum
of the values of the row j. But this implementation
makes an inefficient use of the device memory, requir-
ing the allocation of a huge matrix when working with
large meshes and many points to test. Moreover these
two approaches generates an overwhelming number
of threads during the GPU execution, which leads to
poor results.
We choose a different strategy, computing in each
thread the inclusion test of one or severalpoints on the
entire mesh. Each thread iterates on the mesh, copy-
ing a triangle from global memory to a local variable
and performing the inclusion test on the points, then it
accumulates the result in a vector that stores an inclu-
Figure 2: CUDA implementation of the inclusion test.
sion counter per point (Figure 2). It could be argued
that the task assigned to each thread is very heavy,
specially when compared with the matrix-based im-
plementations but in practice it works very well. Two
implementation aspects require a special attention.
First, the accesses from the threads to the triangle list
must be interleaved to avoid conflicts that could pe-
nalize performance. And second, the relatively high
cost of retrieving a triangle from global memory to a
processor register makes interesting testing it against
several points. These points must be also cached in
processor registers for maximum performance, and
therefore its number is limited.
The host part of the CUDA computation starts
by allocating a buffer of triangles and a buffer of
points to test in the device memory, and copying
these from the data structures in host memory. An-
other buffer is allocated to store the inclusion coun-
ters, which are initialized to 0. The number of blocks
of threads are estimated as a function of the total
number of points to test, the number of points per
block and the number of points processed by a sin-
gle thread: numBlocks = numPoints/(BLOCKSIZE∗
THREADPOINTS). The last two constants should
be chosen with care to maximize performance: a high
number of threads per block limits the number of reg-
isters available in a thread, and therefore, the num-
ber of points that can be cached and processed. A
low number of threads per block makes a poor use of
the multiprocessors. Finally, after the GPU computa-
tion has completed, the buffer of inclusion counters is
copied back to the host memory.
A thread begins by copying THREADPOINTS
points from the point buffer in global memory to a
local array, that is stored in registers by the CUDA
compiler. The copy starts at the position (blockIdx.x∗
BLOCKSIZE + threadIdx.x) ∗ THREADPOINTS to
assign a different set of points to each thread. Af-
ter this, the iteration on the triangle list starts by
copying the triangles to a local variable and call-
ing a point-in-tetrahedron inclusion test function. In
case of success, the inclusion counter of the corre-
sponding point is updated. A good interleaving is en-
GEOMETRIC ALGORITHMS ON CUDA
109

Figure 3: Models used for running the inclusion and self-
intersection tests.
sured by starting the iteration at the position given by
blockIdx.x∗ BLOCKSIZE + threadIdx.x.
We implemented a CUDA version of the algo-
rithm, using blocks of 64 threads and testing 16 points
per thread, and an optimized version for CPU. The
computer used for the experiments has an Intel Core
Duo CPU running at 2.33Ghz., a NVIDIA GeForce
8800GTX GPU and Linux-based operating system.
Four different models, with increasing number of
faces were used (Figure 3). The improvements of
the GPU against the CPU version of the algorithm are
shown in Table 1. As expected, the CPU only beats
the GPU implementation with very simple meshes. In
the rest of cases, the GPU outperforms the CPU up
to 77X in the case of the largest model and higher
number of points to test. Notice that the GPU com-
pletes this computation in less than 7 seconds, while
the CPU requires 8 minutes.
4 SELF-INTERSECTION TEST
ON CUDA
Triangle-mesh is nowadays the most extended method
of representing 3D models. The higher number of tri-
angles representing the surface, the higher is the re-
alism sensation when rendering the figure. Further-
more, meshes need to be well-formed in order to pro-
vide accuracy to different geometric algorithms. In
this context, incomplete connection meshes (meshes
with unnecessary holes) or self-intersection faces,
make some algorithms work wrong. For instance, a
3-Dimensional printer needs a hole-free mesh to be
able to produce the physical model, and the inclusion
test described in Section 3 needs non-selfintersection
meshes to reach to successful results.
We find different CPU strategies in the literature
to detect, prevent or eliminate self-intersections in tri-
angle meshes (Gain and Dogsson, 2001; Lai and Laia,
2006). However in many cases the difficulty of these
improved approaches is not worthwhile with the ob-
tained time-improvement of the straightforward solu-
tion.
The same argument can be used for GPGPU al-
gorithms based on shader programming, such as the
method proposed in (Choi et al., 2006) for detecting
self-intersections in triangle meshes. One of the most
interesting applications to self-collisions detection is
the interactive simulation of deformable objects in
real-time. Some examples are deformations of hu-
man organs and soft tissue, clothed articulated human
characters, elastic materials, etc. In all these cases the
computational bottleneck is collision detection. The
major time improvement found for this approach is
17X, after applying a GPU algorithm with different
steps including: a previous phase to discard triangles
using visibility-based culling; a second step imple-
ments the topological culling using an stencil test with
the aim of discarding pairs of triangles as well; and
finally the remaining set of triangle pairs are exam-
ined for collisions using M¨oller triangle-triangle test
(Moller, 1997). The process uses three 1D textures
to represent the triangles, a quadrilateral for all pair-
wise combination and a hierarchical readback struc-
ture in order to improve the readback of collision re-
sults from GPU.
We propose a CUDA based solution for self-
intersection detection, joining simplicity in the imple-
mentation and gaining overall performance, as shown
in the implementation results. The straightforward
CPU algorithm compares each triangle with the rest
of faces in the mesh, searching for intersections. The
result is an array of booleans for each face in the
mesh:
void selfintersecTest(Mesh M,bool res[])
foreach face
f
i
of M do
res[i] = false // default result
foreach face
f
j
of M do
if (i!= j)
if (IntersecTriTri(
f
i
,
f
j
)) then
res[i] = true
break
endif
endif
endforeach
endforeach
end
We use this simple approach with the additional ad-
vantage of the straightforward parallelization using
different criteria. Several of them have been tested
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
110
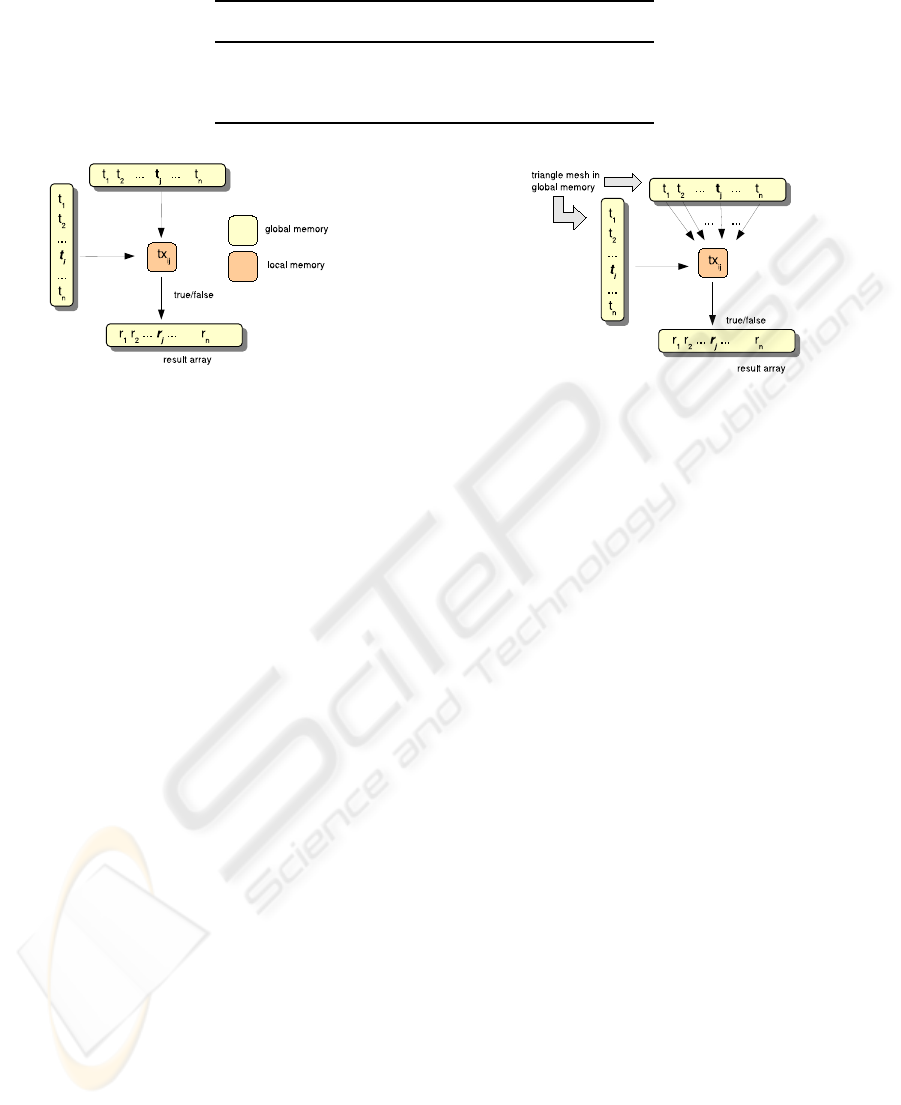
Table 1: Improvements of the GPU vs the CPU implementation of the inclusion test algorithm.
number of points tested
mesh (number of triangles) 1000 10000 100000
simple (42) 0.05 0.5 3.7
heart (1619) 1.2 10 38
bone (10044) 2.6 29 55
brain (36758) 3.5 35 77
Figure 4: CUDA matrix-based implementation of the self-
intersection test.
carrying out interesting conclusions. We next de-
scribe two of these strategies.
The first approach we have tested uses a matrix
form, following the scheme of Figure 4, in a similar
way to the first approach of the inclusion test. Each
face f
i
(row) is tested for intersection against face f
j
(column) in a thread using M¨oller triangle-triangle in-
tersection test (Moller, 1997). If face f
i
finds at least
one intersection, a true value is written in i position of
the result array, res[i] = true. Each block works with
BLOCKSIZExBLOCKSIZE threads. The number of
blocks is consequently (nTriangles/BLOCKSIZE x
nTriangles/BLOCKSIZE).
Our experiments have been carried out in the same
computer configuration described for the inclusion
test in Section 3, with 64 threads per block, this is,
BLOCKSIZE=8. A greater value does not guarantee a
successful execution in CUDA. We have found faster
GPU running times for this approach in the range
3X − 16X for meshes from 1, 619 to 36,758 triangles.
However, this scheme of solution is not the op-
timal one. Surprisingly, a more efficient approach
comes by a simpler strategy (observe Figure 5): each
thread is charged of testing one face against the rest
of nTriangles − 1 triangles in the mesh. The num-
ber of threads per block is BLOCKSIZE and the
number of blocks is nTriangles/BLOCKSIZE. As
each thread deals with only one face of the trian-
gle list and writes the solution in only one position
in the result array, there is no synchronization prob-
lems acceding to global memory. The exclusive tri-
angle that each thread processes is retrieved from
global to local memory from the position blockIdx.x∗
Figure 5: CUDA implementation of the self-intersection
test.
BLOCKSIZE + threadIdx.x, with the additional ad-
vantage of providing good interleaving. Even though
the charge of work associated to each thread is really
significant, the cost of retrieving triangles from global
to local memory is minimized.
We show in Table 2 the results obtained for dif-
ferent meshes considering BLOCKSIZE = 64. The
best results are found in larger meshes, for instance,
the brain needs 3,6 minutes in CPU and less than 6
seconds in GPU to detect its self-intersections.
5 CONCLUSIONS AND FUTURE
WORKS
After running different geometric algorithms for 3D
meshes with different approaches, we reach some
conclusions about using CUDA technology:
• Most of the geometric algorithms can be rewritten
for CUDA, however the best running times are ob-
tained in quadratic algorithms whose paralleliza-
tion strategy can be given in a matrix form. Linear
algorithms as the computation of a bounding box,
are much more efficient in CPU. The same con-
clusion can be drawn for some hierarchical par-
allel algorithms, such as the construction of the
convex hull. In this case many threads can work
independently discarding points in partial convex
hulls, however at the end of the iterative process,
only one thread must merge all partial solutions,
what slows down the process. Furthermore, in the
GEOMETRIC ALGORITHMS ON CUDA
111

Table 2: Improvements of the GPU vs the CPU implementation of the self-intersection test algorithm.
mesh (number of triangles) improvements CPU time(ms) GPU time(ms)
simple (42) 0.06 0.57 104
heart (1619) 4.22 462 109
bone (10044) 42 24524 583
brain (36758) 39 217700 5596
worst case all vertices are in the convex hull (sup-
pose a 3D ball), what suppose a total lack of par-
alellization.
• The algorithms we studied in this paper, the in-
clusion and the self-intersection tests, are both
quadratic algorithms. However the best CUDA
implementation in both cases rules out a matrix
parallelization, overloading each thread with a lin-
ear process that reduces the retrieving from global
memory to the processor registers. Therefore,
in the inclusion test, a thread deals with several
points that are tested for inclusion on the entire
mesh. The self-intersection approach also special-
izes each thread in a simple face in order to run the
triangle-triangle intersection test against the rest
of triangles of the mesh. The best comparative re-
sults are obtained for meshes with a high number
of triangles.
• A further characteristic of the algorithms tested in
this paper are that threads do not need synchro-
nization to access to memory positions and neither
they have to share data to provide a joint solution.
All threads can work independently, what speeds
up the execution. However not all problems can
be solved by this simple solution, needing syn-
chronization when acceding to shared or global
memory using sentences as syncthreads().
As a final conclusion, CUDA technology for GPGPU-
based algorithms can be considered a gamble on the
next future because of the small effort required in the
CPU-GPU translation and implementation of the al-
gorithms, as well as the performance improvement
against the same version of the CPU approach. In
many cases, this technology obtains better results us-
ing straightforward versions of the solutions com-
pared with optimized approaches in CPU that usually
use sophisticated data structures.
We expect that successive generations of NVIDIA
GPUs will be able to support new features, as the
atomic access to memory in recent GeForce 8500
and 8600 series. Our next goal consists of applying
CUDA to different Computer Graphics and Computa-
tional Geometry problems such as collision detection,
mesh simplification, or compresion and LOD tech-
niques.
ACKNOWLEDGEMENTS
This work has been partially granted by the Minis-
terio de Ciencia y Tecnolog´ıa of Spain and the Eu-
ropean Union by means of the ERDF funds, un-
der the research project TIN2004-06326-C03-03 and
TIN2007-67474-C03-03 and by the Conserjer´ıa de
Innovaci´on, Ciencia y Empresa of the Junta de An-
daluc´ıa, under the research project P06-TIC-01403.
REFERENCES
Choi, Y.-J., Kim, Y. J., and Kim, M.-H. (2006). Rapid pair-
wise intersection tests using programmable gpus. The
Visual Computer, 22(2):80–89.
Feito, F. and Torres, J. (1997). Inclusion test for general
polyhedra. Computer & Graphics, 21:23–30.
Fernando, R. (2004). GPU Gems: Programming Tech-
niques, Tips and Tricks for Real-Time Graphics. Pear-
son Higher Education.
Gain, J. E. and Dogsson, N. A. (2001). Preventing self-
intersection under free-form deformation. IEEE Tran-
sations On Visualization and Computer Graphics, 7.
Lai, J.-Y. and Laia, H.-C. (2006). Repairing triangular
meshes for reverse engineering applications. Ad-
vances in Engineering Software, 37(10):667–683.
Moller, T. (1997). A fast triangle-triangle intersection test.
journal of graphics tools, 2(2):25–30.
Nguyen, H. (2007). GPU Gems 3. Addison-Wesley Profes-
sional.
NVIDIA, C. (2007). NVIDIA CUDA Programming Guide
(version 1.0). NVIDIA Corporation.
Owens, J. D., Luebke, D., Govindaraju, N., Harris, M.,
Krger, J., Lefohn, A. E., and Purcell, T. J. (2007).
A survey of general-purpose computation on graphics
hardware. Computer Graphics Forum, 26(1):80–113.
Pharr, M. and Fernando, R. (2005). GPU Gems 2 : Pro-
gramming Techniques for High-Performance Graph-
ics and General-Purpose Computation. Addison-
Wesley Professional.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
112
