IMAGE-BASED 3D TORSO BODY MODELING

3D Female Body Modeling for Breast Surgery Simulation

Youngjun Kim, Kunwoo Lee

Human-Centered CAD Lab., Seoul National University, ShilimDong, KwanakGu, Seoul, Korea

Wontae Kim

K&I Technology, 1586-6, SeochoDong, SeochoGu, Seoul, Korea

Keywords: Human body, image-based 3D modeling, breast surgery.

Abstract: This paper proposes an image-based 3D modeling algorithm for a 3D torso of the human body. This

approach provides an easy and practical way of modeling so that doctors can obtain the subject’s 3D data

without additional equipment such as a 3D scanner or MRI. To achieve this goal, a 3D template model with

feature points is prepared, and then a 3D model of the subject is reconstructed from orthogonal photographs

by deforming the 3D template model. An appropriate number of feature points and their positions are

derived. Procrustes Analysis and Radial Basis Functions (RBFs) are applied for the deformation. After the

deformations, images are mapped onto the mesh for realistic visualization.

1 INTRODUCTION

Three dimensional human body modeling is one of

the most popular topics in the computer animation

and reverse-engineering fields. There are various

ways to get 3D human data, such as 3D scanning,

direct modeling, example-based modeling, etc.

Among them, image-based 3D human modeling is

one of the most attractive methods due to its

simplicity and practicality. However, although many

approaches have been applied to the face, few trials

have been done especially for the breast or torso

area. Image-based upper body modeling is more

difficult than face or head modeling because the

upper body has fewer dominant feature points.

The goal of this project is to develop virtual

simulation software for breast plastic surgery. For

breast surgeries, including breast augmentation and

other cosmetic purposes, virtual simulation may play

an important role in discussions between doctors and

patients. It also helps surgeons decide the best way

to operate. Many 2D simulation programs have

already been developed, but they lack realism, and

most are unnatural. For 3D breast simulation,

Balaniuk et al. implemented a 3D breast surgery

simulation using REM (Balaniuk, et al., 2006). They

are getting good results, but they use a 3D scanner to

get the subject’s body data and they simulate only

the breast. Our approach overcomes those

weaknesses. In this paper we propose a simple way

to reconstruct a female torso from photos. This is the

first stage of the virtual simulation for breast

surgery. We need only several photos of the subject,

and we can get a realistic 3D model of the upper

body. Based on the ideas of image-based head

modeling, we present efficient algorithms to

generate a 3D torso model from several images of a

subject. For this purpose, a template model with

feature points and segments is prepared. We deform

the template model to get the subject’s 3D data,

using orthogonal images of that person.

The remainder of the paper is organized as

follows. Section 2 describes the template model to

be deformed, and Section 3 explains the algorithms

of deformation to get the subject’s 3D model. The

results of our work are described in Section 4, and

future work is discussed in Section 5.

Kim Y., Lee K. and Kim W. (2008).

IMAGE-BASED 3D TORSO BODY MODELING - 3D Female Body Modeling for Breast Surgery Simulation.

In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 92-98

DOI: 10.5220/0001094500920098

 SciTePress

2 TEMPLATE MODEL

PREPARATION

2.1 3D Template Model

A generic model, or template model, is commonly

used for image-based body modeling. We call the

3D model a template model in this paper to avoid

confusion. The template model must have a typical

and representative shape. The mesh data should be

neat and clean. Because no template model data can

represent all body types, several types of template

models should be prepared. However, acquiring and

standardizing many scanned data of naked bodies

are not easy. For these reasons, we made template

models using modelling tools, rather than by

scanning an actual human body. We used MAYA

7.0 to make the 3D template model. Figure 1 shows

the template data.

Figure 1: A refined 3D template model: mesh display

mode (left) and wire-frame display mode (right).

2.2 Feature Point Definition

Feature points are necessary and important

prerequisites to get a realistic result in image-based

modeling. We referred to Lee’s definition (H. Lee, K.

Hong and E. Kim, 2004), and excluded some points

and defined some additional points for our purpose.

The number of feature points is 10 for the left and

right breasts, respectively. The two side-view

images are scaled according to the height of the

breast, from P0 to P4, in the front-view image. For

the abdominal part, 18 feature points (six points each

for the left, right and central waist curves,

respectively) are defined. These points are

automatically positioned by skin detection as

described in Section 3.2. Additional points such as

navel, armpit, shoulder, etc. are also defined. Table 1

and Figure 2 show the definitions of the feature

points.

Table 1: The definition of the feature points.

Pt Definition

Upper breast point (UBP),

same y-coord. as LAP on &

P1 Mid-point of P0 & P2 on

P2 Bust point (BP) on &

P3 Mid-point of P2 & P4 on

P4 Bottom breast point (BBP) on &

P5 Mid-point of P0 & P6 on

P6 Outermost point on

P7 Mid-point of P6 & P4 on

P8 Mid-point of P4 & P9 on

P9 Inner breast point (IBP),

FNP Front neck point

SP Shoulder point, same y-coord. as FNP

CSP

Center of shoulder point on ,

mid-point of FNP & SP in x-dir.

OBP

Outer breast point on ,

mid-point of P0 & P4 in y-dir.

WP1 Same y-coord. as P4, on or

WP2

~WP5

Equally dividing points between WP1 and WP6

in y-dir. on or

WP6 Same y-coord. as P4, on or

FCP

Front center point,

Mid-point of LBP9 & RBP9

Navel point,

the same point as WP6 on

: front -view image, : side-view image

: breast curve in

: waist curve in

: belly curve in

Figure 2: Definitions of the feature points (R: right, L: left,

C: centre).

3 TEMPLATE MODEL

DEFORMATION

3.1 Image Capture

In our image-based 3D torso body modeling, we use

a front-view and two side-view photographs of the

subject. We need both the left-view and right-view

images in order to reconstruct breasts that are not

symmetrical. A back-view photograph is optionally

added if needed for texture mapping. We define the

IMAGE-BASED 3D TORSO BODY MODELING - 3D Female Body Modeling for Breast Surgery Simulation

feature points from these orthogonal images. The

image for the texture mapping is also obtained from

them. Many postures of the subject were tested

considering the texture mapping and repeatability. A

white or blue background is recommended because

we detect the body curves by skin detection.

An image-capturing device is designed to get the

photos conveniently even though our software

allows any kind of digital images of subjects. Our

image-capturing device, which is connected to a PC

with a USB cable, consists of a digital camera and a

distance-checking sensor. The image captured by the

digital camera is sent directly to our software.

Olympus SDK v3.3 is applied to implement remote-

capturing (http://www.olympus.com/). An ultrasonic

sensor checks the distance from the object and gives

the distance information to our software. We can

roughly calculate the actual size of the subject using

calibration information according to the distance.

The images of several discrete positions of a

calibration panel are taken beforehand. Our system’s

distance range is 1-2m. Tsai’s calibration method is

applied to derive the relations between the image

coordinates and the world coordinates at each

position. Figure 3 shows our image-capturing device

and the calibration panel.

Figure 3: Photos of the image-capturing device (left) and

the calibration panel (right).

3.2 3D Feature Points’ Calculation

from Images

After taking pictures or loading the images of the

subject, we assign the feature points. All of the

points or each point can be scaled and translated

easily with our GUI. Some points are constrained by

the definition in Table 1, and many of them are

automatically positioned. For example, RSP and

LSP have the same y-coordinates as FNP. Their

coordinates in the front-view image are set at the

outmost positions of the body at the FNP’s y-level.

In Section 2.2, the feature points P0, P2 and P4

in the front-view image are assumed to lie on the

same plane in the 3D coordinate system. These

points are also defined in the side-view. Therefore,

x- and y-coordinates are assigned in the front-view

image and z- and y-coordinates are decided in the

left-view image. Internally, the side-view images are

scaled and normalized according to the front-view.

With these relationships, the coordinates of all the

feature points are derived. Their x-coordinates are

obtained from the front image, and the z-coordinates

are computed from the side image. The y-

coordinates are common values in the front and side

images. The amount of proper deformation of the

template model is obtained by the process of

matching the corresponding feature points in the

template to those in the images. Sections 3.3 and 3.4

describe the algorithms in detail.

WP1~WP6 are detected automatically using skin

detection. We used YCbCr colour space. We need to

handle only Cb and Cr values because we are

interested in the illumination intensity invariant part

of the colour for the skin detection. Eq. (1) below

shows our skin detection criteria:

(1)

where

= 77, = 132

= 133, = 171

In the skin detection process, we have many

small holes in the interior of the body. These holes

are obstacles to finding the body’s curves, so we fill

the holes if they are smaller than a threshold size

proportional to the image size. Figure 4 shows the

skin detection result and the feature points.

Figure 4: Skin detection result and feature points on 2D

front-view (left) and left-view (right) images. Some of the

points are positioned manually and the others are set

automatically.

3.3 Global Deformation

In the global deformation step, we compute the

affine transformation matrix to match the template

model as closely as possible to the feature points

calculated from the images. The affine

transformation includes translation, rotation and

scaling. To minimize the sum of the squared error

between the calculated feature points and the

corresponding feature points of the transformed

model, we use Procrustes Analysis (J.C. Gower and

G.B. Dijksterhuis, 2004). This method is

computationally simple and stable. This global

deformation is an auxiliary step because it gives

min

max

min

max

}&|),({

maxminmaxmin

CrCrCrCbCbCbyxp <<<

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

good initial conditions for local deformation.

Normalization of the data is also done in this step.

(2)

where

: Feature points calculated from images

: Feature points of template model

: scale factor

: rotation matrix

: translation vector

The procedures of the global deformation are as

follows:

a) Compute the mean of both and .

b) Center each set at its origin.

(i.e., )

c) Compute the norm of each set and .

d) Normalize each set to equal the unit norm.

(i.e.,

e) Let .

f) Compute the Singular Value Decomposition

(SVD) of

that results in the matrices L, D

and M.

(i.e.,

)(ASVDLDM =

)

g) Compute the rotation matrix

LR =

h) Compute the scaling factor.

i) Compute the translating vector.

j) Transform to using .

k) Finally, transform the entire 3D template

model’s vertices using

and

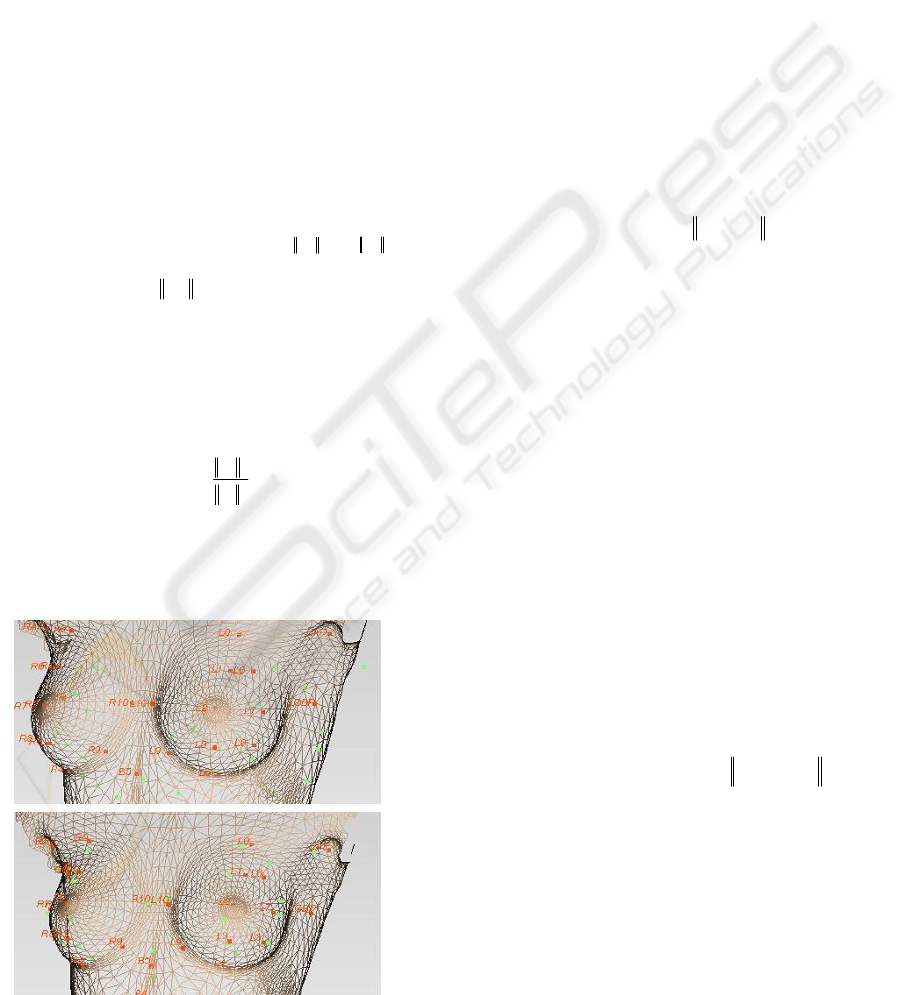
Figure 5: Before and after global deformation; red points

are and green points are .

3.4 Local Deformation

After global rigid deformation aligns the template

model to , local deformation refines and generates

a more realistic model. For this process, an

interpolation function is estimated, and the rest of

the points are mapped using this function. Among

the interpolation methods, Radial Basis Function

(RBF) is a powerful technique for interpolating in a

multidimensional space (Ruprecht and Müller, 1993.,

Carr, et al., 2001., Park, el al., 2005., etc). The basis

function,

R(d)

, depends only on the distance from

the feature points, which are thus called radials. RBF

constructs the interpolant as a linear combination of

basis functions and then determines the coefficients

of the basis functions. The concept of RBF is that

each vertex is influenced by all the feature points,

but the near feature points are more influential on

that vertex.

))(()()(

∑

−=

ippRiwpf

(3)

where

)(Pf

: transformed vertex through local deform

w(i)

: coefficients of the basis functions

p(i)

: model’s feature points

: each vertex of generic model (input point)

The most common radial basis functions,

R(d)

are as follows:

d R(d)

(linear)

d R(d) =

(cubic)

dlog(d) R(d)

(thin plate spline)

u/222

)c(d R(d) +=

(multiquadric)

-d/c

e R(d) =

(Gaussian)

We tested those radial basis functions and

selected the most appropriate one for our model:

(4)

To find the coefficients of the basis

functions,

w(i)

, we have Eq. (4) letting

)(

and

be equal.

(5)

where

: the x-coordinate of the j

calculated feature point

: the x-coordinate of the j

template model feature point

after global deformation

Because we have pairs of and , we can

solve Eq. (5) and get the basis functions’

coefficients.

∑

−=

)(),,(min

PPTRSE

⎥

⎦

⎤

⎢

⎣

⎡

⋅=

⎥

⎦

⎤

⎢

⎣

⎡

∑

×=

)(

DdiagonalS

00 CCC

PPP =

))(()()(

RPmeanSPmeanT

−=

00 T

PPA =

))(()()(

∑

−==

xTx

ippRiwpfp

N 1,2j

…

50/

)(

edR

−

)(

0 CCC

PmeanPP −=

TRPSP

⋅

⋅=

′

IMAGE-BASED 3D TORSO BODY MODELING - 3D Female Body Modeling for Breast Surgery Simulation

(6)

where

H is a matrix which consist of radial basis function values.

With the same steps above, we deform in the y-

and z-directions also. We apply RBF for all vertices

of template mesh data and finally get the morphed

data according to the subject.

Figure 6: Before and after local deformation from several

views (dot mark: , cross mark: ).

3.5 Texture Mapping

For realism, the texture image is mapped onto the

deformed mesh data. The subject’s front-view and

side-view images are used for texture mapping.

Because we have already assigned feature points on

the images, the texture coordinates of each vertex

are easily calculated. The main issue in texture

mapping is how to blend the three or four orthogonal

images. We checked the normal direction of facets

to decide the blending ratio. Here, let us assume that

we use front-, left- and right-view images for the

texture mapping. The front-view and side-view

images are orthogonal, so the blending ratio is

calculated by the normal vector’s Z component. At

this time, the left image should be used only for the

left part (x>0), and vice versa for the right part.

When we add the back-view image, the blending

algorithm is similar, too. Eq. (7) explains our texture

image blending method in detail.

if x>0 (i.e. left part),

if >0,

else

(7)

if x<0 (i.e. right part),

if <0,

else

where

: X and Z component of the normal vector, respectively

The normal vectors are normalized.

: the blending ratio of front, left and right images

for texture mapping, respectively.

Figure 7: The resulting 3D data from a subject’s

photographs: the geometrical shape (left) and the textured

model (right).

4 RESULTS

This paper proposes an image-based 3D torso

modeling method. A template data is prepared, and

the efficient number and positions of the feature

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

)(

)2(

)1(

zlzf

−

0,1

zrzf

−

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

points are verified. We have developed and applied

several geometric deforming algorithms and a

texture mapping method to get the subject’s 3D data

from images. We also have designed an image-

capturing device to approximate the actual size. We

can measure dimensions or volumes of a subject’s

data if we reconstruct the 3D data in actual size. The

remote-capturing function enables the operator to

take digital images handily. In Figure 8 shows the

result of our work compared to front-view photos.

As the figure indicates, both the 3D geometry and

texture information of each subject are reconstructed

well for the purpose of visualization.

We analyzed the results by comparing them to

the subjects’ actual 3D scan data. Table 2 shows

those results. RapidForm2002 was used to analysis

the distance errors (http://www.rapidform.com). The

errors are rather big due to the limitations of the

image-based approach. The different postures of the

subjects increased the errors. However, our result is

realistic enough to meet our original goal, which is

virtual simulation of breast surgery. Moreover, our

method requires only three orthogonal images and

needs no expensive hardware. It takes only about a

minute to get the results, starting from capturing a

subject’s photos. We are convinced that the

proposed method can be applied to animation or

other computer graphics with no problem.

To increase the proposed approach’s reliability,

some plastic surgeons and implant retail dealers

have participated and shared their know-how in the

development process.

5 FUTURE WORK

The final goal of this project is to develop a 3D

breast surgery simulation system; thus a new

algorithm is needed to deform a subject’s current 3D

model to see the virtually changed appearance after

the surgery. One possible method for this simulation

would be to use the displacement vectors of the

feature points between before and after the

operation. Our image-based 3D modeling algorithm

will be applied to get subject’s 3D data before and

after plastic surgery for the existing cases. The

relationship between before and after the operation

would be derived by synthesizing or averaging the

transform vectors. Then the deformed feature points

would be obtained from the relationship, and finally

the simulated 3D data would be obtained by

applying RBF interpolation. Because 3D data are

available only if the transformed feature points are

given, this scenario is plausible and reasonable. For

this purpose, we are gathering orthogonal images of

patients before and after plastic surgery. For realistic

simulations, it is also necessary to construct a

database of body shapes according to implant types

and sizes. It would be also possible to make other

cosmetic surgery simulation software for the face

and other parts of the body by extending the scenario

described above.

Figure 8: Examples of eight female subjects. Upper rows

are snapshots of the reconstructed 3D data, and lower rows

show real frontal photos of each subject.

Table 2: Distance errors between the reconstructed data

and the scanned data of the subjects. (unit: [㎜], SD:

standard deviation).

No. Min. Max. Mean SD

1 -14.2 15.3 0.05 5.41

2 -25.0 17.8 0.41 5.45

3 -14.6 20.6 0.57 5.72

4 -24.2 27.5 -0.87 9.23

5 -14.1 13.8 0.28 6.40

6 -19.0 25.5 1.57 7.87

7 -18.3 19.7 0.67 5.91

8 -15.7 13.8 -0.72 5.89

ACKNOWLEDGEMENTS

We would like to thank K&I Technology and

Woorhi Trading for their technical support. We also

appreciate Dr. SungJun Back and Dr. DongRak Lee

for their advice. This work is financially supported

by the Ministry of Education and Human Resources

Development (MOE), the Ministry of Commerce,

Industry and Energy (MOCIE) and the Ministry of

IMAGE-BASED 3D TORSO BODY MODELING - 3D Female Body Modeling for Breast Surgery Simulation

Labor (MOLAB) through the fostering project of the

Lab of Excellency. This research was also supported

in part by the Institute of Advanced Machinery and

Design at Seoul National University.

REFERENCES

W. Lee and N. Magnenat-Thalmann, 2000. Fast head

modeling for animation. Journal Image and Vision

Computing.

M. Zhang, el al., 2004. Image-Based 3D Face Modeling.

Proceeding of the International Conference on

CGIV’04.

R. Balaniuk, I. Costa and J. Melo, 2006. Cosmetic Breast

Surgery Simulation. VIII Symposium on Virtual

Reality - SVR2006.

W. Lee, J. Gu and N. Magnenat-Thalmann, 2000.

Generation Animatable 3D Virtual Humans from

Photographs. Computer Graphics Forum

(Eurographics 2000).

J.C. Gower and G.B. Dijksterhuis, 2004. Procrustes

Problems, Oxford University Press.

A.N. Ansari and M. Abdel-Mottaleb, 2003. 3-D Face

Modeling Using Two Views and a Generic Face

Model with Application to 3-D Face Recognition. In

Proceedings of the IEEE Conference on Advanced

Video and Signal Based Surveillance.

U. Neumann, el al., 1999. Constructing a Realistic Head

Animation Mesh for a Specific Person. USR-TR.

J.C. Carr, et al., 1997. Surface interpolation with radial

basis functions for medical imaging. IEEE

Transactions Medical Imaging.

D. Ruprecht and H. Müller, 1993. Free form deformation

with scattered data interpolation methods. Geometric

Modelling (Computing Supplement 8), Springer

Verlag., Wien.

R.Y. Tsai, 1987. A Versatile Camera Calibration

Technique for High-Accuracy 3D Machine Vision

Metrology Using Off-the-Shelf TV Cameras and Lens.

IEEE Journal of Robotics and Automation.

A. Hilton, D. Beresford, T. Gentils, R. Smith and W. Sun,

1999. Virtual People: Capturing Human Models to

Populate Virtual Worlds. Computer Animation,

Geneva, Switzerland.

T. Goto, W. Lee and N. Magnenat-Thalmann, 2002. Facial

feature extraction for quick 3D face modeling. Signal

processing: Image communication.

W. Lee, P. Kalra and N. Magnenat-Thalmann, 1997.

Model Based Face Reconstruction for Animation. In

Proc. Multimedia Modeling (MMM'97).

J. Noh, D. Fidaleo and U. Neumann, 2000. Animated

Deformations with Radial Basis Functions. ACM

Virtual Reality and Software Technology (VRST).

J.C. Carr, el al., 2001. Reconstruction and Representation

of 3D Objects with Radial Basis Functions. Annual

Conference Series.

I.K. Park, el al., 2005. Image-Based 3D Face Modeling

System. EURASIP Journal on applied signal

processing.

H. Lee, K. Hong and E. Kim, 2004. Measurement protocol

of women’s nude breasts using a 3D scanning

technique. Applied Ergonomics 35.

H. Seo, F. Cordier and K. Hong, 2007. A breast modeler

base on analysis of breast scans. Computer Animation

and Virtual Worlds 2007.

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications