
DETECTION OF FACES IN WIRE-FRAME POLYHEDRA
Interactive Modelling of Uniform Polyhedra
Hidetoshi Nonaka
Hokkaido University, N14W9, Sapporo, 060 0814, Japan
Keywords: Uniform polyhedron, polyhedral graph, simulated elasticity, interactive computing, recreational
mathematics.
Abstract: This paper presents an interactive modelling system of uniform polyhedra including regular polyhedra,
semi-regular polyhedra, and intersected concave polyhedra. In our system, user can virtually “make” and
“handle” them interactively. The coordinate of vertices are computed without the knowledge of faces, solids,
or metric information, but only with the isomorphic graph structure. After forming a wire-frame polyhedron,
the faces are detected semi-automatically through user-computer interaction. This system can be applied to
recreational mathematics, computer assisted education of the graph theory, and so on.
1 INTRODUCTION
This paper presents an interactive modelling system
of uniform polyhedra using simulated elasticity.
Uniform polyhedra include five regular polyhedra
(Platonic solids), thirteen semi-regular polyhedra
(Archimedean solids), and four regular concave
polyhedra (Kepler-Poinsot solids). Alan Holden is
describing in his writing, “The best way to learn
about these objects is to make them, next best to
handle them (Holden, 1971).” Traditionally, these
objects are made based on the shapes of faces or
solids. Development figures and a set of regular
polygons cut from card boards can be used to
assemble them. Kepler-Poinsot solids can be formed
by stellation of faces of “core” polyhedra.
“PolyFormes” is an application program for dialog-
based declarative modelling of polyhedra (Martin,
1999). These methods are based on faces. On the
other hand, some semi-regular polyhedra can be
formed by truncation of other solids. Kepler-Poinsot
solids can be also formed by faceting of solids of
“case” polyhedra. These methods are based on
solids (Coxeter, 1973).
In our system, user can virtually “make” and
“handle” all of the uniform polyhedra without the
knowledge of faces, solids, or metric information,
but only with the isomorphic graph structure. After
forming a wire-frame polyhedron with the vertices
and the edges, the faces are detected semi-
automatically through user-computer interaction.
2 UNIFORM POLYHEDRA
2.1 Platonic Solids
Five Platonic solids are listed in Table 1. The
symbol
n
m
P indicates that the number of faces
gathering around a vertex is n, and each face is m-
sided regular polygon.
Table 1: The list of Platonic solids.
Symbol Polyhedron Vertices Edges Faces
3
3
P Tetrahedron 4 6 4
3
4
P Cube 8 12 6
4
3
P
Octahedron 6 12 8
3
5
P Dodecahedron 20 30 12
5
3
P Icosahedron 12 30 20
Platonic solids, or regular solids, are convex
polyhedra with faces that are regular and congruent
polygons, while their vertices lie on the circum-
sphere, their vertex figures are also regular and
congruent.
2.2 Archimedean Solids
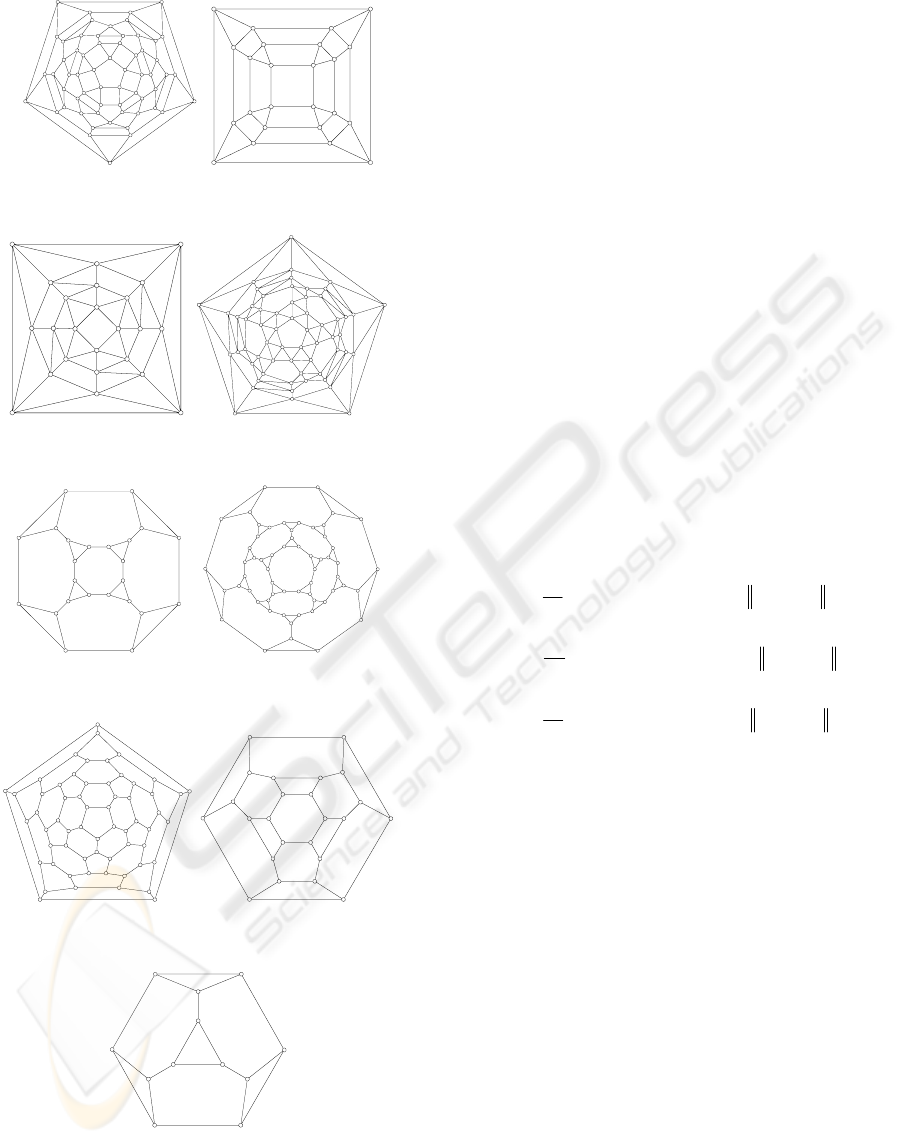
Thirteen Archimedean solids are shown in Figure 1.
Archimedean solids, or semi-regular solids, are
surrounded by several sorts of regular polygons, and
134
Nonaka H. (2008).
DETECTION OF FACES IN WIRE-FRAME POLYHEDRA - Interactive Modelling of Uniform Polyhedra.
In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 134-137
DOI: 10.5220/0001095301340137
Copyright
c
SciTePress

their vertex figures are not regular but congruent
polygons. Their vertices lie on the circum-sphere.
Some of Archimedean solids can be obtained by
truncation of other polyhedra.
2.3 Kepler-Poinsot Solids
Four Kepler-Poinsot solids are shown in Figure 2.
3
(5/2)
K (great stellated dodecahedron) and 5
(5/2)
K
(small stellated dodecahedron) are regular concave
polyhedra with pentagrams (5/2) as faces.
( a )
2
(3 4)
A
⋅
( b )
4610
A
⋅⋅
( c )
468
A
⋅⋅
( d )
2
(3 5)
A
⋅
( e )
3454
A
⋅⋅⋅
( f )
3
34
A
⋅
( g )
4
34
A
⋅
( h )
4
35
A
⋅
( i )
2
38
A
⋅
( j )
2
310
A
⋅
( k )
2
56
A
⋅
( l )
2
46
A
⋅
(m)
2
36
A
⋅
Figure 1: Thirteen Archimedean solids generated by the
system.
( a )
5/2
5
K
( b )
5/2
3
K
( c )
3
(5/2)
K ( d ) 5
(5/2)
K
Figure 2: Four Kepler-Poinsot solids generated by the
system.
3 POLYHEDRAL GRAPH
3.1 Polyhedral Graph
Drawing graph is the first step of polyhedron
modelling in the system. Polyhedral graphs
isomorphic to Archimedean solids are illustrated in
Figure 3-4. Kepler-Poinsot solids are isomorphic to
icosahedron or dodecahedron.
( a )
2
(3 4)
A
⋅
( b )
4610
A
⋅⋅
( c )
468
A
⋅⋅
( d )
2
(3 5)
A
⋅
Figure 3: Polyhedral graphs isomorphic to Archimedean
solids (1). (to be continued).
DETECTION OF FACES IN WIRE-FRAME POLYHEDRA - Interactive Modelling of Uniform Polyhedra
135
( e )
3454
A
⋅⋅⋅
( f )
3
34
A
⋅
( g )
4
34
A
⋅
( h )
4
35
A
⋅
( i )
2
38
A
⋅
( j )
2
310
A
⋅
( k )
2
56
A
⋅
( l )
2
46
A
⋅
(m)
2
36
A
⋅
Figure 4: Polyhedral graphs isomorphic to Archimedean
solids (2).
3.2 Simulated Elasticity
We define three binary relations between two
vertices:
The relation
adjacent corresponds to the length
of an edge in a 3 dimensional space. The relation
neighbour means that the length of path between
two vertices is 2, and two vertices are
neighbourhood of another vertex, and it corresponds
to the shape of vertex figure in a 3 dimensional
space. The relation
diameter corresponds to the
circum-sphere.
Virtual elastic forces are assumed between
vertices according to Hooke’s law and three
relations defined in the previous section. Let
,,
and
LLL be natural length of virtual spring, and
each lower suffix indicates “adjacent”, “neighbour”,
or “diameter”. Let
,,
and
kkk be spring constant,
which varies from 0 to 1. Bold-faced
,0, 1
i
ip=−v " stands for the 3 dimensional
coordinate of vertex
i
vV∈ . Then the total elastic
potential E
t
is given as follows:
tand
EEEE=++
(1)
()
()
()
2
(, )
2
(, )
2
(, )
2
2
2
ij
ij
ij
a
aaij
i j adj acent v v
n
nnij
ijneighbourvv
d
ddij
ijdiametervv
k
EL
k
EL
k
EL
<∧
<∧
<∧
⎧
⎪
⎪
=−−⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
=−−
⎨
⎪
⎪
⎪
⎪
⎪
⎪
=−−
⎪
⎪
⎪
⎪
⎩
∑
∑
∑
vv
vv
vv
4 DETECTION OF FACES
After constructing polyhedral graph, and arranging
vertices in 3-dimensional space using elastic
potential, the next step is detecting and selecting
faces. In the case of Platonic solids, Archimedean
solids, prisms, and anti-prisms, common routine is
available.
The faces of Kepler-Poinsot solid are detected
by separate routine. Selecting triangles from great
icosahedron is common with selecting triangles
from icosahedron. Selecting pentagrams from great
stellated dodecahedron is common with selecting
pentagons from dodecahedron. Lastly, selecting
pentagon from great dodecahedron is common with
selecting pentagram from small stellated
dodecahedron.
At this stage, the modelling of polyhedron is
completed. The final step is rendering the wire-
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
136
frame polyhedron with detected faces. In the case of
Kepler-Poinsot solids, faces are intersecting each
other. Then the process of hidden surface removal is
required. In the case of presented system, the target
machine is low cost PC with single CPU without
graphics accelerators. We tried to calculate the
geometric interference, and detected the exposed
fragments. As an example, such fragments in a
triangle of great icosahedron are obtained as is
shown in Figure 5, where shaded region is outside of
great icosahedron.
Let
,,, ,abc r"
be the position vector of each
point in the figure:
,,,,OA OB OC OR
JJJG
J
JJG JJJG JJJG
"
, then they
are expressed by
a and b as follows,
55 355
510
−−
=+ca b
,
51
2
−
=da
,
5525
55
−
=+ea b
,
35
2
−
=
f
a ,
55 355
10 10
−−
=+ga b. (5)
35 35
88
+−
=+pab,
1
2
=qa
135
48
−
=+ra b (6)
O
A
B
C
D
E
F
G
P
Q
R
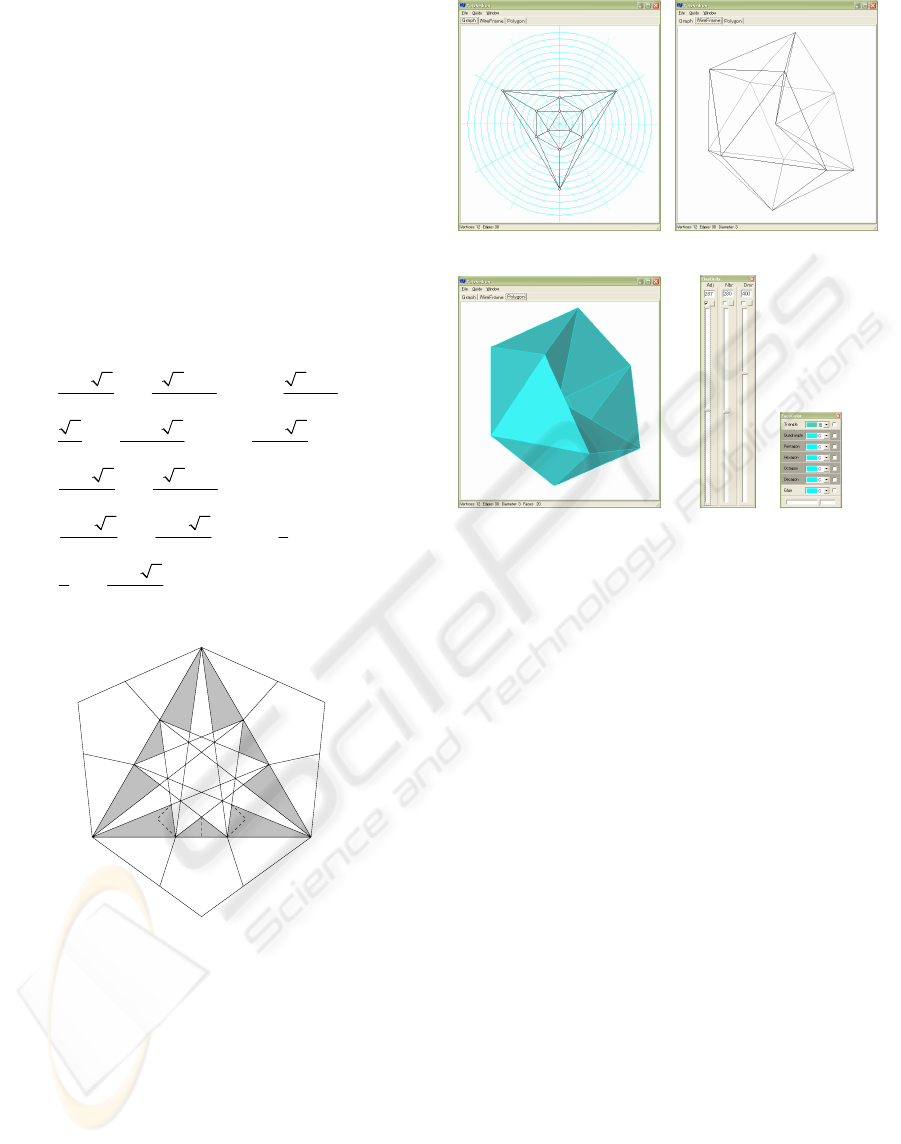
Figure 5: Nine exposed fragments of triangle OAB∆
surrounding the great icosahedron.
5 SYSTEM OVERVIEW
Figure 6 shows snapshots of GUI. In this example,
depressed icosahedron is obtained. It means the
elastic potential remains at a local minimum. It can
be recovered interactively by pulling a proper vertex,
or increasing the natural length of diameter, and so
on.
( a ) Graph input window ( b ) Wire-frame window
( c ) Polygon window ( d ) Control tools
Figure 6: Snapshots of GUI of the system.
6 CONCLUSIONS
This paper proposed an interactive modelling system
of uniform polyhedra. Process of modelling is
composed of following three steps. Firstly, a
polyhedral graph is constructed by editing graph
with several graph operations. Secondly, wire-frame
polyhedron is formed by simulated elasticity with
the relation of adjacent, neighbour, and diameter.
Lastly, proper faces are detected semi-automatically
through user-computer interaction. This system can
be applied to recreational mathematics, computer
assisted education of the graph theory, and so on.
REFERENCES
Coxeter, H. S. M., 1973. Regular Polytopes, Dover
Publications, New York.
Coxeter, H. S. M., 1999. The Beauty of Geometry, Twelve
Essays, Dover Publications, New York.
Holden, A., 1971. Shapes, Space, and Symmetry,
Columbia University Press, New York.
Martin, P. and Martin, D., 1999. PolyFormes: Software
for the declarative modelling of polyhedra, The Visual
Computer, 15 (2), 55-76.
DETECTION OF FACES IN WIRE-FRAME POLYHEDRA - Interactive Modelling of Uniform Polyhedra
137
