GENERIC BRDF SAMPLING
A Sampling Method for Global Illumination
Rosana Montes, Carlos Ure˜na, Rub´en Garc´ıa and Miguel Lastra
Dpt. Lenguajes y Sistemas Inform´aticos, E.T.S.I. Inform´atica y de Telecomunicaci´on, University of Granada, Spain
Keywords:
BRDF, Importance Sampling, Monte Carlo Integration, Global Illumination, Rendering, Path Tracing.
Abstract:
This paper introduces a new BRDF sampling method with reduced variance, which is based on a hierarchical
adaptive parameterless PDF. This PDF is based also on rejection sampling with a bounded average number of
trials, even in regions where the BRDF does exhibit high variations. Our algorithm works in an appropiate way
with both physical and analytical reflectance models. Reflected directions are sampled by using importance
sampling of the BRDF times the cosine term. This fact improves computation of reflected radiance when
Monte-Carlo integration is used in Global Illumination. Test images have been obtained by using a Monte-
Carlo rendering system, and they show reduced variance as compared with those obtained by other known
techniques.
1 INTRODUCTION
In Global Illumination software the Bidirectional Re-
flectance Distribution Function (BRDF) is used to de-
scribe how light is scattered at surfaces, and it de-
termines the appearance of objects. Many reflec-
tion models have been proposed which account for
real visual effects produced by object-to-object re-
flections, self-shadowing, retro-reflection, etc. Monte
Carlo (MC) algorithms, which rely on BRDF sam-
pling, include distributed ray tracing (Cook et al.,
1984), path tracing (Kajiya, 1986), bidirectional path
tracing (Lafortune and Willems, 1993), density es-
timation (Shirley et al., 1995) and photon mapping
(Jensen and Christensen, 1995).
Monte Carlo methods usually require a large num-
ber of rays to be traced through the scene. The direc-
tion of the rays follows a stochastic distribution which
depends on light sources, BRDFs and visual impor-
tance. A mayor challenge in incorporating complex
BRDFs into a Monte-Carlo-based global illumination
system is efficiency in sampling, however, complex
reflectance models have no corresponding sampling
strategies to use with.
In (Lawrence et al., 2004) a Monte-Carlo impor-
tance sampling technique was presented for general
analytic and measured BRDFs based on its factor-
ization. We have used factorized approximations of
those BRDFs in order to compare Lawrence approach
with ours.
This document presents a method to improve
Monte-Carlo random walks by applying impor-
tance sampling of BRDFs to reduce the variance
of the estimator. Reflected directions are generated
with a probability density function that is exactly
proportional to the BRDF times the cosine term.
For generality, we have sampled many parametric
BRDFs that are well-known in computer graphics:
for plastics the Phong model and its variants (Phong,
1975; Blinn, 1977; Lewis, 1993; Lafortune and
Willems, 1994) and (Schlick, 1993), for metals the
He model (He et al., 1991), Strauss (Strauss, 1990),
Minnaert Lunar reflectance (Minnaert, 1941), for
rough and polished surfaces based on Torrance’s mi-
crofacet representation (Maxwell et al., 1973; Cook
and Torrance, 1982; Poulin and Fournier, 1990) and
(Oren and Nayar, 1994). Anisotropy models (Ward,
1992; Ashikhmin and Shirley, 2000a; Ashikhmin
and Shirley, 2000b) are also considered. In fact our
representation makes no assumptions on the BRDF
model but the need for evaluating the function giving
two directions.
The rest of this document is organized con-
sidering: Section 2 gives an overview of current
techniques for sampling the BRDF and explains
how importance sampling works when Monte Carlo
integration is used. Section 3 provides details of
our algorithm which adaptively samples the BRDF.
Results and time-error analysis are given in Section 4.
Some discussion and ideas for future work conclude
the paper.
191
Montes R., Ureña C., García R. and Lastra M. (2008).
GENERIC BRDF SAMPLING - A Sampling Method for Global Illumination.
In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 191-198
DOI: 10.5220/0001095801910198
Copyright
c
 SciTePress

2 REFLECTANCE EQUATION
AND MONTE-CARLO
ESTIMATION
One of the main interests in Global Illumination relies
on the evaluation of the reflected radiance, by using
the reflectance equation:
L
r
(w
o
)
def
=
Z
Ω
f
r
(w
o
,w
i
)L
i
(w
i
)(w
i
·n)dσ(w
i
) (1)
Here L
i
stands for incoming radiance and L
r
for
reflected radiance. The above equation is usually
solved in global illumination by using MC integra-
tion, because it is often impossible to obtain analytic
expressions for L
r
or L
i
. Let w
o
= (u
x
,u
y
,u
z
) and
w
i
= (v
x
,v
y
,v
z
) be two unit-vectors in Ω, the hemi-
sphere of unit radius with n
def
= (0,0,1).
2.1 MC Numerical Estimation of L
r
Integration over the hemisphere Ω can be done by us-
ing three related measures defined in that domain: (1)
the solid angle measure (which we note as σ), (2) the
projected solid angle measure (σ
p
) and (3) an area
measure A.
(w· n)dσ(w) = dσ
p
(w) = dA(h(w)) (2)
Let D denote the unit radius disc in R
2
. By us-
ing equation (2), the reflectance equation (1) can be
alternatively expressed as:
L
r
(w
o
) =
Z
D
f
r
(w
o
,w
xy
)L
i
(w
xy
)dA(x,y) (3)
where w
xy
∈ D is the projection of w
i
onto D.
When numerical integration of an arbitrary
integrable (w.r.t. a measure µ) function g ∈ S → R
is done by using MC techniques, random samples
in S must be generated from a random variable with
probability measure P —which obeys P(S) = 1 and
it is absolutely continuous w.r.t µ—. The function
p
def
= dP/dµ is frequently called the probability
density function (PDF) of those samples. From n
such random samples (namely {x
1
,...,x
n
}) we can
build a new random variable (r.v.) X
n
whose mean
value is the integral I we want to compute. This is
done by generating samples sets whose PDF is p, and
evaluating X
n
on them. The variance of X
n
is a value
which determines the efficiency of the method.
Designing efficient MC sampling methods usually
means designing good PDFs by using all available
information about g. The closer p to g/I the less
variance we obtain (ideally p = g/I). Consider
now integrals like equation (1) and assume we have
no knowledge about irradiance or other terms of
the integrand, but with a known BRDF. In these
circumstances, the best option is to use a PDF which
is as proportional as possible to the BRDF times the
cosine term.
To compute an estimator of L
r
(w
o
), as defined in
equation (1), for a given w
o
∈ Ω, we must use a set
of samples (s
1
,...,s
n
), which are n identically dis-
tributed random vectors defined in Ω, with probabil-
ity measure P
w
o
(the probability measure depends on
w
o
). With this sample set, the estimator of the outgo-
ing radiance can be obtained as:
L
r
(w
o
) ≈
1
n
n
∑
k=1
f
r
(w
o
,s
k
)(s
k
· n)
q
w
o
(s
k
)
L
i
(s
k
) (4)
where q
w
o
= dP
w
o
/dσ is the PDF associated to P
w
o
.
An alternative expression can be given by us-
ing equation (3) instead of (1) and it’s used in
our algorithm. In this case, the set of samples
((x
1
,y
1
),...,(x
n
,y
n
)) contains random vectors in D
instead of in Ω, and the estimator becomes:
L
r
(w
o
) ≈
1
n
n
∑
k=1
f
r
(w
o
,s
k
)
p
w
o
(x
k
,y
k
)
L
i
(s
k
) (5)
where s
k
is the projection of (x
k
,y
k
) onto Ω.
In this case, the PDF p
w
o
= dP
w
o
/dσ
p
=
dP
w
o
/dA is defined w.r.t. area measure A, and its
domain is D. Finally, from equations (4) and (5) we
conclude that the PDF must be evaluated, and thus
we should be capable to do this in a short time.
2.2 Sampling the BRDF
2.2.1 Lobe Distribution Sampling
A well known class of BRDF models are based on
cosine-lobes, which have an associated algorithm for
sampling. Within this category are Phong, Blinn
and their respective normalized versions delivered by
Lewis, Lafortune and Ward. The single-lobe BRDF is
defined as:
f
r
(w
o
,w
i
) = C(n) (w
i
· w
o
r
)
n
where n ≥ 0 is a parameter, and C(n) is a normaliza-
tion factor which normally depends on n and ensures
these BRDFs obey conservation of energy.
For this BRDF, a related and normalized PDF can
be defined as:
p
w
o
(w
i
) =
1
N
1
(w
o
r
,n)
(w
i
· w
o
r
)
n
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
192

where N
1
ensures normalization and is defined as:
N
1
(a,n)
def
=
Z
Ω
(w
i
· a)
n
dσ(w
i
)
N
1
is called a single axis moment around axis a
and analytical expressions for it are known (Arvo,
1995).
In order to obtain samples distributed according to
this PDF, we obtain a random vector w
i
whose spher-
ical coordinates are:
(θ
wi
,φ
wi
) =

arccos

ξ
1
n+ 1
1

,2πξ
2

where ξ
1
and ξ
1
are two independent uniformly dis-
tributed random variables with values in [0,1).
A variant of this PDF avoids evaluation of N
1
by
using samples on the whole sphere S
2
, instead of only
the hemisphere Ω. Taking into account the part of the
lobe under the surface, it makes N
1
(w
o
,n) indepen-
dent of w
o
and equal to N
1
(n,n) = 2π/(n + 1). This
PDF is defined in the sphere, however, when a sample
is produced under the surface, the contribution of that
sample to the integral is taken as zero. The algorithm
is faster and still unbiased, but it has higher variance
when w
o
approaches grazing angles.
Cosine-lobe sampling is the most efficient sam-
pling for Phong BRDF and its variations but this
scheme is not suitable for non-lobe-based BRDFs.
2.2.2 The Factorized BRDF Representation
Recent work about effective importance sampling
strategies for arbitrary BRDFs is Lawrence’s factor-
ization of the BRDF (Lawrence et al., 2004). This
function is decomposed as the product of two 1D
functions, stored compactly in tabular form, and then
it is used for sampling.
A first factorization, after a reparametrization
based on the half angle, gives a decomposition into
2D factors of the initial data matrix Y containing
N
w
× N
wo
values along the outgoing elevation angle
and the outgoing azimuthal angle. After that, Y is ap-
proximated by the product of two matrices of lower
dimension: G is N
w
× J and F is an J × N
wo
matrix.
Both matrices are always positive by using the non-
negative matrix factorization (NMF) method (Lee and
Seung, 2000)
1
.
A second factorization of the view independent G
matrix leads to the product of two matrices of one di-
mension, very easy to sample by numerical inversion
of the Cumulative Distribution Function after normal-
ization.
1
Code sample is given by J. Lawrence in
< http://www.cs.virginia.edu/ jdl/nmf/ >.
f
r
(w
o
,w
i
) cos(w
i
) ≈
J
∑
j
F
j
(w
o
)
K
∑
k
u
jk
(θ
w
)v
jk
(φ
w
).
(6)
Each L = J × K factor is intuitively the approx-
imation of a specific lobe of the original BRDF.
When the factorization is used in generating random
directions two steps are necessary. First sampling
according to F selects one of the L lobes that
contributes more energy for the current view. The
CDF for this step is recomputed when the outgoing
direction changes. Next the hemisphere is sampled
according to selected lobe l by sequential generation
of elevation and azimuthal angles using pre-computed
CDF for factors u
l
and v
l
respectively.
3 OUR ALGORITHM
We consider the reflectance equation given in (3), and
the estimator in (5). The proposed sampling scheme
yields more samples in areas where the BRDF times
the cosine term has higher values, thus achieving im-
portance sampling. The usage of area measure A on
D is better than σ on Ω because this makes it unnec-
essary to include the cosine term in the formulation or
the computation, making the first simpler and the sec-
ond faster and more reliable. Also, the algorithm is
independent of the BRDF and avoids user guidance.
Our method is based on rejection sampling (Gen-
tle, 2003). This is a very simple and well known tech-
nique that yields a PDF proportional to any function
g ∈ G → R. It only requires that g can be evaluated,
and its maximum value m in G to be known. How-
ever, it runs a loop which in fact can be executed a
unbounded number of times, thus it potentially yields
large computing times even in the cases when g can
be quickly evaluated.
The probability for a sample to be accepted is e/m,
where e > 0 is the average value of g in the domain
G. The number of times the main loop is executed
(until a valid sample is obtained) is a geometric dis-
tribution with success probability e/m, and thus the
average number of trials is m/e, which can be quite
large for e ≪ m.
The core of our approach is an hierarchical
quadtree structure which can be used to efficiently
obtain samples with a PDF exactly proportional to
the target function. The adaptive approach checks
whether a region can be safely used for raw rejection
sampling. This check consists on evaluating, for that
region, the average number n
t
of trials with rejection
sampling in that region. This can be known provided
we know both e and m for the region. If n
t
is above a
GENERIC BRDF SAMPLING - A Sampling Method for Global Illumination
193

threshold number n
max
, then the region is subdivided
in four, and the criterion is applied to these four
subregions. Otherwise, the region is not subdivided.
If we apply this recursive process starting from D (the
unit radius disc centered at the origin), we obtain a
quadtree which can be used to efficiently sample the
BRDF. In the next section, further details are given
about this process.
3.1 Building the Adaptive Structures
As the sampling process requires a PDF proportional
to f
r
(w
o
,·) for arbitrary values of w
o
and for a finite
collection of BRDFs in a scene, it is necessary to cre-
ate a quadtree structure that subdivides the unit disc
domain for each ( f
r
,w
o
) pair. In the case of w
o
, a
finite set of vectors S = {w
1
,...,w
n
} can be used.
When an arbitrary w
o
is given, it is necessary to se-
lect the nearest w
j
to w
o
and use the corresponding
structure. The error induced by using w
j
instead of
w
o
can be reduced by using a large n and uniformly
distributing vectors w
j
. Note that, since we assume
the BRDF to be isotropic, it is enough for S to include
vectors in the plane XZ, thus a rotation must be ap-
plied to w
o
before finding the nearest w
j
. The inverse
rotation must be applied to resulting samples.
For a given quadtree in this structure, each node i
has an associated region R
i
⊆ D, which it is a square
area defined by:
R
i
= [u
i
,u
i
+ s
i
) × [v
i
,v
i
+ s
i
)
where (u
i
,v
i
) is the lower left vertex of the region
boundary and s
i
is the edge length. The region as-
sociated to the root node is the full domain [0,1)
2
.
The algorithm creates the root node and it checks
the criteria for subdivision. If the split is necessary,
four new child nodes are created, each one with an
associated region with a edge length size half of that
of the parent. Then, process is recursively applied to
these new four nodes. The recursive algorithm ends
in case no split is necessary or a predefined maximal
depth is reached.
In order to check the subdivision criteria for node
i these values must be computed:
M
i
= max{ f
r
(w
o
,w
i
xy
) | (x, y) ∈ R
i
}
I
i
=
Z
R
i
f
r
(w
o
,w
i
xy
)dA(x,y)
V
i
= s
2
i
M
i
M
i
is the smaller upper bound for values of f
r
in the
i-th region, I
i
is the integral of the BRDF in the re-
gion andV
i
is the volume of the space where rejection
sampling is done. Both M
i
and I
i
can be computed
by evaluating f
r
on a very dense grid of points in R
i
creating the quadtree, or alternatively a bottom-up ap-
proach could be used which starts by obtaining these
values at the maximum depth possible (with a high
resolution grid) and then it stores them so the data can
be used during tree construction. Therefore, the algo-
rithm only requires to be able to evaluate the BRDF.
In any case, it holds that the sum of the I
i
values for
the four children of a parent node must be equal to
that value on the parent.
The subdivision criteria used must ensure that re-
jection sampling on leaf nodes can be done with an
a priori bounded number of average trials n
max
. This
can be easily ensuring that:
n
max
I
i
V
i
≥ 1 (7)
where the probability for accepting a sample is I
i
/V
i
.
When this inequality does not holds, the node
must be split. In our implementation, we have used
n
max
= 2. The larger n
max
the less memory that is
needed (because the quadtree has smaller depth) and
the less time is used for quadtree traversal, but more
time is needed for rejection sampling on leaf nodes.
3.2 Obtaining Sample Directions
Generating a random direction involves selecting a
leaf node and then doing rejection sampling on that
node. If the i-th node is a leaf node, then the proba-
bility for selecting it must be proportional to I
i
(more
exactly it is I
i
/I
0
, if we assume the root node has in-
dex 0). A leaf node is selected following a path from
the root to the leaf. On each step, starting from the
root, the integrals I
i
of the descendants nodes are used
for randomly choosing one child to continue the path
down.
To do this, we can store in each node i four values
F
i0
,...,F
i3
, defined as:
F
ik
=
∑
k
j=0
I
C
ij
∑
3
j=0
I
C
ij
where C
ij
is the index of i-th node j-th child node
(note that F
i3
= 1). Leaf selection is then simply a
loop:
Algorithm 1
LeafNodeSelection( )
i := 0 (index of root node)
while i-th node is not a leaf do begin
r := uniform random value in [0,1)
j := min. natural such that r < F
ij
i := j
end
return i
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
194

Rejection sampling on the resulting i-th node is car-
ried out. This consists in selecting a random vector
(x,y,z) ⊆ R
3
with uniform distribution in the prism
R
i
× [0,M
i
]. Value z =
p
x
2
+ y
2
is then obtained
and the condition f
r
(w
o
,w
xy
) < z is checked. If it
holds,w
xy
is returned as the resulting sample, other-
wise a new sample must be generated and checked. A
sample is valid with probability I
i
/V
i
, which is neces-
sarily greater than 1/n
max
, because of inequality (7).
With our method samples on the disc will follow
a distribution where more samples are placed in parts
of the domain where the function has higher values.
In fact, it is exactly proportional to the BRDF.
Figure 1: Both images show a distribution of 2500 samples
obtained with our disc method. The left one shows how the
samples match the BRDF function (in red). The image on
the right is the projection on disc of those directions.
3.3 Quadtree Traversing for Optimal
Sampling
Some considerations should be taken in order to in-
crease the time performance. For example rather than
asking for a single sample s
i
we can implement a sin-
gle recursive traversal algorithm which yields a set of
n samples. Each node is visited once at most, instead
of visiting it n times as it would be the case when us-
ing the basic approach we introduced.
First the algorithm starts by requesting n samples
in the root node region and proceeding recursively.
Whenever a node with index i is visited, the program
must produce t random samples in R
i
. If the i-th node
is a leaf, those t samples are obtained by rejection
sampling. When i-th node is an inner node, a parti-
tion of t is done, selecting four random integer values
m
i,0
,...,m
i,3
, which hold m
i,0
+ m
i,1
+ m
i,2
+ m
i,3
= t
and in such a way that the average value of m
i, j
is
nI
C(i, j)
/I
i
. Then the algorithm is recursively called
for each j-th childC(i, j) of i-th node (this is not done
if m
i, j
= 0), and as a result we obtain four sets with t
samples in total. These four sets can be joined in one,
which is the resulting set of t samples. Each leaf node
j contains nI
i
/I
0
samples on the average, as required
by importance sampling.
4 RESULTS
In this section we provide results for our adaptive
sampling method for various reflectance models, and
we compare the computing time and average rela-
tive error we obtain for several images under different
sampling strategies (PDFs).
We have analyzed different PDF functions (in-
cluding the one we present) and we have measured
their performance for various BRDFs models when
high variation occurs, for instance, at a specular peak.
Images have been obtained with a varying number of
samples per pixel ranging from 1 sample, 5
2
, 10
2
, 15
2
,
20
2
, 30
2
, 40
2
, 50
2
and 1000
2
samples. The maximum
quality (1000
2
samples) has been used to produce a
reference image. We assign to each image a relative
error value, computed with respect to this reference
image. We average relative error for all pixels with
non-null radiance in the reference image and report it
as a percentage.
The full set of images takes each BRDF function
from a list of the most common theoretical and
empirical models (table 2) and samples them with
the following five PDFs: (1) uniform sampling
technique, (2) cosine lobe sampling on S
2
and Ω, (3)
Lawrence’s factorization (Lawrence et al., 2004) and
(4) the proposed adaptive method. All the images
were rendered using a naive path tracing algorithm in
a Linux machine with an AMD64 processor and 2GB
of RAM.
Figure 2: Rendering image example of the test scene.
4.1 Glossy Sphere
Considering a sphere object lit by a single area light,
as shown in Figure 2. We focused our measures on
the portion of the image containing the highlight on
the sphere, because in that portion is where efficiency
of different sampling approaches differs the most.
Each PDF model, with exception of uniform sam-
pling and our method, is assigned a set of manu-
ally adjusted parameters in order to match the target
GENERIC BRDF SAMPLING - A Sampling Method for Global Illumination
195

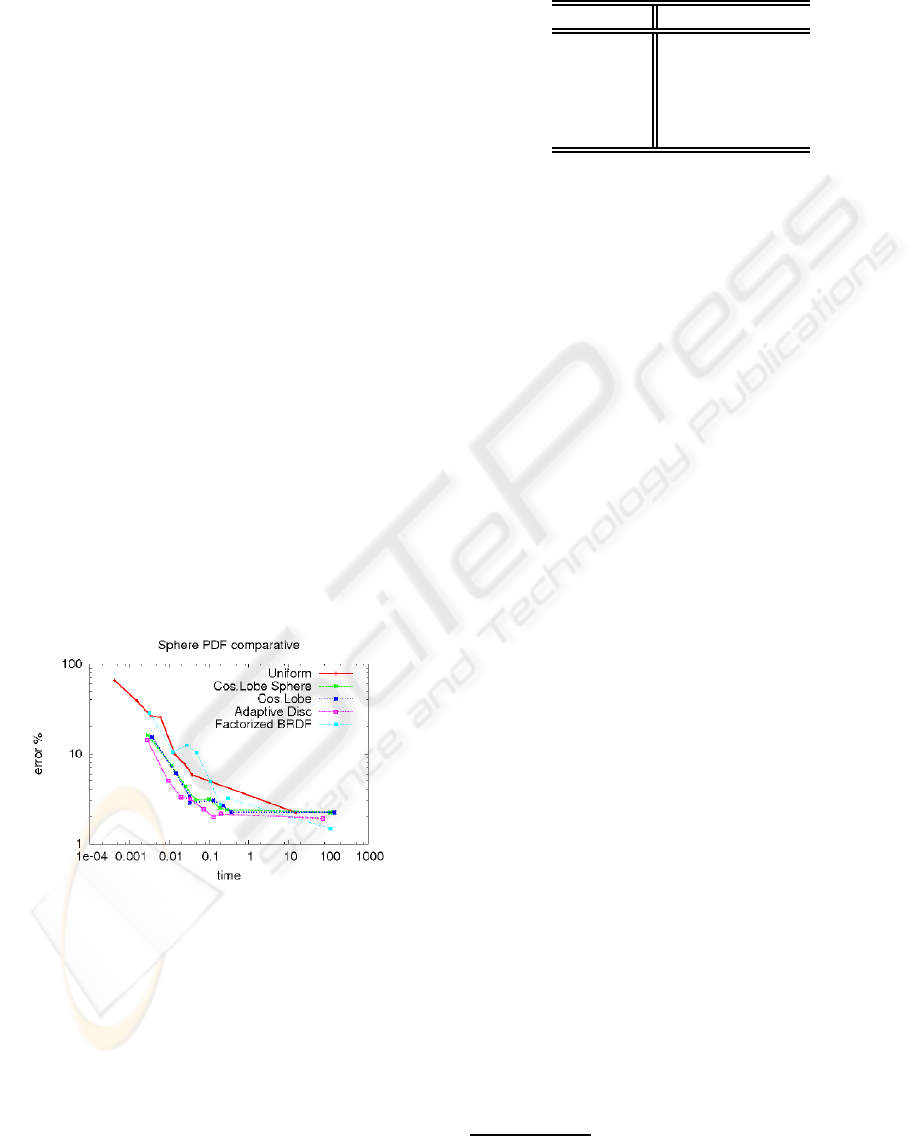
BRDF. For example, a cosine-lobe based PDF uses an
exponent parameter n. This value could be taken from
the corresponding exponent in the BRDF in use, how-
ever, there is no information to set the PDFs exponent
if we sample a BRDF model which does not depend
on that parameter, thus a constant must be used. To
make comparisons fairer we have manually found the
exponent that yields the best match between the lobe-
based PDF and each BRDF function. Even for Phong-
based BRDFs, the best n for the PDF can be differ-
ent to the BRDFs exponent. This is because both the
PDF and the BRDF include the term (w
o
· w
i
)
n
, how-
ever the BRDF also includes the cosine term (w
i
· n)
whereas the PDF does not.
For the Factored PDF we have found the best fac-
torization. It is necessary to find seven values for each
BRDF. Parameters are: N
θ
wo
×N
φ
wo
and N
θ
p
×N
φ
p
for
matrix size, J × K for the numbers of lobes that ap-
proximates the BRDF and whether or not to use the
half-angle reparametrization. Best values are found
comparing the average original matrix value with the
average from the product of factors.
To compare the various PDF functions we plot the
sampling time obtained vs. non-null pixel averaged
relative error. By considering this, we can select the
best method as the one that gives less error for a given
time. The results are plotted in Figure 3. Numerical
data is given in Table 1.
Figure 3: PDF comparative for Sphere scene. Manual se-
lection of the cosine lobe exponent is needed, as well as the
best factorization has to be found.
As the graph shows, the plot of our method is in
most cases below the others. This means that, with
same time our sampling performed best and also with
same error our method needs less time. The adaptive
method not only can be used with any isotropic BRDF
but it also does not need manual selection of parame-
ters, and it requires no knowledge of the BRDF. It just
requires the ability to evaluate the BRDF.
Table 1: Relative error and average sampling time in sec-
onds for each PDF and test scene when 50
2
samples are
taken compared to the 1000
2
sample reference image.
error time
Uniform 5.82% 0.03792
C.Lobe S
2
2.39% 0.28328
C.Lobe Ω 2.24% 0.35734
Adaptive 2.13% 0.20032
Factored 3.19% 0.2986
4.2 Sampling many BRDFs
In this point we treat on the Dragon model from the
Stanford University
2
. The reflectance function used
in this scene corresponds to Oren’s (Oren and Nayar,
1994) with a rough value of 0.83, and a Strauss in-
stance (Strauss, 1990) mostly smooth for floor and
wall respectively. The dragon itself has a Lafor-
tune BRDF (Lafortune and Willems, 1994) with ex-
ponent n = 20. With this mixture of BRDFs, visu-
ally we can compare our sampling method with uni-
form sampling, cosine lobe in Ω, and the Factored
representation of Lawrence, with manually adjusted
parametrization to fit the shape of each BRDF in-
stance. With only 100 samples, our algorithm gives
results with less noise than the others. You can see in
Figure 4.
4.3 Quadtree Set Construction
Requirements
It was mentioned previously that our algorithm in-
volves some more computations in order to closely
represent any BRDF function. Table 2 shows in-
formation related to the cost in seconds of the pre-
computation for a given number of quadtree struc-
tures and varying incident angle directions. Once we
have these structures on memory, they are used to es-
timate radiance. The values that are listed in the table
correspond to the pre-computation of 90 quadtrees,
which is high enough to ensure a structure is available
very close to any incident direction. Average value is
20.71 seconds compared with 51.27, the cost of fac-
torized computationand pre-computationof CDFs for
sampling by using Lawrence’s technique. Also you
may notice the extreme difference in terms of time
between experimental and physically based reflection
models.
Another issue concerning the requirements of our
method is memory consumption. Let us consider
2
The Stanford 3D Scanning Repository at
< http://graphics.stanford.edu/data/3Dscanrep/ >
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
196

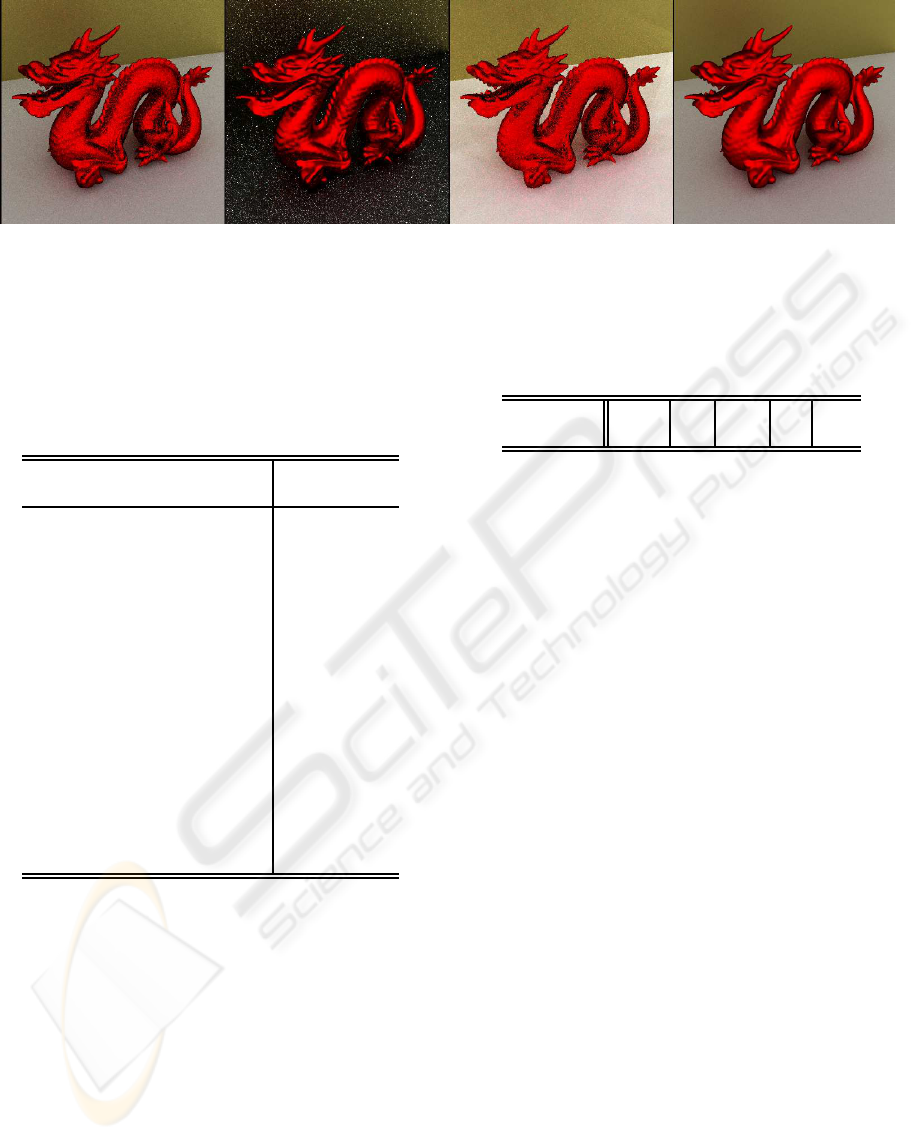
Figure 4: From left to right, images corresponding to uniform PDF, adjusted cosine-lobe strategy in Ω, the Factored represen-
tation of the BRDF and finally our algorithm sampling. Adaptive Disc shows less noise using the same number of samples
than the others. The resolution is 400 x 400 pixels. Following the same order, sampling time is: 9.232, 114.735, 90.028 and
133.172 seconds respectively.
Table 2: Quadtree creation times for each BRDF model
for Adaptive method compare with factorization and pre-
computation times of Factored PDF. Memory requirements
for both methods are also given. Data is relative to the
glossy scene.
BRDF
Adaptive Factorized
(sec) (KB) (sec) (KB)
Ashikhmin 51.4 6.25 82.9 1031
BeardMax. 15.5 1713.25 17.3 6454
Blinn 8.7 582.25 83.7 6481
Coupled 22.6 6.25 22.2 1033
He 102.7 2407.25 75.1 1034
Lafortune 6.6 1275.25 53.2 6445
Lewis 6.9 1279.25 119.3 6445
Minnaert 7.3 1461.25 4.9 1031
Oren 10.5 6.25 8.5 1033
Phong 6.9 1279.25 9.2 6445
Poulin 35.5 297.25 5.4 1038
SchlickD 19.1 342.25 77.9 1033
SchlickS 13.2 780.25 26.5 1043
Strauss 10.9 727.25 59.3 1052
Torrance 8.3 631.25 122.0 1029
Ward 20.7 483.25 51.3 1038
firstly our basic algorithm with no optimizations. A
single quadtree represents the unit disc domain as
node regions given an incident direction. Its depth,
and so its memory, depends on the nmax parameter
(see equation 7). Table 3 shows the cost of a single
quadtree when the nmax param changes. Memory
increments when many quadtrees are calculated and
stored. Table 2 shows the cost in KB for 90 quadtrees
and for each BRDF taking nmax as 2. Avarage value
of our method is 0.81 MB compared with 2.67 MB
of the factorized BRDF.
Table 3: Memory in KBytes for Adaptive Disc using θ
wo
=
74
◦
.
Disc
nmax 1.3 1.6 2 2.3 2.6
KB 2056.5 543 12.51 4.6 3.33
5 CONCLUSIONS
We have presented a new sampling method based on
an adaptive and parameterless algorithm which imple-
ments a PDF exactly proportional to generic BRDF.
Reflected directions were sampled using importance
sampling of the BRDF times the cosine term which
is preferable to only sampling the BRDF. The method
can be used for numerical Monte-Carlo based inte-
gration in global illumination or in other contexts. Its
efficiency is similar or even better than standard sam-
pling methods with manually selected optimal param-
eter values.
We also tested our adaptive sampling method
with tabulated BRDF representations (Matusik et al.,
2003) since they can be evaluated. We further plan to
develop, as future work, a method to acquire BRDF
data from an inexpensive 3D scanner, as a way to deal
with real world materials. We also plan to further re-
duce both sampling time and quadtree construction
time by using more optimized sequential programs,
SIMD instructions sets or parallel graphics hardware.
ACKNOWLEDGEMENTS
Special thanks to Francisco Javier Melero for his con-
tribution on this work. This work has been supported
by a grant coded as TIN2004-07672-C03-02 of the
Spanish Ministry of Education and Science.
GENERIC BRDF SAMPLING - A Sampling Method for Global Illumination
197

REFERENCES
Arvo, J. (1995). Applications of irradiance tensors to the
simulation of non-lambertian phenomena. In SIG-
GRAPH 1995 Proceedings, pages 335–342. ACM
Press.
Ashikhmin, M. and Shirley, P. (2000a). An anisotropic
phong brdf model. J. Graph. Tools, 5(2):25–32.
Ashikhmin, M. and Shirley, P. (2000b). A microfacet-based
brdf generator. In SIGGRAPH 2000 Proceedings.
Blinn, J. F. (1977). Models of light reflection for computer
synthesized pictures. In SIGGRAPH 1977 Proceed-
ings, pages 192–198. ACM Press.
Cook, R. and Torrance, K. (1982). A reflectance model for
computer graphics. In SIGGRAPH’81 Proceedings,
volume 1, pages 7–24. ACM Press.
Cook, R. L., Porter, T., and Carpenter, L. (1984). Dis-
tributed ray tracing. In SIGGRAPH’84 Proceedings,
pages 137–145, New York, NY, USA. ACM Press.
Gentle, J. E. (2003). Random number generation and Monte
Carlo methods. (2nd ed.). Springer.
He, X., Torrance, K., Sillion, F., and Greenberg, D. (1991).
A comprehensive physical model for light reflection.
In SIGGRAPH 1991 Proceedings, pages 175–186.
ACM Press.
Jensen, H. W. and Christensen, N. (1995). Photon maps
in bidirectional monte carlo ray tracing for complex
objects. In Computer & Graphics, number 2, pages
215–224.
Kajiya, J. T. (1986). The rendering equation. In SIGGRAPH
’86 Proceedings, pages 143–150. ACM Press.
Lafortune, E. P. and Willems, Y. D. (1993). Bi-directional
path tracing. In Proceedings of CompuGraphics,
Alvor, Portugal, pages 145–153.
Lafortune, E. P. and Willems, Y. D. (1994). Using the modi-
fied phong reflectance model for physically based ren-
dering. Technical Report Report CW197, Department
of Computer Science, K.U.Leuven.
Lawrence, J., Rusinkiewicz, S., and Ramamoorthi, R.
(2004). Efficient brdf important sampling using a fac-
tored representation. In ACM Transaction of Graph-
ics. Siggraph 2004, number 3, pages 496–505.
Lee, D. and Seung, H. (2000). Algorithms for non-negative
matrix factorization. In NIPS, pages 556–562.
Lewis, R. R. (1993). Making shaders more physically plau-
sible. In Eurographics Workshop on Rendering, pages
47–62, Vancouver, BC, Canada.
Matusik, W., Pfister, H., Brand, M., and McMillan, L.
(2003). A data-driven reflectance model. ACM Trans.
Graph., 22(3):759–769.
Maxwell, J. R., Beard, J., Weiner, S., and Ladd, D. (1973).
Bidirectional reflectance model validation and utiliza-
tion. Technical report, AFAL–TR–73–303. ERIM.
Minnaert, M. (1941). The reciprocity principle in lunar pho-
tometry. Astrophysical Journal, pages 403–410.
Oren, M. and Nayar, S. (1994). Generalization of lambert’s
reflectance model. In SIGGRAPH 1994 Proceedings,
pages 239–246, New York, NY, USA. ACM Press.
Phong, B.-T. (1975). Illumination for computer generated
pictures. In ACM Siggraph’75 Conference Proceed-
ings, number 6, pages 311–317, New York, NY, USA.
ACM Press.
Poulin, P. and Fournier, A. (1990). A model for anisotropic
reflection. In SIGGRAPH 1990 Proceedings, num-
ber 4, pages 273–282, New York, NY, USA. ACM
Press.
Schlick, C. (1993). A customizable reflectance model for
everyday rendering. In Eurographics Workshop on
Rendering, pages 73–84.
Shirley, P., Bretton, W., and Greenberg, D. (1995). Global
illumination via density-estimation radiosity. In Euro-
graphics Workshop on Rendering.
Strauss, P. S. (1990). A realistic lighting model for
computer animators. IEEE Comput. Graph. Appl.,
10(6):56–64.
Ward, G. J. (1992). Measuring and modelling anisotropic
reflection. In ACM Siggraph’92 Conference Proceed-
ings, number 4, pages 265–272.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
198