MESH

SIMPLIFICATION USING DISTANCE LABELS FOR

VIEW-INDEPENDENT SILHOUETTE PRESERVATION

Susana Mata, Luis Pastor

Dept. de Arquitectura y Tecnolog

ıa de Computadores, Ciencias de la Computaci

on e Inteligencia Artiﬁcial

C. Tulip

an, s/n., 28933 M

ostoles, Madrid, Spain

Angel Rodr

ıguez

Dept. de Tecnolog

ıa Fot

onica, U. Polit

ecnica de Madrid

Campus de Montegancedo s/n, 28660 Boadilla del Monte, Spain

Keywords:

Computational Geometry and Object Modelling, Three Dimensional Graphics and Realism, Picture and Image

Generation.

Abstract:

Multiresolution modelling is a good method to achieve both quality and performance in the rendering of com-

plex scenes. Within this framework, the detection and preservation of outstanding features, such us silhouettes,

become very important. The goal of this paper is to present a technique based on Distance Transforms that

allows to classify the elements of the mesh according to their proximity to both the internal and the external

contours and makes use of this information for weighting the approximation error which will be tolerated dur-

ing the mesh simpliﬁcation process. The approach used in this work precomputes silhouettes for a given set

of cameras and performs an estimation for any other point of view. The results obtained are evaluated in two

ways: visually and using an objective metric that measures the geometrical difference between two polygonal

meshes.

1 INTRODUCTION

Highly detailed polygonal meshes may contribute

to the generation of realistic renderings and physi-

cal simulations; however the high computation time

requirements may avoid ﬂuent interactivity, result-

ing paradoxically in a reduction of realism. Con-

sequently, whenever computation time is a concern,

techniques which decrease the model’s polygon count

while keeping an acceptable visual appearance are de-

sirable.

Multiresolution modelling presents itself as a suit-

able solution by representing objects at different res-

olution levels and choosing the proper approxima-

tion according to the visualization conditions (Xia and

Varshney, 1996; Hoppe, 1997). Basic principles of

this approach were set by James Clark (Clark, 1976);

comprehensive surveys can be found at (Puppo and

Scopigno, 1997; Garland, 1999; Luebke, 2001; Lue-

bke et al., 2003; De Floriani et al., 2005). Within

this framework, the detection and preservation of fea-

tures that drive the observer’s attention become cru-

cial . Silhouettes constitute an example of such fea-

tures, since they are known to be critical for the ﬁnal

visual quality appreciated by our visual system (Lue-

bke and Erikson, 1997).

The goal of this paper is to propose a new tech-

nique that allows taking into account the proximity of

a mesh element to the mesh’s contour for weighting

the approximation error which will be tolerated dur-

ing the simpliﬁcation process. More speciﬁcally, the

contributions of this work can be brieﬂy summarized

as follows:

• Applying a Distance Transform for detecting the

proximity of mesh elements to the silhouette for a

set of points of view.

• Extending the detection technique in order to in-

clude internal silhouettes.

• Using the precomputed proximity measure as an

error tolerance map in order to guide a simpliﬁca-

tion technique.

• Interpolating the proximity to the silhouette for a

new point of view not considered in the precom-

puted set of cameras.

The rest of the paper is organized as follows:

Section 2 presents a short overview of some previ-

ous work related to mesh simpliﬁcation algorithms

and the different approaches to identify and preserve

Mata S., Pastor L. and Rodríguez A. (2008).

MESH SIMPLIFICATION USING DISTANCE LABELS FOR VIEW-INDEPENDENT SILHOUETTE PRESERVATION.

In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 5-14

DOI: 10.5220/0001096300050014

 SciTePress

the model’s silhouette. A brief introduction to basic

concepts of digital Distance Transforms and Multi-

Tessellation is also included. Section 3 describes the

proposed approach, while Section 4 shows some ex-

perimental results. Finally the conclusions and future

work are presented in Section 5.

2 PREVIOUS WORK

2.1 Mesh Simpliﬁcation

Many mesh simpliﬁcation techniques have been pro-

posed during the last years. Among the methods

based on objective metrics, work has been done in or-

der to incorporate other attributes besides geometry

like color, texture or normals (Garland and Heckbert,

1998; Cohen et al., 1998). Perceptual metrics have

also been developed (O’Sullivan et al., 2004; Cheng

and Boulanger, 2005); Lindstrom and Turk use an im-

age metric to guide the simpliﬁcation process (Lind-

strom and Turk, 2000). Reddy introduced a percep-

tive model to guide the selection of the appropriate

level of detail (Reddy, 1997). (Luebke, 1998) de-

ﬁned a contrast sensitivity function that predicts the

perception of visual stimuli. Some of the perceptu-

ally driven simpliﬁcation methods explicitly pursue a

good silhouette preservation, deﬁning normal cones

(Williams et al., 2003). Good silhouette approxi-

mation through contour computation in image space

has also been researched (Raskar and Cohen, 1999;

Sander et al., 2000).

The approach presented here not only identiﬁes

the objects’ silhouette. It also performs an explicit

classiﬁcation of the mesh’s elements in object space,

depending on their proximity to the contour from a

given point of view.

The ﬁnal goal of a simpliﬁcation process may be

either to obtain a discrete set of simpliﬁed models or

to create a continuous multiresolution model. In this

last case, a hierarchical data structure is created in a

preprocessing stage and will be queried at run time

in order to extract the desired level of detail (Hoppe,

1997; De Floriani et al., 1997).

The Multi-Tessellation method, originally called

Multi-Triangulation, was introduced by De Floriani

et al. (De Floriani et al., 1997). It provides a general

multiresolution framework for polygonal meshes of-

fering several attractive features like selective reﬁne-

ment, locality or dynamic update (De Floriani et al.,

1998). The Multi-Tessellation, MT for short, is a hi-

erarchical model that can be generated during an off-

line simpliﬁcation process and queried at run time

for extracting a simpliﬁed mesh fulﬁlling some de-

ﬁned restrictions. Some useful restrictions are already

implemented in the distributed package (Geometric

Modeling and Computer Graphics Research Group,

2005), while the implementation of new ones can be

easily done.

The MT package has been used in this work for

implementing the extraction of a simpliﬁed model

that takes into account the visual relevance of a model

region. Its ﬂexibility and implementation conve-

nience have been some of the underlying reasons for

this choice.

2.2 Digital Distance Transforms

Measuring the distance between image elements may

be of interest for further processing in many image

analysis applications. Basics concepts regarding dig-

ital distances can be found in (Rosenfeld and Pfaltz,

1966; Rosenfeld and Pfaltz, 1968; Borgefors, 1984).

The application of a Distance Transform to a

binary image produces as output a distance image

where each element of this distance-image is assigned

a distance label. For any element its label stores

a value indicating its closest distance to the back-

ground. Therefore, the computed distance image can

be seen as a grey-level image where the intensity level

identiﬁes the minimum distance to the complement of

the object.

A distance transform can be computed in two

steps by propagating local distances over the image;

this is true for 2D, 3D and higher dimensions (Rosen-

feld and Pfaltz, 1966). Initially, the elements belong-

ing to the object are set to inﬁnity and the elements

belonging to the background are set to 0. In the case

of a 2D image, during the ﬁrst step the image is ana-

lyzed from top to bottom and from left to right. Dur-

ing the second step, the image elements are visited

from right to left and from bottom to top. Each el-

ement is assigned the minimum value between itself

and the already visited neighbors incremented by their

connectivity weight.

Distance transforms and some variations of them

in combination with other image processing tech-

niques can be applied for representing and analyzing

3D objects in multiple applications (Nystr

om, 1997;

Svensson, 2001; Sintorn, 2005; Jones et al., 2006).

Distance ﬁelds have also been applied in computer

graphics environments, such as in collision detection

(Teschner et al., 2004), and have been implemented

with graphics hardware (Sud et al., 2006).

However, digital distance transforms can be used

in other ﬁelds that have not been explored so far. The

work presented here aims to open a way for new ap-

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

plications of Distance Transforms within computer

graphics environments.

3 METHOD DESCRIPTION

The approach followed here classiﬁes the mesh faces

or vertices according to their proximity to the silhou-

ette, as seen from a speciﬁc point of view. The classi-

ﬁcation process uses a Distance Transform, computed

over the mesh elements’ projection on the visualiza-

tion plane. This transform provides for each element

its distance to the projected contour, being useful for

extracting the mesh elements which compose or are

located near the mesh silhouette for a particular point

of view. The distance of the mesh elements to the

projected contour (measured in image space) is en-

coded as distance-labels which are assigned to the

mesh, producing this way a view-dependent tagged

mesh.

If this process is applied for a number NC of cam-

eras, it will produce NC collections of precomputed

distance-labels, one collection for each camera. Since

these precomputed distance-labels are only valid for

the point of view from which they were extracted, an

interpolation technique is applied for any other point

of view.

The tags of the polygonal mesh elements, either

assigned or interpolated, can then be used in different

ways to guide the simpliﬁcation process, providing a

criterion for modifying locally the approximation er-

ror allowed in areas close to the contour.

It must be highlighted that the computation of

distance-labels for a set of cameras is performed in a

pre-processing stage, producing a set of labels which

will be used later on during the simpliﬁcation stage.

Figure 1 depicts a scheme of the whole process and

Alg. 1 collects its pseudo-code description. The fol-

lowing Sections describe each of the method’s stages.

3.1 View-dependent Distance Labels

Computation

Silhouettes are view-dependent features. For that rea-

son, their extraction must be done from a certain point

of view. This method’s ﬁrst stage is entirely carried

out as preprocessing. As a result, a set of distance

labels is obtained, encoding the proximity of every

mesh element to the contour for a ﬁxed point of view.

Since this analysis will be carried out for a set of NC

points of view, the ﬁnal result will be NC sets of la-

bels, being each set valid for the analyzed point of

view. Subsections 3.1.1–3.1.4 give a detailed expla-

nation of this process.

3.1.1 Mesh Mapping

Given a visualization plane, the 3D mesh is projected

on it by applying the proper projection matrix to the

coordinates of each vertex. In order to extract the ob-

ject’s silhouette, it is necessary to create a binary im-

age where distance measurements can be made. For

that purpose the visualization plane is partitioned into

cells forming a grid which can be seen as a 2D digi-

tal image. The number of cells making up the grid is

analogous to the image resolution; consequently the

parameterization of this value allows the analysis at

different resolutions.

Every face belonging to the projected polygonal

mesh is tested to ﬁnd the cells of the 2D grid with

which it intersects.

A data structure is updated where every grid ele-

ment keeps track of the faces intersecting with it. This

way, the posterior backprojection of distance values

is straightforward. This procedure is computationally

expensive, but affordable as pre-processing.

3.1.2 Binary Image Computation

In the case that only the external contour has to be pre-

served, the binary image is extracted from the grid oc-

cupancy information, setting as object every cell with

any face mapping over it. Object pixels adjacent to the

background will determine the external silhouette.

However, since internal silhouettes are known to

have a big impact in the visual quality perceived by

a human observer, their preservation is also desirable.

Detection of internal contours cannot be directly per-

formed in image space, but it can be easily carried

out in object space. By checking the angle formed

between a face normal and the visual vector it can

be concluded whether it is a frontfacing or backfac-

ing face. All the vertices shared by backfacing and

frontfacing facets are tagged as silhouette. With this

information, the occupancy binary image is modiﬁed

in the following way: an object pixel is set as back-

ground if a face containing a silhouette vertex projects

onto it. With this modiﬁcation, the silhouette (internal

and external) will be determined by the background

pixels which are adjacent to an object pixel. Figure 2

illustrates the extraction of both internal and external

contours.

3.1.3 Distance Transform Computation

Once the 2D image is obtained, the next stage consists

in obtaining a distance image by applying a distance

transform to the binary image. The result is a new

image where the assigned intensity values increase as

the pixel gets further away from the background.

MESH SIMPLIFICATION USING DISTANCE LABELS FOR VIEW-INDEPENDENT SILHOUETTE

PRESERVATION

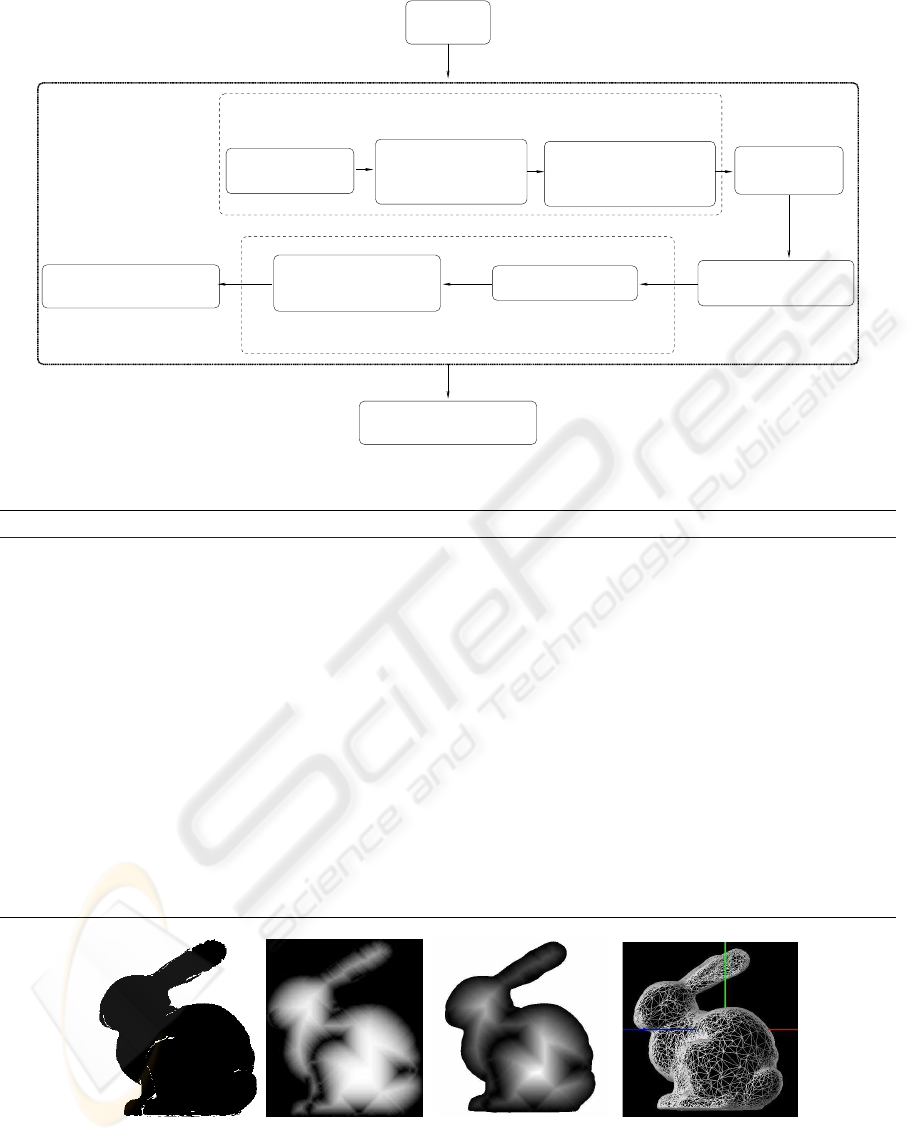
Original

3D mesh

3D Mesh simplification

Set of distance labels

for the processed view

Binary image

computation

2D View

selection

3D Mesh projection

over the selected

view plane

the mesh projection

configurable grid over

Overlapping of the 2D

Label backprojection

over original 3D mesh

Distance Transform

computation

For each point of view

Mesh labelling

Mesh mapping

2D Grid labelling

Figure 1: Mesh simpliﬁcation stages.

Algorithm 1 Pseudo-code of the pre-processing stage.

1: {INPUTS: 3D mesh, visualization parameters}

2: {OUTPUT: Collection of view-dependent labels}

3: Create a 2D grid over the visualization plane of the 3D input mesh

4: for all precomputed point of view do

5: for all grid-cells do {It is computed in a pre-processing stage}

6: Label each grid-cell with the 3D mesh vertices that project onto it

7: end for

8: Extract a binary image using the grid-cells occupation {Each pixel represents a grid cell}

9: Compute a Distance Transform over the binary image

10: Assign to each grid-cell the distance value of its associated pixel

11: for all grid-cells do {Assign labels to 3D vertices}

12: Backproject its distance value to all the 3D mesh vertices that project onto it and obtain a view-dependent

set of labels

13: end for

14: end for

15: Store distance labels together with the point of view parameters

(a) Internal and exter-

nal contours extracted

in 3D space.

(b) Distance Trans-

form.

projection.

(d) Simpliﬁcation

preserving the silhouette.

Figure 2: Extraction of both internal and external contours.

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

3.1.4 Mesh Labelling

At this point, the distance of an object pixel to the

background has already been computed. Previously,

the correspondences between pixels and the facets

mapping into them have also been calculated. There-

fore, the labelling of every face with a value repre-

senting its distance from the background is a simple

process. The distance label of a pixel, which is equiv-

alent to a grid cell, is assigned to all the faces that

intersect with the cell.

As a result a set of labels is obtained, where every

label belongs to a face and represents its proximity to

the contour for the analyzed point of view.

The same approach may be followed when the dis-

tance label is assigned to vertices or edges instead of

faces. Figure 3 shows the results of backprojecting

the distance values onto the mesh. Fig. 3(a) and 3(d)

show a rendered view of the original mesh. Fig. 3(c)-

(b) and 3(e)-(f) represent the same meshes under dif-

ferent points of view. The grey levels in the images

represent distance to the silhouette (lighter intensities

represent higher distances to the contour).

3.2 Distance Labels Interpolation for

New Points of View

Whenever the point of view from which the model is

to be rendered does not belong to the preprocessed set

of views, there is no valid set of distance-labels pre-

computed. In this case, the approach followed in this

work interpolates a new set of distance-labels from

the precomputed ones.

Two approaches have been implemented: the ﬁrst

one consists in using the labels from the closest pre-

computed view; the second one interpolates for every

vertex v

the labels of the same v

in the n closest

views in the following way: Let PV ={PV

,..PV

}

be the set of precomputed points of view; {PV

.labels}

the set of labels precomputed for the point of view

; PV

.labels

the label of the vertex v

for the

point of view PV

; and ﬁnally, PV

the current

point of view, for which a set of labels is needed.

Then,

if PV

∈ PV then

.labels are valid labels

else

Let {PV

..PV

} be the subset of n closest pre-

computed points of view

for j = 1 to nv do {nv is the number of vertices

of the mesh}

.labels

∑

k=1

(PV

.labels

)/n

end for

end if

This way a new set of distance-labels is obtained.

Since this estimation is performed in real time, com-

putational efﬁciency is highly desired. For this rea-

son, the precomputed set of views are regularly dis-

tributed, allowing the detection of the closest views to

take a constant time.

At this point, a tagged mesh can be obtained for

any point of view, using either precomputed distance-

labels or estimated ones.

3.3 Mesh Simpliﬁcation

The method’s last stage is also the ﬁnal goal of the

whole process, where the extracted distance values

are used for mesh simpliﬁcation purposes.

The use of the distance labels depends on the

selected simpliﬁcation technique. The work pre-

sented here has been based on the Jade approach,

a vertex decimation technique based on global er-

ror (Ciampalini et al., 1997). The distance infor-

mation is computed for the vertices of the original

mesh. Since the vertices belonging to a simpliﬁed

model are a subset of the original mesh, the precom-

puted distance labels are valid for any level of detail.

Multi-Tessellations obtained through the application

of the Jade method are freely distributed with the MT-

Package.

The proximity of every facet to the contour is

taken into account in the extraction stage. This means

that for a given error threshold, the error allowed in

regions close to the silhouette is reduced according to

a predeﬁned law.

The implemented solution, requires the deﬁnition

of two parameters:

• Distance interval: range of distance labels which

identify the region where a more accurate approx-

imation is desired.

• Error factor f : the purpose of this parameter is to

deﬁne a lower error threshold for the portion of

the mesh within the region of interest.

The width of the contour area can be simply mod-

iﬁed by changing the range of distance labels that

deﬁne the region of interest. In our case, the range

is deﬁned by setting a threshold over the minimum

distance of the vertices belonging to a face. Given

a distance threshold, and a vertex v

of triangle t

(∀t

∈ 3D mesh):

if PV

.labels

≤ distance threshold then

∈ contour

else

6∈ contour

end if

MESH SIMPLIFICATION USING DISTANCE LABELS FOR VIEW-INDEPENDENT SILHOUETTE

PRESERVATION

(a) Original Bunny

mesh.

(b) Distance com-

puted for the orien-

tation shown in Fig.

(a).

puted for mesh in

Figure (a) under ro-

tation .

(d) Original shell

mesh.

(e) Distance com-

puted for the orien-

tation shown in Fig.

(d).

(f) Distance com-

puted for mesh in

Figure (d) under ro-

tation.

Figure 3: Backprojection of distance values over the 3D model. Mesh vertices color represent the backprojected distance

label with grey levels proportional to the distances to the external silhouette.

Remember that PV

is the current point of view and

.labels have been extracted following the algo-

rithm described in section 3.2.

The error factor allows to reﬁne the quality of

the approximation in the contour region taking into

account the threshold error ﬁxed for the rest of the

model. Given a global allowed error e we can deﬁne

a more restrictive error that will be tolerated in the

contour region. Given the restriction factor f < 1, the

allowed error e

will be computed in the following

manner:

if t

6∈ contour then

= e

else

= e · f

end if

If the allowed error is uniform along the model, then

) = e ∀t

∈ 3D mesh

Again, other error functions are also feasible.

4 RESULTS

The experimental results presented in this section

were obtained by applying the technique previously

described to Multi-Tesselations either distributed to-

gether with the MT-Package or generated from avail-

able surface models. The precomputed collection of

distance-labels has been obtained from a regular dis-

tribution of orthographic cameras over a bounding

sphere sampled every 15 degrees. The results pre-

sented in ﬁgure 4 show simpliﬁed models obtained

by imposing a restrictive error threshold over the sil-

houette, setting the error factor to 0. This means that

no error is allowed on the region of interest. It can be

seen that the rest of the mesh is coarser (it has suffered

a strong simpliﬁcation process), while the density of

triangles over the silhouette is extremely high. Polyg-

onal meshes rendered in blue correspond to precom-

puted points of view, while meshes rendered in red

color are interpolated ones.

Figures 4 and 5 show the transition between two

precomputed points of view, making use of the closest

precomputed camera, while ﬁgure 6 shows the same

transition interpolating between the four closest pre-

computed cameras. It can be noticed in the video ac-

companying the paper that transitions are smoother

when using interpolated distance-labels. However,

the fact that the thickness of the contour can be pa-

rameterized, allows to work with wider silhouettes,

decreasing this way the perceived changes between

consecutive views. This effect can be better appre-

ciated in ﬁgures 4 and 5 that show the simpliﬁcation

of the mesh obtained by imposing a restrictive error

threshold over the silhouette and varying the distance

interval. In both cases, the error factor was set to 0,

meaning that no error is allowed on the external con-

tour. Using greater error factors would result in sil-

houettes with greater approximation errors as it can

be noticed in Fig. 7(a) and 7(b). The region of interest

(the mesh portion considered to be near the silhouette)

is made up of faces whose vertices have a minimum

distance label less than or equal to 2 (Fig. 4) and less

than or equal to 4 (Fig. 5). It can be seen that the rest

of the mesh is coarser (it has suffered a strong simpli-

ﬁcation process), while the density of triangles over

the silhouette is extremely high.

In addition to a visual inspection, an objective

measurement of the approximation error has also been

performed. The difference between the two polygonal

meshes to be compared is computed following an ap-

proach similar to (Aspert et al., 2002): given a mesh

M1 and a coarser approximation M2, for every vertex

of M1 the minimum distance to the faces belonging

to M2 is computed. A visual representation of the

deviation is shown by coloring M1 with a predeﬁned

color palette. Figure 7(c) presents the results of mea-

suring the difference between the original model and

the simpliﬁcation extracted in ﬁgure 7(a). Figure 7(b)

measures the difference between the original model

and a homogeneous LOD extracted over the whole

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

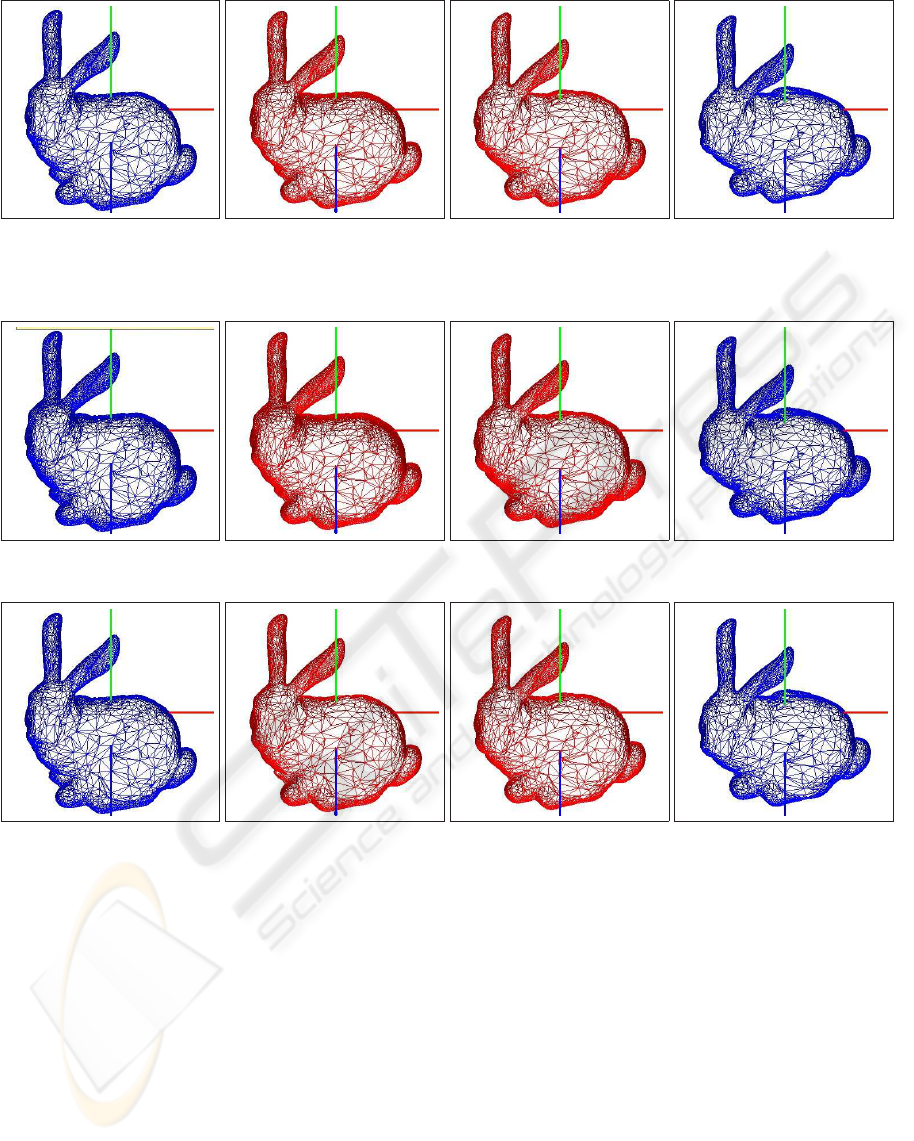
Figure 4: Transition between precomputed points of view (in blue) showing the extracted silhouettes for new points of view

(in red) using the closest view. Bunny with a rotation over the X axis of θ = 45

, θ = 50

, θ = 55

and θ = 60

setting

distance interval=2.

Figure 5: Same experiment of Fig. 4 setting distance interval=4.

Figure 6: Same transition of Fig. 4 interpolating from the 4 closest views.

model using the same global error allowed in 7(c).

From the error distribution it can be concluded that

the approximation in the silhouette is quantitatively

better with our method. Regarding computational is-

sues, cost in terms of memory requirements is of one

extra value per vertex and per precomputed camera.

By delimiting the sector where the observer next po-

sition will fall into, the number of cameras in memory

may be noticeably decreased. With respect to com-

putational cost, it has to be noted that all the heavy

computation is performed at pre-processing time. The

most expensive step is the mesh mapping over the 2D

grid, in order to collect the information needed for

backprojecting the distance values. Efﬁcient imple-

mentations for these operations using spatial data par-

titioning could be considered.

Execution time measures have been acquired in

order to compute the overload of managing distance-

labels with respect to extracting a simpliﬁcation from

a Multi-Tessellation without distance-labels. In both

cases, the parameters have been set in such a way

that the extracted meshes are at full-resolution, pro-

ducing this way the same load for the rendering stage.

With this experiment, measured times do not take into

account the advantage of multiresolution modelling,

that would result in the rendering a model with less

number of triangles. Table 1 shows the total time

spent in extracting a LOD from a distance-labelled

mesh versus the total time required for extracting an

homogeneous mesh of the same number of faces. Ta-

MESH SIMPLIFICATION USING DISTANCE LABELS FOR VIEW-INDEPENDENT SILHOUETTE

PRESERVATION

(a) Simpliﬁed model with

f = 0 and distance interval=4.

(b) Simpliﬁed model with

f = 0.2 · e and distance inter-

val=4.

compared to the original

mesh.

(d) Approx. error for a LOD

using the same global error as

in 7(a) .

Min. value=0 Max. value=1.273

(e) Color palette used for representing ap-

proximation errors.

Figure 7: Simpliﬁed models modifying the error factor. Visual representation of approximation error rendered under rotation

for a better perception of values.

Table 1: Statistics data extracted from executions using the closest precomputed point of view.

Model # facets TT (ms) PLI % PES % PRS % TTH (ms) OAH %

Shell 46550 45,65 0,04 23,85 76,10 43,84 3,96

Bunny 69451 69,22 0,02 24,65 75,32 66,91 3,33

Mannequin 204957 208,65 0,01 19,49 80,50 204,74 1,87

Sphere 360612 430,11 0,00 22,77 77,23 418,88 2,61

Table 2: Statistics data extracted from executions interpolating between the 4 closest points of view.

Model # facets TT (ms) PLI % PES % PRS % TTH (ms) OAH %

Shell 46550 55,17 17,10 20,02 62,88 44,22 19,84

Bunny 69451 82,39 16,24 20,97 62,79 66,93 18,76

Mannequin 204957 279,51 16,87 16,64 66,49 227,96 18,44

Sphere 360612 465,15 16,03 18,70 65,27 374,94 19,39

ble 1 also shows the percentage of the total time spent

in obtaining the closest view’s labels, extracting a

level of detail from the multi-tessellation, and render-

ing the ﬁnal model. It can be observed that a very

small part of the total time is spent in getting distance-

labels for the current view. Table 2 shows the same

execution times as Table 1 measured interpolating be-

tween the 4 closest cameras.

It can be observed that using the closest camera

results in a lower overload (OAH < 4 %), since the

estimation of labels for new points of view is com-

putationally lighter. An additional advantage is the

fact that the extra time required for ﬁnding the closest

point of view is constant, independently of the size of

the mesh.

The notation used in Tables 1 and 2 is the follow-

ing:

TT: Total execution time (ms).

TTH: Idem considering an homogeneous LOD.

PLI: % of total execution time involved in accessing

the valid or interpolated distance-labels.

PES: Idem involved in the extraction of a LOD from

the multi-tessellation.

PRS: Idem involved in the rendering of the extracted

mesh.

OAH: Overhead introduced by using the proposed

method versus obtaining an homogeneous LOD

from the multi-tessellation.

The computer used in the tests was a 3.2 GHz Pen-

tium IV CPU with 1 GB of main memory and a

general purpose graphics card (NVIDIA GEFORCE

7800 GTX).

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

5 CONCLUSIONS AND FUTURE

WORK

Simpliﬁcation algorithms are usually guided by some

criteria in order to select which elements of the mesh

shall be removed or replaced. Introducing precom-

puted distance labels as part of the guiding metrics is

a straightforward process, opening a new way to de-

sign a set of techniques which are useful for includ-

ing a wide range of criteria in mesh simpliﬁcation al-

gorithms. Additionally, the approach presented here

can be applied in order to achieve higher resolution in

other relevant regions besides the silhouette, such as

visually outstanding areas, or semantically important

parts.

The results presented here suggest that the use

of distance information is a promising approach for

mesh simpliﬁcation techniques, since adding distance

labels to mesh elements provides more information

than the conventional methods based on the extrac-

tion of the silhouette edges. This fact becomes patent

in the examples shown, where it can be seen that

by increasing the width of the preserved contour, the

quality of the silhouette in interpolated views also in-

creases. This ﬂexibility in parameterization of con-

tour’s width, makes also possible to use the closest

view instead of interpolating between the n-closest

views, resulting in a valuable saving of computational

time.

The proposed technique may be easily adapted to

a wide range of simpliﬁcation methods, since distance

information can be assigned to any element of the

mesh (vertices, edges or faces). This fact implies that

the nature of the basic underlying operator (vertex re-

moval, edge collapse, etc) does not impose additional

limitations. Furthermore, the applicability of distance

labels goes from off-line simpliﬁcation processing to

run-time selective reﬁnement.

Simpliﬁcation techniques have a wide range of ap-

plications in leisure, science, industry, arts, etc. All of

them can beneﬁt from the improvements in the quality

of the simpliﬁed models.

The work presented here may be extended in the

following ways:

• Integrating distance to the silhouette into other

mesh simpliﬁcation methods besides the multi-

tessellation.

• Applying different error factors to internal and ex-

ternal contours.

• Estimating changes in the position of the point of

view, allowing the computation of distance-labels

in advance.

• Performing an analysis of variability between

points of view, in order to optimally redistribute

the precomputed cameras.

ACKNOWLEDGEMENTS

This work has been partially funded by the the

Spanish Ministry of Education and Science (grant

TIN2007-67188) and Government of the Community

of Madrid (grant S-0505/DPI/0235; GATARVISA).

The authors also thank to the Geometric Mod-

elling and Computer Graphics Research Group for

distributing the MT-Package.

REFERENCES

Aspert, N., Santa-Cruz, D., and Ebrahimi, T. (2002). Mesh:

Measuring error between surfaces using the hausdorff

distance. In Proceedings of the IEEE International

Conference in Multimedia and Expo (ICME), vol-

ume 1, pages 705–708. ISBN 0-7803-7304-9.

Borgefors, G. (1984). Distance transformation in arbitrary

dimensions. Computer Vision, Graphics and Image

Processing, 27:321–345.

Cheng, I. and Boulanger, P. (2005). A 3D perceptual met-

ric using just-noticeable-difference. In Proceedings

of Eurographics 2005, pages 97–100. Eurographics.

ISSN 1017-4656.

Ciampalini, A., Cignoni, P., Montani, C., and Scopigno, R.

(1997). Multiresolution decimation based on global

error. The Visual Computer, 13(5):228–246. ISSN

1432-2315.

Clark, J. H. (1976). Hierarchical geometric models for visi-

ble surface algorithms. Communications of the ACM,

19(10):547–554. ISSN 0001-0782.

Cohen, J., Olano, M., and Manocha, D. (1998).

Appearance-preserving simpliﬁcation. In Proceedings

of SIGGRAPH’98, Annual Conference Series, pages

115–122. ISBN 0-89791-999-8.

De Floriani, L., Kobbelt, L., and Puppo, E. (2005). A sur-

vey on data structures for level-of-detail models. In

Dodgson, N. A., Floater, M. S., and Sabin, M. A., edi-

tors, Advances in Multiresolution for Geometric Mod-

elling, Series in Mathematics and Visualization, pages

49–74. Springer Verlag, Berlin. ISBN 3-540-21462-3.

De Floriani, L., Magillo, P., and Puppo, E. (1997). Building

and traversing a surface at variable resolution. In Pro-

ceedings of IEEE Visualization 97, pages 103–110.

IEEE Computer Society Press. ISBN 0-8186-8262-0.

De Floriani, L., Magillo, P., and Puppo, E. (1998). Efﬁcient

implementation of multi-triangulations. In Proceed-

ings of IEEE Visualization VIS’98, pages 43–50. IEE

Copmuter Society Press. ISBN 0-8186-9176-X.

MESH SIMPLIFICATION USING DISTANCE LABELS FOR VIEW-INDEPENDENT SILHOUETTE

PRESERVATION

Garland, M. (1999). Multiresolution modeling: Survey and

future opportunities. In STAR Proccedings of Euro-

graphics’99, volume 1 of Eurographics technical re-

port series, Geneva, Switzerland. Eurographics Asso-

ciation.

Garland, M. and Heckbert, P. (1998). Simplifying sur-

faces with color and texture using quadric error met-

rics. In Proceedings of IEEE Visualization VIS’98,

pages 263–270. IEEE Computer Society. ISBN 0-

8186-9176-X.

Geometric Modeling and Computer Graphics Research

Group (2005). The MT (Multi-Tessellation) Pack-

age. Web. Retrieved march 27, 2007, from source,

http://gmcg.disi.unige.it/.

Hoppe, H. (1997). View-dependent reﬁnement of progres-

sive meshes. In Proceedings of the ACM Conference

SIGGRAPH’97, Computer Graphics Annual Confer-

ence Series, pages 189–198, New York. ACM. ISBN

0-89791-921-1.

Jones, M. W., Bærentzen, A., and

amek, M. (2006). Dis-

crete 3D distance ﬁelds: A survey of techniques and

applications. IEEE Transactions on Visualization and

Computer Graphics, 12(4):581–599.

Lindstrom, P. and Turk, G. (2000). Image-driven simpliﬁca-

tion. ACM Transactions on Graphics (ToG), 19:204–

241. ISSN 0730-0301.

Luebke, D. and Erikson, C. (1997). View-dependent sim-

pliﬁcation of arbitrary polygonal enviroments. In

Proceedings of 24

annual conference on Computer

graphics and interactive techniques, SIGGRAPH,

pages 199–208, New York. ACM. ISSN 0-89791-896-

Luebke, D., Reddy, M., Cohen, J. D., Varshney, A., Watson,

B., and Huebner, R. (2003). Level of Detail for 3D

Graphics. The Morgan Kaufmann series in computer

graphics and geometric modeling. Morgan Kauffmann

Publishers, San Francisco. ISBN 1-55860-838-9.

Luebke, D. P. (1998). View-dependent simpliﬁcation of ar-

bitrary polygonal environments. Ph. D. dissertation,

University of North Carolina.

Luebke, D. P. (2001). A developer’s survey of polygonal

simpliﬁcation algorithms. IEEE Computer Graphics

and Applications, 21(3):24–35. ISSN 0272-1716.

Nystr

om, I. (1997). On Quantitative Shape Analysis of Dig-

ital Volume Images. Ph. D. dissertation, Uppsala Uni-

versity.

O’Sullivan, C., Howlett, S., Morvan, Y., McDonnell, R.,

and O’Conor, K. (2004). Perceptually adaptive graph-

ics. In Schlick, C. and Purgathofer, W., editors, Eu-

rographics State-of-the-Art Report (EG-STAR), vol-

ume 6, pages 141–164. Eurographics Association, Eu-

rographics Association.

Puppo, E. and Scopigno, R. (1997). Simpliﬁcation, LOD

and multiresolution principles and applications. In

Fellner, D. and Szirmay-Kalos, L., editors, EURO-

GRAPHICS’97, volume 16. Tutorial Notes PS97 TN4.

Raskar, R. and Cohen, M. F. (1999). Image precision silhou-

ette edges. In Proceedings of the Symposium on Inter-

active 3D Graphics, pages 135–140. ISBN 1-58113-

082-1.

Reddy, M. (1997). Perceptually Modulated Level of Detail

for Virtual Environments. Ph. D. dissertation, Univer-

sity of Edinburgh.

Rosenfeld, A. and Pfaltz, J. (1966). Sequential operations

in digital picture processing. Journal of the Associa-

tion for Computing Machinery, 13(4):471–491. ISSN

0004-5411.

Rosenfeld, A. and Pfaltz, J. (1968). Distance functions on

digital pictures. Pattern Recognition, 1:33–61.

Sander, P. V., Gu, X., Gortler, S. J., Hoppe, H., and Sny-

der, J. (2000). Silhouette clipping. In Proceedings of

the 27th annual conference on Computer graphics and

interactive techniques SIGGRAPH 2000, pages 327–

334. ISBN 1-58113-208-5.

Sintorn, I.-M. (2005). Segmentation Methods and Shape

Descriptions in Digital Images. Ph. D. dissertation,

Swedish University of Agricultural Sciences.

Sud, A., Govindaraju, N., Gayle, R., and Manocha, D.

(2006). Interactive 3d distance ﬁeld computation us-

ing linear factorization. In Proceedings of the Sympo-

sium on Interactive 3D Graphics and Games, pages

117–124, New York, NY, EEUU. ACM Press. ISBN

1-59593-295-X.

Svensson, S. (2001). Representing and Analyzing 3D Digi-

tal Shape Using Distance Information. Ph. D. disser-

tation, Swedish University of Agricultural Sciences.

Teschner, M., Kimmerle, S., Zachmann, G., Heidelberger,

B., Raghupathi, L., Fuhrmann, A., Cani, M.-P., Faure,

F., Magnenat-Thalmann, N., and Strasser, W. (2004).

Collision detection for deformable objects. In Eu-

rographics State-of-the-Art Report (EG-STAR), pages

119–139. Eurographics Association, Eurographics

Association.

Williams, N., Luebke, D., Cohen, J. D., Kelley, M., and

Schubert, B. (2003). Perceptually guided simpliﬁca-

tion of lit, textured meshes. In Proceedings of the Sym-

posium on Interactive 3D Graphics, Session 5: simpli-

ﬁcation and meshes, pages 113–121, New York. ACM

Press. ISBN 1-58113-645-5.

Xia, J. C. and Varshney, A. (1996). Dynamic view-

dependent simpliﬁcation for polygonal models. In

Yagel, R. and Nielson, G. M., editors, IEEE Visual-

ization ’96, pages 335–344. ISBN 0-89791-864-9.

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications