
VISUALIZING MULTIPLE SCALAR FIELDS ON A SURFACE
Mohammed Mostefa Mesmoudi
Institut Universitaire de Formation des Maˆıtres de Cr´eteil, 12 rue George Enesco, 94046 Cr´eteil, France
Leila De Floriani, Paola Magillo
Department of Computer Science and Information Science, University of Genova, Via Dodecaneso, 35 -16146 Genova, Italy
Keywords:
3D Visualization, geometric modeling, multivariate scalar fields, offsetting.
Abstract:
We present a new technique for the simultaneous visualization of an arbitrary number of scalar fields defined
on a surface. The technique is called Generalized Atmosphere Upper Bound Level (GAUBL), since it is an
evolution of our previous AUBL technique, that allowed for the visualization of a single scalar field. The
generalized AUBL can highlight the dependencies and interactions between many scalar fields, and can handle
a multi-valued scalar field as a special case. We have implemented the GAUBL into a visualization tool that
handles triangle-based surface models, and we show here some experimental results.
1 INTRODUCTION
In many applicationsof computergraphics (e.g., med-
ical imagery, visual data mining) the visualizationof a
scalar field representing some data relative to a three-
dimensional shape is a basic tool to explore and un-
derstand the behaviorof the field. Several scalar fields
may be interesting to be studied simultaneously, to
highlight their dependencies and their mutual influ-
ence. For example, in medical imagery, oxygen rate
and sugar rate can be visualized together to study the
brain surface activity. Unfortunately, human percep-
tion is limited to three dimensions and the visualiza-
tion of those scalar fields needs additional indepen-
dent directions to be achieved. To avoid this obstacle,
we need to find a natural way to embed these multi-
dimensional data in the Euclidean space R
3
so that
the result still has some meaningful interpretation, es-
pecially for comparison purposes. Here, we propose
a visualization technique that allows this embedding
and thus gives us the opportunity to explore and study
multi-valued scalar fields defined on the same sur-
face. The basic idea is to convert the scalar fields into
a sequence of vector fields on the surface and then
display a surface for each vector field according to
some constraints. We call the new visualization tech-
nique Generalized AUBL (GAUBL), since it general-
izes to multi-dimensional scalar fields the AUBL (At-
mosphere Upper Bound Level) technique introduced
in (Mesmoudi et al., 2007). This latter allows the
3D visualization of just one scalar field defined over a
surface embedded in the three-dimensional Euclidean
space. The generalized AUBL technique is easily
adapted to handle discrete scalar fields defined over
triangulated surfaces. We present here an interactive
visualization tool that implements the GAUBL tech-
nique for triangle meshes. We use such tool to il-
lustrate the results of the GAUBL visualization tech-
nique. The remainder of the paper is organized as
follows. In Section 2, we review related work. In
Sections 3, we briefly review the AUBL visualization
technique. In Section4, we introduce the GAUBL vi-
sualization technique that generalizes AUBL to visu-
alizing several scalar fields. In Section 5, we present
the visualization tool implementing the GAUBL tech-
nique for discrete scalar fields defined on triangulated
surfaces, and some results. In the last Section, we
draw some concluding remarks.
2 RELATED WORK
To represent multi-dimensional data in the three di-
mensional space, we need to reduce their dimension-
ality without loosing important information. Geo-
138
Mostefa Mesmoudi M., De Floriani L. and Magillo P. (2008).
VISUALIZING MULTIPLE SCALAR FIELDS ON A SURFACE.
In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 138-142
DOI: 10.5220/0001097201380142
Copyright
c
SciTePress

metric projection techniques allow meaningful visu-
alization of multi-dimensional data. Some of them
are statistically based techniques (Huber, 1985). Par-
allel coordinates techniques (Inselberg, 1985) repre-
sent attributes as parallel lines in the two-dimensional
space. Hierarchical techniques use a partitioning of
the space into subspaces. In stacking techniques, the
space is partitioned into 2D subspaces that are stacked
in a recursive way (Blanc et al., 1990). The worlds-
within-worlds technique partitions the 3D space into
nested subspaces: three attributes are selected and vi-
sualized through a 3D surface, then, for any point on
the surface selected by the user, three other attributes
are visualized in the same manner (Feiner and Besh-
ers, 1990). When some attributes are functions of two
or three dependent parameters (like in terrain model-
ing, image processing, medical imagery), the graph-
ical representation of these attributes has more sense
if it can be represented in the ambient space by a sur-
face. The AUBL technique developed in (Mesmoudi
et al., 2007) allows the 3D visualization of a scalar
field defined over a surface embedded in the 3D Eu-
clidean space. This technique when applied to a con-
stant function is known as offsetting (Rossignac and
Requicha, 1985; Frisken et al., 2000; Cohen et al.,
1996). In (Taylor, 2002; Kirby et al., 1999; Craw-
fis and Allison, 1991), techniques to represent multi-
ple scalar fields (at most four fields) on the same sur-
face have been proposed. These techniques combine
colors, contour lines, spot noise texture generation,
reaction-diffusion texture generation, surface albedo,
data-driven spots and oriented slivers.
3 THE AUBL VISUALIZATION
TECHNIQUE
Two-dimensional manifolds (without boundary) are
(smooth) surfaces that are locally diffeomorphic to
discs in R
2
. At each point p of a surface S, the tangent
plane T
p
S is defined and a unit normal vector
−→
n
p
to S
at point p can be drawn. This latter correspondence is
called the Gauss map. Vector
−→
n
p
with an orthonormal
basis of T
p
S generates a mobile orthonormal frame of
the Euclidean three-dimensional space R
3
whose ori-
gin is located at point p (see Figure 1(a)). The key
idea of the AUBL visualization technique comes from
the graphical representation of 2D scalar fields. The
graphical representation of a scalar field g on a two-
dimensional domain D
∼
=
D×0 is a surface embedded
in R
3
such that the height of each point on the surface
corresponds to the value of g at this point and if the
frame is orthonormal then the distance of the point to
the Oxy-plane is equal to the absolute value of g at
D
g(D)
x
y
O
m
z
g(m)
(a) (b)
Figure 1: (a) A surface with its tangent plane and normal
vectorial space at a point. (b) Graphical representation of a
function g over a domain D ⊂ R
2
.
this point (see Figure 1(b)). By generalizing this idea,
we can give a graphical representation of 3D scalar
fields.
Definition 1 Let
−→
n
p
be the unit normal vector of S at
point p. The graphical representation of the scalar
field f over S is the surface S ⊂ R
3
defined by the
vector field
˜
f(p) := p+ f(p)
−→
n
p
, i.e.,
S = {p + f(p)
−→
n
p
: p ∈ S} (1)
Note that vector
−−−→
p
˜
f(p) is normal to S at p and
k
−−−→
p
˜
f(p) k=| f(p) |.
The graphical representation of function f defines an
atmosphere layer over surface S. The thickness of
the layer is given by the function values. In (Mes-
moudi et al., 2007), we have defined graphical opera-
tions which can be used to better analyze the shape of
the surface and thus the properties of the field. Scal-
ing multiplies the field vector value through a factor;
inflation and deflation translate
˜
f(p) in direction of
the normal vector
−→
N
p
by a constant positive and nega-
tive value, respectively. Details can be found in (Mes-
moudi et al., 2007).
Definition 2 Under such assumptions, we call the
graphical representation S of f, the atmosphere up-
per bound layer (AUBL) of the pair (S, f).
In Figure 2, we illustrate the above situation for the
unit sphere x
2
+ y
2
+ z
2
= 1 with an atmosphere cor-
responding to the function f(x, y, z) = x
2
− y
2
− 1.
4 THE GENERALIZED AUBL
TECHNIQUE
The main idea in generalizing the AUBL visualization
technique comes from the fact that the AUBL tech-
nique gives a vector field
−−−→
p
˜
f(p)
p∈S
over surface S.
VISUALIZING MULTIPLE SCALAR FIELDS ON A SURFACE
139

(a) (b)
Figure 2: (a) A cross section of the unit sphere with an at-
mosphere defined by function f(x, y, z) = x
2
− y
2
− 1. (b)
Visualization of S corresponding to
˜
f.
We use this idea to generate a vector field over S for
any number of functions defined on S. We will show
that successive vector fields can be defined depending
on the number of functions. Assume that two scalar
fields f and g are defined simultaneously on S. AUBL
visualization technique is used to visualize function f
as surface S . To visualize function g with f, a col-
oring map c is defined on the image Im(g). Then a
vector function ˜g can be defined as follows: for each
point p ∈ S we associate the pair (
˜
f(p), c(g(p))). Fi-
nally, functions (f, g) are visualized as a colored sur-
face, that we denote C S to distinguish it from S . Fig-
ure 3(a) gives an example of two functions f and g
defined on the unit sphere S
2
. Let now f, g and h be
D
y
x
z
m
S
(f(m), g(m), h(m))
(a) (b)
Figure 3: (a) Visualization of two functions f (x, y, z) =
x
2
+y
2
and g(x, y, z) = z
2
defined over the unit sphere. Func-
tion f is represented as a surface containing the unit sphere
in its interior, and g is represented by a coloring map where
white and magenta correspond to low and high field values,
respectively. (b) Graphical representation of three scalar
fields over a surface S in R
3
.
three scalar fields defined on surface S. For each point
p ∈ S, we define a vector
−→
V
p
= ( f(p), g(p), h(p)).
This gives a vector field
−→
V
p
p∈S
over S (see Figure
3(b)). We define surface S := {p +
−→
V
p
: p ∈ S} as
the graphical representation of scalar fields f, g and
h over S. The direction and the intensity of each vec-
tor is influenced by the values of the three functions
f, g and h. Thus, interactions among these func-
tions can be seen (see Figure 4). For four scalar
Figure 4: Visualization of three functions f(x, y, z) = x
2
+
y
2
, g(x, y, z) = z
2
and h(x, y, z) = y− z defined over the unit
sphere, from two different points of view. Functions f , g, h
are presented as the surface of a vector field ( f, g, h).
fields f, g, h and k, we embed surface S in R
4
by
S ≈ S
′
:= {(x, y, z, 0) : (x, y, z) ∈ S}. For each point
p ∈ S we define a vector
−→
V
′
p
= ( f(p), g(p), h(p), k(p)).
Vectors
−→
V
′
p
p∈S
form a vector field over S
′
. Visual-
ization of scalar fields f, g, h and k can be achieved in
R
4
by constructing a new surface S
′
:= {(p, 0) +
−→
V
′
p
:
p ∈ S} = {(x
p
+ f(p), y
p
+ g(p), z
p
+ h(p), k(p))}.
Equivalently, S
′
can be seen as a surface S” := {(x
p
+
f(p), y
p
+ g(p), z
p
+ h(p)) : p ∈ S} in R
3
endowed
with a scalar field k. Function k can be seen as a color-
ing function of surface S”. Another way to represent
function k is to use the AUBL visualization technique
that permits to define a surface S ” ⊂ R
3
associated
with the pair (S”, k). We define thus (S”, S ”) to be the
graphical representation of scalar fields f, g, h and k.
Now, the generalization to five scalar fields can
be done as for the case of two scalar fields. We
represent the fourth scalar field by the AUBL tech-
nique as a surface S ” and the fifth scalar field by
a coloring function over surface S ”. The colored
surface C S ” with S” give a graphical representation
of the all five scalar fields (see Figure 5). For six
(a) (b)
Figure 5: Visualization of five functions f(x, y, z) = x
2
+y
2
,
g(x, y, z) = z
2
, h(x, y, z) = 2y− z + 3,k(p) = z and l(p) = x
defined over the unit sphere S
2
. (a) Surfaces S
2
, S” and S ”.
(b) The coloring function l is represented in C S ”.
scalar fields f, g, h, k, l and m, we shift surface
S to R
6
to get a surface S ≈ S
′
:= {(x, y, z, 0, 0, 0) :
(x, y, z) ∈ S}. Then for each point p ∈ S we de-
fine a vector
−→
V
′
p
= ( f(p), g(p), h(p), k(p), l(p), m(p)).
Vectors
−→
V
′
p
p∈S
form a vector field that traverses
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
140

over S
′
. Visualization of scalar fields f, g, h, k, l
and m can be achieved in R
6
by constructing surface
S
′
:= {(p, 0, 0, 0) +
−→
V
′
p
: p ∈ S} = {(x
p
+ f(p), y
p
+
g(p), z
p
+ h(p), k(p), l(p), m(p))}. Equivalently, S
′
can be seen as a surface S” := {(x
p
+ f(p), y
p
+
g(p), z
p
+ h(p)) : p ∈ S} embedded in R
3
with a vec-
tor field defined by vectors
−−→
V”
p
= (k(p), l(p), m(p)).
Then as for three scalar fields we can construct a sur-
face S ” defined by vectors
−−→
V”
p
. The visualization of
all scalar fields f, g, h, k, l and m is hence given
by two surfaces (S”, S ”) as in Figure 6. Following
(a) (b)
Figure 6: Visualization of six functions f (x, y, z) = x
2
+ y
2
,
g(x, y, z) = z
2
, h(x, y, z) = 2y − z + 3,k(p) = z, and m(p) =
−y
2
. Functions f, g and h form a first vector field S
′
over
S
2
. Then function k, l and m form a second vector field over
S
′
. (a) Surfaces S
′
and S ”. (b) Surfaces S
2
, S
′
and S ”.
the previous reasoning, we can extend (modulo 3) the
above visualization techniques to n scalar fields de-
fined over surface S. The AUBL technique, the color-
ing technique and thevector flowtechniqueforma ba-
sis of the visualization techniques that can be used to-
gether, or separately, following the rank of n (mod 3).
This extension gives a hierarchical representation of
scalar fields as described in the worlds-with-worlds
data mining representation technique (see Section 2
above).
5 EXPERIMENTAL RESULTS
Our GAUBL tool allows for the visualization of up to
four different scalar fields defined on a triangulated
surface. It is implemented in C with the OpenGL
graphical library and has a very simple user interface
developed with Glut. The surface is given as a tri-
angle mesh in indexed format (each vertex as three
coordinates, each triangle as three vertex indexes). A
scalar field can be provided in two forms: an explicit
list of field values at the mesh vertices (e.g., sampled
values of temperature, pressure etc.), or a mathemat-
ical formula to compute such values. Visualization
adapts to the current number of loaded scalar fields,
by selecting the appropriate GAUBL technique. Ad-
ditional inputs are represented by coloring functions
Figure 7: The sphere and four fields, with two different mul-
tiplication factors.
to map field values to color values specified in the
red-green-blue (RGB) format. The user can interac-
tively set parameters, as the translation factor for in-
flation / deflation, the multiplicative factor for scaling,
the coloring function, surface and background colors,
transparency effects, and, of course, he can rotate, pan
and zoom the entire scene. Figure 7 shows the unite
sphere along with the colored mesh representing four
scalar fields: f (p) = x, g(p) = y − z, h(p) = x
2
+ y
2
and k(p) = x, the last one rendered with a coloring
function going from red to blue through green. Figure
8 shows a mesh representing a girl and a field equal
to f(p) = z. In Figure 9 the same mesh is associ-
ated with a scalar field that simulates fattening of the
central part of the body, through a gaussian formula.
The figure shows the original surface and two fattened
versions, with different multiplication factors. Figure
10 shows a terrain with two scalar fields, where the
first one (giving the surface) is constant and the sec-
ond one (rendered as color scale) is g(p) = z. Infla-
tion and deflation correspond here to a version of the
same terrain after deposit of material (e.g. calcium
carbonate on the bottom of a lake in a cavern) or after
erosion, respectively.
Figure 8: Girl surface with one field f(p) = z.
VISUALIZING MULTIPLE SCALAR FIELDS ON A SURFACE
141
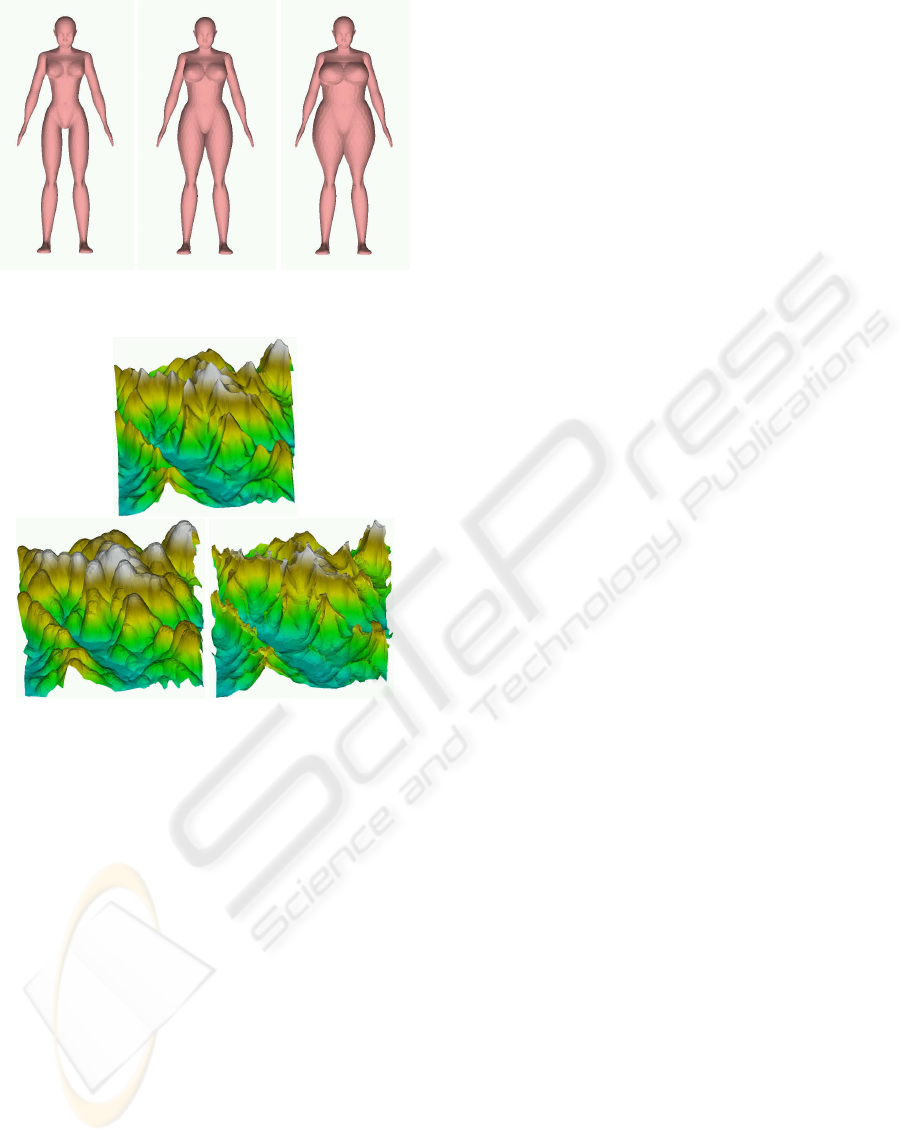
Figure 9: Girl surface with different multiplication factors.
Figure 10: A terrain and its inflated and deflated versions.
6 CONCLUDING REMARKS
We have presented the GAUBL visualization tech-
nique that allows displaying any number of scalar
fields defined on a surface, in the form of another
(possibly colored) surface embedded in 3D space. In
our ongoing work, we will improve our visualization
tool with new functionalities, such as showing alge-
braic information at a clicked point on the surface
(vector length, direction, position with respect to the
normal vector of the original surface,...). Moreover,
we plan to combine this visualization technique with
a mesh-based multi-resolution representation to allow
selective and adaptive offsetting of a surface.
ACKNOWLEDGEMENTS
This work has been partially supported by the Eu-
ropean Network of Excellence AIM@SHAPE un-
der contract number 506766, by the National Sci-
ence Foundation under grant CCF-0541032, by the
MIUR-FIRB project SHALOM under contract num-
ber RBIN04HWR8 and by the MIUR-PRIN project
on ”Multi-resolution modeling of scalar fields and
digital shapes”.
REFERENCES
Blanc, J. L., Ward, M., and Wittels, N. (1990). Exploring
n-dimensional databases. In Visualization’90, pages
230–238, San Fransisco, CA.
Cohen, L., Varshney, A., Manocha, D., Turk, G., Weber,
H., Agarwal, P., Brooks, P., and Wright, W. (1996).
Simplification envelopes. In Proc. ACM SIGGRAPH,
pages 119–128.
Crawfis, R. and Allison, M. (1991). A scientific visual-
ization synthetizer. In Proc. IEEE Viaualization’91,
IEEE CS Press, Los Alamitos, CA.
Feiner, S. and Beshers, C. (1990). World within world
: Metaphors for exploring n-dimensional virtual
worlds. In Proceedings UIST, pages 76–83.
Frisken, S. F., Perry, R. N., Rockwood, A. P., and Jones,
T. R. (2000). Adaptively sampled distance fields: A
general representation of shape for computer graphics.
Technical report, Mitsubishi Electric Research Labo-
ratories, Cambridge Research Center. TR2000-15.
Huber, P. J. (1985). Projection pusuit. Annals of Statistics,
13(2):435–474.
Inselberg, A. (1985). The plane with parallel coordinates.
Special Issue On Computational Geometry, The Vi-
sual Computer, 1:69–97.
Kirby, R., Marmanis, H., and Laidlaw, D. (1999). Visual-
izing multivalued data fron 2d incompressible flows
using concepts from painting. In Proc. IEEE Visual-
ization’99, IEEE CS Press, Los Alamitos, CA, pages
333–340.
Mesmoudi, M., Floriani, L. D., and Rosso, P. (2007). Theo-
retical foundations of 3d scalar fields visualization. In
Proceedings of Special Sesssions International con-
ference on computer vision theory and application,
pages 69–77, Barcelona Spain. INSTICC Press.
Rossignac, J. and Requicha, A. (1985). Offsetting oper-
ations in solid modeling. Computer Aided Design,
3(2):129–148.
Taylor, R. (2002). Visualizing multiple fields on the same
surface. Visualization Viewpoints, IEEE Computer
Graphics and applications, May/June:6–11.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
142
