A HIERARCHICAL SPATIAL INDEX FOR TRIANGULATED

SURFACES

Leila De Floriani, Marianna Facinoli, Paola Magillo and Debora Dimitri

Department of Computer and Information Science, University of Genova, Genova, Italy

Keywords:

Terrain models, Triangle meshes, Hierarchical spatial indexes.

Abstract:

We present the PM2-Triangle quadtree (PM2T-quadtree), a new hierarchical spatial index for triangle meshes

which has been designed for performing spatial queries on triangle-based terrain models. The PM2T-quadtree

is based on a recursive space decomposition into square blocks. Here, we propose a highly compact data

structure encoding a PM2T-quadtree, which decouples the spatial indexing structure from the combinatorial

description of the mesh. We compare the PM2T-quadtree against other spatial indexes by considering the

structure of the underlying domain subdivision, the storage costs of their data structures and the performance

in geometric queries.

1 INTRODUCTION

A terrain is a scalar ﬁeld z = f (x,y) deﬁned on a do-

main D. Function f is known only at a ﬁnite set

of data points. When the data points are irregularly

spaced in the x-y plane, the terrain is approximated

through a triangulated surface, called a Triangular Ir-

regular Network (TIN). A TIN consists of a decom-

position of the domain in the x-y plane as a triangle

mesh connecting the data points, and of a piecewise-

linear interpolant deﬁned on the triangles of the mesh.

The triangle mesh underlying a TIN is usually en-

coded in a topological data structure, such as, for in-

stance, the indexed data structure with adjacencies

(De Floriani and Hui, 2007). This is well suited for

navigation in the mesh through adjacencies, but it be-

comes quite inefﬁcient for spatial queries, such as

point location or window query, which involve focus-

ing on a portion of the domain. Since current mod-

els have a large number of triangles, of the order of

several millions, it is necessary to superimpose a spa-

tial index on the triangle mesh to expedite the search.

An approach for point location without a spatial index

ucke et al., 1999) is only possible for Delaunay tri-

angulations and convex domains.

There is a vast literature on both object-based or

space-based hierarchical spatial indexes, see (Samet,

2006) for a survey. Object-based indexes, such as

R-trees or their variants, are hierarchies of bounding

boxes (or sometimes spheres), and thus are not de-

signed for encoding connectivity of a set of entities,

like a polygonal map or a triangle mesh. The most

common space-based spatial indexes are quadtrees

and kD trees. Some of them have been deﬁned for

sets of points or for polygonal maps (e.g., the PM-

quadtrees), but the subdivision is based on the edges

of the map, and the topological structure of the map

is not encoded.

We propose here a new hierarchical spatial in-

dex based on triangles, that we call a PM2-Triangle

quadtree (or PM2T-quadtree for short), and we

present a compact data structure for it. Such data

structure separately encodes the combinatorial struc-

ture of the triangle mesh, which is the basis for mesh

navigation, and the structure of the spatial index, that

enhances the performances of spatial queries by re-

ducing the searching space.

The remainder of this paper is organized as fol-

lows. In Section 2 we present related works. In

Sections 3 we deﬁne the PM2T-quadtree and its data

structure. In Section 4 we show that the PM2T-

quadtree outperforms a number of alternative spatial

indexes. Finally, Section 5 contains some concluding

remarks.

2 RELATED WORK

In this Section, we brieﬂy review space-based hierar-

chical spatial indexes related to the new indexes pre-

sented here.

Quadtrees and kD-trees are spatial indexes for rep-

resenting a set of points. We describe here only a

De Floriani L., Facinoli M., Magillo P. and Dimitri D. (2008).

A HIERARCHICAL SPATIAL INDEX FOR TRIANGULATED SURFACES.

In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 86-91

DOI: 10.5220/0001097300860091

 SciTePress

quadtree for representing points in the plane, the PR-

quadtree (Orenstein, 1982). A PR-quadtree is gen-

erated by the recursive subdivision of the square do-

main, where the points are distributed, into nested

square blocks split through the middle point of the

block. The subdivision is described through a qua-

ternary tree, where every node is either a leaf, or an

internal node with four children corresponding to the

four sub-quadrants of its parent’s square. The shape

of a PR-quadtree is independent of the order in which

the points are inserted, since the subdivision is based

on the domain and the points are only in the leaves.

Several quadtrees have been proposed to store col-

lection of edges, see (Samet, 2006) for a detailed

treatment. The class of PM-quadtrees extend the PR-

quadtree to represent polygonal maps, by using sub-

division rules based on vertices and edges. The PMR

quadtree handles a collection of edges in the plane,

not necessarily forming a polygonal map, and uses a

probabilistic splitting rule. All such indexes maintain

a list of edges in the leaf blocks, but they do not en-

code the topological structure of the map. Thus, they

are good for searching in space but not for topological

navigation. The PM2-Triangle quadtree deﬁned here

is a triangle-based extension of an index in the class

of PM-quadtrees, namely the PM2-quadtree.

The K-structure (Kirkpatrick, 1983) is a spatial in-

dex for triangle meshes, developed in computational

geometry with the purpose of performing point loca-

tion in a triangle mesh in worst-case logarithmic time

in the number of vertices. Unlike the PR- and PM-

quadtrees, the K-structure organizes the data to be

stored and not the embedding space. It consists of

a hierarchy of triangle meshes of logarithmic height

described as a directed acyclic graph. The hierarchy

is computed by starting from the given mesh and re-

peatedly eliminating an independent set of vertices of

low degree. Compared with the PM-quadtree, the

K-structure has a better worst-case behavior, but it

is more complex to implement and update (Samet,

2006).

3 THE PM2-TRIANGLE

QUADTREE

3.1 Space Subdivision

A PM2-Triangle quadtree (or PM2T-quadtree) is a hi-

erarchical spatial index for triangle meshes. As all

quadtrees, it recursively divides a square domain con-

taining the data into four blocks of the same size,

and the resulting nested subdivision is described as

a quaternary tree. The PM2-Triangle quadtree has a

triangle-based subdivision rule. The blocks of the ﬁ-

nal subdivision, i.e., the leaves of the tree, must satisfy

the following four validity conditions:

1. A leaf block may contain at most one vertex.

2. If a leaf block contains one vertex v, it intersects

only the triangles incident in v.

3. If a leaf block b does not contain any vertex, the

triangles intersecting b are all incident in an exter-

nal common vertex.

4. Leaf blocks are maximal (i.e., no four sibling

leaves can be merged into a valid leaf).

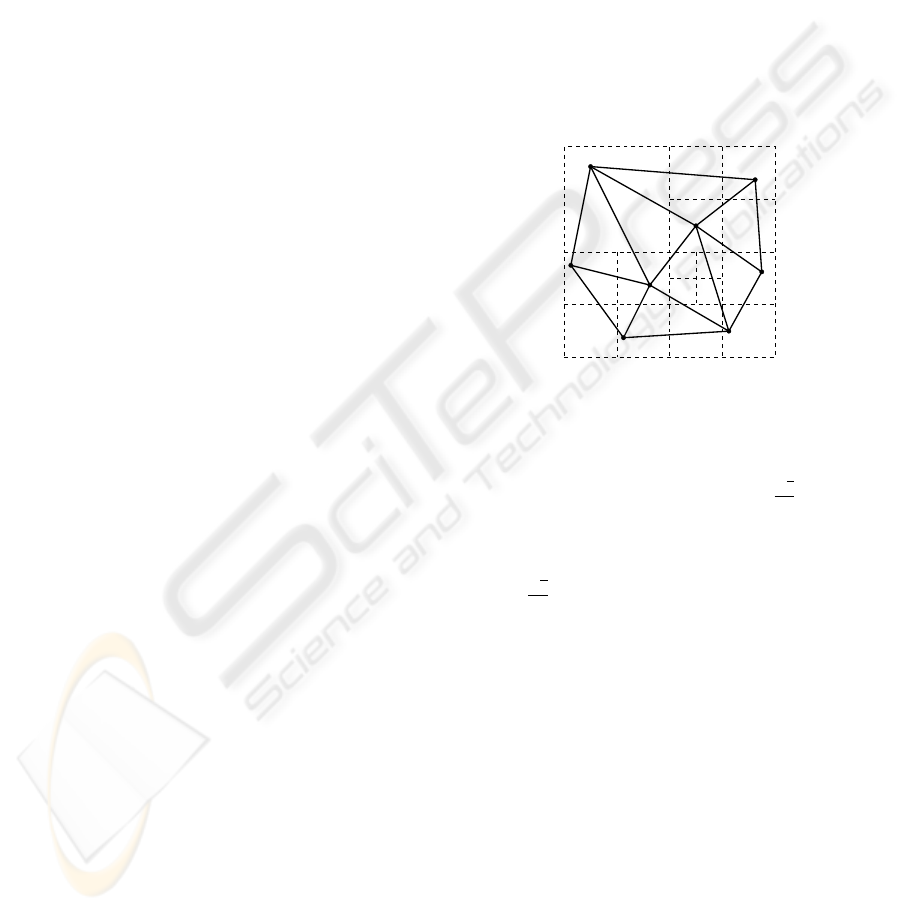
Figure 1 shows a PM2T-quadtree for a mesh of

eight triangles.

Figure 1: An example of a PM2T-quadtree.

Each validity condition provides an upper bound

in the evaluation of the depth of the tree. Condition

1 gives an upper bound D

= 1 + log

√

, where d

is minimum distance between any two vertices. Con-

ditions 2 and 3 imply an upper bound that depends

on the shape of the triangles, being equal to D

1 + log

√

where d

is the minimum height of the

triangles in the mesh. Thus, the global upper bound

to the depth of the PM2T-quadtree is max(D

Details can be found in (Facinoli et al., 2007).

3.2 Data Structure

We present a compact data structure for encoding the

PM2T-quadtree, which represents the combinatorial

structure of the triangle mesh and the structure of the

spatial index separately.

The combinatorial structure of the triangle mesh is

encoded through a triangle-based data structure, that

is the indexed data structure with adjacencies (De Flo-

riani and Hui, 2007). We encode the vertices and the

triangles of the mesh into a vertex array and a trian-

gle array, respectively. The index of the position in

the array is used to identify the triangle or the ver-

tex. The only geometrical information are the vertex

A HIERARCHICAL SPATIAL INDEX FOR TRIANGULATED SURFACES

coordinates and the vertex elevations. For each trian-

gle t, we encode the indexes of the three vertices of t

(Triangle-Vertex (TV) relation), and the indexes of the

three triangles adjacent to t along an edge (Triangle-

Triangle (TT) relation), ordered consistently with the

information in TV relation. For each vertex v, we en-

code the index in the triangle array of one of its inci-

dent triangles (partial Vertex-Triangle (VT) relation).

This is sufﬁcient to retrieve all the triangles incident

in a vertex v, in time linear in their number.

For encoding the structure of the spatial index,

we do not explicitly represent the quaternary tree that

describes the PM2T-quadtree through all nodes and

their parent-child pointers, but we encode only the

leaf nodes and their location codes. The location code

(Gargantini, 1982) of a leaf n describes the position

of n in the tree by means of the root-to-leaf path tra-

versed to reach it. Thus, for every leaf node, we store

its location code and an integer number, which al-

lows distinguishing among different types of leaves,

as well as retrieving the information (vertex and tri-

angles) possibly associated with such leaf. We have

the following types of leaves:

• An empty leaf is identiﬁed by the value −1.

• For a leaf block intersected by three or more tri-

angles, sharing a vertex v (that can be internal or

external to the block), we store the index of v. Tri-

angles are not explicitly stored since they are re-

trieved by using topological relations.

• For a leaf containing one triangle t, we store

a negative even integer content = −2(t + 1),

from which we can retrieve the index of t as

−(content/2) −1.

• For a leaf containing two triangles t

and t

, we

store a negative odd integer content = −2(t

1) + 1, if this quantity is different from −1 (al-

ready denoting an empty leaf); otherwise, it is

equal to the result of the same expression with t

instead of t

. The two triangles can be retrieved

one as ((1−content)/2) −1, and the other one as

its adjacent triangle which intersects the leaf.

We denote with N the number of vertices of the

triangle mesh, with T the number of its triangles

and with L

the number of leaf nodes in the PM2T-

quadtree. We consider every base type element (in-

tegers and pointers) to have a unit cost. The cost of

encoding the vertex coordinates and elevation values,

and the partial VT relation is equal to 4N, while the

cost of encoding the triangle array, i.e., the TV and

TT relations is equal to 6T . Finally the cost of encod-

ing the tree structure is equal to 2L

. This leads to

4N + 6T +2L

stored information items.

Note that 4N + 6T is the space required for rep-

resenting just the triangle mesh in a triangle-based

data structure, while 2L

expresses the overhead of

the spatial index. From Euler formula, T ' 2N. From

our experiments, L

is about 6N on average for syn-

thetic data, and about 5N for real data (see Section

4). Thus, the additional memory needed by the spa-

tial index is from 63% to 75% the memory required

for storing the triangle mesh itself.

4 ANALYSIS

We compare the PM2T-quadtree with other two spa-

tial indexes: the PM2-quadtree (Samet, 2006) for

polygonal maps, which can be used for a triangle

mesh as well, and an extension of the PR-quadtree

to triangle meshes.

We evaluate the space subdivision generated by

the different spatial indexes, the storage costs of

the data structures, and the performance on spatial

queries. The main requirement for a spatial in-

dex is to perform spatial queries efﬁciently, while

a low overhead of the data structure is desirable as

an additional requirement. Experiments show that

the PM2T-quadtree outperforms the other considered

spatial indexes in queries, and the proposed data stuc-

ture makes it compact enough.

We present results on synthetic data (De-

launay triangle meshes built on randomly gen-

erated point sets) and on triangulated mod-

els from the AIM@SHAPE shape repository

(http://shapes.aim-at-shape.net/): City of

Rome (957,456 vertices, 1,914,867 triangles), and

Dolomites mountains (810,000 vertices, 1,619,963

triangles).

4.1 Other Spatial Indexes

The PM2-quadtree belongs to the class of PM-

quadtrees (Samet, 2006) developed for polygonal

maps. In a PM2-quadtree, a leaf block contains at

most one vertex. If a leaf block contains a vertex,

it may intersect only edges incident in such vertex.

If a leaf block contains no vertex, it may intersect

only edges that meet a common vertex exterior to the

block. Each leaf has a list of edges intersecting it.

A PM2-quadtree, applied to a triangle mesh, rep-

resents the edges and not the triangles. The data struc-

ture we have implemented for the PM2-quadtree is

slightly different from the one described in (Samet,

2006). The vertices and edges of the map are stored

in a vertex array and an edge array, respectively. For

each vertex, we store its coordinates and elevation

value, and, for each edge, we store the indexes of its

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

two endpoints. This latter is the only topological in-

formation encoded in the PM2-quadtree. Each leaf

block stores its location code, and the list of the edges

intersecting the leaf block. The storage cost of a PM2-

quadtree is equal to 3N + 2E + 2L

+ 2E

, where E

denotes the number of edges and E

the total length

of all edge lists. Note that the number of leaves L

greater here than in the PM2T-quadtree (as shown in

Section 4.2), moreover E

≥ E and, from Euler for-

mula, E ' 3N in the case of a triangle mesh.

We have developed in (Facinoli et al., 2007) the

PM3-Triangle quadtree, or PM3T-quadtree, as an ex-

tension of the PR-quadtree for triangle meshes. It is

basically a PR-quadtree built on the mesh vertices,

where, in addition, each leaf stores all triangles it in-

tersects. Figure 2 shows the PM3T-quadtree built on

the same triangle mesh used for the PM2T-quadtree in

Figure 1. The depth of a PM3T-quadtree is inversely

proportional to the minimum distance between two

vertices in the mesh since the subdivision criterion is

only based on the position of vertices.

Figure 2: Example of a PM3-Triangle quadtree.

Note that, in a PM2T-quadtree, all triangles inter-

secting a leaf block are incident in a common vertex,

while this is not true for a PM3T-quadtree. Thus,

we are not able to ﬁnd all such triangles just from

the vertex, by using topological relations, as we did

in the PM2T-quadtree. Therefore, we need an ex-

plicit list of the triangles intersecting each leaf. The

data structure for the PM3T-quadtree stores, for each

non-empty leaf block, its location code, the vertex it

contains, and a list of the triangles that it intersects.

Vertices are encoded with their coordinates and el-

evations, while for each triangle only the Triangle-

Vertex (TV) relation is encoded, i.e., its three ver-

tex indexes. The storage cost of this data structure is

equal to 3 N + 3T + 3L

+ 2T

, where T

denotes the

total length of all triangle lists. Note that the number

of leaves L

of a PM3T-quadtree is lower than that

of a PM2T-quadtree (as shown in Section 4.2), while

≥ T ' 2N.

4.2 Structure of the Subdivision

We compare the domain subdivisions provided by the

PM2T-quadtree, the PM2 quadtree and the PM3T-

quadtree, on the same triangle mesh.

The domain subdivision induced by a PM2-

quadtree may be ﬁner than the one induced by a

PM2T-quadtree. Consider a leaf block b with an as-

sociated vertex v. If b is intersected by the third edge

e of a triangle t incident in v, this causes a subdivi-

sion of b in the PM2-quadtree. On the contrary, the

PM2T-quadtree does not subdivide b because it con-

siders edge e as part of triangle t (see Figure 3). Note

that this situation can only happen near the bound-

ary of the domain of the triangle mesh. In the inte-

rior of the mesh, such a leaf node b would be subdi-

vided in the PM2T-quadtree as well, because of the

other triangle adjacent to t along edge e. On the other

hand, the subdivision induced by a PM2-quadtree

cannot be coarser than the one induced by a PM2T-

quadtree. The subdivision rule of the PM2T-quadtree

is a triangle-based version of the edge-based rule used

in the PM2-quadtree. Whenever the PM2T-quadtree

splits a block because of a triangle t intersecting it,

necessarily at least one edge of t intersects the same

block, thus splitting it in the PM2-quadtree as well

(see (Facinoli et al., 2007) for a complete proof).

v v

e e

(a) (b)

Figure 3: The PM2-quadtree (b) produces a ﬁner subdivi-

sion than the PM2T-quadtree (a).

The subdivision induced by a PM2T-quadtree

is ﬁner than the subdivision induced by a PM3T-

quadtree on the same triangle mesh (see Figures 1 and

2). This is due to the fact that, in a PM3T-quadtree,

the triangles associated with a leaf block do not nec-

essarily need to share a common vertex.

Figures 4 and 5 compare the depth and the num-

ber of leaf blocks in the three indexes, expressed as a

function of the number of the mesh vertices, for syn-

thetic data sets. Table 1 shows the results for real data.

The PM2-quadtree is at least as deep as the PM2T-

quadtree, and the number of its leaf blocks is about

25% more than in a PM2T-quadtree, on average. As

expected, a PM3T-quadtree is less deep than the other

two indexes and has fewer leaf blocks. In particular,

the PM3T-quadtree depth is about 90%, and its leaves

are about 30%, than in the PM2T-quadtree.

A HIERARCHICAL SPATIAL INDEX FOR TRIANGULATED SURFACES

On the other hand, our experiments in (Facinoli

et al., 2007) show that the number of triangles inter-

secting a leaf block are about 150% higher in a PM3T-

quadtree than in a PM2T-quadtree. This leads to

larger memory requirements for the PM3T-quadtree,

in spite of the coarser subdivision (see Section 4.3).

0 1 2 3 4 5

x 10

number of vertices

depth

PM2T quadtree

PM2 quadtree

PM3T quadtree

Figure 4: Depth of the tree on synthetic data.

0 1 2 3 4 5

x 10

0.5

1.5

2.5

3.5

4.5

x 10

number of vertices

number of leaves

PM2T quadtree

PM2 quadtree

PM3T quadtree

Figure 5: Number of leaf nodes on synthetic data.

Table 1: Depth of the tree, number of leaf nodes, and stor-

age costs on real data.

index depth leaves storage (Mb)

Rome

PM2T 22 3,857,305 84.98

PM3T 12 1,397,315 95.56

PM2 12 3,895,022 166,72

Dolomites

PM2T 23 4,659,781 87.86

PM3T 12 1,146,715 116.96

PM2 13 4,707,102 237.58

4.3 Costs of the Data Structures

We consider here the space requirements of the data

structures for the PM2T-quadtree, the PM2-quadtree,

and the PM3T-quadtree.

Figure 6 compares the storage costs on synthetic

data. Results on real data are shown in Table 1.

The total cost of a PM2T-quadtree is about 3/4

than the total cost of a PM3T-quadtree. This happens

even if the domain subdivision in the PM2T-quadtree

is ﬁner than in a PM3T-quadtree (see Subsection 4.2).

Our experiments in (Facinoli et al., 2007) have shown

that the cost of storing the leaf nodes in a PM2T-

quadtree is almost 1/3 than in a PM3T-quadtree, be-

cause the leaves of a PM2T-quadtree do not store any

triangle list.

The storage cost of the PM2T-quadtree is about

40% of that of the PM2-quadtree, because the lat-

ter has a ﬁner domain subdivision, and furthermore

stores a list of edges in each leaf node. Our experi-

ments in (Facinoli et al., 2007) show that around 90%

of space in a PM2-quadtree is used for storing the leaf

nodes.

0 1 2 3 4 5

x 10

number of vertices

storage costs

PM2T quadtree

PM2 quadtree

PM3T quadtree

Figure 6: Storage costs (in Kbytes) for synthetic data.

4.4 Performance in Queries

We consider here the two triangle-based indexes,

namely the PM2-Triangle quadtree and the PM3-

Triangle quadtree.

The basic geometric query we consider here is

point location, i.e., ﬁnding the triangle(s) of the mesh

containing a given query point.

Other common queries are the window query and

the range query, i.e., ﬁnding all the triangles inter-

sected by a rectangular or a circular area. Thanks

to the fact that a PM2T-quadtree represents the con-

nectivity of the mesh, such queries can be answered

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

by performing a point location for the centroid of

the query region, and then navigating the triangle

mesh through adjacency relations, until all other in-

volved triangles have been found. The cost is equal

to the cost of point location plus a number of point-

in-triangle tests linear in the number of reported trian-

gles.

The algorithm for point location query descends

the tree down to the leaf b containing the query point

p, and then performs a point-in-triangle test for each

triangle associated with b. To verify if a triangle con-

tains p, we need to test which if p deﬁnes a left or

right turn with the three edges of the triangle. If

the triangles form a fan, some triangle edges can be

skipped because already tested while processing the

previous triangle of the fan. The most time consum-

ing operation is computing a turn (since it involves

ﬂoating-point arithmetics).

Point location on a PM2-quadtree is more com-

plex since the triangles are not represented. It requires

ﬁnding the edges of the triangle containing the point,

which implies nearest neighbor computations.

Table 2: Results for the point location query on real data.

Visited Visited Computed

Triangles Nodes Turns

Index avg var avg var avg var

Rome

PM2T 1.60 0.30 11.3 4.9 4.80 0.70

PM3T 2.55 3.02 10.50 3.83 6.66 14.50

Dolomites

PM2T 2.0 0.72 11.90 0.10 4.8 2.5

PM3T 3.10 2.32 10.90 0.10 7.70 11.34

We consider the number of nodes visited in the

tree traversal, the number of triangles checked for in-

clusion and the number of turns computed (see Table

2). The upper bound to the number of visited nodes

is the depth of the tree (see Figure 4). The number

of visited triangles and the number of turns computed

depend on the number of triangles incident in the leaf

node containing the query point p.

The number of visited nodes is lower in the PM3T-

quadtree, since it has a lower depth. The number

of tested triangles and turn computations, as well as

their variances, are lower in the PM2T-quadtree. This

means that the PM2T-quadtree performs better, al-

though the tree is deeper, since turn computations

have a dominat cost. Speciﬁcally, a lower variance

implies that the worst case performs better.

5 CONCLUDING REMARKS

We have presented a new spatial index for triangle

meshes, called PM2-Triangle quadtree. We have de-

ﬁned and implemented a compact representation for

a PM2T-quadtree based on the complete separation

of the combinatorial information on the triangle mesh

(needed to navigate in the mesh), and the structure of

the spatial index (used to reduce searching space in

queries). We have tested the efﬁciency of the PM2T-

quadtree through experiments.

Our current and future work is in spatial indexes

for tetrahedral meshes, for application to visualiza-

tion of 3D scalar ﬁelds and to ﬁnite element meshes.

The PM2-Triangle quadtree can be generalized into

a PM2-Tetrahedron octree, and a data structure for it

can be deﬁned based on the same idea of separating

the structure of the mesh and the structure of the spa-

tial index.

REFERENCES

De Floriani, L. and Hui, A. (2007). Shape representations

based on cell and simplicial complexes. In State-of-

the-Art Report (STAR), Eurographics, Prague.

Facinoli, M., De Floriani, L., Dimitri, D., and Magillo,

P. (2007). The PM2-Triangle quadtree: a hierarchi-

cal spatial index for terrain modeling. Technical re-

port, Department of Computer and Information Sci-

ence, University of Genova (Italy).

Gargantini, I. (1982). An effective way to represent

quadtrees. Communications of the ACM, 25(12):905–

910.

Kirkpatrick, D. (1983). Optimal search in planar subdivi-

sions. SIAM Journal on Computing, 12(1):28–35.

ucke, E., Saias, I., and Zhu, B. (1999). Fast random-

ized point location without preprocessing in two- and

three-dimensional delaunay triangulations. Computa-

tional Geometry, 12((1-2)):63–83.

Orenstein, J. A. (1982). Multidimensional tries used for

associative searching. Information Processing Letters,

14(4):150–157.

Samet, H. (2006). Foundations of Multi-Dimensional

and Metric Data Structures, chapter 1.4. Morgan-

Kaufmann.

A HIERARCHICAL SPATIAL INDEX FOR TRIANGULATED SURFACES