
GEOMETRICAL
DEGENERACY REMOVAL BY VIRTUAL
DISTURBANCES
An Application to Surface Reconstruction from Point Slice Samples
Oscar Ruiz
CAD CAM CAE Laboratory, EAFIT University, Medellin, Colombia
Eliana Vasquez
1
, Sebastian Pe
˜
na
2
, Miguel Granados
3
1
Erasmus Universitaet, Nederlands
2
Fraunhofer Inst. Comp. Graphics, Germany
3
Max Planck Inst. Informatiks, Germany
Keywords:
Geometric degeneracy, Voronoi diagram, Delaunay triangulation, surface reconstruction, slice point sample.
Abstract:
In surface reconstruction from slice samples (typical in medical imaging, coordinate measurement machines,
stereolithography, etc.) the available methods attack the geometrical and topological properties of the surface.
Topological methods classify the transitions occurred in the 2-manifold between two consecutive slices i and
i + 1. Geometrical methods synthesize the surface based on local proximity of the contours in consecutive
slices. Superimposed 2D Voronoi Diagrams V D
i
and VD
i+1
for slices i and i + 1, respectively, present topo-
logical problems if, for example, a site of V D
i
lies on an site or an edge of V D
i+1
. The usual treatment of
this problem in literature is to apply a geometrical disturbance to either V D
i
or V D
i+1
, thus eliminating the
degeneracy. In contrast, this article presents the implementation of a method which identifies the degener-
ate situation, constructs un-instantiated topological constructs, choses a geometrical instantiation based on a
virtual disturbance introduced to the actual configuration. The algorithm was successfully applied to remove
non-manifold topologies produced by well known algorithms in surface reconstruction.
1 INTRODUCTION
Degenerate conditions in geometric algorithms have
been dealt with different ways: (i) by stating the
same problem in different spaces with better condi-
tioning, (ii) by increasing the real computation pre-
cision, (iii) by relying on rational numbers, with no
rounding errors, and (iv) by disturbing the input for
the geometrical algorithms, while at the same time
estimating the probability of respecting the original
problem topology. Strategies (i) and (ii) have been
extensively applied in Numerical Analysis, for ex-
ample, by generating equivalent linear systems with
better manipulation properties. Alternative (iii) has
been investigated, for example in Computational Ge-
ometry Algorithm Library (Burnikel et al., 1999),
with exact computation paradigms. Strategy (iv) has
given probability bounds for alteration of Voronoi-
Delaunay topology upon numerical disturbance of de-
generate events (Funke et al., 2005). Virtual Perturba-
tions have been used in other contexts (Edelsbrunner
and M
¨
ucke, 1990). It should be noticed that none of
the mentioned strategies solves the degeneracy prob-
lem. Each is suited for a particular domain of prob-
lems.
The strategy presented here assumes the possibil-
ity of detecting the degenerate condition, and to cre-
ate a finite number of topological configurations for
the solution. The geometrical and topological objects
created are not numerically instantiated, until the very
end of the proposed scheme. The strategy presented
here is clearly convenient when there is a finite num-
ber of topological configurations, which can be enu-
merated and distinguished.
The particular context in which this strategy is
presented is the general problem of surface recon-
struction, from planar samples. Particular steps of
the Boissonat & Geiger algorithm (Boissonnat, 1988;
Geiger, 1993) have been changed in order to make
them more robust (Ruiz et al., 2002; Ruiz et al., 2005).
Section 2 gives the application context of the present
work and reviews related literature. Section 3 de-
113
Ruiz O., Vasquez E., Peña S. and Granados M. (2008).
GEOMETRICAL DEGENERACY REMOVAL BY VIRTUAL DISTURBANCES - An Application to Surface Reconstruction from Point Slice Samples.
In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 113-118
DOI: 10.5220/0001098101130118
Copyright
c
SciTePress
scribes the methodology applied and the procedures
followed. Section 4 gives an account of the results,
and section 5 concludes the article.
2 CONTEXT AND LITERATURE
REVIEW
The scenario to apply the proposed algorithm for de-
generacy control is the following: Consider a solid
object B, whose boundary M = ∂B is a smooth 2-
manifold or shell in R
3
. Consider a set of parallel
planes Π
i
, i = 0, 1, 2, ... sectioning M, and therefore
producing traces of M which are Jordan curves Γ
j,i
or contours drawn on the planes Π
i
. Recovering M
from the contour set boils down to recovering M
i,i+1
,
the portion of M contained between the planes Π
i
and
Π
i+1
.
The algorithm proposed and implemented by
Boissonat & Geiger in (Boissonnat, 1988; Geiger,
1993) (called here B+G ) builds tetrahedra filling the
space between two consecutive sampling planes i and
i + 1. B+G is a fairly fast and robust algorithm, origi-
nally presenting weaknesses that have been corrected
by complementary works ((Ruiz et al., 2005)). The
boolean union of such tetrahedra produces the por-
tion of the solid contained between the planes i and
i + 1. B+G basically uses local geometrical proximity
between contours to construct the surface M
i,i+1
. As
a consequence, over-stretched surfaces may be gener-
ated joining contours on the planes i with those on
plane i + 1 which have little to do with each other
in the global sense. This effect may be diminished
by applying a 2D shape similarity (2DSS) algorithm
(Ruiz et al., 2002; Ruiz et al., 2005). In B+G, the
tetrahedra are built by projecting the Voronoi Dia-
gram (VD) of the point set in level i, VD
i
, onto V D
i+1
,
or vice versa. A degeneracy condition for B+G occurs
when a Voronoi site of V D
i
exactly lies on either a
Voronoi site or a Voronoi edge of V D
i+1
. Such a con-
dition produces a non-manifold and self - intersection
condition in the surface built by B+G. The work pre-
sented in this article corresponds to the application
of late numerical instantiation of topological and ge-
ometrical objects to solve such a degeneracy.
2.1 Brief Review of the B+G Method
The B+G method divides the interior of the contours
in triangles by creating the Delaunay Triangulation of
the contour vertices (figures 2 and 3). After some pro-
cessing, the Voronoi Diagrams belonging to the lev-
els are used to create a planar graph named the Joint
Voronoi Diagram (figure 4). This graph states how
1 2
3
A
B
C
Π
i
Π
i+1
Figure 1: Original contours.
VE
31
DV
3
VE
23
DV
2
VV
123
VE
12
DV
1
Figure 2: Delaunay Triangulation and Voronoi Diagram of
the contours.
DV
B
DV
A
VV
ABC
VE
AB
VE
CA
VE
BC
DV
C
Figure 3: Delaunay Triangulation and Voronoi Diagram of
the contours.
T
1
T
12
T
12
T
2
Figure 4: Delaunay Triangulation and Voronoi Diagram of
the contours.
Figure 5: Related tetrahedrons.
the triangles in the levels are linked, by translating
then to tetrahedrons (figure 5). Finally the triangles
of the tetrahedrons facing the exterior are taken as the
reconstructed surface.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
114

3 IMPROVEMENTS ON THE B+G
METHOD
The Polyhedral Surface Method, presented here an
in (Ruiz et al., 2005) is based on the B+G method.
In the following discussion it will be shown that the
B+G method may reconstruct incomplete surfaces
and present non manifold situations. With our method
the non manifold situations are minimized by preemp-
tively considering special configurations of the Joint
Voronoi Diagram (section 3.1).
3.1 Special Cases in the Creation of the
Joint Voronoi Diagram
The Joint Voronoi Diagram of two consecutive levels
results from intersecting the orthogonal projections
of their Voronoi Diagrams on a common plane. The
Joint Voronoi Diagram is formed by three kinds of
nodes: T
1
, T
2
and T
12
. The T
1
and T
2
nodes correspond
to the Voronoi vertices belonging to the Voronoi Dia-
gram on levels i or i + 1. The T
12
nodes correspond to
the intersection of Voronoi edges, coming from levels
i or i + 1.
Every node in the graph corresponds to a tetrahe-
dron, and the union of all these tetrahedrons forms the
3D Delaunay Diagram of the contour points P on both
levels i and i + 1. Because the tetrahedrons that are
translated from the graph are Delaunay tetrahedrons,
they satisfy the “empty-sphere” condition, namely is,
the sphere that circumscribes the tetrahedron does not
contain any other point in P except its vertices.
Each tetrahedron is created with four Delaunay
vertices. See figure 5 where a T
1
, T
2
and two T
12
tetrahedrons are translated from the Joint Voronoi Di-
agram in figure 4.
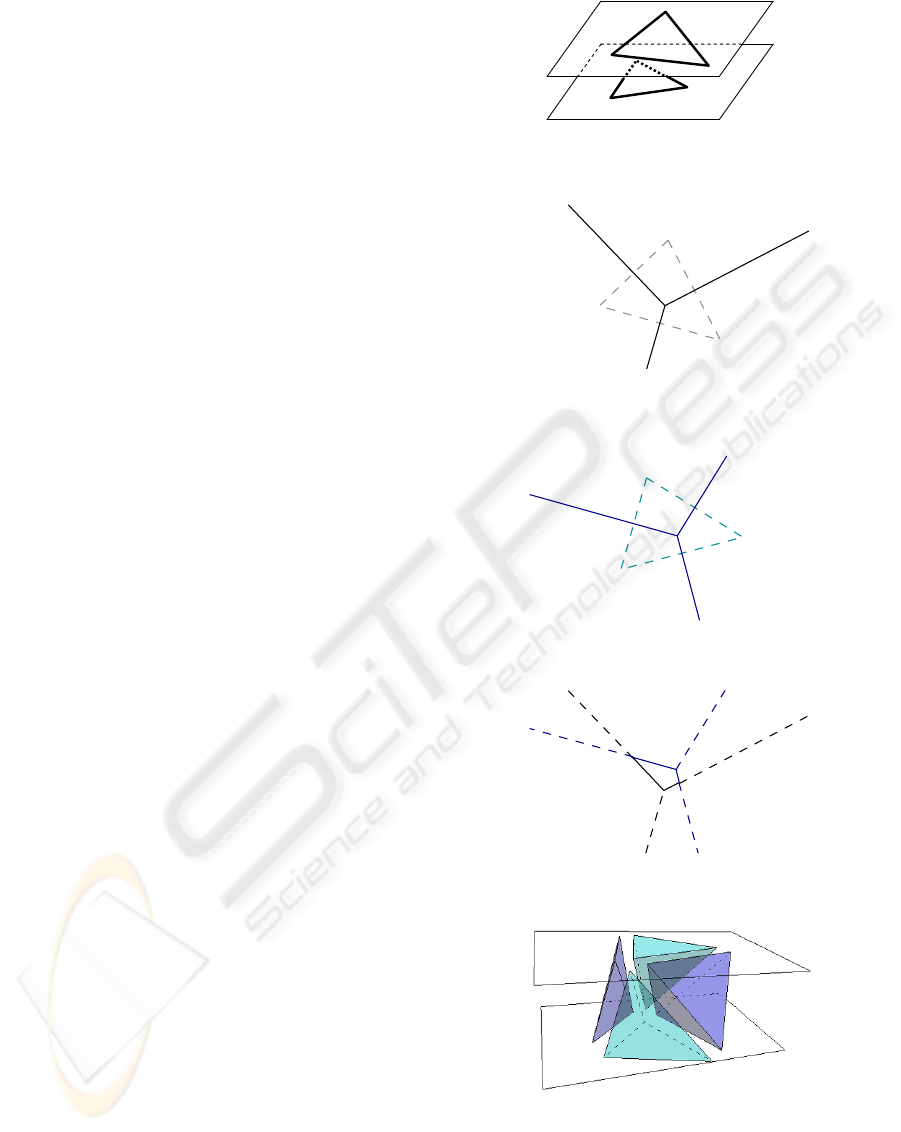
3.1.1 Case 1: Voronoi Vertex Vs. Voronoi Edge
When five Delaunay vertices are co-spherical (Figure
6), a Voronoi vertex belonging to level i is exactly
projected on a Voronoi edge belonging to level i + 1,
or vice versa (Figure 7).
The solution for such a degenerate condition is to
pretend that VV
123
is either above or below Voronoi
edge VV
ABD
←→ VV
BCD
. For the first alternative, the
virtual configuration appears in Figure 8, and its spa-
tial consequence is displayed in Figure 9. For the sec-
ond alternative, the virtual configuration is shown in
Figure 10, while its spatial consequence appears in
Figure 11.
DV
1
DV
2
DV
3
DV
B
DV
C
DV
D
DV
A
Figure 6: Voronoi vertex vs. Voronoi edge case. Vertices
DV
1
, DV
2
, DV
3
, DV
B
and DV
D
are co-spherical.
DV
1
DV
3
DV
2
DV
A
DV
C
DV
D
DV
B
VE
31
VE
12
VE
23
VE
AB
VE
BC
VE
CD
VE
AD
Figure 7: Voronoi vertex vs. Voronoi edge case. Join
Voronoi Diagram of levels i and i + 1.
VE
31
VE
12
VE
BC
VV
123
VE
DA
VE
AB
VV
ABD
VV
BCD
VE
BD
VE
CD
VE
23
Figure 8: Voronoi vertex vs. Voronoi edge case. Delaunay
vertex DV
D
elected as apex.
Figure 9: Voronoi vertex vs. Voronoi edge case. Spatial
Configuration.
VE
12
VV
123
VE
31
VE
DA
VV
ABD
VE
AB
VE
BC
VV
BCD
VE
CD
VE
23
Figure 10: Voronoi vertex vs. Voronoi edge case. Delaunay
vertex DV
B
elected as apex.
GEOMETRICAL DEGENERACY REMOVAL BY VIRTUAL DISTURBANCES - An Application to Surface
Reconstruction from Point Slice Samples
115
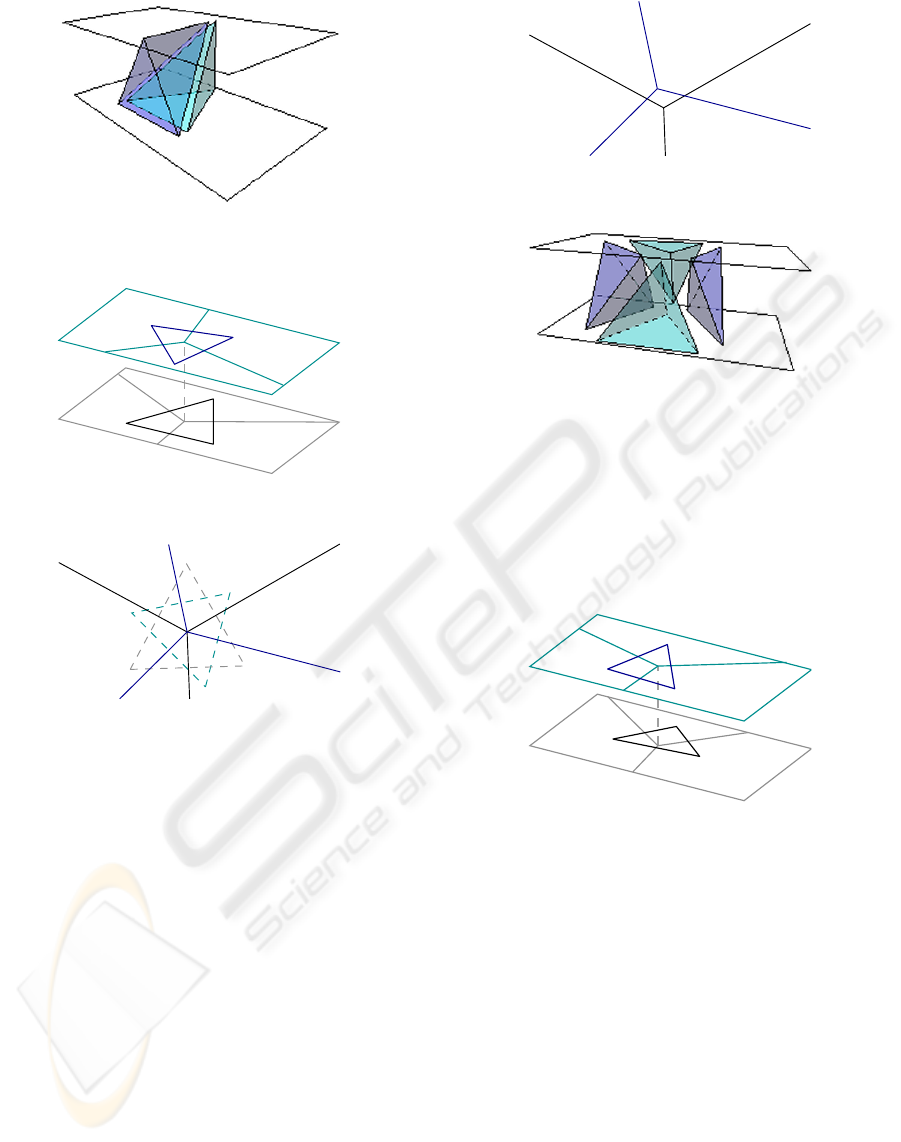
Figure 11: Voronoi vertex vs. Voronoi edge case. Delaunay
vertex DV
B
elected as apex.
D
V
1
DV
2
DV
3
D
V
B
DV
A
DV
C
Figure 12: Voronoi Vertex vs. Voronoi Vertex case. Sub-
case 1a2b3c.
VE
CA
DV
1
VV
ABC
DV
C
VE
31
VE
BC
DV
3
DV
B
VE
23
VV
ABC
DV
2
VE
AB
DV
A
VE
12
Figure 13: Voronoi Vertex vs. Voronoi Vertex case. Sub-
case 1a2b3c. Projection of Voronoi Diagrams of levels i
and i + 1.
3.1.2 Case 2: Voronoi Vertex Vs. Voronoi Vertex
This case occurs when six Delaunay vertices are co-
spherical. As a result, a Voronoi vertex of level i is
projected onto a Voronoi vertex of level i + 1.
The sub-cases are determined by the distribution
of the edges on the “intersecting star” created when all
the edges are projected on the same plane (see figure
12 to 17 ). There are only two possible distributions.
(a) the edges are intercalated or (b) they are not. When
two consecutive edges belong to the same level, the
sub-case is identified as the 1ab23c sub-case. If there
are no two consecutive levels belonging to the same
level, the sub-case is identified as the 1a2b3c one.
The sub-case 1a2b3c appears in Figure 12. The
Joint Voronoi Diagram for the levels i and i + 1 ap-
pears in Figure 13. The virtual disturbance to solve
this degeneracy appears in Figure 14, while its spatial
effects do so in Figure 15.
VE
12
VE
23
VE
31
VV
123
VE
CA
VE
AB
VV
ABC
VE
BC
Figure 14: A virtual disturbance for the 1a2b3c. sub-case.
Figure 15: Spatial consequence for the virtual disturbance
of Figure 14.
For the same situation, the sub-case 1ab23c ap-
pears in Figure 16. For this case, the projection of the
Voronoi Diagrams onto each other is seen in Figure
17. The virtual disturbances to solve this problem are
shown in Figures 18, 19 and 20. A spatial configura-
tion for one of such virtual scenarios appears in 21.
DV
1
DV
2
D
V
3
DV
B
D
V
C
DV
A
Figure 16: Voronoi Vertex vs. Voronoi Vertex case. 1ab23c
sub-case.
4 RESULTS
As said before, the special cases dealt with here are
generated when more than four Delaunay vertices
lie on the surface of an empty sphere. In the B+G
method this situation leads to non-manifold surfaces,
like the one shown in figure 22. The virtual perturba-
tions proposed here avoid the uncertainty of the B+G
method (which uses random numerical disturbances).
Such virtual perturbations produce an improved re-
sult, shown in figure 23. Results for the Skull data set
(figure 24) are shown in figure 25. The results for the
data set Brain are shown in Figures 26 and 27. Other
examples will be published in more extended reports
of this investigation.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
116
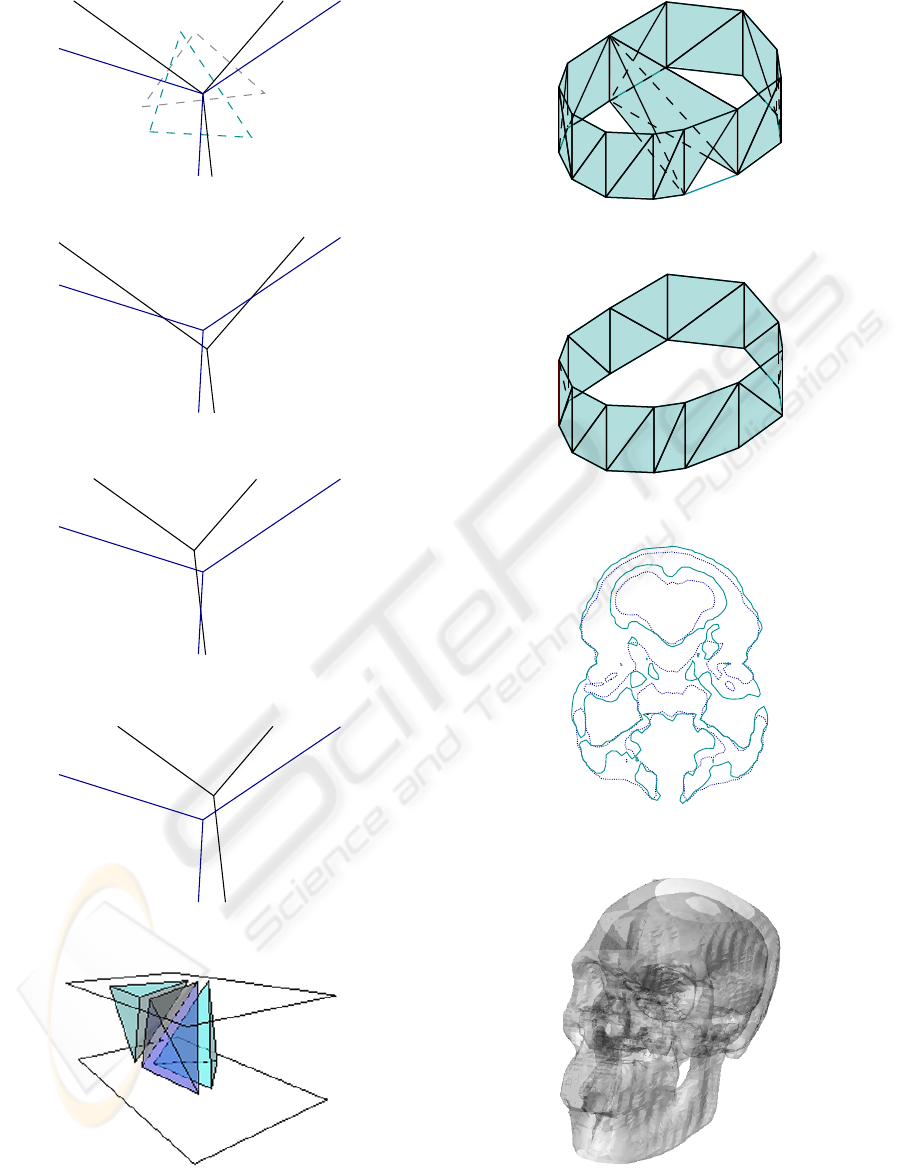
DV
2
DV
3
DV
B
DV
C
VE
31
DV
1
DV
A
VE
12
VE
23
VV
123
VE
AB
VV
ABC
VE
BC
VE
CA
Figure 17: Voronoi Vertex vs. Voronoi Vertex case. 1ab23c
sub-case.
VE
12
VV
123
VE
23
VE
31
VE
AB
VE
CA
VE
BC
VV
ABC
Figure 18: Virtual disturbance for the 1ab23c sub-case. So-
lution with three T
12
.
VE
12
VV
123
VE
23
VE
31
VE
CA
VE
AB
VV
ABC
VE
BC
Figure 19: Virtual disturbance for the 1ab23c sub-case. So-
lution with two T
12
.
VE
12
VE
23
VE
31
VV
123
VE
AB
VV
ABC
VE
CA
VE
BC
Figure 20: Virtual disturbance for the 1ab23c sub-case. So-
lution with just one T
12
.
Figure 21: A spatial configuration for the 1ab23c. sub-case.
Figure 22: Surface reconstructed using the B+G method di-
rectly.
Figure 23: Surface reconstructed by the virtual disturbance
method.
Figure 24: Detail of levels i and i + 1 of the set of contours
“skull”.
Figure 25: Reconstructed surface in a transparent material.
GEOMETRICAL DEGENERACY REMOVAL BY VIRTUAL DISTURBANCES - An Application to Surface
Reconstruction from Point Slice Samples
117
Figure 26: Set of contours.
Figure 27: Reconstructed surface in a transparent material.
5 CONCLUSIONS
A method has been designed and implemented, to
circumvent geometrical degeneracies arising from si-
multaneous processing of 2D superimposed Voronoi
Diagrams, in the context of Surface Reconstruction
from Slice Samples. In this particular problem, for
each degenerate condition an enumerable finite set of
non-degenerate counterparts is programmed, and in-
stantiated as the geometry of the degeneracy dictates.
In absence of the algorithm, self-intersecting and
therefore non - manifold constructions are produced.
With the algorithm, degenerate cases are mapped to
their non - degenerate counterparts. This allows the
normal downstream execution of the host algorithm
(B+G, by Boissonnat & Geiger, 1988, 1993). The
method presented classifies actions to be taken, based
on the level of the degeneracy. The results show that
the method is successful in removing the degeneracy,
without further iterations and in a deterministic way.
This method can be applied when the number of cases
of degeneracy is known.
REFERENCES
Boissonnat, J. D. (1988). Shape reconstruction from planar
cross-sections. Computer Vision, Graphics and Image
Processing, pages 1–29.
Burnikel, C., Fleischer, R., Mehlhorn, K., and Schirra, S.
(1999). Efficient exact geometric computation made
easy. In Proceedings of the 15th Annual ACM Sympo-
sium on Computational Geometry.
Edelsbrunner, H. and M
¨
ucke, E. P. (1990). Simulation
of Simplicity: A technique to cope with degenerate
cases in geometric algorithms. ACM Transactions on
Graphics, 9(1):66–104.
Funke, S., Klein, C., Mehlhorn, K., , and Schmitt, S. (2005).
Controlled perturbation for delaunay triangulations.
In Proceedings of S.O.D.A.
Geiger, B. (1993). Three dimensional modeling of hu-
man organs and its application to diagnosis and surgi-
cal planning. Research Report 2105, INRIA, Sophia-
Antipolis, Valbonne, France.
Ruiz, O., Cadavid, C., and Granados, M. (2002). Evalu-
ation of 2d shape likeness for surface reconstruction.
Journal Anales de Ingenieria Grafica, (15):16–24.
Ruiz, O., Cadavid, C., Granados, M., Pe
˜
na, S., and Vasquez,
E. (2005). 2d shape similarity as a complement for
voronoi-delone methods in shape reconstruction. El-
sevier Computer and Graphics, 29(1):81–94.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
118
