A FULLY GPU-IMPLEMENTED RIGID BODY SIMULATOR

Álvaro del Monte, Roberto Torres, Pedro J. Martín and Antonio Gavilanes

Dpto. Sistemas Informáticos y Computación, Universidad Complutense de Madrid, Spain

Keywords: Physically based animations, Graphics Processing Units.

Abstract: In this paper we study how to implement a fully GPU-based rigid body simulator by programming shaders

for every phase of the simulation. We analyze the pros and cons of different approaches, and point out the

bottlenecks we have detected. We also apply the developed techniques to two case studies, comparing them

with the analogous versions running on CPU.

1 INTRODUCTION

The study of animation techniques has played a

decisive role in the evolution of computer graphics.

Traditionally in this topic, the issue of the physically

based motion of rigid bodies has been one of the

most attractive areas, mainly due to the high level of

realism achieved when rendering the involved

scenes. Since precision usually competes against the

run-time cost, most rigid body simulators have

specialized in configurations that get a trade-off

between accuracy and efficiency. However, it is

common to most of them to implement two phases

to solve two tasks: collision detection and collision

response. The first one looks for contacts between

pairs of objects, and it is usually split in other two

phases: the broad phase and the narrow phase. The

broad phase applies bounding volumes to objects in

order to check whether bounding volumes collide or

not (Teschner et al., 2005). If a pair collides, the

narrow phase determines if the included objects are

in collision. Only after determining that there will be

a real collision, the collision points are calculated.

The reason to decompose collision detection in these

two phases is that broad phase algorithms have a

much lower cost than those involved in the narrow

phase. Apart from these software solutions, there are

also other collision detection approaches which use

specific hardware (Raabe et al., 2006).

Different techniques have been proposed to deal

with the collision response. Although some

implementations allow interpenetration of objects,

such as the penalty method (McKenna and Zeltzer,

1990), most of them try to avoid it by accurately

computing the instant the impact comes up. This can

be achieved with the classic bisection method

(Baraff, 1997): the interval in which the collision

takes place is gradually reduced by comings and

goings in time. Once the collision instant is

computed, the response can be obtained by applying

the forces which solve certain constraints −Baraff’s

constraint method (Baraff, 1989)− or by

instantaneously modifying the velocity of the objects

after computing the related impulse (Mirtich, 1996).

The efficiency of a rigid body simulator does not

only depend on the components integrating the

system, but also on the way they are integrated into

the simulation loop, especially when a large number

of objects are involved. Note that the collision time

of a pair of objects can affect to –even avoid– many

other collisions that come up later in the same loop

iteration. For this reason, the computation of the

instant for these other collisions is a useless task that

could collapse the simulation as a whole. In order to

prevent this eventuality, in a uniprocessor context,

(Mirtich, 2000) proposed the timewarp algorithm

which uses heaps as data structures.

On other hand, the evolution of GPUs, as regards

performance and programmability, has brought

about their intensive use in many applications.

Today they are a key element in the design stage of

any simulator. This is the case for the interactive

visualization of particle systems (Krüger et al.,

2005), where GPUs have been used to parallelly

manage the independent movement of each particle.

In the context of rigid body simulations, shaders

have been used to relieve CPU of specific tasks, but

never to solve the whole algorithm. For instance

(Yuksel, 2007) introduces fragment shaders in the

rendering phase to quickly support special effects,

342

del Monte Á., Torres R., J. Martín P. and Gavilanes A. (2008).

A FULLY GPU-IMPLEMENTED RIGID BODY SIMULATOR.

In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 342-350

DOI: 10.5220/0001098503420350

 SciTePress

while all the computations involved in the

simulation part are implemented on the CPU.

Concerning the simulation methodology, moving the

detection of collisions to GPU has been the most

studied topic. Collision detection algorithms on

GPUs can be classified into two categories. On one

hand, screen-space approaches use the depth or

stencil buffers to perform the collision tests by

rendering the geometry primitives (Govindaraju et

al., 2005) (Teschner et al., 2005). Their main

problems are that effectiveness is often limited by

the image space resolution, and that only potentially

colliding pairs are reported, so another test must be

applied on the CPU later.

On the other hand, object-space approaches use

the floating point bandwidth and programmability of

modern GPUs to implement the collision test.

(Zhang and Kim, 2007) performs massively-parallel

pairwise, overlapping tests onto AABB streams,

although exact primitive-level intersection tests are

performed on CPU. (Greβ and Zachmann, 2004)

(Horn, 2005) (Greβ et al., 2006) generate bounding

volume hierarchies on the GPU from a geometry

imaged (Gu et al., 2002) representation of the solids.

In order to expose the parallel processing

capabilities of the GPU, they breadth-first traverse

these hierarchies by using the non-uniform stream

reduction presented in (Horn, 2005). Nevertheless,

these approaches cannot autonomously operate on

the GPU, since the selection of the objects of the

pair to be tested is usually chosen on the CPU.

Furthermore, they do not apply any response when

the objects actually collide, so they should require

extra CPU collaboration to address interactions.

In the context of deformable objects, recent

papers have used the GPU capabilities to quickly

update their geometry: (Pascale et al., 2005)

proposes the use of vertex shaders to locally deform

the object, (Zhang and Kim, 2007) employs a

fragment shader to update the AABB streams, and

(Kim et al., 2006) uses a fragment shader to compute

the mass properties of rigid bodies in a buoyancy

simulation. Nevertheless, none of these papers cover

interactions between objects.

In this paper we study how to implement a fully

GPU-based rigid body simulator, by programming

shaders for every phase of the simulation. We

analyze the pros and cons of different approaches,

and point out the bottlenecks we have detected. We

also apply the developed techniques to two case

studies, comparing them with the analogous versions

running on CPU.

2 THE SIMULATION LOOP

The animation in a rigid body simulation is achieved

through a main loop, which updates the information

related to every object, after a cycle or step has been

completed. The size of the step must be accurately

chosen because of stability reasons. So the realism

level of the simulation directly depends on it.

In order to complete a step, the dynamics of

every object (position of its center of mass

x(t),

orientation

r(t), linear velocity v(t), and angular

velocity ω(t)) must be updated by using numerical

methods to solve ordinary differential equations.

Figure 1 shows both the configuration

Y(t) of the

state of an object and its time derivative in a 2D

scenario. In this case, the vector

r(t) and ω(t)

can be simplified to single scalars. Velocities change

according to the action of forces, since there exist

simple relations between their time derivatives and

the applied forces. The torque generated by a force

F(t) is defined as τ(t) = (p-x(t))×F(t),

where p is the location at where F(t) acts. Again

the vector

τ(t) can be simplified to a single scalar

in a 2D scenario. The mass M and the moment of

inertia

I are two scalars expressing the resistance of

a body to a linear or an angular motion, respectively.

The collision computation is the main task

involved in each step, since collisions make forces

generate motion. It is made up the three sequential

stages that will be presented in the following

subsections. Roughly speaking, rigid body

simulation can be considered as a large catalogue of

subroutines, some of those are carefully chosen to

fill each of these stages to build systems that

efficiently solve the specific scenes they drive. Here

we show how some of these subroutines can be

implemented on GPU, analyzing pros and cons with

respect to other approaches. Since the subroutines

can be independently incorporated into the whole

simulator, they are interchangeable parts; therefore

systems alternating CPU- and GPU-computations

are available. Nevertheless such hybrid simulators

would require additional tasks to change the

processor (e.g. transmitting data between CPU and

GPU, binding textures to shaders, and assigning

values to uniform variables) that could slow down

the simulation. Thus we will only consider fully

GPU-implementations in the sequel.

A FULLY GPU-IMPLEMENTED RIGID BODY SIMULATOR

343

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

MtF

tdY

)(

Figure 1: Configuration of the state of an object and its.

The programming of GPUs includes stream

processing which is based on the definition of

kernels and streams. Kernels process data in parallel,

while streams organize the information in the

memory card. In our GPU-implementations we use

the following three textures of size

x1 –where 2

is the chosen number of objects; we use power-of-

two sizes since they are required for the algorithm of

Section 2.2– to store the state of any object:

 Linear: a RGBA-texture to store

x(t) and

v(t)

 Rotational: a RGBA-texture to store

r(t) and

ω(t)

 Geometry: a RGBA-texture to store the

geometry of any object as follows: component

R holds the index of the first vertex of the

object, component G is the number of its

vertices, component B keeps its mass, and

component A stores its moment of inertia.

The dynamics of an object is updated after every

simulation step, so the two first textures act as input

and output at the same time, thus we use the ping-

pong technique described in (Gödekke, 2005). Note

that although only two components of the Rotational

texture are required, the format RGBA has been

chosen to allow the renderization to it. The

Geometry texture can be seen as globally-shared

read-only memory that always acts as input. It is

used to determine the current coordinates of the

vertices of the objects, which will be used in the

following stages. We use the first two components

of its texels to access the real coordinates of the

vertices, which will be in a fourth texture called

Vertices. This one can also be seen as globally-

shared read-only memory to keep the –locally

expressed– coordinates. In a 2D scenario, the format

RGBA stores the coordinates of two vertices in each

texel, so the size can be reduced to

Σ{⎡vertex

/2⎤

/ 0≤i≤2

-1}. The following is a fragment of the

GLSL-code to access the vertices of an object. This

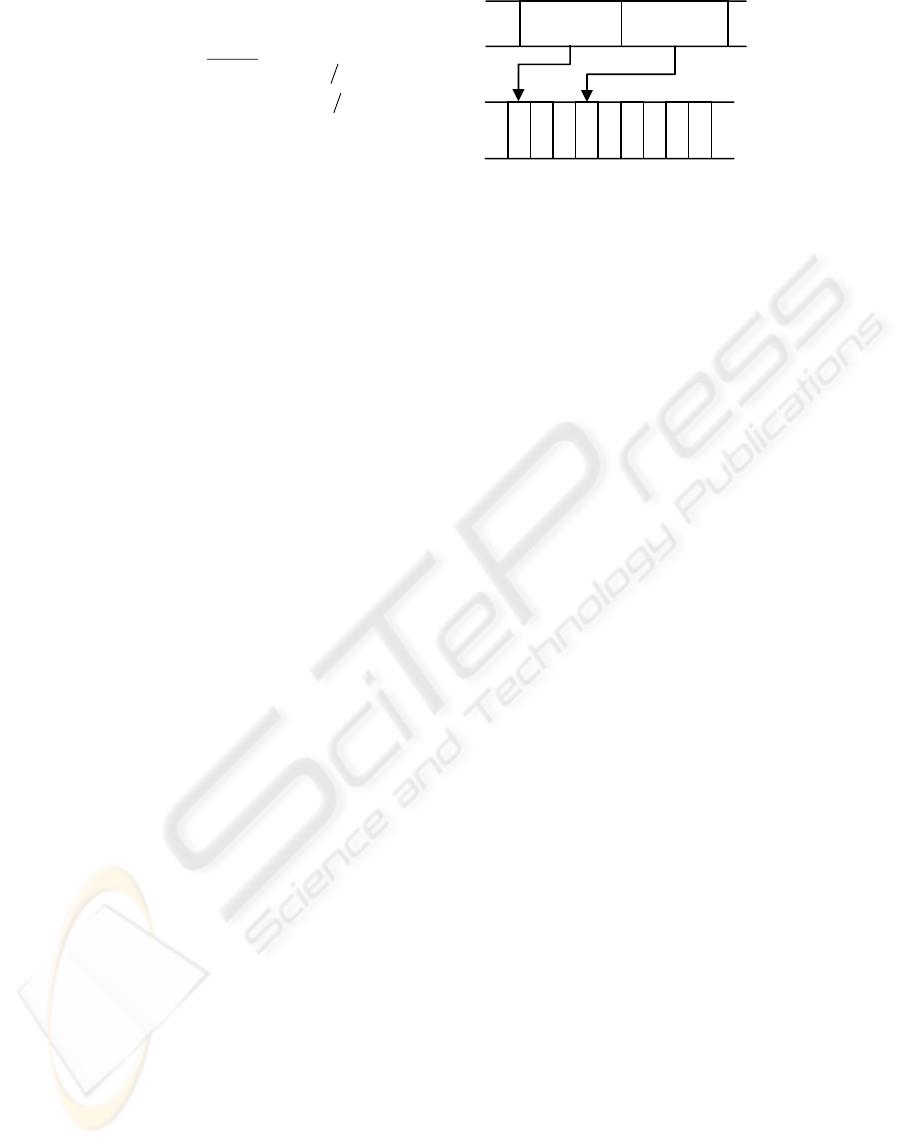
is graphically shown in Figure 2.

//We extract the geometry data of objectI

vec4 geo=textureRect(Geometry,vec2(objectI,0.5));

//The x-component of geo is the address of

//the first vertex of objectI in Vertices

float index=geo.x+0.5;

//We extract the first two vertices of objectI

vec2 v1=textureRect(Vertices,vec2(index,0.5)).xy;

vec2 v2=textureRect(Vertices,vec2(index,0.5)).zw;

In order to focus on the GPU-implementation issues,

we have chosen a 2D rather than a 3D scenario.

Extending the algorithms we propose to the 3D case

is a technical exercise, not covered by this paper. In

this case, most of the data we manage would become

larger, so additional textures would be required. For

example,

x(t) and v(t) should be stored in

separated textures, since they are 3D vectors.

Angular data as

ω(t) and τ(t) also become 3D

vectors, while

r(t) and I should be implemented

through quaternions and 3×3 matrices, respectively.

2.1 Detecting Collisions

In the collision detection stage, the simulator looks

for contacts between pairs of objects. The realism of

the simulation strongly relies on the accuracy in the

detection and computation of these collisions. In

order to minimize the computational effort to detect

collisions, each object is wrapped with an axis

aligned bounding box (AABB). The premise that

motivates its use is the fact that intersections among

AABBs are much easier to detect than the collisions

between the actual objects.

In the simulation loop, prior to compute AABBs

intersections, each volume must be updated

depending on the current position of the contained

object. There are two ways to envelop the object

within a new AABB: either by using the vertices of

the updated object or by using the vertices of the

updated AABB. We have chosen the first method,

which has an updating cost obviously greater than

the second one, but more no-collision situations are

discarded since the volume is tighter to its object.

In order to update bounding volumes, we require

one pass of the kernel

UpdateAABB which renders

Geometry

22, 6, 2, 5 25, 10, 2, 5

25 22

Vertices

Figure 2: Accessing the vertices of an object.

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

344

to a RGBA-texture of size

x1 to encode the

updated AABB related to any object. More

precisely, RG and BA are used for its left-bottom

and right-top corner, respectively. Each fragment

processing includes reading both the current position

and rotation of the object as well as mapping these

transformations to all of its vertices to build the

AABB. Thus, its inputs are the Linear, Rotational,

Geometry and Vertices textures. The cost of

fragment processing depends on the number of

vertices of the related object; hence the whole pass is

a linear operation w.r.t. the total number of vertices.

Once the AABBs have been updated, we check

for overlapping by using one pass of the kernel

OverlapAABB. Its input is the output of the previous

kernel. It renders to a Luminance texture of size

, where the texel (i,j) indicates whether the

AABBs of objects

i and j get to be overlapped.

Now, the cost of a fragment processing is constant,

since only one comparison of the involved corners is

required. Moreover the symmetry of the texture can

be used to restrict the computation to the lower

triangular (LT) region below its main diagonal.

The next phase consists in determining if the

objects contained in the overlapping AABBs

actually collide. We detect such collisions, and the

related collision times, on GPU. In the case of

convex polygons, specific algorithms have been

designed to check whether two objects collide. We

think the classic approach based on separating

planes is not convenient for a GPU implementation,

since they seem rather difficult to be reused in the

simulation. Instead we use a simple algorithm which

behaves well in almost every situation; we do not

consider the remaining ones to be a problem since

the paper does not focus on the simulation realism,

but on comparing GPU- to CPU-implementations.

We actually test if every vertex of a given polygon is

inside the other one. This naive algorithm could be

improved by using the O’Rourke’s approach

(O’Rourke, 1993).

For every pair of objects that will collide after a

complete step, we use the method of bisection to

calculate the exact collision time by testing whether

the objects collide each other in the middle of the

current interval of time. Since the first iteration of

this loop requires the texture produced by

OverlapAABB, the bisection method has been

divided into two kernels:

Bisection1 and

Bisection2. Nevertheless, the two kernels are

essentially the same. They share the Linear,

Rotational, Geometry and Vertices textures as

inputs, and they render to a RGBA-texture

HitTimes of size

, where each texel stores four

data corresponding to the involved pair of objects:

the bounds of the interval enclosing the collision, a

flag to continue (0) or to reject (1) the search of

collision, and the hit time. In order to integrate the

loop related to

Bisection2 we have implemented

two while-sentences. The first one occurs inside the

shader and it is used to calculate the hit time. In

order to prevent from the execution of too many

iterations, we use an extra parameter -a uniform

variable

iter- to control the number of iterations,

since the number of instructions available on the

card is limited. The second one is outside the shader

and it is used to execute the kernel several times.

Due to this multi-pass approach, we successively use

outputs as next inputs. Programming this way allows

us to compare different combinations. The following

is a fragment of the GLSL-pseudo-code of the

Bisection kernels. The uniform variable epsilon

is the accuracy when determining the hit time.

uniform samplerRect Linear, Rotational,

Geometry, Vertices, HitTimes;

uniform float epsilon;

uniform int iter;

vec4 Bisection(float coordObject1, float

coordObject2, float maxTime, float minTime){

//[minTime,maxTime] is the current interval

float maxT=maxTime; float minT=minTime;

vec4 result;

int i=0;

while((maxT-minT>epsilon) && (i<iter)){

float midT=(maxT+minT)/2.0;

if (collision in midT) maxT=midT;

else minT=midT;

i++;

}

if (maxT-minT<=epsilon)

result=vec4(minT,maxT,1,minT);//bisection ends

else result=vec4(minT,maxT,0,minT);//[minT,maxT]

//is the interval for the next bisection pass

return result;

} //Bisection

Table 1 shows timing data for two cases. In the

column Inside (

iter=ceil(-log2(epsilon))),

every iteration takes place inside the shader, while in

the column Outside (

iter=1) only one takes place

inside the kernel. As we see, executing the loop

inside the shader is much better than a pure multi-

pass approach. Along this paper, we have tested the

GPU implementations on a NVIDIA GeForce 7900

GS card. All timing data will be always expressed in

seconds along the paper.

A FULLY GPU-IMPLEMENTED RIGID BODY SIMULATOR

345

Figure 3: a) Darkest texels are not visited when the classic minimization method is applied to the LT region. b) 6-reduction.

c) (4+6)-reduction. In b) and c), darkest texels are visited more than once.

Table 1: Running 1000 times the Bisection kernels for the

two forms of iterating. An initial random scene has been

used in each row.

At the end of the two kernels we have a texture

of size

, with the alpha component containing

the hit time t∈[0,1] for every pair of objects, or a

constant greater than 1 to indicate that the related

objects do not collide. Due to symmetry, the kernel

only requires to process the LT region of the texture.

2.2 Searching the First Collision

There are different ways to process the contacts

computed in the previous phase. On one hand, we

can arrange the contacts with respect to the collision

time. The problem is that solving one collision may

affect many other collisions produced later within

the same step. To be precise, some of them could not

be produced or even new collisions could arise. On

the other hand, there is a simpler approach

consisting in truncating the step at the just moment

of the first contact, and discarding the rest. We have

chosen this latter approach; so we have used the

classic reduction kernel (Buck and Purcell, 2004) to

compute the minimum of the collision times.

Nevertheless, we have proposed and analyzed

different methods to improve the classic reduction

kernel by exploiting the symmetry of the input

textures. For all of them, the input is a texture of size

, where the texel (i,j) stores the floating

point corresponding to the collision time of the

objects

i and j, or a constant greater than 1 if they

do not collide. Since the texture is symmetric and its

main diagonal is irrelevant, we can restrict to texels

with

i<j. The output of the kernel will be computed

by successively iterating a shader to halve each

texture dimension.

In the classic method, the fragment processing

computes the minimum of a

2×2 square. Since the

texture is symmetric, our approach only requires

Table 2: Comparing the three reduction methods for 1000

complete minimizations.

processing the LT region. If we applied the classic

2×2 reduction to the LT region, some texels would

not be considered (Figure 3a). In order to include

them, we must visit six texels when processing

fragment

(i,j), those with coordinates (2i,2j),

(2i+1,2j), (2i,2j+1), (2i+1,2j+1), (2i-

1,2j) and (2i+1,2j+2). This solution, which we

call 6-reduction, improves the classic algorithm, but

it generates too many redundant readings (Figure

3b). In order to avoid them, we exploit the fact that

only the adjacent components to the diagonal need

to check the six elements, while the others only

require the four elements of the classic method.

Therefore this (4+6)-reduction is a combination of

two shaders: one to check the six elements that

correspond to fragments adjacent to the diagonal,

and the other one to check the four elements that

correspond to the remaining fragments of the LT

region (Figure 3c).

The complexity of a pass reducing a texture of

size

2m×2m to a texture of size m×m is 4m

for the

classic algorithm,

3(m

-m) for the 6-reduction and

2(m

-1) for the (4+6)-reduction, with respect to the

number of required readings. Since the complete

reduction process is based on a multi-pass approach,

the quadratic coefficient involved in a single pass

becomes critical. Table 2 compares the three

options, running 1000 complete minimizations. As it

was expected, results report that the (4+6)-reduction

significantly reduces time as the texture size

increases.

2.3 Solving the First Collision

After computing the minimum hit time, we must

apply the related response on the GPU. Firstly, we

Inside Outside

0.6100 1.1500

0.7200 1.7875

0.7600 10.200

1.1400 10.600

Classic 6-reduction (4+6)-reduction

1.422 1.625 1.532

1.750 1.906 1.438

2.031 2.047 1.656

3.187 2.437 1.831

14.265 10.939 6.484

)

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

346

check whether the contacts at the same time are real

collisions. The relative velocity

rel

of the pair of

objects A and B is useful to solve this question:

( ..)()( (..)1)

rel hit hit hit

dp dp

Vttnt

dt dt

⎛⎞

=−⋅

⎜⎟

⎝⎠

where

dp/dt denotes the velocity of the contact

point within the corresponding object, and

n is the

contact normal. If V

rel

<0 (see Figure 4), the objects

are colliding and an impulse must be computed to

avoid that they get overlapped. The impulse

J is an

instantaneous force, thus it produces a variation of

the velocities according to the following equations:

Δv=J/M and Δω =Γ

/I, where the torque is defined

by Γ

=(p-x(t))×J. The impulse J is a vector

whose direction is the contact normal n and whose

magnitude

j must be computed by using the

following equation (2):

(1 )

() ()

rel

AB A B

rnt rnt

nt r nt r

MM I I

−

−+

⎛⎞ ⎛⎞

××

++ ×+ ×

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

where

ε is the restitution coefficient between the two

objects,

rel

−

is the relative velocity before the

impulse, and

, r

are the vectors from the center of

mass of each object to the contact point p. The

action of

J is positive (+jn(t)) on the object A and

negative (

-jn(t)) on B.

The computation of the impulse is carried out by

the kernel

Impulse. Its inputs are the Linear,

Rotational, Geometry, Vertices and HitTimes

textures, and the minimum hit time. It renders to a

RGBA-texture of size

, where the texel (i,j)

stores the accumulation of the impulses between the

objects

i and j, since several collisions points can

simultaneously arise. The impulse is computed

whenever the collision time equals the minimum hit

time. If this is the case, the accumulation of impulses

is performed as the following pseudo-code shows.

while (i<numVerticesA) {

while (j<numEdgesB) {

if (i-th vertex of A is on the j-th edge of B){

1.- Compute Vrel of A and B in the i-th

vertex of A

2.- If (Vrel<0) {

2.1.- Compute the impulse

2.2.- Accumulate the impulse

}}}}

//Repeat with vertices of B and edges of A

Finally we execute one pass of any of the

following kernels to update the scene after a step of

the simulation:

NoCollisionForward and

CollisionForward. Their inputs and outputs are

the Linear and Rotational textures. The kernel

NoCollisionForward is used when the instant of

the first collision is greater than a step of time. In

this case, no collision is produced, the impulse is not

computed, and the kernel updates the objects until

the end of the step of time. Thus, processing a

fragment requires constant time. The kernel

CollisionForward is used otherwise and includes

the output texture of the kernel

Impulse as input.

This kernel accumulates the impulses between an

object and the remaining objects, and applies the

total impulse. Hence processing a fragment requires

linear time.

3 THE RENDERING PHASE

The image of the objects after a step is obtained by a

vertex shader, which applies the transformations

needed to suitably translate and rotate the object in

the scene. This entails two jobs.

First of all, the translation and the rotation of the

processed object must be loaded. Since the Linear

and Rotational textures are located in memory card,

they must be read back from GPU to CPU after any

step. This option is called toCPU in Table 3. On the

other hand, we can access these data within the

shader itself by using a uniform variable to hold the

texture coordinates that must be read. We use such a

variable as an index, which must be properly

assigned before rendering the object. This option is

called Index in Table 3. The total cost of the latter

approach includes two texture accesses per vertex,

plus an extra uniform assignment per object.

rel

> 0

rel

= 0

rel

< 0

Figure 4: Relative velocity

(

)()( t

rel

−=

) of objects A and B.

A FULLY GPU-IMPLEMENTED RIGID BODY SIMULATOR

347

Second, the shader needs the local coordinates of

every vertex. Now we must decide how to send

vertices to the pipeline. We propose these options:

1. Sending fictitious coordinates that will be

replaced with the coordinates stored in the

Vertices texture. In order to access the

Geometry and Vertices textures, the shader

needs the index of the object and the ordinal of

the vertex within the object. To this aim, the

simplest way is to use the fictitious coordinates

to communicate these data to the shader. More

precisely, the

x-coordinate indicates the object

and the

y-coordinate refers to the vertex offset

when accessing the Vertices texture. Hence any

fragment processing requires two texture

accesses: one to read the object data in the

Geometry texture, and another to get the local

coordinates of the vertex in the Vertices texture.

2. Sending fictitious coordinates and using one of

them to indicate the ordinal of the vertex within

the object, as in the previous option, and the

other one to refer to the location of the first

vertex of the object within the Vertices texture.

Thus, we save one access per vertex.

3. Directly sending the local coordinates of each

vertex to save the two accesses. The

disadvantage of this option is that a copy of the

Vertices texture must be located in CPU

memory.

Table 3 compares the six combinations related to the

solutions of the two jobs, that is, the two options to

read the transformations and the three options to

send the coordinates to the pipeline. The time

measures correspond to 1000 renderings of a random

scene configuration. In the last row we show how

many texture accesses (a) are required per vertex,

how many uniforms (u) must be assigned per object,

and how many textures (t) have to be read from

GPU to CPU. Note that texture accesses from vertex

shaders are only available from shader model 3.0.

Table 3: Comparing the six implementations of the

rendering phase.

4 CASE STUDIES

We have implemented two versions of the previous

simulation algorithms, including different geometric

shapes: the first for circles and the second for

convex polygons. Our shaders need several GPU

capabilities supported from the shader model 3.0,

such as texture accesses from a vertex shader, or

conditions in loops that cannot be solved at compile

time. The time measures correspond to 1000 steps in

order to reduce measurement errors. Apart from the

GPU implementation, we have also developed a

CPU version of every algorithm. They have been run

on an Intel Core 2 Duo 1,86 Ghz. A comparison is

shown in Table 4. The initial scene is randomly

generated. In addition, initial positions are enclosed

within a squared room to improve the simulation

visualization. Walls are differently implemented in

each case.

4.1 Circles

Circles are the simplest shapes in rigid body

simulation, mainly because rotations can be skipped.

It is also possible to compute the hit time of two

circles algebraically, thus the bisection loop can be

changed into a constant time code. It is enough to

solve the equation

distance(A+ta,B+tb)=r

where r

, r

are the radius, A, B are the centres, and

a, b are the linear velocities of the two circles. It

leads to a second order equation which must be

solved to find the, at the most, two values of

Nevertheless the difference between both

approaches is irrelevant since the few but expensive

computations of the algebraic approach can be

compared to the low-cost but many iterations of the

bisection loop. Table 4 compares both approaches.

The walls are also easy to implement since perfect

reflections are applied.

4.2 Convex Polygons

For the sake of convenience, we only generate

scenes with regular polygons. In fact we only use

triangles in Table 4. The bisection kernels are

required to compute hit times. Walls are

implemented as rectangular objects with infinite

mass, so they are static objects. Table 4 shows that

the GPU implementation significantly reduces time

as the number of objects increases.

Option 1 Option 2 Option 3

Index toCPU Index toCPU Index toCPU

16.659

16.649

16.659

25.909

26.239

25.870

23.969

16.670

16.659

51.580

49.110

50.910

45.639

33.330

16.659

117.26

102.27

102.37

89.750

65.529

16.659

2a+2t+2

3a+1u

1a+2t+2

2a+1u 2t+2u

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

348

Table 4: Comparing the three circles implementations

(GPU-algebraic, GPU-bisection, CPU-bisection) and the

two polygons ones (GPU-bisection, CPU-bisection).

Table 5 shows the timing data of the main

kernels of the simulation algorithm after running

1000 steps on the same initial random configuration.

Hence we cannot use it to deduce which kernel is the

most demanding one, since their execution depends

on the initial configuration. For instance, the

Bisection2 kernel will not run whenever the

OverlapAABB kernel computed no pair of

overlapping AABBs, and the

Impulse and the

CollisionForward kernels do not run whenever

no collision arises.

Table 5: Timing data of the kernels used in the simulation.

Finally, we show in Figure 5 a snapshot of the

rigid body simulator applied to a scene made up of

1024 dynamic triangles, with a detail of the scene

highlighted.

Figure 5: Snapshot of the rigid body simulator.

5 CONCLUSIONS

In this paper we have presented a fully GPU-

implemented rigid body simulator, which is suitably

composed of different −fragment and vertex−

shaders to execute both the simulation and the

renderization tasks. Moreover we have proposed

several solutions for many of the development

phases, comparing their behavior. Finally, we have

applied these techniques to two case studies, one

based on circles and another on convex polygons.

The main contribution of the paper is to show

that the GPU capabilities can be used to improve the

overall timing of a CPU implementation. In the case

studies, we compare our GPU solutions to analogous

CPU versions, showing that GPU implementations

win as the number of objects increases.

REFERENCES

Baraff, D., 1989. Analytical Methods for Dynamic

Simulation of Non-Penetrating Rigid Bodies. In

SIGGRAPH’89, 223-232.

Baraff, D., 1997. Rigid Body Simulation. An Introduction

to Physically Based Modeling. In SIGGRAPH’97,

course notes.

Buck, I., Purcell, T., 2004. A Toolkit for Computation on

GPUs. In GPU Gems, Addison-Wesley, 621-636.

Göddeke, D., 2005. GPGPU: Basic Math Tutorial. TR.

300, Fachbereich Mathematik, Universität Dortmund.

Govindaraju, N., Lin, M., Manocha, D., 2005. Quick-

CULLIDE: Fast Inter- and Intra-Object Collision

Culling Using Graphics Hardware. In IEEE Virtual

Reality Conference, 59-66, 319.

Greß, A., Guthe, M., Klein, R., 2006. GPU-based

Collision Detection for Deformable Parameterized

Surfaces. In Computer Graphics Forum 25(3), 497-506.

Greß, A., Zachmann, G., 2004. Object-Space Interference

Detection on Programmable Graphics Hardware. In

Geometric Modeling and Computation. Proc. of

SIAM Conference on Geometric Design and

Computing, 311-328.

Gu, X., Gortler, S., Hoppe, H., 2002. Geometry Images. In

ACM Trans. Graph 21(3), 355-361.

Horn, D., 2005. Stream reduction operations for GPGPU

applications. In GPU Gems 2, Addison-Wesley, 573-

589.

Kim, J., Kim, S., Ko, H., Terzopoulos, D., 2006. Fast GPU

Computation of the Mass Properties of a General

Shape and its Application to Bouyancy Simulation. In

Int. Journal of Computer Graphics 22(9), 856-864.

Krüger, J., Kipfer, P., Kondratieva, P., Westermann, R.,

2005. A Particle System for Interactive Visualization

of 3D Flows. In IEEE Transactions on Visualization

and Computer Graphics 11(6), 744-756.

Circles Polygons

GPU-alg GPU-bis CPU-bis GPU-bis CPU-bis

33.62 33.56 33.33 17.47 16.66

50.16 50.16 86.14 17.50 36.27

83.49 83.47 356.42 26.83 192.63

166.79 166.89 1603.10 67.62 810

Update Overlap Bisection Impulse Forward

0.1599 0.2500 0.6100 0.3200 0.0390

0.1700 0.6869 0.7200 0.3200 0.0799

0.1899 2.4700 0.7600 0.3600 0.2100

0.2300 9.4600 1.1400 0.5200 0.2300

A FULLY GPU-IMPLEMENTED RIGID BODY SIMULATOR

349

McKenna, M., Zeltzer, D., 1990. Dynamic Simulation of

Autonomous Legged Locomotion. In Computer

Graphics 24(4), 29-38.

Mirtich, B., 1996. Impulse-Based Dynamic Simulation of

Rigid Body Systems. Ph. D. dissertation. University of

California, Berkeley, CA.

Mirtich, B., 2000. Timewarp Rigid Body Simulation. In

SIGGRAPH‘00, 193-200.

O’Rourke, J., 1993. Computational Geometry in C,

Cambridge University Press.

Pascale, M., Sarcuni, G., Prattichizzo, D., 2005. Real-

Time Soft-Finger Grasping of Physically Based Quasi-

Rigid Objects. In World Haptic Conference, 545-546.

Raabe, A., Hochgürtel, S., Anlauf, J., Zachmann, G.,

2006. Hardware-Accelerated Collision Detection using

Bounded-Error Fixed-Point Arithmetic. In Journal of

WSCG 14, 17-24.

Teschner, M., Kimmerle, S., Heidelberger, B., Zachmman,

G., Raghupathi, L., Furmann, A., Cani, M., Faure, F.,

Magnenat-Thalmann, N., Strasser, W., Volino, P.,

2005. Collision detection for deformable objects. In

Computer Graphics Forum 24(1), 61-81.

Yuksel, C., 2007. Real-Time Impulse-Based Rigid Body

Simulation and Rendering. Master Thesis, Texas

A&M University.

Zhang, X., Kim, Y. J., 2007. Interactive Collision

Detection for Deformable Models using Streaming

AABBs. In IEEE Trans. on Visualization and

Computer Graphics 13(2), 318-329.

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

350