GPC AND NEURAL GENERALIZED PREDICTIVE CONTROL
S. Chidrawar
1
Nikhil Bidwai
2
, L. Waghmare
2
and B. M. Patre
2
1
MGM’s College of Engineering, Nanded (MS) 431 602, India
2
SGGS Institute of Engineering and Technology, Nanded (MS) 431 606, India
Keyword: Neural network, Model predictive control, GPC, NGPC.
Abstract: An efficient implementation of Model Predictive Control (MPC) using a multilayer feed forward network as
the plants linear model is presented. This paper presents a comparison between the Generalized Predictive
Control and Neural Generalized Predictive Control with Newton-Raphson as minimization algorithm. Three
different linear models are taken and their performances are tested. Simulation result shows the effect of
neural network on Generalized Predictive Control for linear systems. The performance comparison of these
system configurations has been given in terms of ISE and IAE.
1 INTRODUCTION
Model predictive control (MPC) has found a wide
range of applications in the process, chemical, food
processing, automotive, aerospace, metallurgy, and
pulp and paper industries. (Qin and Badgwell, 2003;
Yu, Yu and Gomm, 2006; Lawrynczuk, 2007). In
recent years, the requirements for the quality of
automatic control in the process industries increased
significantly due to the increased complexity of the
plants and sharper specifications of product quality.
As a result, computer models that are
computationally expensive became applicable even
to rather complex problems. Intelligent and model
based control techniques were developed to obtain
tighter control for such applications. Neural network
techniques has been found to be particularly useful
for modeling and controlling highly uncertain
nonlinear and complex systems. (Noorgard, Ravn,
Poulsen and Hansen, 2000). The Model Predictive
Control (MPC) techniques found to be very effective
in control systems. MPC was introduced
successfully in several industrial plants. Some of the
most popular MPC algorithms that found a wide
acceptance in industry are Dynamic Matrix Control
(DMC), Model Algorithmic Control (MAC),
Predictive Functional Control (PFC), Extended
Prediction Self Adaptive Control (EPSAC),
Extended Horizon Adaptive Control (EHAC) and
Generalized Predictive Control (GPC). (Morari and
Lee, 1999, Rossiter, 2003). In this work, comparison
between GPC and Neural GPC has been carried out
for linear systems. The results show the efficacy of
NGPC for such plants.
2 GENERALIZED PREDICTIVE
CONTROL
The GPC method was proposed by Clarke et. al.
(Clarke, Mohatadi and Tuffs, 1987) and has become
one of the most popular MPC methods both in
industry and academia.
The basic idea of GPC is to calculate a sequence
of future control signals in such a way that it
minimizes a multistage cost function defined over a
prediction horizon. The index to be optimized is the
expectation of a quadratic function measuring the
distance between the predicted system output and
some reference sequence over the horizon plus a
quadratic function measuring the control effort. The
GPC scheme consists of the plant to be controlled, a
reference model that specifies the desired
performance of the plant, a linear model of the plant,
and the Cost Function Minimization (CFM)
algorithm that determines the input needed to
produce the plant’s desired performance. The GPC
system starts with the input signal, r(t), which is
presented to the reference model. This model
produces a tracking reference signal, w (t) that is
used as an input to the CFM block. The CFM
algorithm produces an output, which is used as an
input to the plant. Between samples, the CFM
266
Chidrawar S., Bidwai N., Waghmare L. and M. Patre B. (2008).
GPC AND NEURAL GENERALIZED PREDICTIVE CONTROL.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 266-270
DOI: 10.5220/0001476102660270
Copyright
c
 SciTePress

algorithm uses this model to calculate the next
control input, u(t+1), from predictions of the
response from the plant’s model. Once the cost
function is minimized, this input is passed to the
plant.
3 NEURAL GENERALIZED
PREDICTIVE CONTROL
The ability of the GPC to make accurate predictions
can be enhanced if a neural network is used to learn
the dynamics of the plant instead of standard
nonlinear modeling techniques.(Noorgard, Ravn,
Poulsen and Hansen, 2000). The selection of the
minimization algorithm affects the computational
efficiency of the algorithm. In this work Newton-
Raphson method is used as the optimization
algorithm. The main cost of the Newton-Raphson
algorithm is in the calculation of the Hessian, but
even with this overhead the low iteration numbers
make Newton-Raphson a faster algorithm for real-
time control. (Soloway, 1996). The Neural
Generalized Predictive Control (NGPC) system can
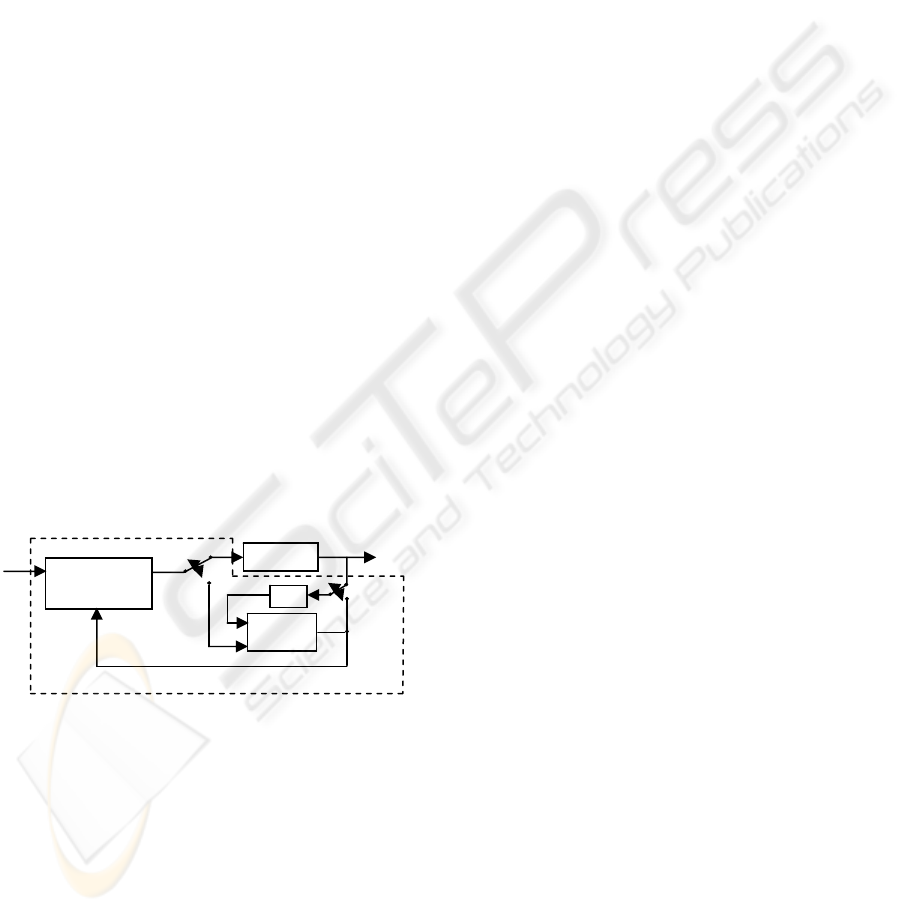
be seen in Fig. 1. It consists of four components, the
plant to be controlled, a reference model that
specifies the desired performance of the plant, a
neural network that models the plant, and the Cost
Function Minimization (CFM) algorithm that
determines the input needed to produce the plant’s
desired performance. The NGPC algorithm consists
of the CFM block and the neural net block.
Figure 1: Block Diagram of NGPC System.
The NGPC system starts with the input signal, r(t),
which is presented to the reference model. This
model produces a tracking reference signal, w(t+k),
that is used as an input to the CFM block. The CFM
algorithm produces an output that is either used as
an input to the plant or the plant’s model. The
double pole double throw switch, S, is set to the
plant when the CFM algorithm has solved for the
best input, u(t), that will minimize a specified cost
function. Between samples, the switch is set to the
plant’s model where the CFM algorithm uses this
model to calculate the next control input, u(t+1),
from predictions of the response from the plant’s
model. Once the cost function is minimized, this
input is passed to the plant. The computational
performance of a GPC implementation is largely
based on the minimization algorithm chosen for the
CFM block. Models using neural networks have
been shown to have the capability to capture
nonlinear dynamics. Improved predictions affect rise
time, over-shoot, and the energy content of the
control signal.
3.1 Formulation of NGPC
3.1.1 Cost Function
As mentioned earlier, the NGPC algorithm
(Soloway, 1996) is based on minimizing a cost
function over a finite prediction horizon. The cost
function of interest to this application is
[][]
2
22
ˆ
(, , ) ()( |) ( ) () ( 1)
12
1
1
N
N
u
JNNN jytjt wtj j utj
u
jN j
δλ =+−++Δ+−
∑∑
==
(1)
N
1
= Minimum Costing Prediction Horizon
N
2
= Maximum Costing Prediction Horizon
N
u
= Length of Control Horizon
()yt kt
∧
+
⏐
= Predicted Output from Neural;
Network,
()ut kt
+⏐
= Manipulated Input
()wt k
+
= Reference Trajectory
δ and λ = Weighing Factor
When this cost function is minimized, a control
input that meets the constraints is generated that
allows the plant to track the reference trajectory
within some tolerance. There are four tuning
parameters in the cost function, N
1
, N
2
, N
u
, and λ.
The predictions of the plant will run from N
1
to N
2
future time steps. The bound on the control horizon
is N
u
. The only constraint on the values of N
u
and N
1
is that these bounds must be less than or equal to N
2
.
The second summation contains a weighting factor,
λ that is introduced to control the balance between
the first two summations. The weighting factor acts
as a damper on the predicted u(n+1).
3.1.2 Cost Function Minimization Algorithm
The objective of the CFM algorithm is to minimize J
in Equation (1) with respect to [u(n+l), u(n+2), ...,
u(n+N
u
)]
T
, denoted as U. This is accomplished by
setting the Jacobian of Equation (1) to zero and
solving for U. With Newton-Rhapson used as the
CFM algorithm, J is minimized iteratively to
Cost Function
Minimization
(CFM)
Plant
Neural
Plant Model
z
-1
y(t)
()
n
yt kt
∧
+⏐
()wt k+
u(t)
s
s
NGPC Algorithm
GPC AND NEURAL GENERALIZED PREDICTIVE CONTROL
267

determine the best U. An iterative process yields
intermediate values for J denoted J(k). For each
iteration of J(k) an intermediate control input vector
is also generated and is denoted as:
(1)
(2)
.
()
.
.
()
u
ut
ut
Uk
ut N
Δ
+
⎡⎤
⎢⎥
+
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎢⎥
+
⎢⎥
⎣⎦
k=1,....N
u
(2)
Using this Newton-Raphson update rule,
(1)Uk
+
is
1
2
2
(1) () () ()'
JJ
Uk Uk k k
UU
−
⎛⎞
∂∂
+= −
⎜⎟
∂∂
⎝⎠
where
()
J
fx
U
∂
=
∂
(3)
where the Jacobian is denoted as
(1)
.
.
()
.
()
u
J
ut
J
k
U
J
ut N
∂
⎡⎤
⎢⎥
∂+
⎢⎥
⎢⎥
∂
⎢⎥
≡
⎢⎥
∂
⎢⎥
⎢⎥
∂
⎢⎥
⎢⎥
∂+
⎣⎦
(4)
and the Hessian as
22
2
2
2
22
2
..
(1) (1)( )
....
() .
....
..
()(1) ()
u
uk u
JJ
ut ut ut N
J
k
U
JJ
ut N u t ut N
⎡⎤
∂∂
⎢⎥
∂+ ∂+∂+
⎢⎥
⎢⎥
∂
≡
⎢⎥
∂
⎢⎥
⎢⎥
∂∂
⎢⎥
∂+ ∂ + ∂+
⎢⎥
⎣⎦
(5)
The each element of the Jacobian is calculated by
partially differentiating (4) with respect to vector U.
3.1.3 Neural Network Architecture
In NGPC the model of the plant is a neural network.
This neural model is constructed and trained using
MATLAB Neural Network System Identification
Toolbox commands and Control System Design
Toolkit (Noorgard, Ravn, Poulsen and Hansen,
2000).
The output of trained neural network is used as
the predicted output of the plant. This predicted
output is used in the Cost Function Minimization
Algorithm. If y
n
(t) is the neural network’s output
then it is nothing but plant’s predicted output
()
n
yt kt
∧
+
⏐
.
The initial training of the neural network is typically
done off-line before control is attempted
3.1.4 Prediction using Neural Network
The NGPC algorithm uses the output of the plant's
model to predict the plant's dynamics to an arbitrary
input from the current time, t, to some future time,
t+k.
4 SIMULATION RESULTS
The objective of this study is to show how GPC and
NGPC implementation can cope with linear systems.
GPC is applied to the systems with changes in
system order. The Neural based GPC is
implemented using MATLAB Neural Network
Based System Design Toolbox (Noorgard, Ravn,
Poulsen and Hansen, 2000).
4.1 GPC and NGPC for Linear
Systems
The GPC and NGPC algorithm was applied to the
different linear models with varying system for
simulation purpose. For all the systems Prediction
Horizon N
1
=1, N
2
=7 and Control Horizon (N
u
) is 2
have been considered. The weighing factor λ for
control signal is kept to 0.3 and δ for reference
trajectory is set to 0. The same controller setting is
used for all the systems simulation. The following
simulation results are obtained showing the plant
output when GPC and NGPC are applied. Also the
required control action for different systems is
shown.
System I. The GPC and NGPC algorithms are
applied to a second order system (6). Fig. 2 shows
the plant output with GPC and NGPC. Fig. 3 shows
the control efforts taken by both controllers.
2
1
()
110 40
Gs
s
s
=
++
(6)
Figure 2: System I Output using GPC and NGPC.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
268

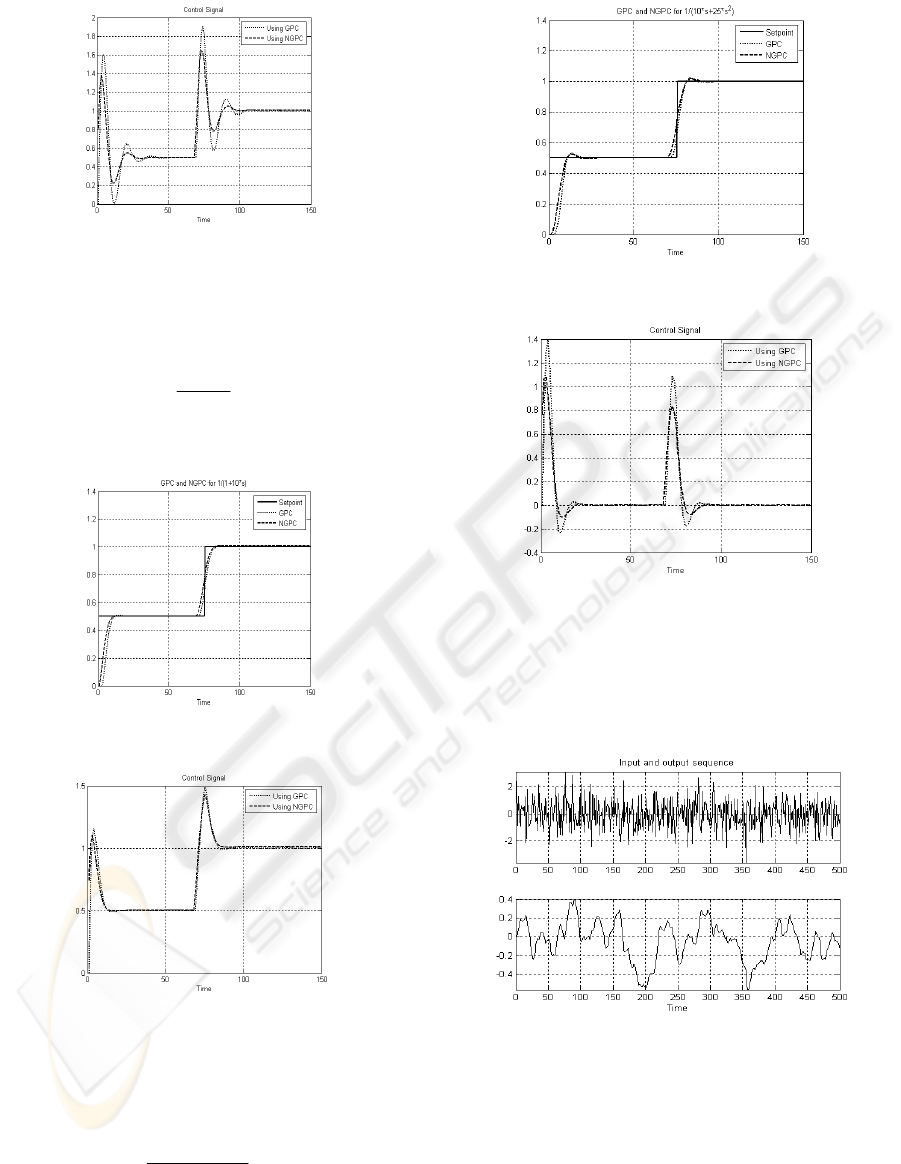
Figure 3: Control Signal for System I.
System II. A simple first order system (7) is
controlled. Fig. 4 and Fig. 5 show the system output
and control signal.
1
()
110
Gs
s
=
+
(7)
Figure 4: System II Output using GPC and NGPC.
Figure 5: Control Signal for System II.
System III. A second order system (8) is controlled
using GPC and NGPC. Fig.6 and Fig.7 Show the
predicted output and control signal.
1
()
10 (1 2.5 )
Gs
s
s
=
+
(8)
Figure 6: System III Output using GPC and NGPC.
Figure 7: Control Signal for System III.
Initially systems were trained using Levenberg-
Marquardt learning algorithm. Fig. 8 shows input
data applied to the neural network for offline
training purpose and corresponding neural network
output.
Figure 8: Input and output data for NN.
Performance evaluation of both the controller is
carried out using ISE and IAE criteria. Table 1 gives
ISE and IAE values for both GPC and NGPC
implementation for all the linear systems considered.
It was observed that for each system ISE and IAE
using NGPC is smaller or equal to GPC.
GPC AND NEURAL GENERALIZED PREDICTIVE CONTROL
269

Table 1: ISE and IAE Performance Comparison of GPC
and NGPC for Linear System.
GPC NGPC Systems Setpoint
ISE IAE ISE IAE
0.5 1.827 4.4107 1.6055 3.6351 I
1 0.2567 1.4492 0.1186 1.4312
0.5 1.1803 3.217 0.7896 2.6894 II
1 0.1311 0.767 0.063 1.017
0.5 1.4639 3.7625 1.1021 3.3424 III
1 0.1759 0.9065 0.0957 0.7062
5 CONCLUSIONS
In this paper a comparison between GPC and NGPC
is carried out for linear systems. The performance of
NGPC is better that GPC in terms of ISE and IAE
Performance index.
REFERENCES
Qin, S. J., Badgwell, T., 2003. A survey of industrial
model predictive control technology. Control
Engineering Practice. Vol. 11. no. 7. pp. 733-764.
Yu, D. L., Yu, D. W., Gomm, J. B., 2006. Neural model
adaptation and predictive control of a chemical rig.
IEEE Transaction on Control Systems Technology.
Vol. 14. no. 5. pp. 828-840.
Lawrynczuk, M., 2007. An efficient nonlinear predictive
control algorithm with neural models based on
multipoint on-line linearization. EUROCON 2007.
The International Conference on “Computer asa Tool.
Warsaw. September 9-12. pp. 777-784
Noorgard, M., Ravn, O., Poulsen, N. K., Hansen, L. K.
2000. Neural networks for modeling and control of
dynamical systems. Springer, London.
Morari, M., Lee, J. 1999. Model predictive control: past,
present and future. Computers and Chemical
Engineering. Vol. 23. no. 4/5. pp. 667- 682
Rossister, J. A. 2003. Model based predictive control.
CRC Press. Boca Raton.
Clarke, D. W., Mohtadi, C., Tuffs, P. S. 1987. Generalized
predictive control- Part I, The basic algorithm.
Automatica. Vol. 23. pp. 137-148.
Soloway, D. 1996. Neural generalized predictive control.
Proceedings of the 1996 IEEE International
Symposium on Intelligent Control. Dearborn,
September, 15-18. pp. 227-282.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
270