SELF-ORGANISATION OF GAIT PATTERN TRANSITION

An Efﬁcient Approach to Implementing Animal Gaits and Gait Transitions

Zhijun Yang, Juan Huo and Alan Murray

Institute of Micro and Nano Systems, School of Engineering and Electronics

Edinburgh University, Edinburgh EH16 6XD, U.K.

Keywords:

Central pattern generator, oscillatory building block, gait transitions, Self-organisation, Hopﬁeld network.

Abstract:

As an engine of almost all life phenomena, the motor information generated by the central nervous system

(CNS) plays a critical role in the activities of all animals. Despite the difﬁculty of being physically identiﬁed,

the central pattern generator (CPG), which is a concrete branch of studies on the CNS, is widely recognised

to be responsible for generating rhythmic patterns. This paper presents a novel, macroscopic and model-

independent approach to the retrieval of different patterns of coupled neural oscillations observed in biological

CPGs during the control of legged locomotion. Based on the simple graph dynamics, various types of oscil-

latory building blocks (OBB) can be reconﬁgured for the production of complicated rhythmic patterns. Our

quadrupedal locomotion experiments show that an OBB-based artiﬁcial CPG model alone can integrate all

gait patterns and undergo self-organised gait transition between different patterns.

1 INTRODUCTION

Animal gait analysis is an ancient science. As early

as two thousand years ago, Aristotle described the

walk of a horse in his treatise (Aristotle, 1936).

In modern biological research, it is widely believed

that animal locomotion is generated and controlled,

in part by central pattern generators (CPG), which

are networks of neurons in the central nervous sys-

tem (CNS) capable of producing the rhythmic out-

puts (Stein, 1978),(Grillner, 1985),(Pearson, 1993).

The constituents of the locomotory motor system are

traditionally modelled by nonlinear coupled oscilla-

tors, representing the activation of ﬂexor and ex-

tensor muscles by, respectively, two neurophysio-

logically simpliﬁed motor neurons (Linkens et al.,

1976),(Tsutsumi and Matsumoto, 1984),(Bay and

Hemami, 1987). Despite its mathematical accuracy

and ability to mimic some basic oscillatory features,

this approach provides, however, neither a sufﬁciently

detailed description of the real biological mechanisms

nor a model simple enough for application purpose.

Based on the graph dynamics, in this paper we present

a structural approach to the modelling of the complex

behavioural dynamics with a new concept of oscilla-

tory building blocks (OBB) (Yang and Franca, 2003),

(Yang and Franca, 2008). For the ﬁrst time we present

that the OBB model is able to self-organise its dif-

ferent gait pattern outputs under the control of a se-

lecting signal ﬂow in the neuro-musculo-skeletal sys-

tem. Through appropriate selection and organisation

of suitably conﬁgured OBB modules, different gait

patterns and transitions between different patterns can

be achieved for producing complicated rhythmic out-

puts, retrieving realistic locomotion prototypes and

facilitating the very large scale integrated (VLSI) cir-

cuit synthesis in an efﬁcient, uniform and systematic

framework.

2 METHOD

Out-of-phase (walking and running) and in-phase

(hopping) are the major characteristics of observed

gaits in bipeds, while in quadrupeds more gait types

were observed and enumerated (Alexander, 1984), as

walk, trot, pace, canter, gallop, bound and pronk. Un-

like bipeds and quadrupeds, hexapod locomotion can

have more complicated combinations of leg move-

ments. Despite the variety, however, some general

symmetry rules should still be obeyed and remained

as the basic criteria for gait prediction and construc-

tion. For instance, it is a generally accepted view that

multi-legged (usually more than six legs) locomotion

often display a travelling wave sweeping along the

chain of oscillators (Collins and Stewart, 1993),(Gol-

Yang Z., Huo J. and Murray A. (2008).

SELF-ORGANISATION OF GAIT PATTERN TRANSITION - An Efﬁcient Approach to Implementing Animal Gaits and Gait Transitions.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 75-79

DOI: 10.5220/0001476400750079

 SciTePress

ubitsky et al., 1998). In order to construct a novel,

uniform OBB-based CPG architecture to integrate all

gaits as well as the self-organised gait transitions of

a speciﬁc legged animal, we need a case study of the

simple graph dynamics as a start.

2.1 A Case of Graph Dynamics

Consider a system consisting of a set of processes and

a set of atomic shared resources represented by a con-

nected graph G = (N,E), where N is the set of pro-

cesses and E the set of edges deﬁning the interconnec-

tion topology. An edge exists between any two nodes

if and only if two corresponding processes share at

least one atomic resource (Fig. 1).

j k

Figure 1: A simple graph dynamics representing an opera-

tion cycle, r

= r

= 2, r

= r

= 1, dark-ﬁlled circle repre-

sents a node is operating.

Between any two nodes i and j, i, j ∈ N, there can

exist e

unidirected edges, e

≥ 0. The reversabil-

ity of node i is r

, i.e., the number of edges that shall

be reversed by i to each of its neighbouring nodes,

indiscriminately, at the end of the operation. Node i

is an r

-sink if it has at least r

edges directed to it-

self from each of its neighbours. Only r

-sink node

can operate and reverse r

edges towards each of its

neighbours, the new set of r

-sinks will operate, and

so on. In order to avoid operation deadlock, the shared

resources between any two nodes, e

, must satisfy

= r

+ r

− gcd(r

), and max{r

} ≤ e

≤

−1 (Barbosa, 1996), where gcd for the greatest

common divisor. This simple graph dynamics can be

used to construct the artiﬁcial CPGs by implementing

OBB modules as asymmetric Hopﬁeld-like networks,

where operating sinks can be regarded as ﬁring neu-

rons in purely inhibitory neuronal networks.

2.2 Dynamics of an OBB Module

An OBB module is deﬁned to have a pair of r

-sink

and r

-sink nodes, n

and n

, sharing the number of

resources. The postsynaptic membrane potential

of neuron i at t instant, M

(t), depends on three fac-

tors, i.e., the potential at the last instant M

(t − 1), the

impact of its coupled neuron output v

(t − 1), and the

negative feedback of neuron i itself v

(t − 1), with-

out considering the external impulse. The selection

of system parameters, such as the neuron thresholds

and synapse weight, are crucial for modelling. In

our model, let r = max(r

) and r

′

= h(r), where

h is a function of highest integer level and multi-

plying it by 10, e.g., if r

= 81 and r

= 341 then

′

= h(r) = h(max(81,341)) = h(341) = 10

. We can

further design neuron i and j’s thresholds θ

, θ

and

their synapse weights w

, w

as follows,











= max(r

)/(r

+ r

− gcd(r

))

= max(r

)/r

′

= (min(r

) − 1)/(r

+ r

− gcd(r

))

= min(r

)/r

′

(1)

The difference equation in the discrete time domain

of this system can be formulated as follows: each

neuron’s self-feedback strength is w

= −w

, w

j j

−w

. The activation function is a sigmoidal Heavi-

side type. It is worth noticing that k is a local clock

pulse of each neuron, a global clock is not required.

Thus we have,



(t + 1) = M

(t) + w

(t)

(t + 1) = M

(t) + w

j j

(t)

(2)

where,



(t) = max(0,sgn(M

(t) − θ

))

(t) = max(0,sgn(M

(t) − θ

))

(3)

We consider the designed circuit as a conservative dy-

namical system in an ideal case. The total energy is

constant, no energy loss or complement is allowed.

The sum of two neurons’ postsynaptic potential at any

given time instant is normalised to one. It is clear that

this system has the capability of self-organised oscil-

lation with the ﬁring rate of each neuron arbitrarily

adjustable.

If a neuron has more than one connections, then

its ﬁring state depends on the interactions of all the

connections,

(t) =

∏

j=1

(t) (4)

For instance, neuron i in Fig. 1 has connections with

both neuron j and k, the output of i is expressed as

(t) = v

(t) × v

(t), here v

(t) and v

(t) are obtained

from the above dynamical equations.

3 QUADRUPEDAL GAIT MODEL

Generally seven types of primary gait patterns are

identiﬁed for a quadruped in literature (Alexander,

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

1984). These can be summarised in Table 1.

Table 1: Quadrupedal primary gaits and description.

Pattern description

Gaits Ipsilateral legs Contralateral legs

walk quarter cycle out half cycle out

trot half cycle out half cycle out

pace in phase half cycle out

gallop half cycle out quarter cycle out

bound half cycle out in phase

pronk in phase in phase

jump quarter cycle out in phase

The proposed CPG model, with adaptable, different

model parameters, is able to generate all the gait pat-

terns shown in Table 1. The signals selecting gaits

and controlling transitions in the CPG, usually in the

spinal cord, come from the higher neural level in the

prefrontal, premotor and motor cortices following the

dog’s interaction with its environment.

Figure 2: Trot gait of a dog.

We choose a dog’s risk-avoiding behaviour to build a

case study of an CPG model which is made of the

OBB modules. Suppose a dog is initially wander-

ing around in a walk gait. Suddenly it is frightened

by something and makes an abrupt left turn and es-

capes with a faster trot gait (Fig 2). In this scene the

dog’s trajectory includes three different stages in se-

quence: walk, left turn (a special gait) and trot. These

locomotion behaviours are controlled by the different

motor driving outputs from its CPG. The activity of a

dog’s leg is simpliﬁed and generated by the activity of

a ﬂexor and an extensor motor neuron, respectively.

The ﬁring of a neuron in the OBB drives the ﬂexor

which lifts the leg from the ground in a swing stage.

The idleness of a neuron activates the extensor which

lands the leg on the ground in a stance stage.

The OBB network topologies for the rhythmic

pattern generation, and the phase relationship for

aforementioned three gait patterns are shown in Fig 3,

where the ﬁring cell (gray colour) denotes its corre-

sponding leg is lifting from the ground. In the right,

black-white bar, black bars specify the ﬁring of ﬂex-

ors while white ones for the ﬁring of extensors. It is

clear that the special, left turn gait has a gait pattern

circulation as shown in Fig. 1.

Head

LF RF

LH RH

(a)

(b)

(c)

Figure 3: The schematic diagram of three gaits and their

phase relations. The little black circles denote the shared

resources, gray cells are ﬁring and white ones are idle. The

left side topology is only one conﬁguration of a circulation

period of a pattern. RF - right front, RH - right hind, LF -

left front, LH - left hind. (a) walk, (b) left turn, (c) trot. .

From the biological knowledge we know that locomo-

tion speed is decided by both the coordinated phase

relation among legs and the duty factor, which is the

proportion of an extensor’s ﬁring duration in one pe-

riod. When an animal’s locomotion speed increases,

the extensor ﬁring time (corresponding to stance) will

decrease drastically while the ﬂexor ﬁring time (to

swing) keeps basically constant (Pearson, 1976). This

results in a lower duty factor, a relatively longer swing

stage and a faster locomotion speed. As the same with

adjusting coordinated phase relationship, the duty fac-

tor can also be modiﬁed by changing the reversabili-

ties of two coupled cells.

4 SIMULATION RESULTS

A schematic circuit diagram of OBB-based asymmet-

ric Hopﬁeld-like neural network is shown in Fig. 4.

A computer simulated example of quadruped risk-

avoiding behaviour is conducted using this network

and the pre-deﬁned cell reversabilities. There are to-

tally six possible connections between any two cells

in this CPG architecture (as shown in Fig. 3), among

which four connections are selected for a given gait

pattern. The selecting signals, labelled from a

, control the selection of an individual connection,

respectively, and come from the higher cortex. The

change of these signals denotes a change of connec-

tion topology. This change, together with the change

of reversabilities of the cells, decides the transition of

gait patterns.

SELF-ORGANISATION OF GAIT PATTERN TRANSITION - An Efficient Approach to Implementing Animal Gaits and

Gait Transitions

Figure 4: Quadruped CPG architecture. The cell output V

, V

correspond to LF, LH, RH, RF respectively. The pre-

deﬁned cell reversabilities are r

= r

= 1 for the walk and trot gaits, r

= r

= 2 and r

= r

= 1 for the left turn

gait. The initial membrane potentials are M

(0) = M

(0) = 0.45, M

(0) = M

(0) =

(0) = M

(0) = 1.05, M

(0) = 0.55, M

(0) = 0.95. The gait select signals are [a1,a2,a3,a4,a5,a6] = [111001] for walk

and trot, [001111] for left turn. The cell thresholds and weights follow equation 1.

An array of twelve comparators, three for a cell, is

used to compare the sub-cells’ membrane potentials

with thresholds. If a connection is absent then the

relative comparator is disabled. The enabled connec-

tions of a cell converge to an AND gate, to implement

equation 4 for the cell output. If a cell has an output,

this output will make three OR gates, corresponding

to its connections with all rest cells, have an output.

These OR gate outputs are selected by the control sig-

nals from CNS at an array of AND gates, whose val-

ues are fed to an array of swithes, and form a loop to

the input weight matrix for the comparator array.

According to equation 4, The output of a cell is

the multiplication of two terminal outputs connecting

with the cell’s two neighbours. A cell will ﬁre if and

only if its sub-cells are ﬁring simultaneously. An ad-

ditional control (not shown) is needed to ensure that

all shared resources on an edge will not reverse un-

less the output of a cell is ﬁring. The system param-

eters are given in the legend of Fig. 4. The choice

of initial membrane potential for every sub-cells is to

make all cells work, i.e., being ﬁring or idle, in an

appropriate conﬁguration of a starting gait’s circula-

tion period. After the choice of the membrane poten-

tials the system will run adaptively in its gait transi-

tion which is controlled by the CNS signals. There

is a self-organisation period observable in Fig. 5 from

walk to left turn gait. Another self-organisation be-

tween left turn to trot should exist whose effect may

be minimised if the system parameters are occasion-

ally appropriate for the next locomotion pattern at the

transition time instant.

5 CONCLUSIONS

We have presented a novel central pattern generator

model capable of generating a whole range of legged

locomotion gait patterns. This CPG architecture is

generalisable to mimic any gait patterns of any legged

animals from biped to centipede. Self-oganisation in

gait transition is observed in control of a limited num-

ber of signal ﬂow bits from the high level cortex. This

modular system is simple and highly compatible to

circuit implementation.

ACKNOWLEDGEMENTS

This work is supported by a British EPSRC grant

EP/E063322/1, a Chinese NSF grant 60673102 and

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

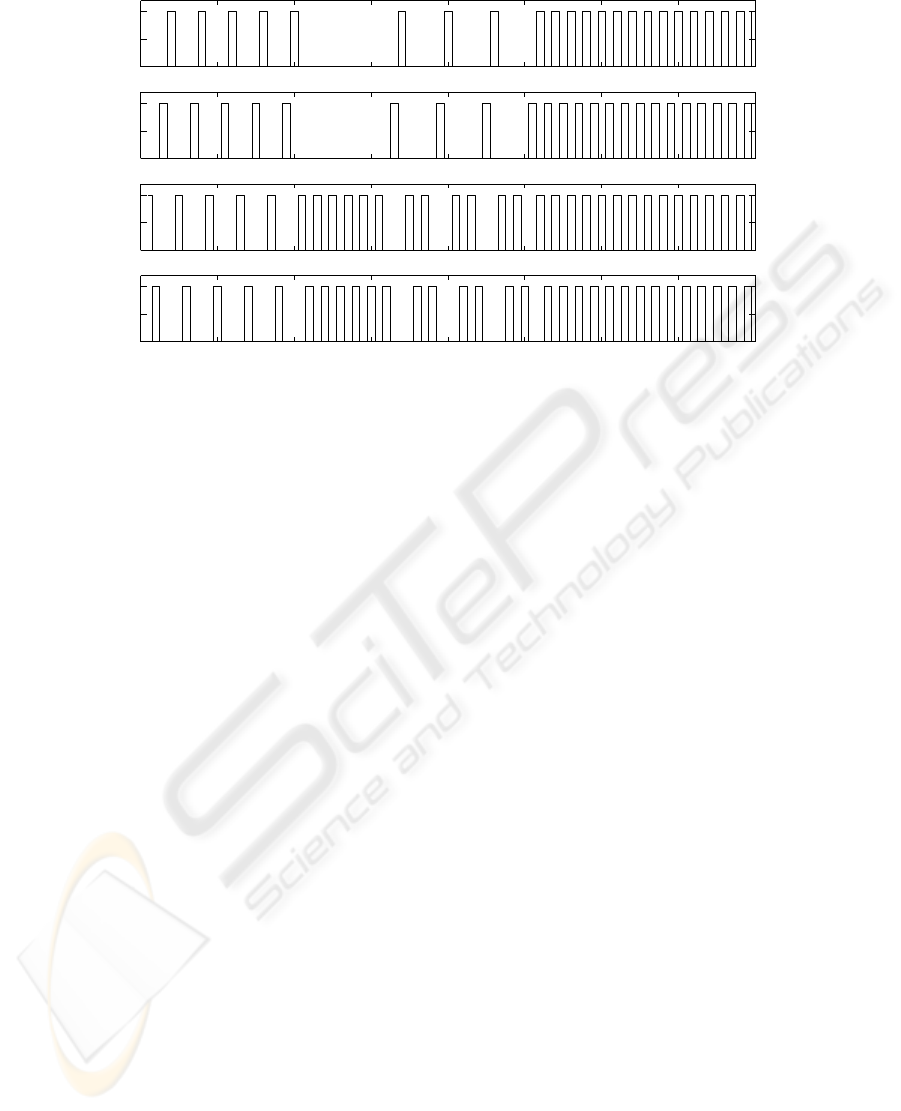
0 1 2 3 4 5 6 7 8

0.5

LF cell

0 1 2 3 4 5 6 7 8

0.5

LH cell

0 1 2 3 4 5 6 7 8

0.5

RH cell

0 1 2 3 4 5 6 7 8

0.5

RF cell

Time (second)

Figure 5: Cell output. Cell activity is equivalent to ﬂexor activity and contrary to extensor activity in phase. The virtual dog

starts with walk for 2 seconds. After that the left turn gait lasts for 3 seconds, which include a one-second self-organisation

period. From the ﬁfth second on it uses the faster trot gait to avoid the risk.

a Jiangsu Province grant BK2006218. We thank the

useful discussions with Dr. Felipe M.G. Franca and

Mr. Rodrigo Rodovalho.

REFERENCES

Alexander, R. (1984). The gait of bipedal and quadrupedal

animals. Intl J. Robotics Research, 3:49–59.

Aristotle (Translated version of 1936). On Parts of Ani-

mals, Movement of Animals, Progression of Animals.

By A.S. Peek and E.S. Forster (translators). Cam-

bridge, MA: Harvard University Press.

Barbosa, V. (1996). An introduction to distributed algo-

rithms. Cambridge, MA: The MIT Press.

Bay, J. and Hemami, H. (1987). Modeling of a neural

pattern generator with coupled nonlinear oscillators.

IEEE Trans. Biomedical Engr., 34:297–306.

Collins, J. and Stewart, I. (1993). Coupled nonlinear oscil-

lators and the symmetries of animal gaits. Journal of

Nonlinear Science, 3:349–392.

Golubitsky, M., Stewart, I., Buono, P., and Collins, J.

(1998). A modular network for legged locomotion.

Physica D, 115:56–72.

Grillner, S. (1985). Neurobiological bases of rhythmic mo-

tor acts in vertebrates. Science, 228:143–149.

Linkens, D., Taylor, Y., and Duthie, H. (1976). Mathemat-

ical modeling of the colorectal myoelectrical activity

in humans. IEEE Transactions on Biomedical Engi-

neering, 23:101–110.

Pearson, K. (1976). The control of walking. Scientiﬁc

American, 235:72–86.

Pearson, K. (1993). Common principles of motor control in

vertebrates and invertebrates. Annual Review of Neu-

roscience, 16:265–297.

Stein, P. (1978). Motor systems with speciﬁc reference to

the control of locomotion. Annual Review of Neuro-

science, 1:61–81.

Tsutsumi, K. and Matsumoto, H. (1984). A synaptic mod-

iﬁcation algorithm in consideration of the generation

of rhythmic oscillation in a ring neural network. Bio-

logical Cybernetics, 50:419–430.

Yang, Z. and Franca, F. (2003). A generalized locomotion

cpg architecture based on oscillatory building blocks.

Biological Cybernetics, 89:34–42.

Yang, Z. and Franca, F. (2008). A general rhythmic pattern

generation architecture for legged locomotion, In Ad-

vancing artiﬁcial intelligence through biological pro-

cess applications (A. Porto, A. Pazos, W. Buno, edi-

tors). Hershey, PA: Idea Group Inc.

SELF-ORGANISATION OF GAIT PATTERN TRANSITION - An Efficient Approach to Implementing Animal Gaits and

Gait Transitions