PARALLEL MACHINE EARLINESS-TARDINESS SCHEDULING

Comparison of Two Metaheuristic Approaches

Marcin Bazyluk, Leszek Koszalka

Chair of Computer Systems and Networks, Wroclaw University of Technology, Wyb. Wyspianskiego 27, 50-370 Wroclaw, Poland

Keith J. Burnham

Control Theory and Applications Centre, Coventry University, Coventry, U.K.

Keywords:

Task scheduling, parallel machines, heuristics, genetic algorithms, tabu search.

Abstract:

This paper considers the problem of parallel machine scheduling with the earliness and tardiness penalties

(PMSP

E/T) in which a set of sequence-independent jobs is to be scheduled on a set of given machines to

minimize a sum of the weighted earliness and tardiness values. The weights and due dates of the jobs are

distinct positive numbers. The machines are diverse - each has a different execution speed of the respective

jobs, thus the problem becomes more complex. To handle this, it two heuristics are employed, namely: the

genetic algorithm with the MCUOX crossover operator and the tabu search. The performances of the both

approaches are evaluated and their dependency on the shape of the investigated instances examined. The

results indicate the signiﬁcant predominance of the genetic approach for the larger-sized instances.

1 INTRODUCTION

The problem of job scheduling on parallel machines

(PMJS) has been considered recently in many scien-

tiﬁc and industrial communities. In the classical ex-

ample of this type of problem the collection of inde-

pendent jobs is investigated. Each of the tasks is to

be assigned to the single set of the available machines

which may beidentical or different. The problem con-

sidered here extends the PMJS with the weighted ear-

liness and tardiness penalties calculated for the exe-

cution of a job before or after its due date. A single

job consists of the following parameters, namely its

weight, also deﬁned as the importance, and its due

date. Baker and Scudder (Baker and Scudder, 1990)

provide a survey on the job scheduling problem in-

volving a due date determination. In this paper, the

due date for the each job is considered as a speciﬁc

moment in the time. If a given job is accomplished

at its due date, the requirements are fulﬁlled and the

penalty is not subjected. The speciﬁcation of a single

machine is implemented as a vector describingits pro-

cessing speed of the individual jobs. It is to be noted,

that the identical machines are characterized by the

identical vectors.

In the case, when the due dates of all of the jobs

are set to 0 (thus all the jobs require the fastest pos-

sible execution with no earliness penalty) and their

weights are equal, the problem considered is NP-hard

(Du and Leong, 1990). It is to be remarked, that when

the weights are arbitrary positive numbers, the task

becomes NP-hard in a strong sense. On the other

hand, the problem considered here may be thought of

as even more complex. Kanet examined the problem

of minimizing the total weighted earliness with the

tardiness on a single machine and common due dates

in (Kanet, 1981). He proposed the algorithm charac-

terized by a polynomial complexity. His work was

extended by Hall and Posner to the case of several

identical machines in (Hall and Posner, 1991). This

paper forms a further extension with the due dates al-

lowed to be different.

The example solution to the problem considered,

is a schedule of all jobs that are assigned to the sepa-

rate machines in a set of queues - one for each ma-

chine. The premise is to minimize the sum of the

penalties for all the jobs. The penalty for a single job

is calculated according to the Equation (1) where p

and w

are the penalty and the weight of the job i, re-

spectively. e

= max{0, d

− c

} denoted the earliness

of the job i and t

= max{0, c

− d

} is the tardiness

of the job i with d

being its corresponding due date

Bazyluk M., Koszalka L. and J. Burnham K. (2008).

PARALLEL MACHINE EARLINESS-TARDINESS SCHEDULING - Comparison of Two Metaheuristic Approaches.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 80-85

DOI: 10.5220/0001476500800085

 SciTePress

and c

its completion time (the time instant when the

processing of a job has been ﬁnished). The follow-

ing formula is introduced, see (2), accounting for the

total earliness and tardiness penalty (p), where I de-

notes the set of jobs.

= w

+ w

(1)

p =

∑

i∈I

∑

i∈I

(2)

2 PROBLEM FORMULATION

Let the problem of the scheduling of the N indepen-

dent lobs on a set of M available parallel machines

be considered. Each job may be completed by any

of the available machines, however the time required

differs, in general, depending on the machine chosen.

If the job has been accomplished too early or too late,

the penalty is calculated for the earliness or tardiness,

respectively, according to the difference between the

due date of the job and the real execution time. It

is noted, that the penalty is also proportional to the

weight of the particular job. By considering the pos-

sible decisions during the job scheduling procedure,

two optimization techniques have been developed to

minimize the total penalty for all the jobs. The mathe-

matical model presented here is a modiﬁcation of that

proposed by Cao, Chen and Wan in (Cao et al., 2005).

The next two subsections introduce the nomenclature

and the deﬁnitions required, to formulate the problem.

2.1 Known Parameters

i, j = 1, 2, . . . , N, job indeces

m = 1, 2, . . . , M, machine index

processing time of the i-th job on the m-th

machine, z

= {1, 2, . . ., 10}

weight of the i-th job ,

= {1, 2, . . ., 10}

due date of the i-th job ,

= {1, 2. . ., 5}

execution time of the i-th job

earliness of jo i, e

= max{0, d

− c

}

tardiness of jo i, t

= max{0, c

− d

}

2.2 Decision Variables

ijm



1 if job j follows job i on machine m,

0 otherwise,



1 if job i is executed by machine m,

0 otherwise,

i = 0, 1, . .. , N, j = 1, . . . ,N,

j 6= i, m = 1, . . . , M

With the decision variables deﬁned, the following

recursive formula (Equation (3)) is proposed for the

calculation of the moment of the job completion. The

job completion is deﬁned as the sum of its process-

ing time together with the moment when the job that

is executed directly before the one being considered

here, is completed.

∑

i=0

∑

m=0

ijm

+ z

(3)

2.3 Assumptions

Min T

∑

i=1

+ t

) (4)

∑

i=1,i6= j

∑

m=1

ijm

= 1 (5)

∑

i=1,i6= j

ijm

= y

, (6)

∑

j=1, j6=i

ijm

≤ y

(7)

+ A(1− x

ijm

) ≥ c

+ z

(8)

In all the assumptions introduced, the parameters are

deﬁned as follows:

i = 1, 2, . .. ,N, j = 1, 2, . .. , N, i 6= j,

m = 1, 2, . . . ,M, c

> 0, c

> 0

In the model presented, Equation (4) describes the ob-

jective function as the sum of the penalties for all the

jobs which are to be minimized. The following equa-

tions deﬁnes the restrictions to which the decision

variables and the parameters are subjected. Equation

(5) ensures that, ﬁrst, every job is processed on a sin-

gle machine and, second, that its execution is not di-

vided into separate parts. Equation (6) imposes a re-

striction that the j-th job must immediately followany

other job on the m-th machine (or be left in the ﬁrst

position in the case when i = 0). Thereby, the inter-

vals in the machine usage are not allowed. Equation

(7) states that, if the i-th job is processed on the m-th

machine, it will be immediately followed by at most

one other job on this machine. Therefore, the jobs

can be executed one at the each time instant. Equa-

tion (8) expresses the ﬁnite completion time of each

job, where the scalar A is a large positive number.

Due to the evident complexity of the problem con-

sidered, the investigations are restricted to the class of

heuristic algorithms. In Sections 3–4 two heuristic

based approaches are presented.

PARALLEL MACHINE EARLINESS-TARDINESS SCHEDULING - Comparison of Two Metaheuristic Approaches

START

• Find the ﬁrst solution.

LOOP

• Find the best solution which is not tabu.

• Update the global best solution.

• Add a rule to the tabu list.

• If the ﬁxed number of the iterations are completed,

STOP;

else if the ﬁxed number of the iterations without the

improvement regarding the the best global solution is

completed, STOP;

else repeat LOOP.

Figure 1: Tabu search algorithm.

3 TABU SEARCH ALGORITHM

APPROACH

The tabu search algorithm (TSA) was developed

mainly due to the work of the Polish mathematicians,

namely E. Nowicki and C. Smutnicki (Nowicki and

Smutnicki, 2005). It belongs to the class of local

search algorithms, where a concept of the local neigh-

bourhood of a given solution is considered. The local

neighbourhood is deﬁned as a set of solutions that are

different from the basic solution with respect to a sin-

gle attribute. Many different types of neighbourhood

can be found in the literature, however the swap and

insert types, are considered in this paper.

TSA consists of the subsequent steps to determine

the best representative of the neighbour solutions set,

where a single step is conducted in each iteration. It

may occur that one of the neighbour solutions is su-

perior in respect to the basic solution (i.e. the solution

which the neighbourhood is considered at the given

iteration). In this case, the step is made towards the

direction of the newly found neighbourhood solution.

This, therefore, allows the algorithm to alleviate the

possibility to be trapped in local extremes of the ob-

jective function considered. To avoid repetitive steps

between the same solutions in the adjacent extremes,

the tabulist consisting of the assumed a priori number

of the rules regarding the quality of the solutions vis-

ited recently, is proposed. Figure 1 provides a more

formal description of the proposed algorithm.

There exists, however, an exception when the so-

lution found is superior to the best one to date. In this

case the algorithm steps towards its direction uncon-

ditionally and the tabu list is erased. It is remarked,

that a considerable amount of time is required to esti-

mate even a single solution in each iteration of the al-

gorithm, for the instances relatively large. This leads

START

• Generate the ﬁrst population.

LOOP

• Find the best chromosome in the current population.

• Update the global best chromosome.

• Choose the representing chromosomes for the

crossover.

• Create a new population.

• Execute a swap mutation with the ﬁxed probability.

• Execute a bit mutation with the ﬁxed probability.

• If the ﬁxed number of the iterations are completed,

STOP;

else if the ﬁxed number of the iterations without the

improvement regarding the the best global solution is

completed, STOP;

else repeat LOOP.

Figure 2: Genetic algorithm.

to the conclusion that the quality of the ﬁrst generated

solution from which the algorithm starts is essential.

In this paper, a modiﬁed algorithm is suggested, to

handle this task.

The swap move is carried out via the exchange

of the positions between two randomly chosen jobs

taken from the list assigned to a single machine. In-

sert one removes a random job from a one machine

and allocates it on the second machine, directly be-

fore randomly chosen job from its list.

4 GENETIC ALGORITHM

APPROACH

For more details on the subject of the genetic algo-

rithms (GAs), see (Schmitt, 2000) and (Davis, 1991).

Due to the fact that many different approaches have

been described in the literature for solving the prob-

lem considered, this section presents the exact param-

eters of the algorithm implemented.

The more formal deﬁnition of the algorithm pro-

posed is presented in ﬁgure 2. The crossover operator

is the basis of the genetic algorithms, hence, it is es-

sential to focus on its proper implementation. The is-

sue that was shown experimentally in (Bazyluk et al.,

2006) for a simpler type of job scheduling problem

is that the utilization of a popular PMX leads to an

impossibility to obtain satisfying results. Therefore,

the multi-component uniform order-based (MCUOX)

crossover operator proposed by Sivrikaya and Ulusoy

in (Sivrikaya-Serifogluand Ulusoy, 1999) was chosen

for the purpose of this paper.

It is noted, that in the scheme chosen a single gene

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

accommodates both the object and the associated se-

lection associated with this object. In the case of the

problem considered, this refers to the situation where

each gene corresponds to the job-machine pair. The

construction of a descendant from two parent chro-

mosomes is presented in Figure 3.

START

• With the ﬁrst position on the parents and the descen-

dant.

LOOP

• Choose one parent randomly.

• Find the ﬁrst job corresponding to the chosen parent

which has not been assigned to the descendant.

• If the machine assigned to the job is the same for both

parents, make the same selection for the job;

else choose one of the machines from the parents ran-

domly and assign the job to it.

• Assign the job-machine pair to the ﬁrst empty position

of the descendant.

• If all genes of the descendant chromosomes are set,

STOP;

else proceed to the next gene on the descendant and re-

peat LOOP.

Figure 3: MCUOX crossover algorithm.

The mutation implemented comprises two mecha-

nisms. The ﬁrst, randomly selects two positions on a

chromosome and exchanges their contents. The sec-

ond, incorporates the reassignment of the machine to

a randomly chosen job in a chromosome. It is to be

noted, that this operation may lead to the same ma-

chine selection as before.

The selection of the chromosomes for the

crossover from a population builds on a rule that the

probability of choosing a chromosome to be a par-

ent in the next generation is proportional to its ﬁtness.

The value of the ﬁtness function is for a given chro-

mosome is deﬁned by Equation (9) where K is the

size of the population and F

= CT

(k)

−1

the ﬁtness

function of the chromosome k that is inversely propor-

tional to the objective function with C being a ﬁxed

constant.

Table 1: Experiment parameters.

tabu list size (TSA) 10

population size (GA) 25

swap mutation probability (GA) 0,1

bit mutation probability (GA) 0,05

crossover probability (GA) 0,9

∑

k=1

(9)

The appropriate tuning of the parameters of the GA

is one of the crucial issues that inﬂuences signiﬁ-

cantly its efﬁciency and effectiveness, see (Grefen-

stette, 1986) for more detailed discussion. For this

purpose, in the problem considered, a meta-genetic

algorithm with a regular PMX operator was addition-

ally implemented.

5 NUMERICAL ANALYSIS

5.1 Generation of Test Instances

Both implemented algorithms were validated for the

same instances of the various sizes considered. Due

to the fact that no benchmark problems were found

in the literature, such as in particular the presented

shape, the test benchmarks were generated randomly.

After the tuning of the parameters the following val-

ues, presented in Table 1, were set.

5.2 Research Results

The implemented algorithms were evaluated on a

IBM-compatible machine, equipped with the Intel

Pentium M 740 1, 73GHz processor and 512 Mbytes

of RAM. The ﬁrst experiment was conducted for a

set of 100 small instances comprising of 10 jobs and

3 machines. The evolution of the average objective

function, denoted (T

), for the both algorithms is de-

picted in Figure 4. It is observed, that TSA begins

with the solution that is nearly twice as large as T

however it relatively quickly overtakes GA (ﬁrst in-

tersection of the graphs in Figure 4). This property

can be noted for all the instances consisting of the job

sizes 100 or less, in general. In the case of TSA, as

opposed to GA, it seems less difﬁcult to determine

the optimal solution, but, on the other hand, signiﬁ-

cantly more computation time is required. This is due

to the property of the slow movement across the ar-

guments area of the TSA based algorithm. It is to be

remarked, that the aforemention drawback of TSA is

not signiﬁcant for the relatively small instances. It can

be expected that the GA would obtain the solution of

a similar quality as the TSA after a certain number

of iterations, which can be observed in Figure 5 (the

second intersection).

In the following investigation the impact is placed

to examine the two aforementioned intersection

PARALLEL MACHINE EARLINESS-TARDINESS SCHEDULING - Comparison of Two Metaheuristic Approaches

0 20 40 60 80 100

150

200

250

300

350

400

450

500

iteration

average Tc

tabu search

genetic algorithm

Figure 4: Objective function evolution.

points. In all the experiments conducted the three ar-

eas of the objective function evolution were observed:

1. predominance of GA in the ﬁrst iterations (up to

the 1st intersection)

2. predominance of TSA for a given set of iterations

(up to the 2nd intersection)

3. predominance of GA again (after the 2nd intersec-

tion)

The purpose of the following investigation is to ana-

lyze the location of the both intersection points with

the accordance to the size of the particular instance.

Analogously to the results presented previously,

see Figures 4-5, the ﬁrst intersection is observed rela-

tively quickly (it is a one of the ﬁrst iterations) when

the instances smaller than 100 jobs and 10 machines

are considered. Therefore, the usage of the TSA has

proven to be a considerably better choice, when the

relatively short calculation time is to be expected. On

the other hand, in the cases when the location of the

optimum solution is of the prime interest, the GA al-

gorithm is the more appropriate choice. The radi-

cal changes are observed for the relatively large in-

stances of 100 jobs or more. In these cases, the TSA

is not able to move sufﬁciently fast across the argu-

ments area and, thus, the ﬁrst intersection point, after

a larger number of iterations, is reached. The example

average objectivefunction evolution for 100 instances

of 200 jobs and 10 machines is presented in Table

2. It is noted, that with the growth of the instance

size, the corresponding time required for a comple-

tion of a single iteration increases, accordingly. Af-

ter 10 iterations it may be readily observed that the

TSA evolved from 59509 to 59137 with the decrease

of 0, 63%. On the other hand, the utilization of the GA

leads to the decrease from 55828 to 54381 at the ratio

of 2, 59%. The time required for carrying out the ex-

periment in the same conﬁguration setup, for the time

0 50 100 150 200 250 300 350 400

150

200

250

300

350

400

450

500

iteration

average Tc

tabu search

genetic algorithm

Figure 5: Objective function evolution.

0.5

1.5

machines no.

jobs no.

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

1.2

Figure 6: Effectiveness proportion of GA to TSA for differ-

ent instance sizes.

long enough to reach the ﬁrst intersection point, was

approximately calculated to be few hours.

Table 2: Objective function evolution.

Iteration T

(TSA) T

(GA)

1 59509 55828

2 59470 55016

3 59396 54859

4 59346 54758

5 59315 54670

6 59271 54539

7 59243 54529

8 59210 54455

9 59174 54410

10 59137 54381

The further work will comprise the investigation of

the three-dimensional graphs to illustrate the compar-

ison results as a function of the both attributes of the

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

machines no.

jobs no.

iteration

Figure 7: Location of ﬁrst intersection point for different

instance sizes.

instance size i.e. the number of the jobs and the num-

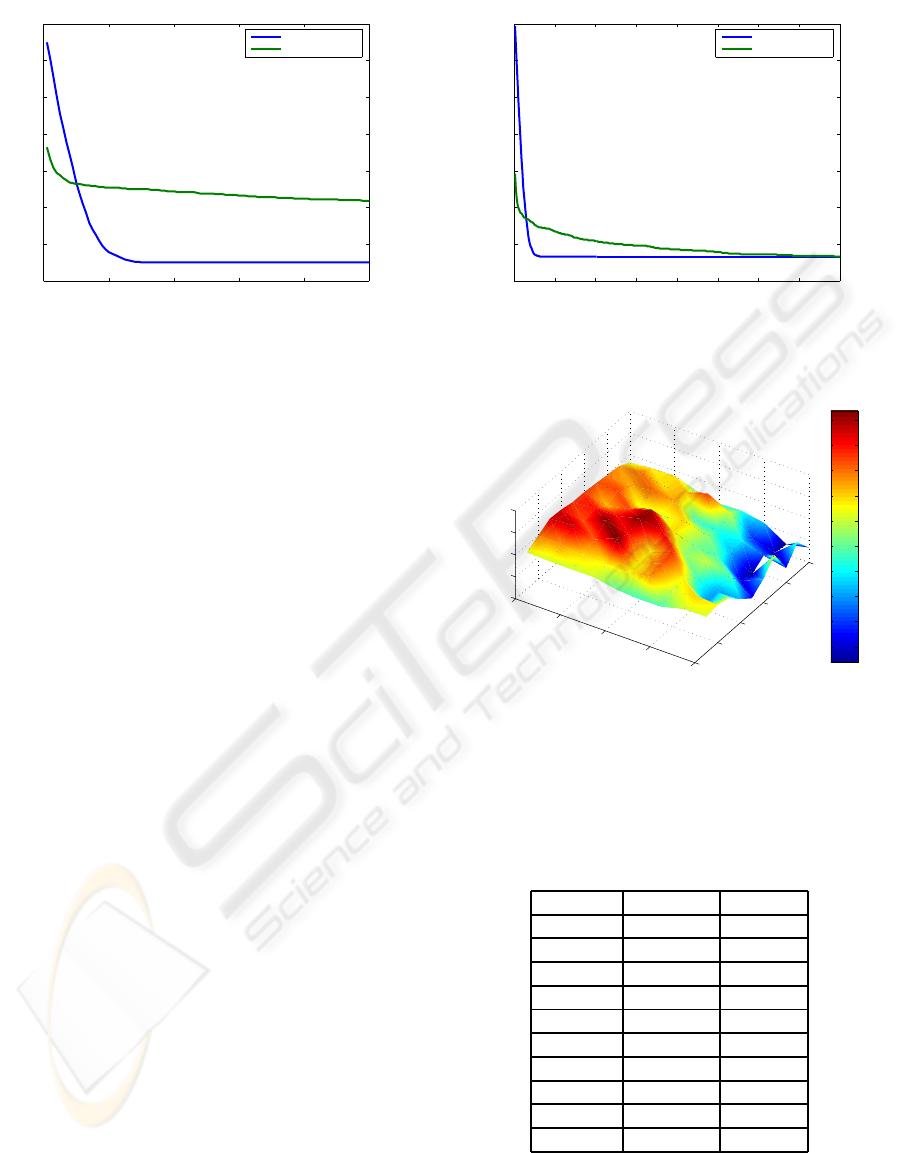
ber of the machines. Figure 6 illustrates the propor-

tion, denoted (F), of the objective function value ob-

tained via the GA and the TSA. The experiment was

carried out for 100 instances of the each size taken

from the set of 1 to 10 machines and 10 to 50 jobs.

Both algorithms were investigated for 25 iterations.

The value of F > 1 on the graph corresponds to the

situations where the efﬁciency of GA was superior to

TSA, F < 1 otherwise.

Figure 7 presents the average number of iterations,

when the ﬁrst intersection was observed. The ﬁrst in-

tersection point can be interpreted as a point starting

from which the GA is superior over the TSA.

6 CONCLUSIONS

In the paper the problem of the parallel machine job

scheduling with the weighted earliness and tardiness

has been addressed. Two heuristic algorithms, that

proven to be efﬁcient, have been proposed and nu-

merically validated. The investigation of the sensitiv-

ity of both approaches as a function of the size of the

problem instance, has been carried out. The results

obtained suggest that the TSA is appropriate to han-

dle the relatively small and medium instances. On

the other hand, utilization of the GA coupled with

MCUOX crossover operator, becomes more beneﬁ-

cial with the increase of the problem instances. An

important property was observed, namely a signiﬁ-

cant deterioration of the efﬁciency of the TSA for in-

stances containing 2−5 machines in comparison with

other values was noted, see Figures 6-7. Considering

these ﬁgures from the instance of (1 machine, 10 jobs)

to (10 machines, 50 jobs) a constant improvement of

the GA in comparison with the TSA up to the point of

its predominance, can be seen. It has been shown ex-

perimentally that the point is located in the vicinity of

the instance size of 100 and 200 jobs, see (Figure 5).

Furthermore, the execution time of GA with MCUOX

increases with a decreasing rate as a function of the

increasing problem size whilst the increasing rate is

observed for the TSA.

The problem extension could consist of the se-

quential dependency of jobs and the possibility of in-

troducing the idle time intervals between subsequent

execution of jobs. Further improvement of the pro-

posed heuristics can be achieved by considering a hy-

brid algorithm that inherits the advantages of both ap-

proaches i.e. the GA and the TSA.

REFERENCES

Baker, K. and Scudder, G. (1990). Sequencing with ear-

liness and tardiness penalties: a review. Operations

Research, 38:22–36.

Bazyluk, M., Koszalka, L., and Burnham, K. (2006). Using

heuristic algorithms for parallel machines job schedul-

ing problem. Computer Systems Engineering.

Cao, D., Chen, M., and Wan, G. (2005). Parallel ma-

chine selection and job scheduling to minimize ma-

chine cost and job tardiness. Computers and Opera-

tions Research, 32:1995–2012.

Davis, L. (1991). Handbook of Genetic Algorithms. Van

Nostrand Reinhold, New York.

Du, J. and Leong, J. (1990). Minimizing total tardiness on

one machine is np-hard. Mathematics of Operations

Research, 483–495:1990.

Grefenstette, J. (1986). Optimization of control parameters

for genetic algorithms. IEEE Transactions on Systems

Man and Cybernetics, SMC-16:122–128.

Hall, N. and Posner, M. (1991). Earliness-tardiness schedul-

ing problems, i: weighted deviation of completion

times about a common due date. Operations Research,

39:836–846.

Kanet, J. (1981). Minimizing the average deviation of job

completion times about a common due date. Naval

Research Logistics Quarterly, 28:643–651.

Nowicki, E. and Smutnicki, C. (2005). Metaheuristic op-

timization via memory and evolution. Kluwer Aca-

demic Publishers, pages 165–190.

Schmitt, L. (2000). Theory of genetic algorithms. Theoret-

ical Computer Science, 259:1–61.

Sivrikaya-Serifoglu, F. and Ulusoy, G. (1999). Parallel ma-

chine scheduling with earliness and tardiness penal-

ties. Computers & Operations Research, 26:773–787.

PARALLEL MACHINE EARLINESS-TARDINESS SCHEDULING - Comparison of Two Metaheuristic Approaches