
A NEW APPROACH OF GRAY IMAGES BINARIZATION FOR
ARTIFICIAL VISION SYSTEMS WITH THRESHOLD METHODS
Andrei Hossu and Daniela Hossu
University Politehnica of Bucharest, Faculty of Control and Computers
Dept. of Automatics and Industrial Informatics, 313 Spl. Independentei, sector 6, RO-77206, Bucharest, Romania
Keywords: Vision systems, Gray level image binarization, gray level histogram, global optimum thresholding, dynamic
optimum threshold, temporal histogram, temporal thresholding and moving scene in robotic automation.
Abstract: This paper presents some aspects of the (gray level) image binarization methods used in artificial vision
systems. It is introduced a new approach of gray level image binarization for artificial vision systems
dedicated to the specific class of applications for moving scene in industrial automation – temporal
thresholding. In the first part of the paper are remarked some limitations of using the global optimum
thresholding in gray level image binarization. In the second part of this paper are presented some aspects of
the dynamic optimum thresholding method for gray level image binarization. In the third section are
introduced the concepts of temporal histogram and temporal thresholding, starting from classic methods of
global and dynamic optimal thresholding of the gray level images. In the final part are presented some
practical aspects of the temporal thresholding method in artificial vision applications for the moving scene
in robotic automation class; highlighting the influence of the acquisition frequency on the methods results.
1 IMAGE BINARIZATION WITH
GLOBAL THRESHOLD
Threshold methods are defined as starting from the
analyse of the values of a function T of the type:
T = T [x, y, p(x, y), f(x, y)] (1)
Where:
f(x, y) – represents the intensity value of the
image element located on the co-ordinates (x, y);
p(x,y) – represents the local properties of the
specific point (like the average intensity of a region
centred in the co-ordinates (x, y)).
T – is the binarization threshold
The goal is to obtain from an original gray level
image, a binary image g(x, y) defined by:
⎩
⎨
⎧
≤
>
=
Tyxf
Tyxf
yxg
),(for 0
),(for 1
),(
(2)
For T a function only of f(x, y), the obtained
threshold is called global threshold.
In the case of T a function of both f(x, y) and p(x,
y), the obtained threshold is named local threshold.
In the case of T a function of all f(x, y), p(x, y), x
and y, the threshold is a dynamic threshold.
1.1 Intensity Level on Normal
Distribution Assumption
Gray level histogram represents the probability
density function of the intensity values of the image.
In order to simplify the explanations, we suppose
the image histogram of the gray levels is composed
from two values combined with additive Gaussian
noise:
- The first segment of the image histogram
corresponds to the background points – the intensity
levels are closer to the lower limit of the range (the
background is dark)
- The second segment of the image histogram
corresponds to the object points – the intensity levels
are closer to the upper limit of the intensity range
(the objects are bright).
The problem is to estimate a value of the
threshold T for which the image elements with an
intensity value lower than T will contain background
points and the pixels with the intensity value greater
than T will contain object points, with a minimum
error. For a real image, the partitioning between the
11
Hossu A. and Hossu D. (2008).
A NEW APPROACH OF GRAY IMAGES BINARIZATION FOR ARTIFICIAL VISION SYSTEMS WITH THRESHOLD METHODS.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 11-16
DOI: 10.5220/0001477200110016
Copyright
c
SciTePress

two brightness levels is not so simple and also not so
accurate. The partitioning is fully accurate only if
the two modes of the bimodal histogram are not
overlapped. The classification is defined as the
process of the distribution of the pixels in classes.
The goal of the binarization process is the
minimisation of the error of classification. The
optimum binarization threshold is located in the
intersection position of the two normal distributions.
The estimation of the error of classification is
obtained from the area of the overlapped segments:
image size
BA
E
+
=
(3)
Suppose the image contains two intensity level
values affected with additive Gaussian noise. The
mixture probability density function is:
)()()(
2211
xpPxpPxp
+
=
(4)
Where:
x – the random value representing the intensity
level,
p
1
(x), p
2
(x) – are the probability density
functions,
P
1
, Pp
2
- are the a priori probabilities of the two
intensity levels (P
1
+P
2
= 1).
For the normal distribution case on the two
brightness levels:
2
2
2
2
2
2
2
1
2
1
1
1
2
)(
exp
2
2
)(
exp
2
)(
σ
μ−
πσ
+
σ
μ−
πσ
=
xPxP
xp
(5)
Where:
)()()(
2211
xpPxpPxp
+
=
(6)
21
, μμ - are the mean values of the two
brightness levels (the two modes),
21
, σσ - are the standard deviations of the two
statistical populations.
Suppose the background is darker than the
object. In this case
21
μ<μ and defining a threshold
T, so that all pixels with intensity level below T are
considered belonging to the background and all
pixels with level above T are considered object
points. The probability of misclassification an object
point (classifying an object point as a background
point) is:
Similarly, E
2
:
dxxpTE
dxxpTE
T
T
)()(
)()(
12
21
∫
∫
∞+
∞−
=
=
(7)
The probability of error is given by:
)()()(
1221
TEPTEPTE
+
=
(8)
To find the threshold value for which the error is
minimum, E(T) is differentiate with respect to T:
tpPtpP ()(
2211
=
)
(9)
Applying the result to the Gaussian density we
obtain:
AT
2
+ BT + C = 0 (10)
Where:
22
11
2
2
2
1
2
1
2
2
2
2
2
1
2
12
2
21
2
2
2
1
ln
)(2
P
P
C
B
A
σ
σ
σσ+μσ−μσ=
σμ−σμ=
σ−σ=
(11)
If the standard deviations are equal, a single
threshold is sufficient:
1
2
21
2
21
ln
2 p
p
T
μ−μ
σ
+
μ+μ
=
(12)
If the probabilities are equal p
1
= p
2
the threshold
value is equal with the average of the means.
A way of checking the validity of the assumption
of bimodal histogram is to estimate the mean-square
error between the mixture density, p(x) and the
experimental histogram h(x
i
).
2
1
)]()([
1
i
N
i
i
xhxp
N
M −=
∑
=
(13)
Where: N – number of possible levels of the
image (usually N = 256)
The image binarization is obtained changing the
colour attribute of each pixel according to its
intensity level relative to the binarization threshold.
Characteristics of the global thresholding methods
(Borangiu, et al., 1994)., (
Haralick and Shapiro, 1992):
- The assumption that both classes have the same
standard deviation is acceptable, but the assumption
the classes (two levels) have the same a priori
probabilities in many applications is not acceptable.
In the case of the artificial vision systems
dedicated to object recognition for industrial
applications there is a large amount of a priori
information about the image that has to be
processed. Better results of estimation of the
distribution of the image elements of the scene
(background image, without the objects) can be
obtained. Usually, in robotic applications, the
illumination environment is known and controlled
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
12

and also the object classes with a probability of
apparition in the image are not known. In many
robotic application an estimation of the ratio
between the area of the objects to be analysed and
the total area of the image scene, can be made with
good results (a batter estimation than the assumption
of P
1
= P
2
= 0.5).
2 IMAGE BINARIZATION WITH
DYNAMIC THRESHOLD
There are some classes of scenes of artificial vision
systems where using the global threshold methods is
not acceptable:
• The case of the applications where the lighting
system does not supply a uniform intensity all over
the analysed surface.
• Segments of the image (or some times, image
elements) do not have the same behaviour in the
same lighting conditions.
For these types of images, for binarization of the
image, the most often used are dynamic threshold
methods. The methods are based on the local analyse
of the image. The algorithm of the estimation of the
dynamic threshold consist of:
• The original image is divided in regions of a
prescribed size.
• For each region it is estimated the histogram
• For each histogram it is estimated the error
induced from the assumption of bimodal histogram
(a histogram built from two normal distributions)
• If the value of the error is less than an
acceptable value, the global threshold for the region
is estimated.
• If the value of the error is too big (the
histogram is too far from a bimodal histogram) the
threshold value for binarization is estimated from the
interpolation of the neighbours region threshold
values (for which the assumption of a bimodal
histogram is considered acceptable).
• In the final stage, a second interpolation process
is applied: for each image element is assigned a
threshold value T(x, y) from the interpolation of the
values of the neighbour image elements.
The method is called dynamic thresholding
because the value of the resulted threshold for each
image element is dependent of the position of the
element in the image - T(x, y).
Characteristics of the dynamic thresholding
methods:
- Lack of processing time consumption – each
element of the image is used at least two times (the
method requires multiple-pass of the image) in
different steps of the algorithm (and the number of
the elements is very large).
- Estimation of the acceptable error value (or the
validation of the bimodal histogram assumption) is a
complex process.
- To choose the size of the image regions we
have to take into account:
- Large size of the region makes the method to
loose the dynamic threshold characteristics and to
fail into a global threshold method
- Small size of the region makes to loose the
statistical characteristic of the population of the
image elements contained by the analysed region
(and the accuracy of the results is lost).
The last comment on the method is the fact that
this method does not solve the problem of the non-
uniformity of the illumination system or of the
acquisition sensor.
3 TEMPORAL HISTOGRAM
For the class of artificial vision systems dedicated
for moving scene (used very often in inspection and
robotic applications) three types of image intensity
level distortions can be identified (Croicu, et al.,
1998), (Hossu, et al., 1998):
• Illumination non-uniformity (obtaining a
uniform intensity of the light on the whole area of
the scene where the image is analysed – usually 2 m
– it is practical impossible).
• Sensor non-linearity – for linear cameras with a
large number of pixels per row (2048 and more) can
be identified areas of non-linear behaviour of the
sensor (there are segments of the linear sensor with a
different behaviour of the elements sensitivity at
light intensity).
• Sensor cells non-uniformity – in cameras with
CCD sensor, the cells presents a different response
on sensitivity at light intensity related to their
neighbours
In Figure 1 are presented the image intensity
level distortions.
The main problem of the methods presented before
represents the assumption that the image is a
statistical population obtained from the addition of
two ore more distributions (in the general accepted
case normal distribution).
A NEW APPROACH OF GRAY IMAGES BINARIZATION FOR ARTIFICIAL VISION SYSTEMS WITH
THRESHOLD METHODS
13

Pixel value
Pixel value
Sensor non-linearity
Illumination non-
uniformity
Cell non-uniformity
Pixels row
Pixels row
Figure 1: Image intensity level distortions for CCD linear
camera acquisition.
In the general case (an array image) an image
represents a data set of:
{f(x, y) | x ∈ [0,N], y ∈ [0,M]}
(14)
where:
N represents the number of image elements per
row (number of image columns),
M represents the number of image elements per
column (number of image rows),
In the linear image case, this data set become:
{f(x) | x ∈ [0,N]}
(15)
where:
N represents the number of image elements per
row (number of image columns).
This assumption on the distribution of the
intensity levels has the starting point the assumption
that the insertion point of the noise is located on the
transmission level of the information. In other
words, the assumptions is that:
- The acquired image is an ideal image (with
only two gray levels: the gray level of the scene
pixels and the gray level of the pixels corresponding
to the object)
- Then a global noise is applied, transforming the
two levels in two normal distributions.
The assumption is false and using it we are
analysing a histogram, which is far away of two
normal distributions, and from here the results are
distorted. In reality the noise on the intensity level
has its insertion point on the acquisition level and
not on image transmission level. Intensity source has
the meaning of intensity signal on the acquisition
element and not only the lighting system. This
implies the fact that the noise on the intensity source
represents the whole chain of: lighting source noise,
reflective characteristics of the object surface and
reflective characteristics of the scene surface and the
sensitivity characteristics of the sensor. Moving the
insertion point of the noise we obtain: In the general
case (an array image) an image represents a data set
of:
{f
i
(x, y) | i ∈ [0,L]}
(16)
where:
L represents the number of the image frames (the
size of the statistic population analysed),
x ∈ [0,N], N representing the number of image
elements per row (number of image columns),
y ∈ [0,M], M representing the number of image
elements per column (number of image rows).
In the linear image case, this data set become:
{f
i
(x) | i ∈ [0,L]}
(17)
where:
L represents the number of the image frames (the
size of the statistic population analysed),
x ∈ [0,N], N representing the number of image
elements per row (number of image columns).
In this way several temporal built statistical
populations (from intensity levels of the same image
element on a set of image frames acquired on
different moments) replace the spatial built
statistical population (made from image elements of
the same image). The method of temporal histogram
has the result the fact that each element of this set of
histograms represents a bimodal histogram with two
not overlapped modes (in case of a correct
acquisition environment). It can be also introduce an
estimation of the quality of the acquisition and
binarization process using the estimation of the
misclassification error analysing the parameters of
the two normal distributions. The method offers also
the capacity of identification of the areas where
some modifications should be done (on the lighting
system) in order to improve the quality of the
acquisition and binarization process. The lack of the
proposed method is the memory consumption (it has
to be built N x M different histograms in array
acquisition, or N – in linear acquisition case). This
problem is not so restrictive because at the end only
the threshold values have to be stored and not the
whole histograms. Another restriction is the fact that
the method requires a large number of image frames
acquired for construction of the statistical
populations (in application set-up time). In the case
of the systems dedicated to industrial applications
usually this does not represent a real problem. This
type of applications does not require a system
response in condition of a small number of image
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
14
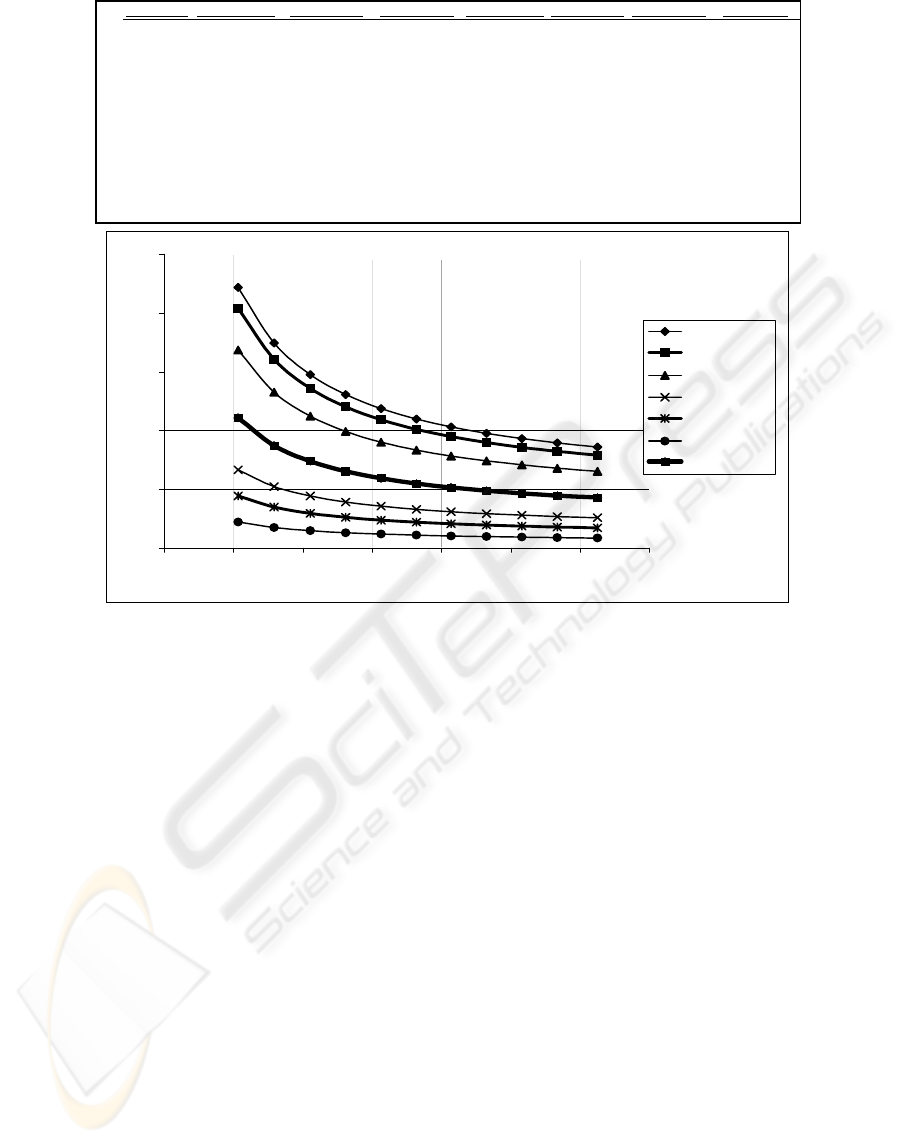
V [m/min] Object Min+ Object Max Object Min- Scene Min+ Scene Max Scene Min- Threshold
1 20,7 221,532847 203,810219 168,364964 66,459854 44,306569 22,153285 110,766423
2 25,9 174,338624 160,391534 132,497354 52,301587 34,867725 17,433862 87,169312
3 31,1 147,510373 135,709544 112,107884 44,253112 29,502075 14,751037 73,755187
4 36,2 130,479452 120,041096 99,164384 39,143836 26,095890 13,047945 65,239726
5 41,3 118,513120 109,032070 90,069971 35,553936 23,702624 11,851312 59,256560
6 46,4 109,644670 100,873096 83,329949 32,893401 21,928934 10,964467 54,822335
7 51,4 102,927928 94,693694 78,225225 30,878378 20,585586 10,292793 51,463964
8 56,5 97,474747 89,676768 74,080808 29,242424 19,494949 9,747475 48,737374
9 61,6 93,040293 85,597070 70,710623 27,912088 18,608059 9,304029 46,520147
10 66,7 89,363484 82,214405 67,916248 26,809045 17,872697 8,936348 44,681742
11 72,5 85,877863 79,007634 65,267176 25,763359 17,175573 8,587786 42,938931
Intensity levels relative to the scene speed
0
50
100
150
200
250
10 20 30 40 50 60 70 80
Speed V [m/min]
Intensity levels
Object Min+
Object Max
Object Min-
Scene Min+
Scene Max
Scene Min-
Threshold
Figure 2: The influence on the intensity levels of the speed of the scene (acquisition frequency).
frames a priori acquired. The vision systems
dedicated to industrial applications can take the
advantage on the fact that the image environment
does not change a lot in time. In this way it can be
initially reserved a certain time for acquiring a large
enough number of image frames in order to be able
to identify the permanent characteristics of the
environment. All the intensity level distortions
present permanent characteristics. Using this method
is a necessity for the artificial vision systems
dedicated to applications where the errors on
binarization are not acceptable. In the applications
dedicated exclusively to shape recognition the errors
are accepted in a predefined range.
4 BINARIZATION THRESHOLD
VALUE AFFECTED BY THE
ACQUISITION FREQUENCY
ON THE
In moving scene applications, in order to maintain a
constant resolution of the vision system along the
direction of the scene movement, it is necessary the
ratio between the acquisition frequency (the image
lines rate – in the case of a line scan camera) and the
scene speed to be constant. The acquisition
frequency determines the exposure time of the CCD
sensor cells. It can be notice an important influence
of the speed (of the conveyor) on the intensity level
of the same image element in the same lighting
environment. In Figure 2 are presented the
experimental results obtained analysing the
influence on the intensity levels (for both: bright
object and dark background) of the speed of the
conveyor (acquisition frequency). The results were
obtained on a statistical population from an image
element on each measured speed. The second
column represents the measured speed of the scene
(conveyor) – V [m/min]. The 3
rd
to 8
th
columns
represent image intensity levels estimated from the
analysed statistical population (temporal histogram).
The values from the Threshold column are the
binarization threshold values obtained from a global
optimum temporal thresholding method applied on
the histogram built for each analysed level of the
speed. In Figure 3 are presented graphical the
explanations on the meanings of the data involved in
the analysis of the influence of the speed
A NEW APPROACH OF GRAY IMAGES BINARIZATION FOR ARTIFICIAL VISION SYSTEMS WITH
THRESHOLD METHODS
15

(acquisition frequency) on the intensity levels. The
artificial vision system benefits from these results
using a relation between the value of the binarization
threshold and the speed V of the scene
T = T (x, V) (18)
Because of the response time restrictions
imposed to the artificial vision system, instead of
using an explicit expression of the estimated
function T(x, V), a search method in an a priori filled
table (at set-up time) is more appropriate. The size
of the table is 256 (the number of the possible values
of the binarization thresholds), containing floating-
point values of the speed of the conveyor
(acquisition frequency) for which the value of the
binarization threshold has to be changed.
Object Min-
Object Min+
Scene Min-
Scene Min+
Scene Max
Object Max
Threshold
Increased speed
influence on
intensity levels
Intensity level
Intensity level
N
umber of
pixels
N
umber of pixels
Figure 3: The influence of the speed on the intensity
levels.
5 CONCLUSIONS
For the class of artificial vision systems dedicated
for inspection and measurement industrial
applications the error on binarization process is not
acceptable. In this, case classic methods like global,
local and dynamic threshold are not applicable. The
paper introduces a new approach of gray level image
binarization – temporal thresholding. For the class of
artificial vision systems dedicated for moving scene
the acquisition frequency is dependent on the speed
of the transmission support (usually a conveyor). To
solve this problem, the artificial vision system has to
estimate the influence of the acquisition frequency
on the histogram and on the binarization threshold
values. The paper proposes a processing time
efficient method to estimate the binarization
threshold for the case of an error free vision system
in the case of variation of the acquisition frequency.
REFERENCES
Haralick, R., Shapiro, L. (1992) Computer and Robot
Vision, Addison-Wesley Publishing Company.
Borangiu, Th, Hossu A., Croicu, A. (1994) -
ROBOTVISIONPro, Users Manual, ESHED
ROBOTEC, Tel – Aviv.
Croicu, A., Hossu, A., Dothan, E., Ellenbogen, D., Livne,
Y. (1998)- ISCAN-Virtual Class based Architecture
for Float Glass Lines, IsoCE’98, Sinaia.
Hossu, A., Croicu, A., Dothan, E., Ellenbogen, D., Livne,
Y.(1998) - ISCAN Cold-Side Glass Inspection System
for Continuous Float Lines, User Manual, Rosh-
Haayn.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
16
