A NEW APPROACH FOR MODELING ENVIRONMENTAL

CONDITIONS USING SENSOR NETWORKS

Mehrdad Babazadeh and Walter Lang

Institute for Microsensors, -actuators and -systems (IMSAS), University of Bremen, Otto-Hahn-Allee, Bremen, Germany

Keywords: Temperature, relative humidity, air flow, estimation, grey-box, model.

Abstract: An approach to estimate environmental conditions (ECs), temperature, relative humidity and air flow in a

few desired sensor nodes in a wireless sensor network, slept for reducing battery-consumption or inactive

due to either empty batteries or out-of-range is presented. A nonlinear, multivariable model containing the

interconnections is extracted and using data of surrounding active sensor nodes is broken to the linear

models. Unknown parameters of the model are verified by a multivariable identification method. The

proposed approach is independent of the type of ventilation system. It can be used in different applications

such as designing model base ECs controllers as well as an estimator in fault diagnosis methods.

1 INTRODUCTION

Identification, modeling and control of Temperature

(T), relative Humidity (H) and air Flow (F) as the

environmental conditions (ECs) in the air

conditioned closed spaces have gained a lot of

attractions during the last few years. Therefore,

simple and precise mathematical models can play a

key role in these areas. Improving such linear

models or proposing new nonlinear models is very

vital on this issue. As the first step, we try to achieve

a simple mathematical model for the ECs using a

wireless sensor network established inside the

container loaded with freights. We utilize this model

to introduce a new technique to estimate the EC in

the place of some desired sensor nodes (DSNs).

They may be either in sleep mode or out of service.

As stated by the articles, there are three types of

models: based on (Sohlberg, 2003), White-box

models are made of theoretical considerations where

the grey-box models are extracted from the first

principles and parameters of the models are obtained

by measurement and black-box models are identified

only using measurement of the system input and

output. The methods achieved to the white, grey and

black-box models of T for air-handling units have

been addressed in

(Ghiaus, 2007) , (Shaikh, 2007),

(Brecht, 2005), (Desta, 2004), (Frausto 2004)

. Some

other works consider the effects of air flow pattern

on the T in special cases

(Moureh, 2004), (Rouaud,

2002)

and (Smale, 2006) is a brief review of numerical

models of airflow in refrigerated food applications.

(Desta, 2004) outlines a method to achieve an

accurate model of T in a closed space using both k-ε

model and a data-base mechanistic (DBM) modeling

technique. It doesn’t consider the effect of the heat

transfer from the neighboring zones.

All previous models are obtained between input

(inlet) and a point of corresponding space. As

attested by these methods, the ECs inside the

container will change only due to variation in inlet.

Some of the models obtained in the existing papers

either linear or nonlinear don’t consider all of

important parameters of the ECs. Furthermore,

particular conditions and the limit range of the

parameter variations are necessary and despite the

high precision, complexity makes them impractical

in some applications.

If return to model making in the mentioned

space, nonlinear multivariable nature and

interconnections between the variables of the ECs in

addition to the presence of the freight as an

unpredictable, immeasurable disturbance, effects of

dynamic of flow, surfaces and walls inside the

container increase complexity of the model which

we are looking for. Another important factor is

disturbance which can be appeared in the different

ways and may be cause a big estimation error: (i)

Opening the door of the container; (ii) changing

either direction or rate of the air flow by some

obstacles; (iii) thermal or moisturize influences of

Babazadeh M. and Lang W. (2008).

A NEW APPROACH FOR MODELING ENVIRONMENTAL CONDITIONS USING SENSOR NETWORKS.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 78-83

DOI: 10.5220/0001477800780083

 SciTePress

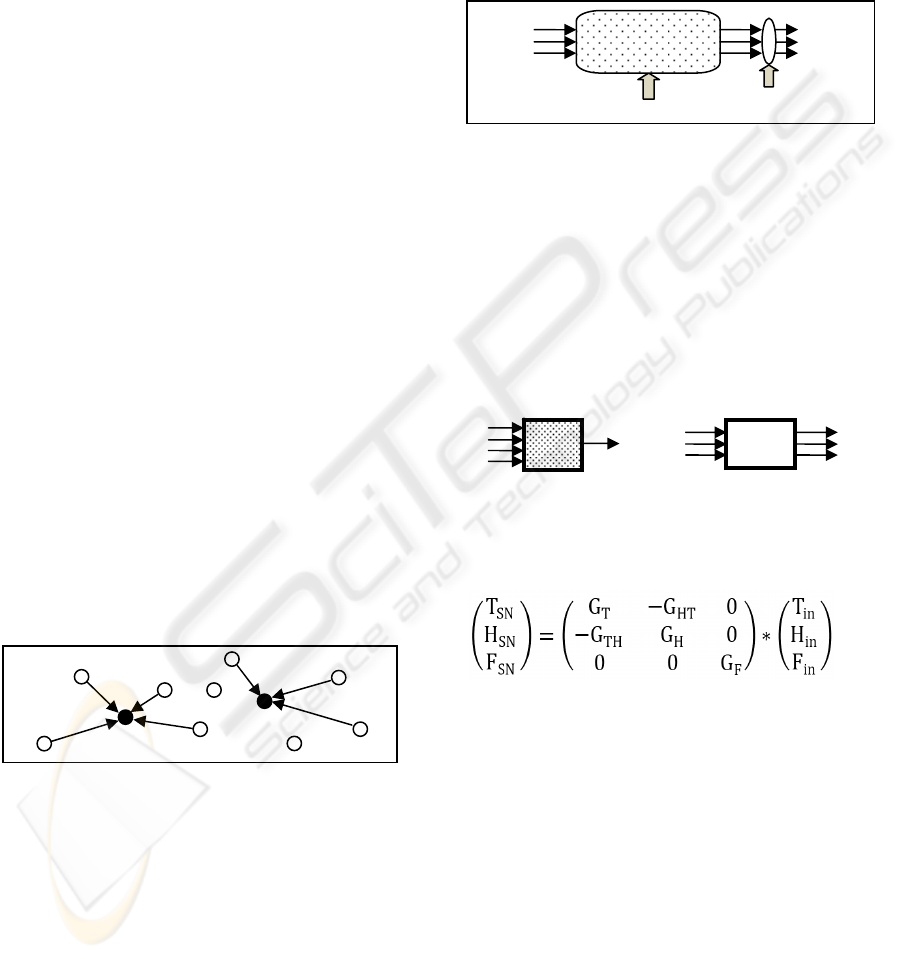
some freight. All attempts in the first step of the

present research are towards introducing a grey-box

nonlinear model between inlet and one DSN. We

will use previous data of a deactivated sensor in

addition to the present and previous data of some

surrounding sensor nodes to estimate unknown

parameters of the related simplified models.

According to fig. 1 and also our main proposal in the

energy management of the wireless sensor network,

there will be a few special key sensor nodes (KSNs)

those will send some specific information to main

processor and or to the other sensor nodes. The

KSNs should be in active mode during the normal

operating mode. The KSNs have three major

functions: (i) they measure environmental conditions

alternatively; (ii) they evaluate measured values and

do some estimation of the ECs in the DSNs and

update previous models after measuring and

receiving some new data; (iii) they will deactivate

DSNs when the operational conditions are normal

and there are no big changes in the ECs. Usually a

while after loading the container, the ECs inside the

container have less variations. This duration is the

best time to utilize the method to take more DSNs to

sleep mode and to estimate the ECS instead of the

direct measurement. The KSNs can be located

everywhere inside the container, even near the door

or near to the inlet. If they are located in some key

points, mismatch error due to no considering

unpredictable phenomenon will be avoidable

because depending on the floating input approach,

uncertainties and disturbances are considered

indirectly as the input change. It is also independent

of the type of the ventilation system. Useful

reference for sensor networks is (

J. Elson, 2004).

Figure 1: Proposed sensor network.

2 PROBLEM FORMULATION

Fig. 2 shows a general scheme of the system, inside

the container between the inlet and a spatial position.

It is a complicate, time and place dependent, multi-

variable system. It consists of three inputs, three

outputs, disturbance and noise. Due to the coupling

in the ECs, doing independent experiments in the

actual container is difficult. It completely depends

on the initial conditions so that a change in the T or

relative humidity of the inlet may change both T and

H in all positions of the space. Variation in the rate

of input air flow changes the measurement results

and disturbance may change all the results so that

based on the existing conditions, measured values

might be different even in the same place.

Figure 2: Schematic of Container as a MIMO model.

Floating input approach identifies multivariable

models between the KSNs and the DSNs, not

between the inlet and a DSN. Every non modeled

disturbances which excite some KSNs, is modeled

as an implicit input change, not a pure disturbance.

Now, the new input nodes (KSNs) in the defined

multi-input and single-output (MISO) system change

output nodes (DSNs). Fig. 3 shows K1, K2, K3 and

K4 as the KSNs and S1 as the DSN.

Figure 3: Models between the KSNs and a DSN.

The first step for modeling is using linear transfer

function matrix. Without considering noise we have:

(1)

, H

and F

) and (T

, H

and F

) are

respectively measured value of (T, H and F) in SN

and inlet. Whereas T and H have opposite effects on

each other, we assign negative sign for the

interconnection. It is assumed that F has no direct

effect on the steady state values of T and H, but it

influences on the speed of their variations. However,

the effect of F are included in all G

, G

and

(which are transfer functions between different

parameters of the ECs) with some exponential

functions that we will mention later. To investigate

validity of the model we employ a reverse lemma

and some assumptions in different border conditions.

Assumption 1, steady state values of T and H:

MISO

{

MIMO

}

Input (inlet):

Temperature

Humidity

Flow

Output (SN):

Temperature

Humidity

Flow

Noise

Disturbance

Multivariable

Syste

A NEW APPROACH FOR MODELING ENVIRONMENTAL CONDITIONS USING SENSOR NETWORKS

It can’t be correct because, negative H can’t be

occurred. We consider some permissible margins so

that T and H locate in the mentioned margin:

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

Having H

min

and H

max

, other input limitations

will be verified. Then there are the specific bands for

inputs so that outputs of linear model will be located

in the admissible areas. Accordant with the lemma,

linear model (1) can’t be a proper model. The

nonlinear model will be made based on the basic

knowledge of the nonlinear nature of the

interconnections. Considering some linear transfer

functions for direct effects and obtained nonlinear

functions for the interactions, we have:

(19)

g(.) and f(.) are nonlinear interconnections

between T and H which are influenced by F. As

stated by

(Ghiaus, 2007) and (Zerihun Desta, 2004),

model of T can be a first-order transfer function. We

also use the effect of the parameters with the same

dimensions in the following:

(20)

(21)

and illustrate speed of the responses and

and M

steady state values of T and H. They

74have reverse relation with F. Then, the further

flow rate, the less

and . The SNs can detecte

variations in the ECs showed by ∆T, ∆H and ∆F.

If the position of the SNs is close, we can assume

that all models in mentioned MISO system, showed

in fig. 3 are independent. It can be considered as

several single-input and single-output (SISO)

systems. Now, they should be combined using a

multivariable identification method. Accordant with

the thermodynamic relations, with 10.1 ºC

increasing T, H will be reduced to the half and we

have:

(22)

(23)

(24)

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

(25)

(26)

(27)

-1

is unit delay in field of Z transform. It is

probable that the amounts of T

oss

and H

oss

are

changed because of the variation in air flow pattern.

However, we consider it on the transfer functions G

and G

when running the on-line estimation. From

previous results, we will derive a time dependent,

nonlinear, multivariable matrix equation and a

function of the several KSNs. Uk is a function to

obtain the effects of the KSNs on a DSN.

(28)

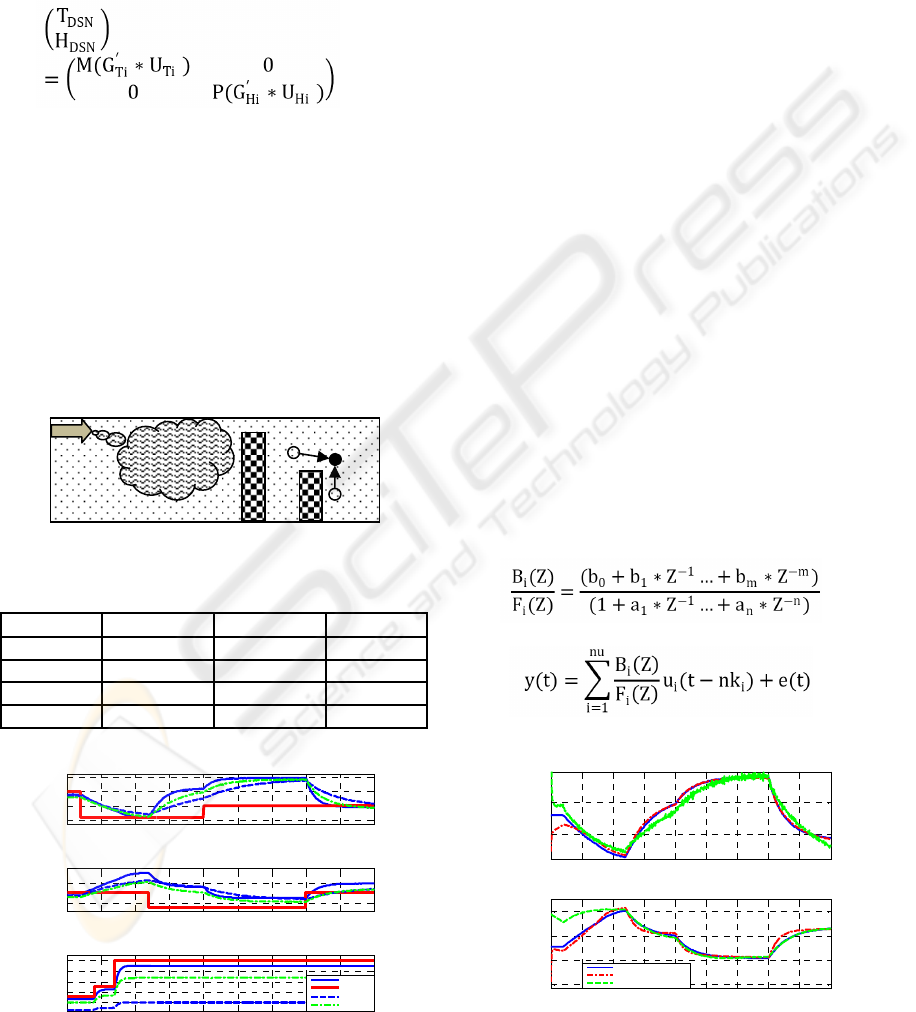
3 SIMULATIONS

Results of the SISO system with initial conditions in

the table 1 has been shown in fig.4. It is noted that a

part of the parameters such as time constant of T in

simulations have been inspired of actual behavior of

a real experiment and the rest are based on primary

assumptions of the authors.

Table 1: Initial conditions for inlet and S1.

inlet 10 30 15

DSN(S1) 9 28.5 13.5

According to fig. 4 Set points of T at 2000, H at

(12000 and 35000) and F at (4000 and 7000)

seconds change. An obstacle as a disturbance

changes the rate of the air flow and influences on the

speed of the responses. However, it will not change

the steady state value of the ECs. The initial

conditions of T and H in output are different with

those in input (inlet) and after changing T in input,

output changes slowly to a new equilibrium point

because the amount of flow is low in the beginning.

At 4000 and 7000 seconds air flow increases

respectively to F

max

/2 and F

max

and immediately the

responses of T and H become faster. When H in inlet

does not change, H in output changes only due to

changing T in output. There is a similar story for T

in output independent of T in input which varies

with the variation of H in output. Dashed curves

show the ECs in a desired place inside the container.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

Temperatures using nonlinear model

Temperature (C)

time (sec)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

Relative Humidities using nonlinear model

R. Humidity (%)

time (sec)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

Air flow using nonlinear model

Flow(m/s)

time (sec)

Sensor

Inlet

Figure 4: ECs in SN when the ECs in input change.

4 AN INDIRECT SOLUTION

We employ the advantages of the sensor network

and introduce floating input approach. We assum

that m numbers of the KSNs are measuring the

conditions when input is inlet and we have:

(29)

(30)

(31)

(32)

(33)

We can suppose that the nonlinear

interconnections from the inlet are both in the KSNs

and the DSNs. Then, we can remove these parts

when we consider the KSNs as the input:

(34)

G´

, G´

are the linear transfer functions

between a KSN and a DSN and its unknown

parameters should be verified using a system

A NEW APPROACH FOR MODELING ENVIRONMENTAL CONDITIONS USING SENSOR NETWORKS

identification technique. Now, we will have some

SISO matrix equations which should to be solved. M

and P are functions for combining linear effects. We

use them in the identification method, indirectly. U

and U

are new inputs, in the m numbers of the

KSNs. G´

and G´

are linear transfer functions of

T and H, written between the KSNs and the DSN.

(35)

5 RESULTS

As an example, showed in fig. 5, there are two KSNs

and one DSN attached to the walls, there are some

obstacles so that the change-rate of the ECs near to

the SNs is different with those in inlet. There are

also different amounts of initial conditions for

different SNs because of their positions or

corresponding measurement errors (table 2). The

simulation results has been shown in fig. 6.

Figure 5: A container with inlet, KSNs and DSN.

Table 2: Initial conditions.

inlet 10 30 15

K1 9 28.5 13.5

K2 8.5 27 3

S1 8 25.5 10

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

a. Temperatures of K1, K2 and S1 using nonlinear model

Temperature (C)

time (sec)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

b. Relative Humidities of K1, K2 and S1 using nonlinear model

R. Humidity (%)

time (sec)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

c. Flows of K1, K2 and S1 using nonlinear model

Flow (m/s)

time (sec)

Source

Figure 6: Outputs when T, H and F in input change.

As shown in fig. 6, curves of K1, K2 and S1 are

according with the data extracted from models

introduced in equations (23) and (26) and curves

related to the inlet are the set points. The relations of

T, H and interconnections are updated based on the

amount of F at the related instant of the simulation.

6 OFF-LINE IDENTIFICATION

Refer to equation (35), there are separate MISO

systems for T as well as H. All unknown parameters

should be determined using an off-line identification

technique. Then, we assume that KSNs are active

and there is a failure on the DSN or it is in sleep

mode and having new inputs we will have the new

estimations of the ECs in the DSNs using existing

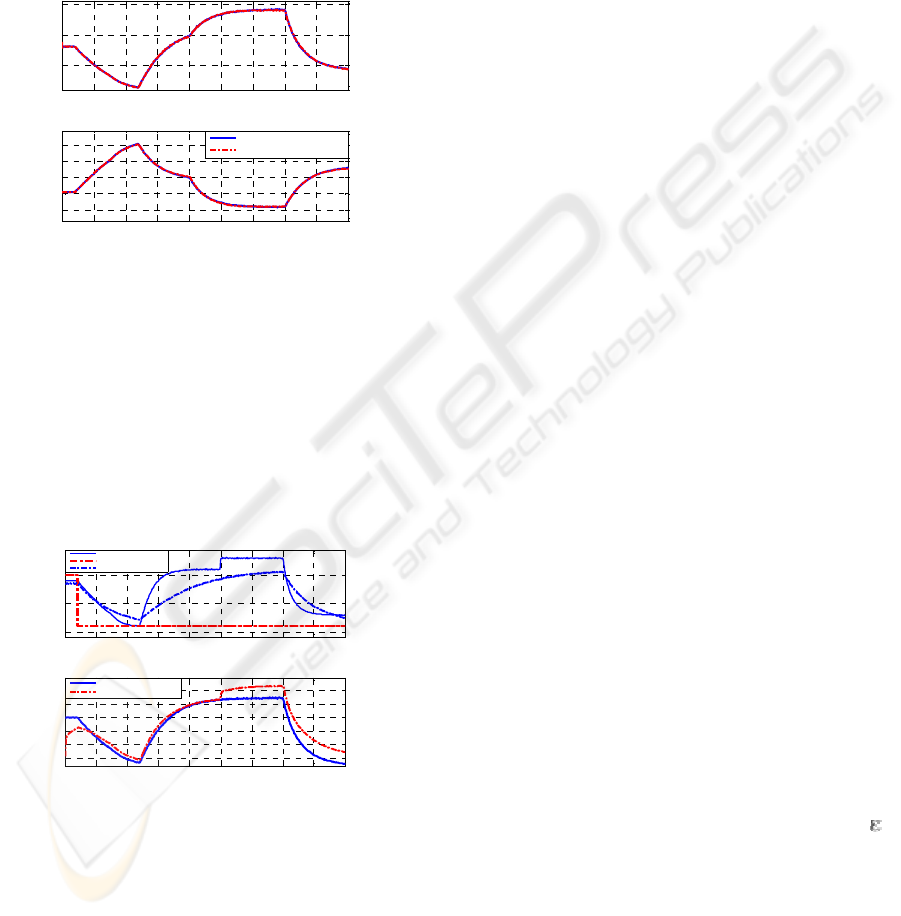
transfer functions. The temperature estimation

results have been shown in fig. 7 and fig. 8 with the

SISO and MISO models, respectively. To show

capability of the method, the results have been

plotted together with the previous results of the EC

in S1 from introduced nonlinear model. the

measured T of K1 in the vicinity of S1, without any

variation in T of inlet and K2. We obtain its effects

on S1 when estimated by K1 and K2 compare with a

regular estimation method using model obtained

from inlet-DSN. The Solid wide curves illustrates

nonlinear model output and dashed curves represent

obtained results separately using linear models and

then with MISO estimation using output error (OE)

method in system identification toolbox of Matlab:

(36)

(37)

0 0.5 1 1.5 2 2. 5 3 3.5 4 4.5

x 10

a. High order SISO Estimation

Temperature (C)

time (sec)

0 0.5 1 1.5 2 2. 5 3 3.5 4 4.5

x 10

b. High order SISO Estimation

R. Humidit y (%)

time (sec)

S1:Actual

S1:Estimate by K1

S1:Estimate by K2

Figure 7: Actual and estimated T and H, model with the

order three using K1 and K2, separately.

Inlet

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

To achieve a desired speed and regard to the

nonlinear nature of the responses that we have still

in the SNs, we utilize a linear transfer function with

the order more than two. Whereas the higher order

models will cause some difficulties in the

application, we don’t use the order more than three.

Separate estimations using SISO models have less

accuracy than those using MISO models.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

c. Multivariable High order model es timation

Temperature (C)

time (sec)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

d. Multivariable High order model estimation

R. Humidity (%)

time (sec)

S1:Actual

S1:High order, Using K1,K2

Figure 8: T and H, actual, estimation using high order

multivariable model from K1, K2.

More important results are obtained when there

is a disturbance in vicinity of the SNs influences

some of the KSNs. fig. 9 shows the variation of T at

25000 seconds which affects both K1 and S1. Model

obtained from inlet-S1 can’t show this influence on

S1 because there are no influences on the inlet.

However, floating input method can estimate it

because at least one KSN senses it.

0 0.5 1 1.5 2 2. 5 3 3.5 4 4.5

x 10

a. Source and measurement results when there is a T disturbance on K1

Temperature (C)

time (sec)

K1: Measurement

T in inlet

K2: Measurement

0 0.5 1 1.5 2 2. 5 3 3.5 4 4.5

x 10

b. Disturbance effects with High order SISO model of K1-S1

Temperature (C)

time (sec)

S1:Estimated by inlet

S1:Estimated by K1

Figure 9: a. measured T in inlet, K1 and K2 and b.

estimation using inlet and K1with existing a disturbanc.

7 CONCLUDING REMARKS

This paper propuses a new hybrid model for

environmental conditions inside a container and

shows that it has much more accuracy for wide

range of parameter variations compared to other

conventional linear models between inlet and a

desired place. The new technique provides a

simplified multivariable model based on the

surrounding sensor nodes used for estimating the

ECs in the desired nodes. The simulation results and

mathematical proofs for different situations endorse

the capability of the proposed technique. At the end,

it should be noted that the comparison among

different multivariable estimation methods and their

implementations as well as finding the minimum

number and the best place of the KSNs are real

challenges main concerns on this issue.

REFERENCES

Ghiaus, C., Chicinas, A. and Inard, C., April 2007, ”Grey-

box identification of air-handling unit elements,

Control Engineering Practice”, Vol.15, Issue 4, pp.

421-433.

Shaikh, N. I and Prabhu, V., May 2007,”Mathematical

modeling and simulation of cryogenic tunnel

freezers”, Journal of Food Engineering, Vol. 80, Issue

2, pp 701-710.

Smale, N.J., Moureh, J. and Cortella, G., Sep. 2006, ”A

review of numerical models of airflow in refrigerated

food applications”, International Journal of

Refrigeration, Vol. 29, Issue 6, pp. 911-930.

Van Brecht, A., Quanten, S., Zerihundesta, T., Van

Buggenhout, S. and Berckmans, D., 20 Jan. 2005,

“Control of the 3-D spatio-temporal distribution of air

temperature”, International Journal of Control, 78:2,

pp. 88- 99.

Zerihun Desta, T., Van Brecht, A., Meyers, J., Baelmans,

M. and Berckmans, D., June 2004, ”Combining CFD

and data-based mechanistic (DBM) modeling

approaches, Energy and Buildings”, Vol. 36, Issue 6,

pp 535-542.

Frausto, H. U. and Jan G. Pieters, Jan.2004, ”Modeling

greenhouse temperature using system identification by

means of neural networks”, Neurocomputing, Vol. 56,

pp.423-428.

J. Moureh and Flick, D., Aug. 2004; ”Airflow pattern and

temperature distribution in a typical refrigerated truck

configuration loaded with pallets”, International

Journal of Refrigeration, V. 27, Issue 5, pp. 464-474.

Rouaud, O. and Havet, M., May 2002, ”Computation of

the airflow in a pilot scale clean room using K-

turbulence models”, International Journal of

Refrigeration, Vol. 25, Issue 3, pp. 351-361.

Sohlberg B., May 2002, Apr. 2003, ”Grey box modeling

for model predictive control of a heating process”,

Journal of Process Control, Vol. 13, Issue 3, pp. 225-

238.

J. Elson and D. Estrin. Sensor Networks: A Bridge to the

Physical World, chapter 1. Wireless Sensor Networks.

Kluwer Academic Publishers, 2004.

A NEW APPROACH FOR MODELING ENVIRONMENTAL CONDITIONS USING SENSOR NETWORKS