DESIGN OF AN ANALOG-DIGITAL PI CONTROLLER WITH

GAIN SCHEDULING FOR LASER TRACKER SYSTEMS

Christian Wachten, Lars Friedrich, Claas Müller, Holger Reinecke

Department of Microsystems Technology, University of Freiburg, Georges-Koehler-Allee 103, 79110 Freiburg, Germany

Christoph Ament

Institue for Automation and Systems Engineering, TU Ilmenau, 98693 Ilmenau, Germany

Keywords: Laser tracker system, PI controller with µC, Analog-digital design, Absolute distance measurement.

Abstract: Laser trackers are important devices in position metrology. A moving reflector is tracked by a laser beam to

determine its position in space. To ensure a proper function of the device the feedback control loop is an es-

sential part. An analog PI controller with online parameter adaptation and absolute distance measurement

ability is used to guarantee an optimal dynamic system. The feedback controller is connected to a quadrant

detector which serves as the sensor element in the control loop. The position of an incoming laser beam is

measured by the quadrant detector and the controller provides the input signals for a subsequent actuator.

The control variable is the deviation of the laser beam from the centre of the diode which should ideally be

zero. The actuator consists of two axes and each one is equipped with a rotatable mirror. The task of the

controller is to rotate the mirrors in such a way so that the laser beam follows the movements of the reflec-

tor. To design an optimal controller linear, time-invariant models of the actuator and the position sensor are

developed to optimize its parameters. The gain of the plant correlates with the distance between the reflector

and the laser tracker. To achieve the optimal dynamic performance the controller is automatically adapted to

the distance during operation. A method based on oscillation injection to measure the absolute distance is

developed. Due to higher dynamic demands a standard analog PI controller is implemented with the con-

troller gain tuned by digital potentiometers. A microcontroller is used to adjust the parameters and to esti-

mate the distance. During the power up sequence and in case of a beam loss the system is completely con-

trolled by the digital part.

1 INTRODUCTION

Laser trackers are devices which are used in position

metrology and in calibration tasks due to their capa-

bility of doing static as well as dynamic high accu-

racy measurements (Riemensperger & Gottwald

1990). A HeNe laser with a Gaussian beam profile

emits two light beams with different frequencies f

and f

. These beams are divided by an interferometer

into a reference beam and a measurement beam. The

measurement beam leaves the interferometer and is

deflected by the mirrors of an actuator in such a

manner that it follows the movement of a retrore-

flector. The reflected light is analyzed by a position

sensitive detector, the analog output signals of which

are used to determine the position of the incoming

beam. The reflected light beam also interferes with

the reference beam in the interferometer. So, by

measuring the two mirror angles of the actuator and

the relative distance given by the interferometer the

position of the reflector is calculated by using an

analytical model. Figure 1 shows the operation prin-

ciple.

An important part of the tracker is the feedback

controller in the tracking unit. It provides the input

signals for the actuator, so that the laser beam fol-

lows the movement of the retroreflector. The basic

task of the controller is to guarantee the proper inter-

ferometer function. Dynamic aspects like a high

velocity or high acceleration of the retroreflector

with a low contouring error are also important.

We present the development of a fast and cost ef-

fective analog feedback controller for a tracking unit

that can be used with laser tracker systems. The

Wachten C., Friedrich L., Müller C., Reinecke H. and Ament C. (2008).

DESIGN OF AN ANALOG-DIGITAL PI CONTROLLER WITH GAIN SCHEDULING FOR LASER TRACKER SYSTEMS.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 5-12

DOI: 10.5220/0001478600050012

 SciTePress

tracking unit is designed for working with an inter-

ferometer but can also act as an autonomous system

because of the integrated absolute distance meas-

urement technique. A distance of about eight meters

between the tracker unit and the reflector is easily

achieved in experiment without static tracking er-

rors. Furthermore, the lateral offset of the laser beam

does not exceed a quarter of the beam diameter and

thus guarantees stable interferometer functionality.

Figure 1: Operation principle of a laser tracker system.

The frequency f

represents the measurement beam and f

the reference beam.

2 SYSTEM COMPONENTS

The tracking unit consists of three components (see

figure 1). The first component is the sensor element

which is a combination of a nonpolarizing beam

splitter and a quadrant diode. The second component

is a x-y scanner with two magnetically driven mir-

rors that deflect the laser beam (galvanometer scan-

ner). The third component is the controller that con-

nects the sensor element with the actuator.

Figure 2: Photograph of the tracking unit. The two mirrors

of the actuator deflect the incoming laser beam. A tilted

mirror is used to adjust the light path.

The laser beam hits a nonpolarizing beam split-

ter. It has a division ratio of 50:50. Afterwards, it is

deflected by the scanner and is then reflected by the

retroreflector. The retroreflector has the unique

property that the incoming laser beam is reflected

into the same direction where it came from. On its

returning path the reflected beam hits the nonpolar-

izing beam splitter again and a part of the beam is

deflected on a quadrant diode. This diode provides

the analog input voltages for the feedback controller

since it has an integrated transimpedance amplifier.

The feedback controller generates the input signals

for the scanner. Ideally, the laser beam is centered

on the diode and the position signals equal zero

volts. By moving the reflector the laser beam leaves

the center on the diode and the position signals

change. The controller compensates the position

change and modifies the input signals of the actua-

tor. The two mirrors rotate and deflect the laser

beam in such a way that the offset becomes zero.

Figure 2 shows a photograph of the complete track-

ing unit.

2.1 Laser Head

The laser is a class II HeNe laser with a Gaussian

beam profile. It emits two linear, orthogonal polar-

ized beams with a split frequency of about 1.8 MHz.

The beam diameter is about 6 mm. The power P of

the laser is about 120 µW.

2.2 Magnetic Actuator

The magnetic actuator is a galvanometer scanner

produced by Cambridge Technology. It has silver

coated mirrors which allow a maximal beam aper-

ture of 10 mm. Each mirror is magnetically driven

and has its own analog PID controller to hold the

desired position. The transfer factor is 0.83 V/° (me-

chanical) at the input side of the controller and

0.5 V/° (mechanical) at the output side of the posi-

tion detector. Integrated sensors allow the measure-

ment of the rotation angle of the mirrors. The short

term stability is about 8 µrad. The maximal me-

chanical rotation angle is ± 12.5° limited by the used

assembly.

2.3 Quadrant Photodetector

The sensor element of the tracking unit is a quadrant

photodiode. Figure 3 shows a photograph of the pho-

todiode and a sketch of its quadrants. Each quadrant

is sensitive to light with a sensitivity that is specified

to 0.54 A/W at a wavelength of 900 nm. The spacing

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

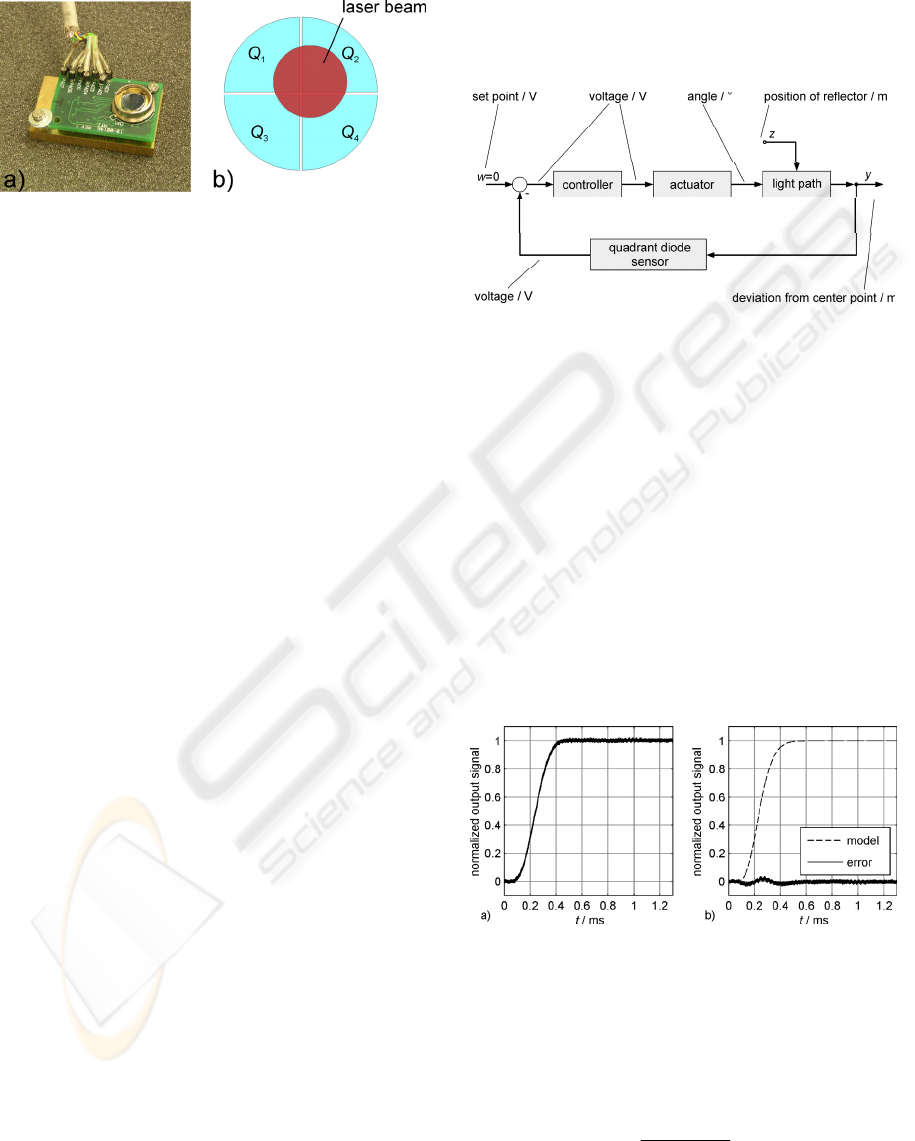
between the quadrants is 0.2 mm, the quadrant ra-

dius is 3.99 mm.

Figure 3: Photograph of the quadrant detector a) and

sketch b) of its quadrants. The voltage level of the position

signals depends on the area that is covered by the laser

beam, its shape, its power and the wavelength.

The diode current depends on the power of the

laser beam, its shape, its wavelength and the area

that is covered. To perform a current to voltage

transformation a transimpedance amplifier is put on

the same circuit. The output of the amplifier consists

of three voltages that completely define the position

and the power of the laser beam. The signals can be

calculated with the following formulas:

4321

10)( ⋅+++= IIIIV

Sum

V/A (1)

4321

10))()(( ⋅+−+= IIIIV

V/A (2)

4231

10))()(( ⋅+−+= IIIIV

V/A (3)

The symbol I

represents the current of a quad-

rant Q

. The signal V

Sum

is the summation of the

voltages that are generated by each quadrant and

thus is an indicator for the total power of the incom-

ing light beam at a known wavelength. The signal

, the so called top-bottom voltage, represents the

position of the laser beam in vertical direction. The

signal V

, the so called left-right voltage, represents

the position of the laser beam in horizontal direction.

If for example the laser power is the same on each

quadrant, V

and V

become zero volts.

3 MODELING OF THE PLANT

A block diagram of the system is shown in fig-ure 4.

The output signal y of the system is the deviation of

the light beam from the center of the quadrant diode.

This deviation should become zero for each compo-

nent. The output signal y is a superposition of the

movement of the reflector and the compensation part

of the actuator. The gain between the mirror angle

and the movement of the light beam on the diode

depends on the distance between the reflector and

the tracking unit. This is modeled in the block “light

path”. The symbol z represents the position of the

reflector in space and thus is a three-dimensional

vector. The signal y represents the beam position on

the diode area and thus is a two-dimensional vector.

Figure 4: Block diagram of the plant. The different inputs

and outputs with their units are shown.

To design an optimal feedback controller, mod-

els are developed and the model parameters are

identified for the blocks “actuator”, “quadrant di-

ode” and “light path”.

3.1 Modeling of the Block “actuator”

To obtain a transfer function for the magnetic actua-

tor the step response is recorded for each axis moni-

toring the position output of the integrated angle

encoders. A square wave with a peak-peak voltage

of 100 mV (corresponding to an angle of about

0.06°) and a frequency of 30 Hz is applied to the

inputs of the scanner.

Figure 5: Normalized and averaged measurement a) of the

step response of the y mirror and the model b) of the step

response with its error. The step rises at t = 0 s.

Figure 5 shows the measured step response and

the step response of the model for the y mirror. It is

assumed that the scanner has PT

behavior and thus

can be modeled with a PT

element in (4).

)1(

)(

⋅+

, i = x,y (4)

DESIGN OF AN ANALOG-DIGITAL PI CONTROLLER WITH GAIN SCHEDULING FOR LASER TRACKER

SYSTEMS

The parameter K

describes the gain and the pa-

rameter T

represents the time constant for axis i.

The parameter n

stands for the order of the element.

To obtain the parameters the method of the time

percentage values is applied. Since the measurement

is not supposed to have ideal PT

behavior a least-

squares fit is done to optimize the parameters so that

the error between the model and the measurement

becomes minimal. The start parameters for the opti-

mization are the results given by the method of the

time percentage values (Schwarze 1962). The final

optimization yields in n

= 9 and T

= 27.51 µs for

the y mirror. The parameters for the x mirror result

in n

= 10 and T

= 23.42 µs. Taking into account

that the gain between the output signal and the me-

chanical deflection is 0.5 V/° the gains are calculated

to K

= 1.210 °/V and K

= 1.207 °/V, respectively.

The -3 dB frequency is about 1.8 kHz (model).

3.2 Modeling of the Block “diode”

The time response of the diode can be modeled in

the same way as the time response for the actuator.

A red LED is used to generate the step response be-

cause it is fast enough and its time response can be

neglected. The output signal V

Sum

is measured. The

LED has a power of about 7 µW. Figure 6 shows the

measurement and the model of the step response.

Figure 6: Normalized and averaged measurement a) of the

step response of the diode and the model b) with its error.

A red, pulsed LED is used to illuminate the active area.

The step rises at t = 0 s.

The modeling with only a single PT

element is

not applicable because there is a steep increase of

the signal until 1.6 µs. Afterwards, the signal in-

creases very slowly and does not reach 100% even

after 4 µs. Therefore, it can be shown that a good

approximation is a combination of a PT

element

and a PT

element. This is done in (5).

⋅+

−

⋅+

)1(

)(

(5)

The parameters T

and T

represent time con-

stants of the two elements, the parameter g normal-

izes the output and the parameter n

represents the

order of the PT

element. All parameters are ob-

tained using a least squares fit so that the deviation

of the model and the measurement becomes mini-

mal. The optimal parameters are n

= 7, T

= 136 ns,

= 4.75 µs, g = 0.793. The model predicts a -3 dB

frequency of 250 kHz.

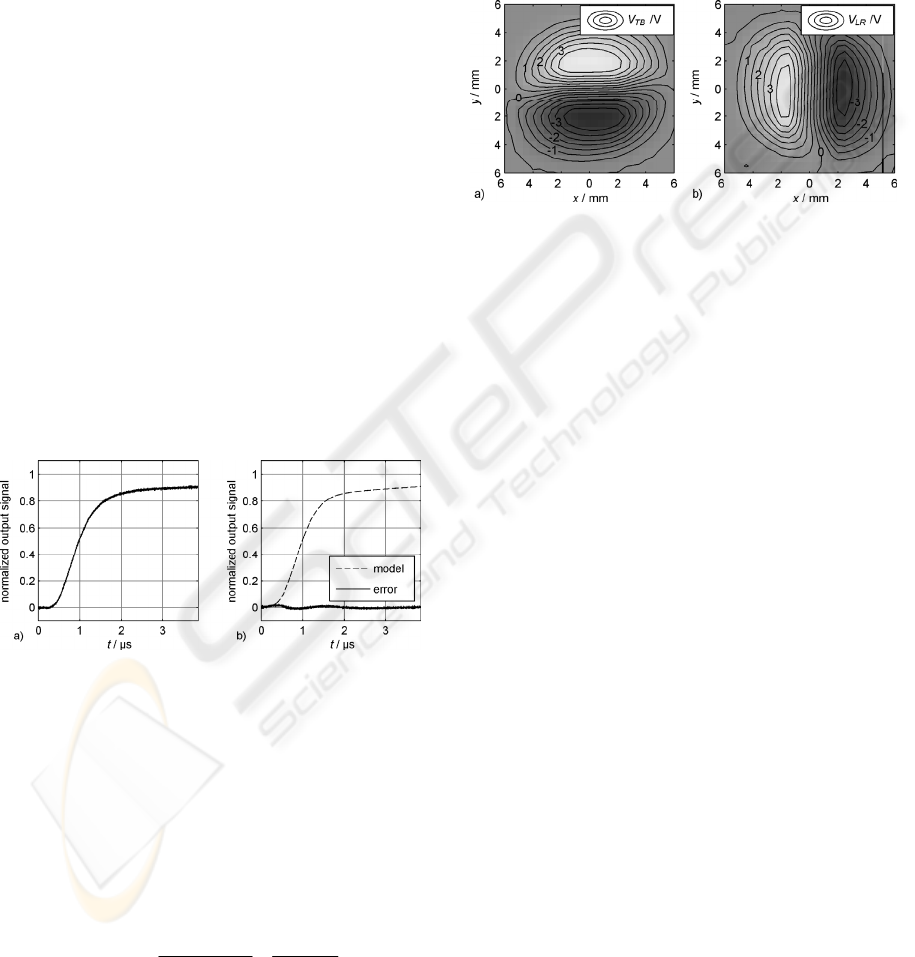
Figure 7: Local behavior of the diode. There is a nonlinear

relation between the output voltage and the position of the

beam.

Because the diode generates position signals not

only the time response is important but also its local

behavior. Figure 7 shows the local behavior of di-

ode. The quadrant diode was put onto an x-y station

and a laser diode with a power of 771 µW was in-

stalled in front of it. The station moves to 900 de-

fined positions that are placed in an equally spaced

square.

In figure 7 it can be seen that there is a nonlinear

relation between the position and the output volt-

ages. In the center of the diode the contour lines are

nearly parallel to the corresponding axis and so a

linearization is possible. It is obvious that the signal

only depends on a movement in y direction and

only depends on a movement in x direction. As a

result, each axis of the scanner can be regarded as

independent.

3.3 Modeling of the Block “light path”

The block “light path” depends on the position of the

reflector. If the angular errors are neglected the re-

flector can be approximated as its center point in a

plane (see figure 8a). The hitting point of the incom-

ing laser beam is point reflected with the center. An

offset between the incoming and the reflected laser

beam can have different reasons, for example a rota-

tion or a lateral displacement of the reflector.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

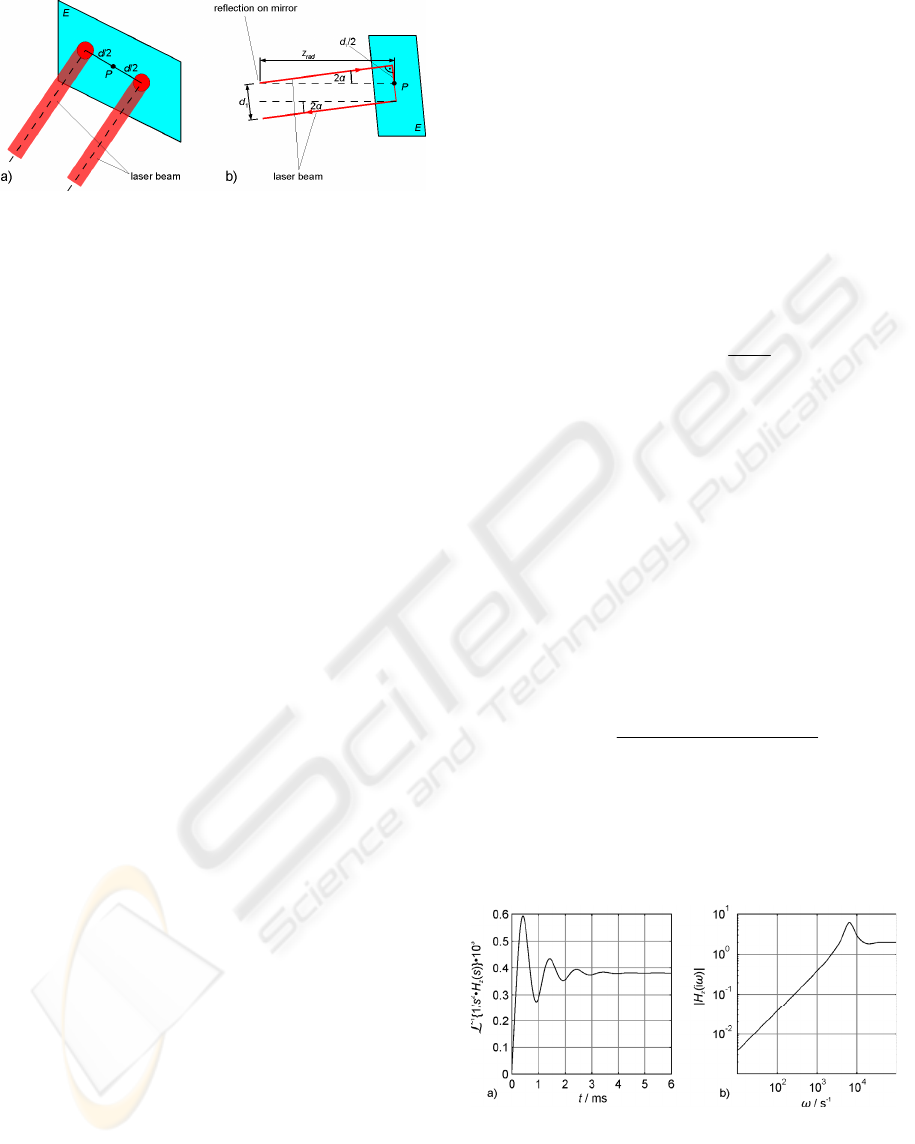
Figure 8: Modeling of the reflector. An incoming beam is

reflected at the center of the reflector.

The first effect is shown in figure 8b. The mirror

rotation angle is α. It is assumed that the reflector is

rad

away from the tracking unit. So the offset d

can

be written as

⋅⋅≈⋅⋅=

radrad

zzd 4)2sin(2

(6)

The second effect resulting in a beam offset is

the lateral displacement z

lat

of the reflector. The in-

dices represent the coordinate frame of the diode. So

it can be written as

ilati

,,2

2 ⋅= , i = x,y (7)

The total deflection on the quadrant diode is a

combination of these two effects as shown in (8)

ddy

,21

+= , i = x,y. (8)

4 CONTROLLER DESIGN

The controller has to be designed separately for the x

and the y-axis. Because of the decoupling of the

axes shown in figure 7 the problem is reduced to the

controller design for one axis. Exemplarily, the x-

axis is used to demonstrate the design process. It can

be derived from the block “light path” that the gain

of the plant correlates with the distance z

rad

. In a first

step it is assumed that z

rad

is constant. During opera-

tion the controller should be automatically adapted

to the distance so the restriction z

rad

= const. is

dropped. This adaptation to the distance is known as

gain scheduling.

The controller has to fulfill several requirements

for the use in laser tracker systems. First, the offset

of the beam should be smaller then a quarter of the

beam diameter to guarantee the interferometer func-

tion. Second, a high velocity of the reflector is nec-

essary to allow rapid movements of the object. The

third requirement is the robustness against vibrations

without any disturbance of the measurement accu-

racy. Of course, a large measurement volume is de-

sirable, too.

To achieve stationary accuracy the controller

should possess an integrating part because the plant

only consists of proportional blocks. A pure I con-

troller is also possible but a proportional part en-

hances the performance (Merz & Jaschek 1996). A

PI controller is well suited for plants with PT

be-

havior.

A standard PI controller is proposed due to its

simple design and to reduce the analog circuit com-

plexity because the derivative part is missing. The

transfer function is well known and given in (9).

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+⋅=

KsH

1)(

(9)

The parameter K

describes the gain of the con-

troller and T

its time constant. First, these parame-

ters are determined by the classic frequency re-

sponse method as described by Föllinger (1994).

The time constant T

is set to T

= 23.42 µs because

this is the dominating time constant of the x mirror

in the plant. The gain K

R,30°

is set to 0.1231 to obtain

a phase margin of 30° for the gain crossover fre-

quency. It is of interest to examine the disturbance

transfer function because the set point (w(t) = 0) is

constant. H

(s) is calculated in (10) and is derived

from the block diagram in figure 4.

)()()(1

)(

sHsHsH

DRS

⋅⋅+

(10)

To estimate the performance of the classic feed-

back controller the response to a ramp in z

lat,i

and the

magnification factor is simulated for the disturbance

transfer function in (10).

Figure 9: Simulation of the ramp response a) and the fre-

quency response b) of the disturbance transfer function

with a classic PI controller.

A ramp is chosen because it is the strongest re-

quirement concerning the reflector movement. A

DESIGN OF AN ANALOG-DIGITAL PI CONTROLLER WITH GAIN SCHEDULING FOR LASER TRACKER

SYSTEMS

step is not applicable because in reality the position

of the retroreflector cannot rapidly change.

Figure 9a) shows the response on a ramp in z

lat

(t)

at the output y

of the system. The maximal value of

the overshoot at the output y

is 0.60·10

-3

m until a

constant contouring error of 0.38·10

-3

m is reached.

Figure 9b) shows the frequency response. Low fre-

quencies are damped due to the integrating part. But

there is a magnification factor of 6.3 at a frequency

of 1 kHz.

The maximal value is reached at the overshoot,

but the contouring error is much lower. Therefore,

the maximum of the ramp response has to be mini-

mized so that the overshoot is reduced at the cost of

the contouring error. The aim is the adaptation of the

overshoot to the contouring error. For ω→∞,

(iω)| converges to 2, so an arbitrary factor of 4 is

proposed for all frequencies to guarantee robustness

against vibrations. To identify the optimal controller

parameters K

and T

were varied in a range of

= 0.1·K

R,30°

…10·K

R,30°

and T

= 0.1·T

…10·T

The raster was ΔK

= 0.05·K

R,30°

and ΔT

= 0.05·T

Figure 10 shows the ramp response and frequency

response for the optimized parameters K

R,opt

= 0.542

and T

R,opt

= 135 µs. The maximal value of the re-

sponse is about 0.51·10

-3

m with a very low over-

shoot and the magnification factor does not exceed

4. So, the quality of control is much better in com-

parison with the classic approach.

Figure 10: Simulation of the ramp response a) and the

frequency response b) of the disturbance transfer function

with optimal controller parameters in regard to contouring

error and magnification factor.

It was assumed that the total gain is focused in

the parameter K

. This is not the case in a real sys-

tem. The real total gain is a product of the controller

gain, the mirror gain, the light path and the sensitiv-

ity of the quadrant diode. It can be written as

DradxRoptR

KzKKK ⋅⋅⋅⋅= 4

(11)

Dradx

optR

KzK

⋅⋅⋅

=⇔

(12)

To adapt the controller gain, the parameters K

and K

have to be updated during operation (gain

scheduling). The parameter K

is obtained by meas-

uring the voltage V

Sum

of the quadrant diode. The

parameter z

rad

has to be estimated.

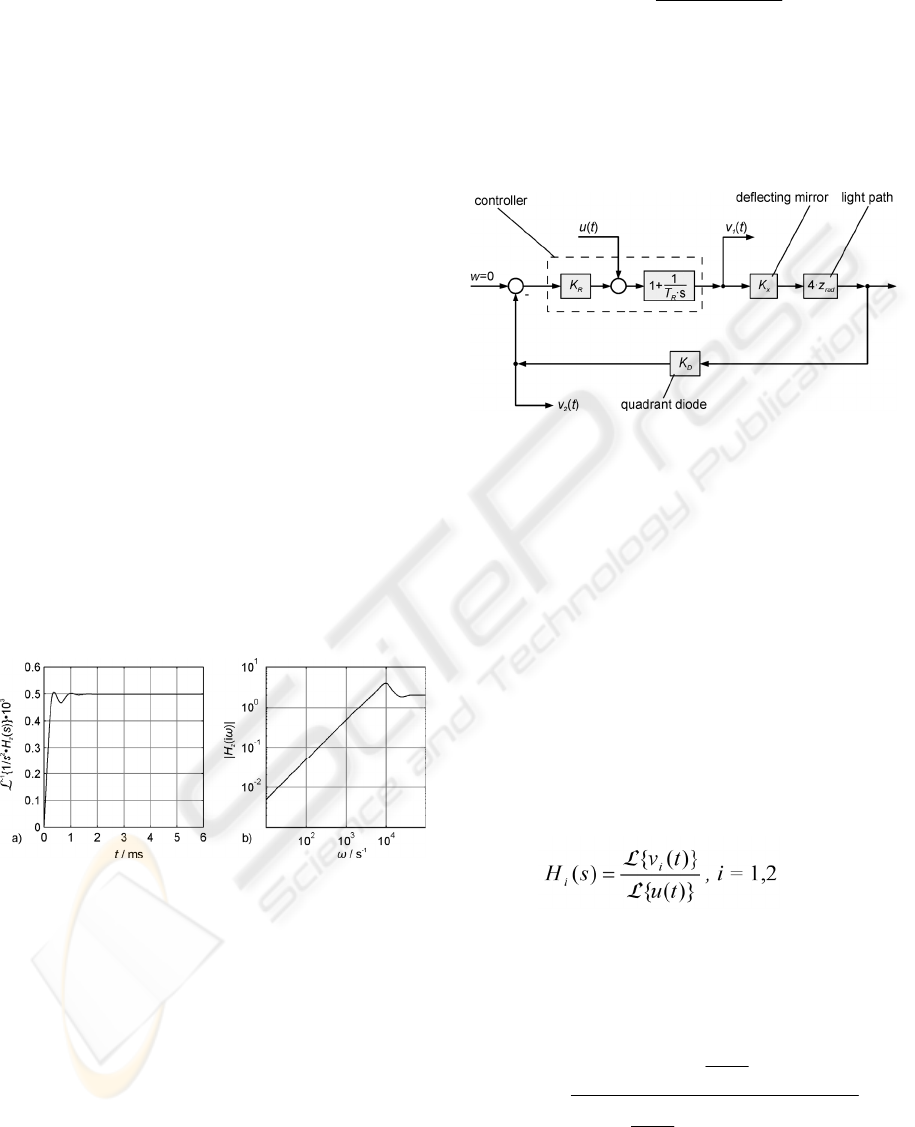
Figure 11: Control loop with introduced signal u(t) to es-

timate z

rad

. The signals v

(t) and v

(t) can be measured and

depend on z

rad

To estimate z

rad

a known signal u(t) is introduced

into the control loop (figure 11). Only the spectral

components are considered which are below the cut-

off frequency of the diode. So, it is possible to sim-

plify the transfer functions and consider only their

proportional parts. But the time response of the con-

troller cannot be neglected because there is a strong

dependency on low frequencies introduced by the

integrating part. The multiplication with z

rad

is mod-

eled as proportional part because z

rad

changes slowly

in comparison to the system dynamic.

The signals v

(t) and v

(t) depend on the distance

rad

. The transfer functions can be calculated with

(13).

(13)

It can be shown that there is a higher sensitivity

|)(|

iH to a change in z

rad

if signal v

(t) is

measured. With (13) and figure 11 the transfer func-

tion H

(s) is calculated in (14).

xradDR

KzKK

⋅⋅⋅⋅⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

)(

(14)

The signal v

(t) is a superposition of the movement

of the reflector and the introduced signal u(t). A si-

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

nusoidal signal with a frequency ω

is proposed. So,

a subsequent band-pass filter with the center fre-

quency ω

suppresses the disturbance signal intro-

duced by the reflector. To estimate the distance z

rad

the amplitude of u(t) is compared with the amplitude

(t) and so |H

(iω)| is calculated. With the experi-

mentally obtained relationship for K

in (15), z

rad

calculated in (16). The proportional value m has a

value of 45.13 V

-1

Sum

⋅

(15)

(

))2(1(

222

ωω

RRrad

TTAAz +−−= (16)

)

(

)

)1(/

222

ωω

RSumRR

TmVKATA +−

with

|)(|

iHA = .

To obtain an appropriate value for the amplitude

of the signal u(t) the beam deviation y

(t) from the

center of the quadrant diode is analyzed. The devia-

tion should be smaller than a quarter of the beam

diameter to guarantee the interferometer function.

During distance estimation the deviation y

(t) is a

superposition of the lateral movement of the reflec-

tor z

lat,x

(t) and the introduced signal u(t). Therefore,

the amplitude of the signal u(t) is chosen to be only

10% of the maximal deflection so that the maximal

velocity v

lat

is not reduced. With the transfer func-

tion H

(s) and a maximal amplitude y

x,max

of y

(t) the

amplitude u

is calculated in (17).

|)(|

max,0

⋅=

(17)

Because z

rad

is located in the denominator of (17)

its increase leads to a decreasing amplitude u

. Ac-

cording to the described limit of 10%, y

x,max

is set to

R/20 with R being the radius of the beam.

5 PRACTICAL

CONSIDERATIONS

The feedback controller is implemented in an analog

design. To generate the signal u(t), to measure the

signal v

(t) and to adapt the gain of the controller, a

microcontroller is used. The microcontroller is an

ATmega128 and is programmed in C. The variable

gain control is realized by digital potentiometers that

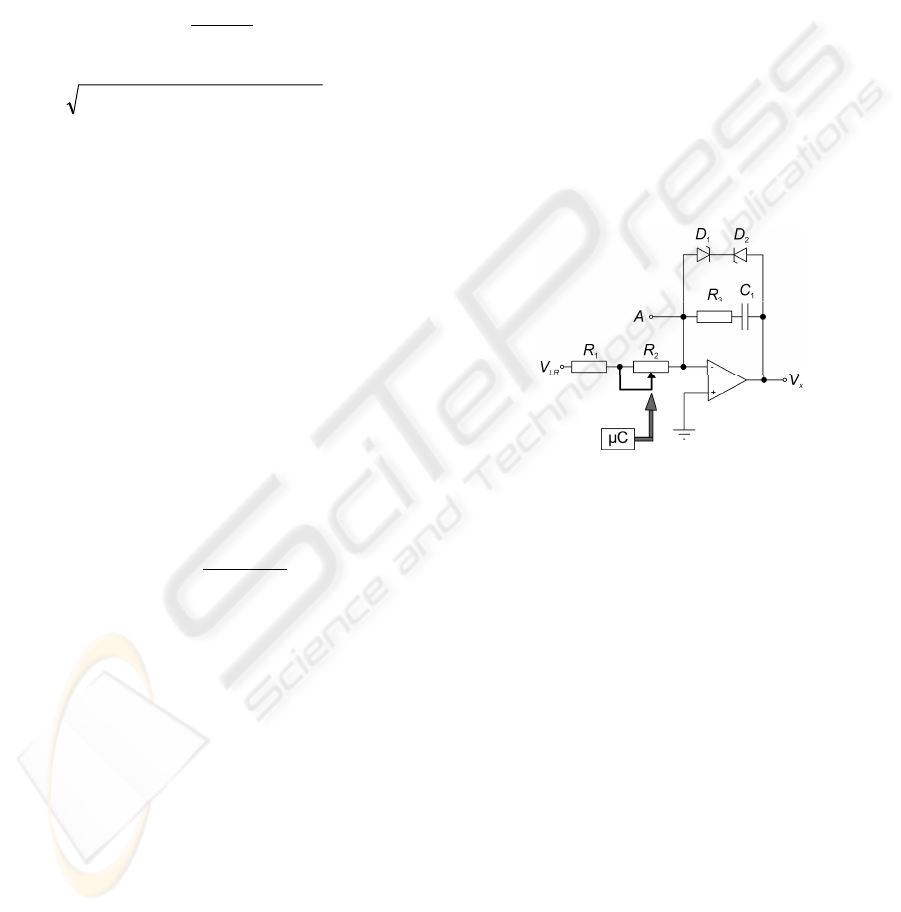
are set by the microcontroller. Figure 12 shows the

used circuit for one axis. The digital potentiometer

offers 127 linearly arranged steps. The resistance

can be adjusted between 1 kΩ and 50 kΩ.

The analog PI controller is built with standard

components without complex serial or parallel circi-

uts resulting in a time constant of T

= 132 µs and a

adjustable gain between K

= 6.00·10

-3

… 300·10

-3

The parameter T

remains constant even if the po-

tentiometers change their value. Because of the dis-

crete potentiometer positions there is an error be-

tween the optimal controller gain and the achieved

controller gain. There are only integer positions n

int

available. To obtain an optimal value for K

the

theoretical real number n

real

for the potentiometer

position is calculated. Afterwards, n

real

is rounded

down and up and the lower and the upper controller

gains K

and K

are calculated. The controller gain

with the minimal error in regard to the optimal value

is chosen.

Figure 12: Microcontroller controlling a digital potenti-

ometer and analog PI controller exemplarily shown for the

x-axis.

After power up sequence and beam loss during

operation, the laser beam searches the reflector in a

defined area. This is done by deflecting the mirrors

of the actuator without opening the feedback loop.

The influence of the analog part is reduced and only

the digital part controls the mirror deflection.

Figure 13 shows the operation principle. The

digital potentiometer is set to its maximal value. So,

the influence of the sensor signal to the input of the

PI controller is weak. This is comparable to an open-

ing of the feedback loop and the signal can be cross

talked easily.

The microcontroller introduces a signal at the in-

put of the PI controller. At the same time the re-

duced sensor signal of the diode acts as a distur-

bance variable. The output of the controller is digi-

talized and is compared to the set up variable w

The microcontroller multiplies the gain K

with the

deviation e. So, the plant with integrating behavior is

controlled via a P controller which is a good combi-

DESIGN OF AN ANALOG-DIGITAL PI CONTROLLER WITH GAIN SCHEDULING FOR LASER TRACKER

SYSTEMS

nation (Merz & Jaschek 1996). The DA conversion

at the output of the microcontroller is done via a

pulse width modulation (PWM) with a frequency of

14.4 kHz and a low-pass filter with a cut-off fre-

quency of 300 Hz (smoothing function).

Figure 13: Operation principle for deflecting the mirrors in

a defined way.

The output of the controller is digitized by the in-

tegrated AD converter of the microcontroller. To

reduce alias effects a low-pass filter with a cut-off

frequency of 300 Hz is used, too.

represents the total gain of the control loop

and is set to K

= 41. This is a tenth of the value of

the stability limit. So, the safety margin is high

enough to avoid instability.

Figure 14: Estimated z’

rad

as a function of the real z

rad

Each point is averaged 20 times with its two-time standard

deviation. To increase readability the measurements for

= 0.3 show a horizontal offset of -0.02 m and for

= 0.17 an offset of +0.02 m.

To estimate the distance z

rad

between the system

and the retroreflector a signal is introduced in the x-

axis (figure 11). To reduce the computing and pro-

gramming complexity a square wave with a fre-

quency of 200 Hz instead of a sinusoidal signal is

used. An analog band pass filter with the same fre-

quency is used for signal pre-processing. Only the

basic frequency is considered in the signal analysis.

Because the movement of the retroreflector has only

few spectral components in the pass-band the gain

can be increased without leaving the input range of

the AD converter. So, a small value of u

is suffi-

cient to detect the amplitude of v

(t) with a DTFT.

Figure 14 shows the distance estimation for dif-

ferent gains of the controller. To reduce the time

effort only distances between 0.5 m and 2.3 m are

measured. The estimated value shows a good accor-

dance to the real values. The variance increases with

the distance because of the reduced sensitivity of the

measured voltage to the distance.

Further experiments have shown that the retrore-

flector can be moved with a maximal velocity of

max

= 2.5 m/s at unlimited acceleration and a beam

offset of a quarter of the beam diameter. Distances

between 0.5 m and 7.8 m (length of laboratory) were

tested without tracking problems.

6 CONCLUSIONS

An analog PI controller with additional features was

presented for the use in laser tracker systems. It is

fast to detect a rapid beam movement and shows

good control accuracy. Functions as gain scheduling

and distance estimation are integrated in this hybrid

design consisting of a digital and analog part.

REFERENCES

Föllinger, O., 1994. Regelungstechnik. 8

ed. Heidelberg:

Hüthig GmbH.

Merz, L. & Jaschek, H., 1996. Grundkurs der

Regelungstechnik. 13

ed. München/Wien: R.

Oldenburg Verlag.

Riemensperger, M. & Gottwald, R., 1990. Kern Smart 310

– Leica’s Approach to High Precision 3D Coordinate

Determination, In: F. Löffler, 2

International Work-

shop on Accelerator Alignment. Hamburg, Germany,

10-12 September 1990. pp. 183-200.

Schwarze, G., 1962. Bestimmung der

regelungstechnischen Kennwerte von P-Gliedern aus

der Übertragungsfunktion ohne

Wendetangentenkonstruktion, Messen, Steuern,

Regeln, 5, pp. 447-449.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics