A DYNAMIC MODEL OF A BUOYANCY SYSTEM IN A WAVE

ENERGY POWER PLANT

Tom S. Pedersen and Kirsten M. Nielsen

Department of Automation and Control

Aalborg University, Fr. Bajersvej 7, Aalborg, Denmark

Keywords: Dynamic model, wave energy, simulation, buoyancy control, verification, renewable energy.

Abstract: A nonlinear dynamic model of the buoyancy system in a wave energy power plant is presented. The plant

(“Wave Dragon”) is a floating device using the potential energy in overtopping waves to produce power. A

water reservoir is placed on top of the WD, and hydro turbines lead the water to the sea producing electrical

power. Through air chambers it is possible to control the level, the trim and the heel of the WD. It is

important to control the level (and trim, heel) of the WD in order to maximize the power production in

proportion to the wave height, here the amount of overtopping water and the amount of potential energy is

conflicting. Five separate air chambers, all open to the sea, makes the device float. The pressures in the air

chambers may be individually controlled by an air fan through an array of valves. In order to make a model-

based control system, this paper presents a model describing the dynamics from the air inlet to the level,

trim and heel. The model is derived from first principles and is characterized by physical parameters.

Results from validation of the model against plant data are presented.

1 INTRODUCTION

Renewable energy is an important issue due to the

global warming problem and utilisation of wave

power is one of the energy resources to be exploited.

The wave power system “Wave Dragon”, on

which this paper focuses, was invented by Erik Friis

Madsen, Löwenmark and tested at Aalborg

University and University of Cork. An EU based

European consortium has been involved in the

construction and implementation of a 1:4 scaled test

site - 57x27 m wide and with a weight of 237

tonnes- which is placed in Nissum Bredning in

Denmark. Large numbers of tests have been carried

out during a two years operating period. One goal

for energy production improvement is a better

control of the Wave Dragon buoyancy.

Wave Dragon (WD) is an offshore wave energy

converter of the overtopping type, a description is

found in (Kofoed, 2006) and (W.D.Aps, 2006). The

main structure consists of a ramp where the waves

are overtopping and led to a reservoir (basin). Two

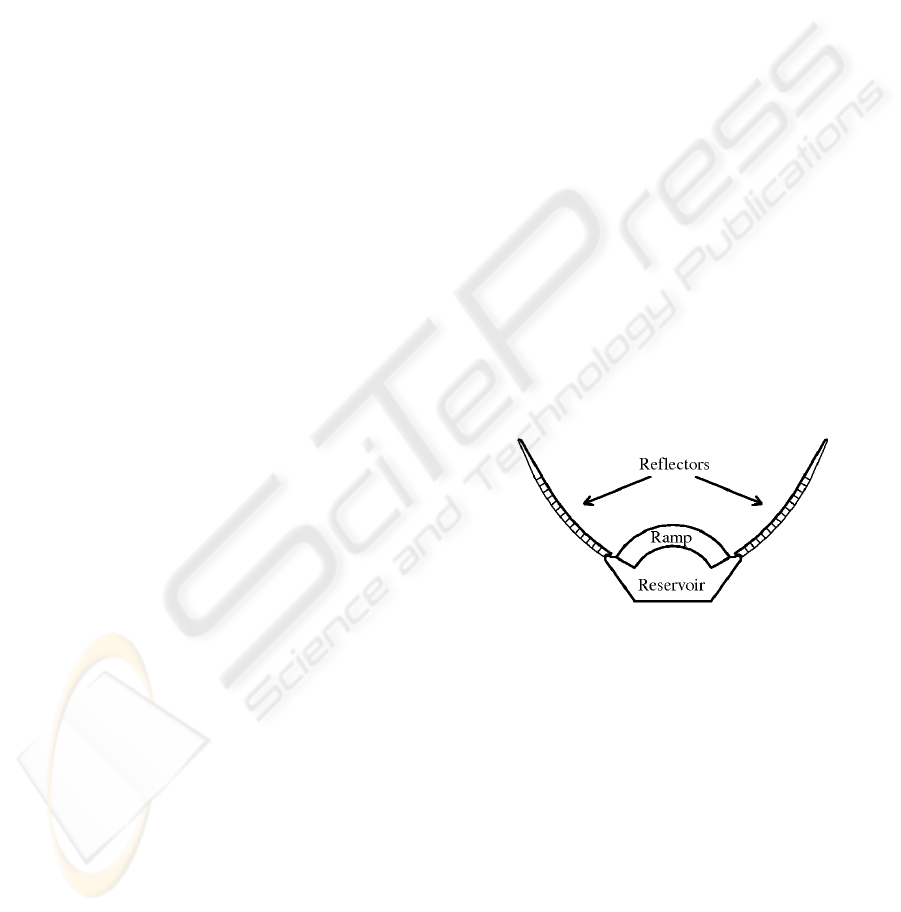
reflectors are focusing the waves towards the ramp

as seen on figure 1. WD is fastened to an anchor

making it possible to turn the ramp towards the

dominant wave direction.

Figure 1: Main components of the Wave Dragon (Kofoed,

2006).

The WD use the potential energy of the waves,

meaning that for a given wave type there exist an

optimal level of the reservoir. As shown on figure 2

the reservoir water is led through a turbine.

The WD floats on open air chambers used to

adjust the floating level. Control of the floating level

is a part of optimizing the overtopping and a

dynamic model for a model-based control system is

the topic of this paper. It should be noted that the

wave conditions are measured online and may be

used as reference to the level control system.

First the wave dragon buoyancy system is

presented. A dynamic model of the air supply system

controlling the pressure in the air chambers is set up.

S. Pedersen T. and M. Nielsen K. (2008).

A DYNAMIC MODEL OF A BUOYANCY SYSTEM IN A WAVE ENERGY POWER PLANT.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 13-17

DOI: 10.5220/0001479200130017

 SciTePress

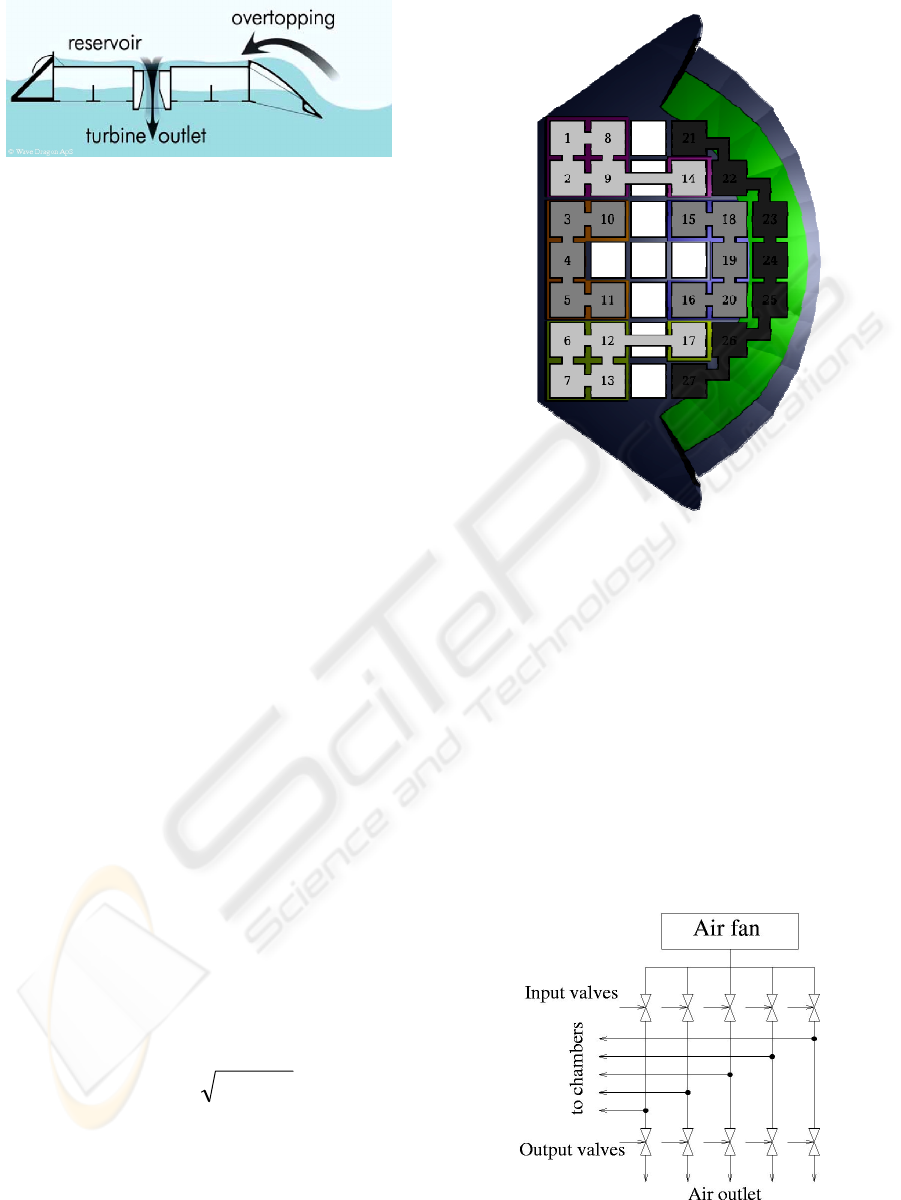
Figure 2: The basic principle of WD showing waves

loading the reservoir via the ramp. (Kofoed, 2006).

The model parameters have been adjusted to the test

site Wave Dragon. Finally the buoyancy model is

verified by comparing simulation results and

measurements from the test site Wave Dragon.

2 DYNAMIC MODEL OF THE

BUOYANCY SYSTEM

The buoyancy system consists of five air chambers

all open to the water surface. The five chambers are

shown on figure 3 (21,22,23,24,25,26,27),

(15,16,18,19,20), (3,4,5,10,11), (1,2,8,9,14) and

(6,7,12,13,17). Furthermore 9 small chambers

contain a constant amount of air.

The air pressures in the chambers are controlled

by an air supply system using an on/off driven air

fan and input/output valves to each chamber. The

valves are operated as on/off valves and only one

valve is allowed to be active at the time in order to

prevent pressure equalizing in the chambers. A

PWM scheme is in (Andersen, 2007) proposed to

handle this problem. The air supply system model

consist of two parts, one describing air inlet to the

chamber and one describing air flow out of the

chamber. In both models tube pressure drops are

ignored. The inlet air mass flow, m

ai,

is given by

pbacpaai

KppKm +−−= )(

which is an approximation to the fan characteristic.

is the chamber pressure, p

is the inlet pressure to

the fan (atmospheric pressure) and the two

constants K

, K

are from the fan data sheet.

Air outlet mass flow, m

ao,

is given by the

Bernoulli equation:

acvoao

ppKm −=

where the constant K

depend on the outlet tube

dimension and the air density.

Each input/output valve pair is controlled by a signal

u, where u=1 allows an airflow into the chamber,

u=0 closes both valves and u=-1 open the outlet

valve. This gives the air mass flow equation:

Figure 3: The air chambers in the Wave Dragon.

)()(

ugmugmm

aoaia

−

(1)

where

⎩

⎨

⎧

≥

)(

uif

⎩

⎨

⎧

−>

−≤

)(

uif

Eq. (1) describes the air mass flow to the chamber

and is valid when only one chamber is operated at a

time.

Figure 4: Fan/valve system.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

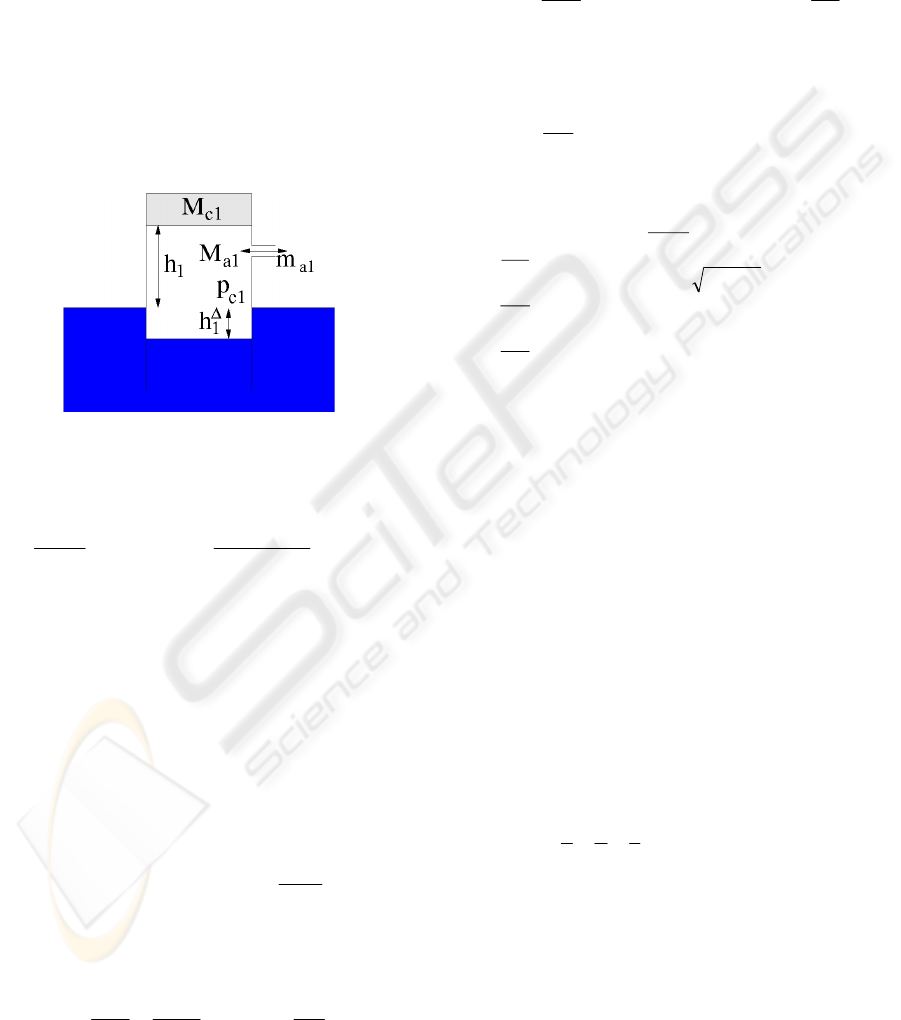
3 ONE CHAMBER DYNAMIC

MODEL

This section outlines the dynamic describing

equations for a single chamber. The equations

assumes that the air density is constant (variations

could be included using the ideal gas equation), the

chamber is only moving along a vertical axis

perpendicular to the water surface, the cross section

area is constant along this axis and there is only one

rigid moving body. The model then consists of a

mass balance equation describing the air in the

chamber and a Newton equation describing the

motion of the chamber.

Figure 5: One chamber model variables.

The mass balance equation for the chamber is

hhd

)(

(2)

where M

is the air mass in the chamber, m

is the

mass flow to the chamber, A

is the cross section

area, ρ

is the air density,

h is the distance from

the chamber water surface to the ambient water

surface and h

is the distance from the ambient water

surface to the top of the chamber.

The pressure force from the chamber is assumed

to equal the buoyancy force. This implies that the

acceleration of the water volume in the chamber is

small.

111111

hApgAh

=⇒=

ΔΔ

(3)

where ρ

is the water density. Insertion of Eq. (2) in

Eq. (3) gives

−=

(4)

The other main equation for describing the

dynamics of the chamber is Newton’s 2’th law used

on the free body with the mass M

c1.

Pressure forces,

gravity and a friction force proportional with the

chamber velocity is assumed to act on the body.

KgMApp

fcacc

1111

)( −−−=

(5)

In order to use an ODE-solver to simulate the one

chamber model, the three states

11 c

px =

and

may be selected resulting in the

differential equation system

⎥

⎦

⎤

⎢

⎣

⎡

−−−

−−

+−−+−

⎥

⎦

⎤

⎢

⎣

⎡

31111

211

)(

))()()

)(((

xKgMApx

ugpxKugK

pxK

fca

avopb

apa

(6)

4 FIVE-CHAMBER DYNAMIC

MODEL

In this section a 5 chamber dynamic model is

described. Although the WD has a complex

geometry the model assumes that each of the five

chambers may be regarded as a control volume with

position independent internal variables and that each

chambers pressure force actuate the WD bode in a

single point. The model consist of 8 differential

equations, 5 equations describing the pressures in

the five chambers derived from mass balance

equations, and 3 equations describing height, trim

and heel derived from Newton’s law.

The five chambers are placed in a “wave dragon”

coordinate system {WD} with the

coordinates

),,(

zyx

. An inertial coordinate

system {I} is placed in the water level as shown on

the figure. The states in the model are the five

chamber pressures (p

, p

), the trim

angle (θ), the heel angle (γ) and the level (h) of the

wave dragon.

A DYNAMIC MODEL OF A BUOYANCY SYSTEM IN A WAVE ENERGY POWER PLANT

Figure 6: Wave dragon coordinate systems.

The mass balance for the n’th chamber is

wan

wcn

−=

is the height in the chamber and not a model state.

Using a rotation matrix

),,(

αγθ

(see (Craig,

1989)), h

and the states are related through

yxh

++−=

)cos()cos(

)sin()cos()sin(

θγ

θγγ

The time derivative of h

is a tedious equation but

using the approximations cos(θ)= 1, cos(γ) = 1,

sin(θ) = θ, sin(γ)= γ assuming small heal and trim

angles (all z

’s are 0) gives the simple relation

++=

θγ

which inserted gives

)(

xgm

wan

wcn

++−=

θλ

(7)

Newton’s 2’th law for the translational system is

)(

ApgM

KpA

wdf

wwwdflh

cnn

−−−+

∑

(8)

where the sum is chamber pressure forces acting on

the wave dragon body. The second term is the forces

from the air chambers containing a constant air mass

(see figure 3). In the model these are approximated

with two chambers. They may be modelled using the

mass balance Eq. (4) but in order to keep the model

order low they are modelled using a static balance.

flh

may be found using the ideal gas law and the

geometrics of the chambers. M

is the total mass of

the wave dragon. The term p

represents the force

from the water reservoir on top the Wave Dragon. It

may be noted that the pressure p

is an input to the

model.

The rotational trim equation is

ypA

cnn

θθ

=−−

∑

(9)

where the sum is the torque from the chambers. The

second term is the torque from the constant air mass

chambers modelled as two symmetrical chambers. It

should be noted that K

flh

as well as K

flθ

are very

dependent on the total air mass in the chambers. The

moment of inertia is calculated as a constant

although it depends on the water level in a very

complex manner. In the simulation a situation with

low water level has been used.

The heel equation is

KKypA

cnn

γγ

γγγ

=−−

∑

(10)

This linear second order equation captures the

gross behaviour of the heel dynamics.

The total model now consist of eleven equations,

equation (7) used 5 times for the five chambers

giving the five states

11 c

px = ,

22 c

33 c

44 c

55 c

px = , equation (8)

with the states

x =

and the equation

gives 2 equations, equation (9) with the

states

and the equation

gives 2 equations, and finally equation (10) with the

states

and the equation

gives 2 equations.

Inserting the states (

1121

,...,, xxx ) gives eleven

nonlinear first order equations. The equations are

solved using an ODE-solver.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

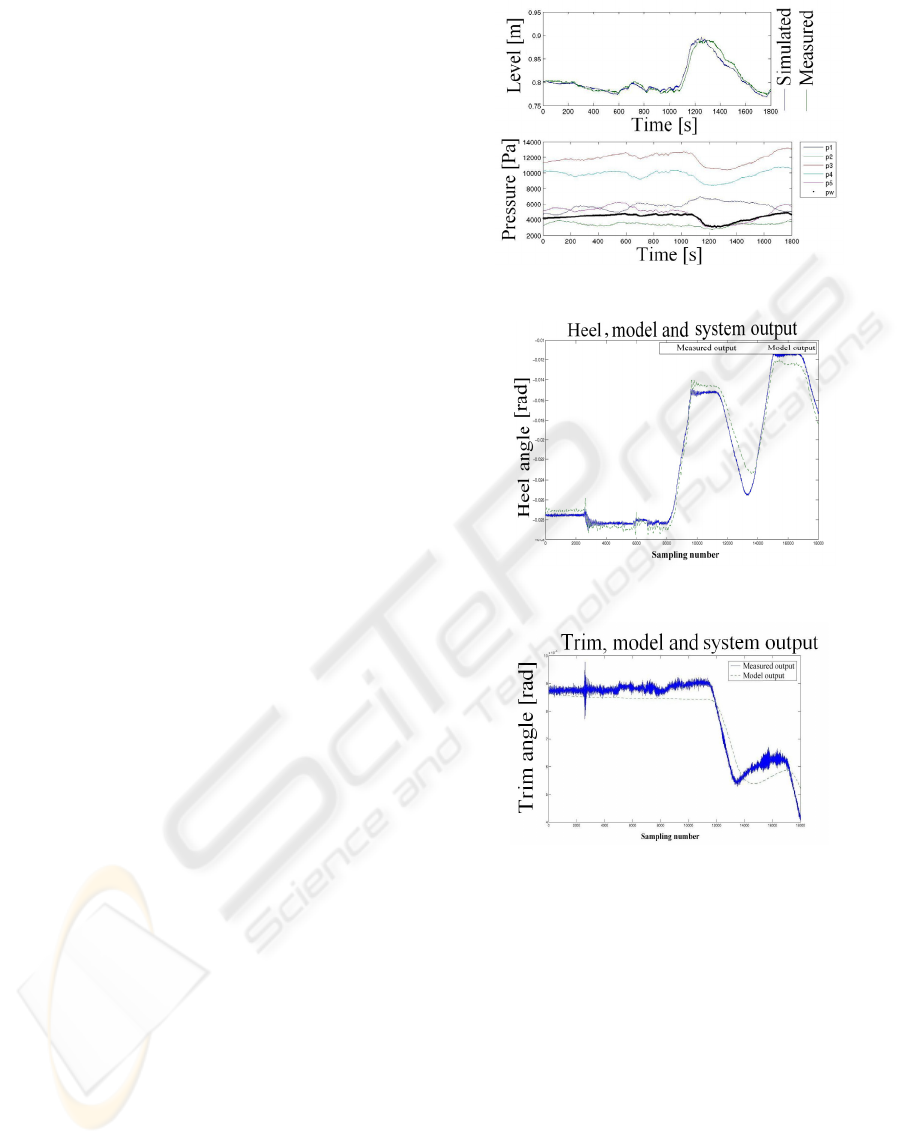
5 SIMULATION

The model is tested using measured data from the

wave dragon. The inputs to the model are the

chamber pressures as well as the water level in the

dragon represented by the pressure measurement p

The reason for not using the valve signals is that

these were not recorded in the data acquisition

equipment. As seen there is a good agreement

between level in the model and the experimental

data. (The agreements are found on the

measurements from the same day. Measurements on

different days are based on different initial pressures

causing identification of slightly different model

parameters) (This is also found on data measured

on the same day.) Because the pressures in the

constant air chambers are not measured these have

been estimated from steady state observations.

The variations on the heel and trim angles are small.

As seen on the figures the behaviour is captures by

the model. All the data were recording prior to this

project and not prepared for this study, unfortunately

the WD run severely aground during the project

meaning that controlled input signal could not be

tested. Regardless of this the model performed well

on the recorded data.

6 CONCLUSIONS

A nonlinear physical model with a complexity that is

suitable for model based control has been presented.

The model is partly based on physical parameters for

the Wave Dragon and may be scaled to a future larger

version. The model has four main equations, one

describing the state of the air in a chamber, and three

accounting for the level, trim and heel motion of the

WD. The model has been validated against measured

WD data, where it captures the gross behaviour of the

Wave Dragon. In particular it describes the response of

the level very well. The model does, however, have one

serious deficiency because it does not capture the

distribution and movement of water in the water

reservoir. A comprehensive study of this is outside the

scope of this paper.

Figure 7: Level simulated and measured.

Figure 8: Heel simulated and measured (Andersen, 2007).

Figure 9: Trim simulated and measured (Andersen, 2007).

REFERENCES

Andersen, J., Hundsdahl, M.Y., Jensen, P.K.,

Vilbergsson, K.S., Vidarsson, O., Skagestad, R., 2007,

Control of Wave Dragon Buoyancy, master thesis,

Aalborg University.

Craig, J.J., 1989, Introduction to Robotics,mechanics and

control, ISBN 0-201-09528-9.

Kofoed, J.P., Frigaard, P. Friis-Madsen, E. Sørensen, H.C.

2006, Prototype testing of the wave energy converter

wave dragon, Renewable Energy 31 181-189.

W.D. Aps , 2006, Wave Dragon – principles,

http://www.wavedragon.net

A DYNAMIC MODEL OF A BUOYANCY SYSTEM IN A WAVE ENERGY POWER PLANT