A GENETIC ALGORITHM APPLIED TO THE POWER SYSTEM

RESTORATION PLANNING PROBLEM

A Metaheuristic Approach for a Large Combinatorial Problem

Adelmo Cechin, José Vicente Canto dos Santos, Arthur Tórgo Gómez and Carlos Mendel

Pipca - UnisinoS, Av. Unisinos 950, São Leopoldo, Rio Grande do Sul, Brazil

Keywords: Genetic Algorithms, Electric Power Systems, Power System Restoration Planning Problem.

Abstract: This work reports the use of a Genetic Algorithm (GA) to solve the Power System Restoration Planning

Problem (PSRP). The solution to the PSRP is described by a series of operations or a plan to be used by the

Power System operator immediately on the occurrence of a blackout in the electrical power supply. Our GA

uses new initialization and crossover operators based on the electrical power network, which are able to

generate and maintain the plans feasible along GA runs. This releases the Power Flow program, which

represents the most computer demanding component, from computing the fitness function of unfeasible

individuals. Results for three different electrical power networks are shown: IEEE 14-Bus, IEEE 30-Bus

and a large realistic system.

1 INTRODUCTION

The Power System Restoration Planning Problem

(PSRP) can be defined as the search for an optimal

sequence of control actions leading a faulty

electrical power system from a restoration state of

operation to a secure state. The secure state is

defined by a normal energy supply with all

operational limits observed. The transition of one

state to the other is performed through a series of

commands sent by the power system operator to the

power system. Each faulty situation demands a

specific sequence of commands to bring, as fast as

possible, the power system back to the secure state.

These operations include the connection and

disconnection of line sections without overloading

the electrical system components.

Further, the PSRP is a multistage problem, being

the objective of each stage the reestablishment of the

service to a group of priority loads. The solution

must obey additional constraints such as those

placed by a priority chain in the energy supply. For

instance, first hospitals must be attended, then public

services, and so on, if distribution context is

considered.

However, the main constraint is the time gap

while consumers are without energy, which must be

kept as small as possible.

The Power System Restoration Planning may be

carried out off or on-line. Off-line plans are typically

based on previous operator experiences in restoring

a faulty system. The efficiency of this process rests

on the ability of the restoration program (or

operator) in finding a similar network state and in

applying the corresponding plan. However, if a new

contingency occurs, a new plan (on-line) has to be

generated. In the simplest case, this can be achieved

by shooting down some part of the network and

bringing it back to a known state, for which a plan

exists. The other solution, certainly better, starts

directly from the actual network state.

Two main classes of algorithms have been used

to solve this problem: deterministic and stochastic

ones. One of the first efforts for treatment of the

PSRP with deterministic techniques was the work of

(Sakaguchi and Matsumoto, 1983), who had created

a Knowledge Based System (KBS) based on the

knowledge of the power system operator. This was

followed by other works using an expert system

approach, such as (Komai et al, 1988) and Kojima et

al (1989). As the size and complexity of electrical

power systems surpassed the capacity of human

control and therefore of rules based on human

knowledge, other methods were developed, such as

(Aoki et al, 1987) using the classical integer

programming approach, (Huang et al, 1991) using

optimization techniques (Nagata et al, 1995) using a

100

Cechin A., Vicente Canto dos Santos J., Tórgo Gómez A. and Mendel C. (2008).

A GENETIC ALGORITHM APPLIED TO THE POWER SYSTEM RESTORATION PLANNING PROBLEM - A Metaheuristic Approach for a Large

Combinatorial Problem.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 100-107

DOI: 10.5220/0001480201000107

 SciTePress

hybrid system of rules and mathematical

programming. For a review on these methods, see

(Curcic et al, 1997). Even for these methods, the

determination of hundreds of discrete variables in

time is a complex task. Therefore, stochastic

methods combined with power flow simulation tools

became an interesting alternative to the deterministic

approaches (Matos et al, 2004).

Stochastic approaches such as Neural Networks

(Hsu and Huang, 1995) (Bretas, 2003) and Genetic

Algorithms (Bretas, 1998) (Luan et al, 2002) are

relatively new and have received some criticisms

such as that they typically use a fixed length string

to represent the solution plan, high computing times

and the low confidence of the power system operator

on the generated plans (Susheela, 2000). In order to

solve these problems, we propose a variable length

solution representation (chromosome) with new

mutation and crossover operators. In relation to the

computing time, first, only feasible solutions are

generated and second, our crossover operator

maintains the feasibility of the plan. This spares time

because the computation of the power flow along the

plan represented in the chromosome does not end in

an unfeasible solution and therefore must not be

immediately discarded. A plan in the population

may have a low score but is rarely discarded because

of unfeasibility. The crossover cut occurs only at

network states in each plan submitted to the

crossover operator.

The third criticism, the confidence of the power

system operator on the obtained solution, can be

partially solved by exhaustively testing and by

carrying out demonstrations on previous cases with

the planner and power flow simulator. However, we

propose in this work that sound solutions may be

obtained if this aspect is considered in the fitness

function already, for instance, by requiring a good

quality solution along the plan and not just at the last

stage of the restoration. Finally, the increase in

computer performance will certainly turn those

methods now just used for the composition of a

restoration plan into on-line solutions with a

response time from seconds to minutes.

This paper is organized as follows: after the

introduction, section 2 presents the restoration

system and its components. Section 3 shows the

Genetic Algorithm component with a description of

the GA operators and section 4 presents results for

three different power systems, the IEEE 14-Bus

system and IEEE 30-Bus (Freris and Sasson, 1968)

and finally the CEEE 146-Bus. Section 5 presents

our conclusions.

2 THE RESTORATION SYSTEM

The main components of the restoration system are

shown in Figure 1. The GA component obtains

information about the network topology by reading

the Electrical Network Topology file. This file

describes the buses with their connected generators

and loads as well the transmission lines among

buses. As an illustration, the upper part of Figure 3

shows a schematic view of the IEEE 14-Bus

topology file. The topology and the actual network

state are used to create an initial population of

feasible solutions. The actual state of the electrical

network is defined by the actual pattern of

connections and activity/inactivity of buses and must

be read from the real network through sensors and

state observers.

Then, during a GA generation, each

chromosome (restoration plan) is used to drive the

whole power system through a series of states, from

the actual state to an end state, hopefully with all

loads restored. Further, the intermediate states of the

network must obey the component limits and

available power for the loads. Each such state is

computed by the Power Flow Program (PFP), whose

results are turn back to the GA. Then, the fitness

function is used to evaluate the restoration plan.

The PFP is called many times for the evaluation

of a chromosome. If the plan in the chromosome is

composed of N stages, then the PFP is called N

times. For example, if a GA needs a population of

size 25 and 25 generations to find a good plan, then

the PFP will be executed 25×25×N times. Our work

spares this time by generating and processing

feasible solutions and leaving a small margin for

unfeasible solutions only in the case of mutated

chromosomes, and only for intermediate solutions

(before the last generation).

The PFP implements the classical fast decoupled

Power Flow method of Stott and (Alsaç, 1974) and

was developed by (Canto dos Santos et al, 2006) In

that work, another approach to the .problem, based

on Linear Programming, was presented.

Figure 1: Restoration system components.

A GENETIC ALGORITHM APPLIED TO THE POWER SYSTEM RESTORATION PLANNING PROBLEM - A

Metaheuristic Approach for a Large Combinatorial Problem

101

3 GENETIC ALGORITHM

COMPONENT

The design of the chromosome format is crucial in

quickly finding an optimal solution. First, the

mutation operator must have a small impact on the

chromosome performance (big random jumps should

be avoided) and second, the crossover operator

should transfer whole functional blocks avoiding

any rough breaking of these functional blocks. In

this work, the time axis is mapped on the linear

chromosome structure.

3.1 Chromosome Representation

Different of the classical GA approach (Goldberg,

1989), the new chromosome representation has a

variable size, consisting of a sequence of stages,

each containing a group of commands sent to the

electrical power system. As the commands are sent,

lines and buses change their state. As will be shown

in the next section, these states are used to define the

crossover points.

For this new proposed representation, each

chromosome codes a sequence of operations or

stages and has a variable size. Not only the whole

sequence has a variable size, but also each stage is

composed of a variable number of operations, which

are executed simultaneously during the restoration

process. Further, the different chromosome sizes and

the requirement for feasibility of the restoration

plans demanded a new crossover operator different

from the classical ones.

Figure 2 shows two different illustrative

representations of the chromosomes. The stages are

shown as discrete elements (white boxes) inside

each chromosome and they contain a group of

operations. Each operation in turn is represented by

a pair of identifiers using the format “<address>:

<operation>”. The operations are divided into two

groups: operations on lines and operations on buses.

The <address> identifies the bus or line on which

the <operation> will be executed. If the operation is

executed on a bus n, its <address> is expressed as

Bn. If it is executed on a transmission line n, its

<address> is Ln. The other identifier represents the

operation. Operations on transmission lines include

the connection of one of its end points (the origin

point or operation O+ and destiny point or operation

D+). Operations on buses may be a load connection

to the bus (operation L+), connection of the power

supply (operation Ger) and the connection of

synchronous compensators to the bus (operation

C+). The system was designed so as to enable

simple additions of other operations as well new

equipment types.

For instance, the second stage in Figure 2

represents the connection of the origins of

transmission line L1 and L2 at the same time.

Figure 2: Chromosome representation as a vector of stages

with discrete operations. The operations are indicated by

mnemonic and numeric codes. The first line shows a

chromosome in a mnemonic format and the second line, in

a numeric format.

3.2 Genome Initialization

The highly flexible representation of the

chromosome demanded the inclusion of specific

program modules for the generation of feasible

chromosome initializations.

In order to obtain feasible initializations, first a

graph is generated in which buses are represented by

nodes and transmission lines by edges. Also, the

buses associated with black start generators (capable

of restarting with no external power source) are at

the root of the graph and are connected with other

buses in a tree-like way. The graph represents the

topology of the power system.

Then, a Random Search (RS) is carried out on

the graph from the root nodes where components

attached to buses are randomly selected. For each

selected component an operation is chosen. Since

many components may be chosen at the same stage,

not only an operation is created, but a whole

operation set may be created and added to the

current chromosome. This way, different operation

sequences are placed in the initial population.

An example of the genome initialization process

is shown in Figure 3 for the IEEE 14-Bus power

system topology composed of 14 buses, 18

transmission lines, 2 generators and 11 loads

(arrows). In this example, the objective is to find a

sequence of operation sets, which should lead the

power system from an initial state characterized by

total blackout to a final state with all loads supplied.

The nodes in the topology graph represent the buses

and the links the transmission lines. In the real

operation, these data are obtained from a supervisory

system. In the first step (topology graph (1)), only

the bus 1 (node 1) is activated, fed by the generator

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

102

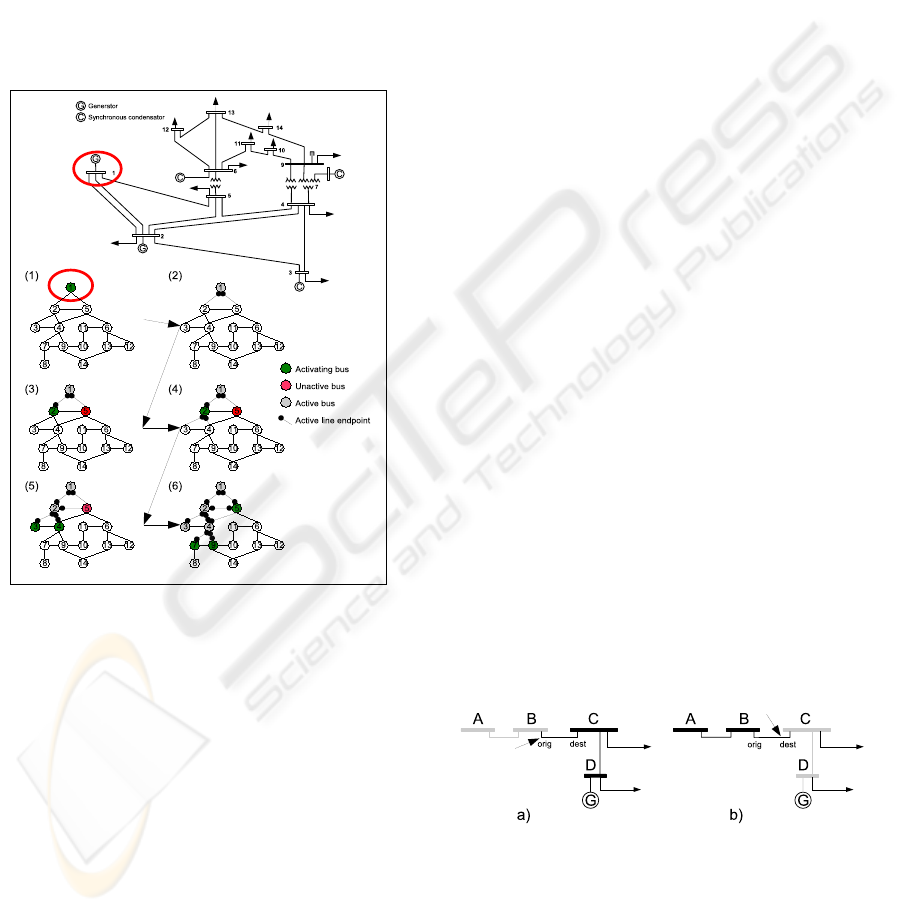
(black start capable generator) connected to the bus.

Then (graph (2)), the algorithm computes which are

the nodes linked to already activated nodes such as

in a Random Search. From the nodes allowed to be

activated, the algorithm chooses randomly if they

shall be activated or not generating different

individuals. In the next steps, the algorithm proceeds

considering all the nodes directly linked to the

already activated nodes and determines if and which

ones shall be activated. Note that the algorithm may

activate more than one bus at the same time. For

instance, from graph (4) to graph (5), both buses 3

and 4 (nodes 3 and 4) were activated simultaneously.

Figure 3: Demonstration of the genome initialization

process for the IEEE 14-Bus system. The graph is

searched and the corresponding buses are randomly

activated. At each step, inactive buses have a renewed

opportunity to be activated by the algorithm. Buses are

indicated by numbers, transmission lines by solid lines and

loads by arrows.

The resulting activations during these steps are

accordingly indexed in the genome in the form of

operations, and the initialization process continues

until all the nodes are connected to active buses and

the number of inactive nodes reaches a previously

chosen random limit. Therefore, different solutions

are generated, all of them considering possible

pathways described in the topology graph. For

instance, there is no sense in connecting bus 14

before bus 9 or bus 13 is activated. The randomness

of the bus activation creates chromosomes with

diverse solution strategies ensuring a good coverage

of the solution space.

3.3 Crossover Operator

Due to the more flexible representation of the

chromosome, a new crossover operator was

developed, which avoids improper operations, such

as the connection of a load or generator (not the

black start capable generator) to a bus without

power.

The classical GA crossover cuts two

chromosomes at the same position because there is

an exact correspondence between both left and right

sides of the chromosomes. However, the flexibility

of the operation positioning inside the variable size

chromosome demands the computation of

synchronization states in the parents’ chromosomes.

Each stage in a chromosome is associated with a

network state, which is used by the crossover

operator. This state is the result of all operations of

all stages to the left side (before) of the respective

chromosome stage and of the operations in the stage.

Lines may be in one of four states:

• not connected;

• origin point connected;

• end point connected;

• totally connected.

Each end of a transmission line was modeled by a

different connection for two reasons: first, this is

more realistic, resulting in solutions that can be

readily understood by the system operator and

second, if the line model had included just one

connection, then the activation of the line would

automatically activate both connected buses at the

same time.

Figure 4 shows an example how a line is

activated, depending on the sequence of bus

activation and end connections.

Figure 4: Example of how a line may be activated from

different sides. In case a) the line is activated by the bus B

if it is activated and the “orig” end of the line is connected.

In the case b), the line is activated if the bus C is activated

and the “dest” end is connected.

A GENETIC ALGORITHM APPLIED TO THE POWER SYSTEM RESTORATION PLANNING PROBLEM - A

Metaheuristic Approach for a Large Combinatorial Problem

103

For the buses, the allowed states are:

• inactive bus (disconnected);

• bus activated - when the bus has power from a

transmission line or generator;

• generator connected;

• load connected;

• synchronous compensator connected.

The states of the buses in both chromosomes are

compared, and if the network state is the same, they

are equivalent.

All the equivalent state pairs are stored in a list,

and a position in the list is randomly chosen, which

represents the stage at which the two sequences will

be cut and where the crossover occurs.

A consequence of the use of this operator is that

the resulting sequences (children) have a different

number of operations reaching the same state, which

means that some of them will be smaller and,

possibly, more efficient than the others.

This process is illustrated in Figure 5. In this

case, a new chromosome generated by crossover of

the left side of the upper chromosome and the right

side of the lower chromosome may be better than

both parent chromosomes in terms of number of

stages. The left side of the upper chromosome takes

a smaller number of stages to reach the same state

than the lower chromosome and it will be

transmitted to the children chromosome.

Figure 5: Determination of equivalent stages in two

chromosomes of the genome. Different pairs of equivalent

stages are stored in a list and one of them (the white one,

for instance) is randomly chosen. Dotted lines show the

stages in the chromosomes where the two sequences are

divided for the crossover operation.

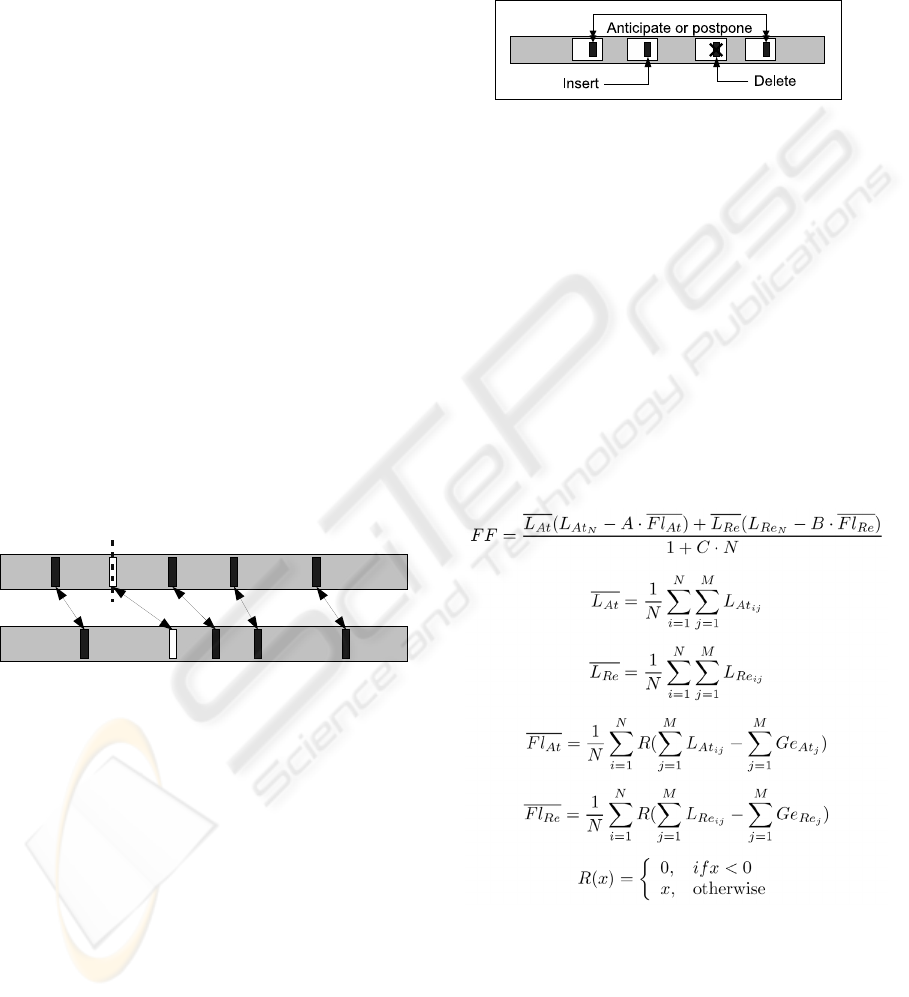
3.4 Mutation Operator

There are three types of mutations: inclusion and

exclusion of an operation in one stage and

permutation of operations in two stages. As an

illustration of the steps performed by the mutation

operator, see Figure 6. Because these are

unrestricted operations on the chromosome, these

may generate unfeasible solutions with respect to the

delivered and consumed power. Unfeasible solutions

are tolerated only at intermediate generations of the

GA and intermediate stages of the chromosome

because this increases the diversity of solutions and

helps the GA to escape local minima. For instance, a

certain load requiring more power than available

may be connected during intermediate generations.

However, only feasible plans are considered in the

end generation.

Figure 6: Representation of possible mutations. The white

rectangles represent stages and the black ones, possible

operations in the stages. The operations can be included,

excluded or transferred from one stage to another by the

mutation operator.

3.5 Fitness Function

In order to compute the fitness function, the

operations described in the chromosome are used by

the PFP to compute the power flow at each stage.

In this work, the flexibility of the fitness function

was maintained by the use of parameters (A, B and C

in the following equations) allowing a detailed

analysis of the influence of each system variable on

the solution obtained by the GA. The fitness

function FF is defined by:

where M is the number of buses in the power

system, N is the number of stages, L

and L

are the

active and reactive loads respectively, Ge

and Ge

are the generated active and reactive power

respectively, and A, B and C are trimming constants.

i and j denote the stage and bus respectively and

R(x) is the ramp function.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

104

The main component of the fitness function is the

supplied active and reactive loads at the last stage N,

and L

. However, tests with just these

variables presented solutions which were not

balanced along the stages and are difficult to be

accepted by the system operator. The inclusion of

the mean of the loads along the stages intends to

meet, at each stage, the highest possible number of

active and reactive loads, a good distribution of

supplied loads along the stages and a sound solution

to the system operator.

Parameters A and B decrease the fitness function

of individuals in case the generated power is lower

than the total load of the system and therefore help

to discard any unfeasible solution generated during

the GA runs by the mutation operator. The inclusion

of the supply power failure in the fitness function

intends to obtain solutions whose power generation

is sufficient to attend all the connected loads. The

parameters A and B control how tolerant is the GA

to unfeasible solutions during runs. This allows

suboptimal solutions to remain in the population and

thus contributing to maintain the diversity of the

population. Both parameters may be increased in the

last few generations leaving only feasible solutions

in the population.

Since the quick evaluation of the PFP is the main

concern for a practical use of the GA, the PFP needs

only to compute the state of the connected part of

the network. Then, as the restoration program goes

through each stage in the chromosome, only the

buses and lines necessary to the execution of the

current stage are transferred to the PFP, reducing the

number of nodes and edges the PFP has to consider

during the calculations. As the electrical network

gets more and more connected with each new stage,

its size increases and the computations in the PFP

become harder to carry out.

Other fitness functions were designed. However,

the previous fitness function resulted in the best

solution plans, with a quick attendance of the needed

power while maintaining the power generation

restrictions.

4 RESULTS

In this section, results of experiments performed

with three different power systems, the IEEE 14-Bus

system, IEEE 30-Bus and finally the CEEE 146-Bus,

three power systems with increasing degree of

complexity are shown. Each experiment used a

different population initialization and all electrical

parameters of the systems were monitored, such as

the active and reactive powers of the best genome in

each generation. After running each experiment, the

best genome in the population is shown in a graphic

representation. As each stage corresponds to a group

of operations executed on the power system and the

execution of each such operation spends time, a

correspondence can be made between the

consecutive execution of those stages and the

restoration elapsed time. It will be assumed that each

stage takes one unit of time to be executed.

It was considered the occurrence of a general

blackout in the IEEE 14-Bus (Freris and Sasson,

1968) system and that only the generator at bus 1 is

black start able. Also, all the 20 branches are

available for the restoration.

In Figure 7, the evolution of the GA with three

different initializations is presented. Typically, the

GA starts with 40-50 stages (dashed lines) and a

fitness function of 0.75 (solid lines) of the maximum

value, showing that many solutions generated by our

method have a high fitness function (and feasible) at

the GA initialization already. As the GA computes

new solutions, the fitness function increases and the

number of stages needed to reach it decreases.

Figure 7: Three GA runs for the IEEE 14-Bus System,

with a population size=25 chromosomes and fitness

function FF with parameters A=1, B=5 and C=1. Solid

lines represent the value of the normalized fitness function

for the three runs (scale at the left side of the graph) while

dashed lines represent the number of stages (scale at the

right side of the graph) of the best solution in the

population.

Figure 8 shows the corresponding plan obtained.

The generated and delivered power of the best

individual in the population is shown along the

restoration stages. Results for the power system

IEEE 30-Bus using the same GA parameters are

shown in Figure 9. It can be observed that the GA

obtained an efficient solution in terms of used

power. For instance, once the difference between

generated and consumed reactive power reaches

zero, there is an increase in the power generated so

as to supply the new loads. Afterwards, the loads are

connected to the system until that margin reaches

A GENETIC ALGORITHM APPLIED TO THE POWER SYSTEM RESTORATION PLANNING PROBLEM - A

Metaheuristic Approach for a Large Combinatorial Problem

105

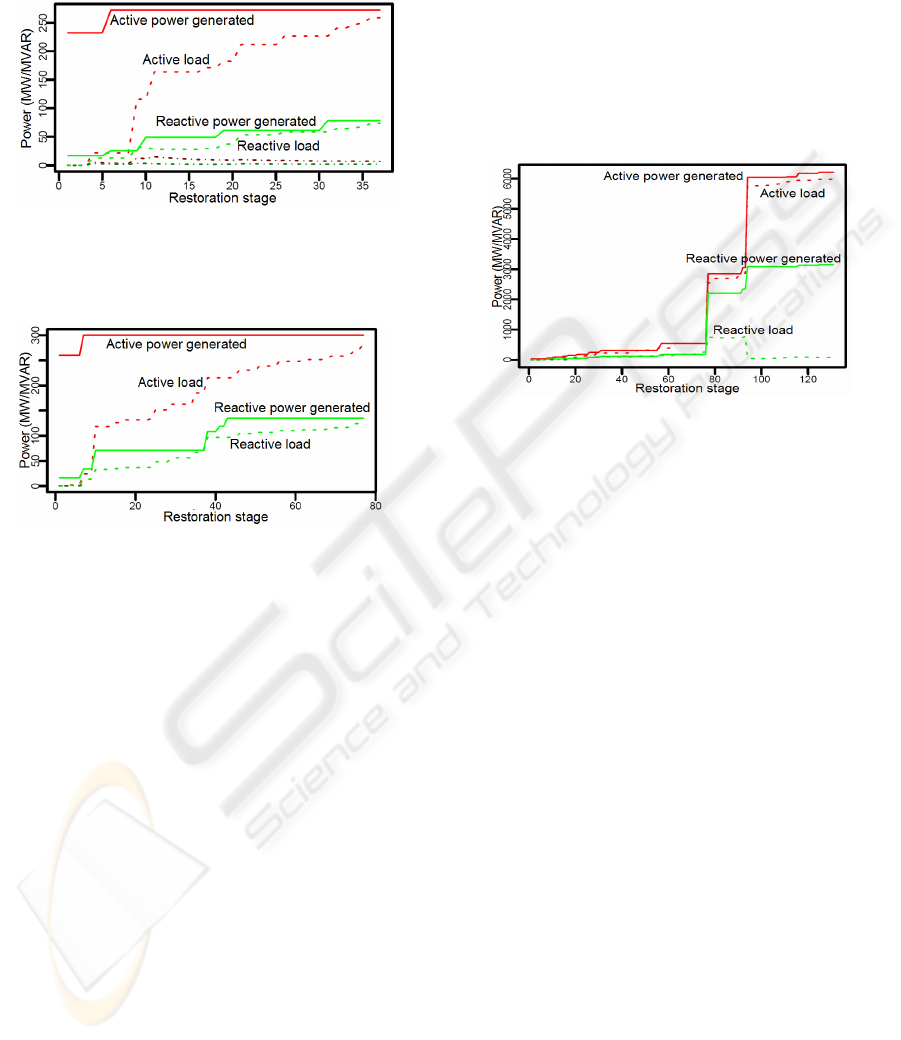
zero again, and so on. Further, as expected, the plan

for a larger power system such as the IEEE 30-Bus

demands more stages, for instance, 37 for the IEEE

14-Bus and 78 for the IEEE 30-Bus .

Figure 8: Restoration of the IEEE 14-Bus. Solid lines

represent the active and reactive power generated while

the dashed ones represent the power consumed or the total

loads.

Figure 9: Restoration of the IEEE 30-Bus power system.

Solid lines represent the active and reactive power

generated while the dashed ones represent total loads.

Finally, we tested the GA algorithm with the CEEE

(a real life Brazilian system) power system

composed of 146 buses and 196 transmission lines

in south Brazil. Figure 10 shows one of the obtained

plans. Approximately 130 stages are needed to

restore the full system from a complete blackout.

Certainly, the set of experiments presented in

this section represents only part of all test performed

with our approach. Other tests varying the number of

generations, population size, fitness function and

parameters were performed too.

5 CONCLUSIONS

The objective of this work was to show a restoration

system based on a GA that presents efficient plans to

the power system operator when a blackout or any

other serious lacks occurs. The use of GA for the

generation of operation sequences, or strategies is

only possible with the careful codification of the

operation sequences in the chromosome taking into

account the electrical power network topology. If the

task of determining the feasibility of the solutions is

entirely left to the PFP, then the GA generates many

unfeasible solutions with a direct impact on the

performance of the GA. Also, there must be a limit

on the number of allowed generations if the system

is to be used in an on-line modus. For example, in

this work, this number was set to 25 generations. All

this enable the GA to quickly find a solution without

wasting of time computing the power flow for

unfeasible individuals.

Figure 10: Power system restoration plan for the CEEE

System, obtained with a GA with a population size=25,

number of generations=25, and parameters A=1, B=5 e

C=1.

The choice of the fitness function is important to

define the quality of the obtained solution. In this

work, a parameterized function was chosen as a

good compromise among user priorities, flexibility

and complexity of the function. Also, a good

distribution of connection operations along the plan

represents a sound solution for the operator. In this

respect, we observe that there are no works

considering the quality of operation stages along the

plan in terms of soundness for the system operator,

as proposed in this article. Certainly, this is one of

the causes for the low confidence level of system

operators on solutions obtained by stochastic

algorithms.

However, some care must be kept in relation to a

solution found by stochastic algorithms. A GA may

find a good solution in terms of fitness function but

it may be unfeasible. The stochastic freedom of GA

solutions may be kept at the intermediate

generations with the risk of reaching the last

generation with unfeasible plans in the whole

population. For example, if the best individual is

good but unfeasible, its genes may propagate along

the population making all of them unfeasible. This is

called lost of diversity in the GA area. Therefore,

there must be a compromise between keeping all the

time all the solutions feasible (for example, making

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

106

the parameters A and B very high) and maybe

loosing a good solution, and leaving the GA

completely free to generate and process any solution

plan. We think that in this respect we could attain a

good compromise by allowing only the mutation

operator to generate unfeasible solutions at

intermediate generations and also by considering

only feasible end solutions in the last generation.

Finally, researches in progress point out to the

need of inclusion of more complex and realistic

simulations, such as the dynamical behavior of the

electrical power system. For example, the simulation

of voltage and current overshooting during

switching operations, which can cause the breaking

of lines by limiting current and voltage devices,

could preview an instable system reaction leading

the power system to a complete blackout. Since this

analysis increases the processing time of the PFP,

any such addition makes the feasibility analysis

presented in this work even more important.

Currently, the use of other metaheuristics,

specifically Tabu Search, is being studied and will

be published in the future.

REFERENCES

Aoki, K., Kuwabara, H., Satoh, T., Kanezashi, M. (1987)

Outage state optimal load allocation by automatic

sectionalizing switches operation in distribution

systems. IEEE Trans. Power Delivery PWRD-2:

pp.1177-1185.

Bretas, N., Delben, A. and Carvalho, A. (1998) Optimal

energy restoration for general distribution systems by

genetic algorithm. In Power System Technology, 1998

International Conference on, volume 1, pages 43–47.

Bretas, A. and Phadke, G. (2003) Artificial neural

networks in Power System Restoration. IEEE

Transactions on Power Delivery, 18(4):1181–1186 .

Canto dos Santos, J., Gómez, A., Rodrigues, A. (2006) An

optimization algorithm to improve security of

electrical energy systems. In ICINCO 2006 - 3rd Int.

Conf. on Informatics in Control, Automation &

Robotics. Setubal - Portugal. INSTICC Press.

Curcic, S., Ozveren, C.S., Lo, K.L. (1997) Computer-

based strategy for the restoration problem in electric

power distribution systems. Inst. Electr. Eng. Proc.

144: 389-398.

Freris, L., Sasson, A. (1968) Investigation of the Load

Flow Problem, Proceedings of IEE, 115(10): 1459-

1470.

Goldberg, David E. (1989) Genetic Algorithms in search,

optimization, and machine learning. Addison Wesley

Longman Inc.

Hsu, Y. and Huang, H. (1995) Distribution systems

service restoration using the artificial neural network

approach and pattern recognition method. In IEE

Proceeding on Generation, Transmission and

Distribution, volume 142, pages 251–256.

Huang, J.. Galiana, F. and Vuong, G. (1991) Power

system restoration incorporating interactive graphics

and optimization. In Power Industry Computer

Application Conference, 1991. Conference

Proceedings, pages 216–222, Baltimore.

Komai, K., Matsumoto, K. and Sakaguchi, T. (1988)

Analysis and evaluation of expert’s knowledge for

Power System Restoration by mathematical

programming method. IEEE International Symposium

on Circuits and Systems, 2(1):1895–1898.

Kojima, Y., Warashina, Nakamura, S. and K. Matsumoto,

K. (1989) The development of power system

restoration method for a bulk power system by

applying knowledge engineering techniques. IEEE

Transactions on Power Systems, 4(2):1228–1235.

Luan, W., Irving, M. and Daniel, J. (2002) Genetic

algorithm for supply restoration and optimal load

shedding in power system distribution networks. In

IEE Proceeding on Generation, Transmission and

Distribution, volume 149, pages 145–151.

Matos, M., Ponce de Leão, M., Saraiva, T., Fidalgo, J.,

Miranda, V., Lopes, J., Ferreira, R., Pereira, J., Proença,

M., Pinto, J., (2004). Metaheuristics applied to power

systems in Metaheuristics: computer decision-making,

Kluwer Academic Publishers, Norwell, MA, USA

Nagata, T., Sasaki, H. and Yokoyama, R. (1995) Power

System Restoration by joint usage of expert system

and mathematical programming approach. IEEE

Transactions on Power Systems, 10(3):1473–1479.

Sakaguchi, T. and Matsumoto, K. (1983) Development of

a knowledge based system for Power System

Restoration. IEEE Transactions on Power Apparatus

and Systems, PAS-102(2):320–329.

Stott, B., Alsac, O. (1974) Fast Decoupled Load Flow.

IEEE Transactions Power Apparatus and Systems,

Vol 93, May / June 1974, pp. 859-869.

Susheela, D.V. and Murty M.N. (2000) Stochastic search

techniques for post-fault restoration of electrical

distribution systems. Sadhana, vol. 25, Part 1,

February 2000, pp. 45-56.

Wu, F. and Monticelli, (1988) A. Analytical tools for

Power System Restoration - conceptual design. IEEE

Transactions on Power Systems, 3(1):10–16.

A GENETIC ALGORITHM APPLIED TO THE POWER SYSTEM RESTORATION PLANNING PROBLEM - A

Metaheuristic Approach for a Large Combinatorial Problem

107