SHOE GRINDING CELL USING VIRTUAL MECHANISM

APPROACH

Bojan Nemec and Leon Zlajpah

Jozef Stefan Institute, Jamova 39, 1000 Ljubljana, Slovenia

Keywords:

Robotics, Redundant robot control, Force control, Shoe grinding.

Abstract:

The paper describes the automation of the shoe grinding process using an industrial robot. One of the major

problems of ﬂexible automation using industrial robots is how to avoid joint limitations, singular conﬁguration

and obstacles. This problem can be solved using kinematically redundant robots. Due to the circular shape of

the grinding disc, the robot becomes kinematically redundant. This task redundancy was efﬁciently handled

using virtual mechanism approach, where the tool is described as a serial mechanism.

1 INTRODUCTION

Shoe production is most likely labor intensive; the

rate of automation is usually low. Therefore it is con-

sidered as the industry suitable for the counties with

low labor cost (Taylor and Taylor, 1988; Nemec and

et all, 2003). In last years new aspect in shoe pro-

duction is arising - custom made shoes (Dulio and

Boer, 2004). The customization in mass shoe pro-

duction requires complex information system and full

automation of planning, production and distribution

processes. One of the major challenges is how to gen-

erate robot trajectories base solely on the CAD model

of the shoe. Manual teaching and trajectory test-

ing phases are not acceptable for customized shoes,

where virtually each work-piece on the production

line can differ from the previous one. Therefore, we

haveto design tools which enable to generate fault tol-

erant robot trajectories. This is usually accomplished

using complex task planning algorithms, which are in

most cases off-line batch procedures. In (Nemec and

Zlajpah, 2008) we proposed a solution based on con-

trol algorithms for the kinematicaly redundant robot,

where we sacriﬁced exact orientation of the tool in

order to achieve additional degrees of redundancy. In

this paper, we propose a new approach, called virtual

mechanism approach. The proposed algorithm was

applied to the shoe grinding cell, which uses an in-

dustrial robot with 7 D.O.F.

2 SOLVING TASK KINEMATIC

REDUNDANCY USING

VIRTUAL MECHANISM

APPROACH

Robotic systems under study are n degrees of free-

dom (DOF) serial manipulators. We consider redun-

dant systems, which have more DOF than needed to

accomplish the task, i.e. the dimension of the joint

space n exceeds the dimension of the task space m,

n > m and r = n − m denote the degree of the re-

dundancy. Let the conﬁguration of the manipulator

be represented by the a vector q

of n joint positions,

and the end-effector position (and orientation) by m-

dimensional vector x

of the robot tool center point

positions (and orientations). The relation between the

joints and the task velocities is given by the following

well known expression

= J

(1)

where J

is the m×n manipulator Jacobian matrix.

The solution of the above equation for

can be given

as a sum of the particular and the homogeneous solu-

tion

+ N

ξ (2)

where

= W

−1

)

−1

. (3)

Here,

is the weighted generalized-inverse of J

, W

is the weighting matrix, N

= (I−

) is a n×n ma-

trix representing the projection into the null space of

, and ξ is an arbitrary n dimensional vector. We will

denote this solution as the generalized inverse based

159

Nemec B. and Zlajpah L. (2008).

SHOE GRINDING CELL USING VIRTUAL MECHANISM APPROACH.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 159-164

DOI: 10.5220/0001480901590164

 SciTePress

redundancy resolution at the velocity level (Nenchev,

1989). The homogenous part of the solution belongs

to the Jacobian null-space. Therefore, we will denote

it as

= N

ξ . Now consider the case where

the robot Jacobian matrix J

is deﬁned in Cartesian

(world) coordinate system and the dimension of the

Jacobian is 6×n, but the task is described in another

coordinate system. It can be shown that the transfor-

mation from the Cartesian to the task space can be

very complex. As an alternative approach we propose

to model the tool as a serial kinematic link. Let con-

sider the general case where the robot holds the object

to be machined and the work tool is ﬁxed, as illus-

trated in Fig. 1. In such a case, we can deﬁne the

direct kinematic transformation as

Figure 1: The robot holds the object and the work toll is

ﬁxed.



R I



= x

+ x

(4)

where x

is the robot Cartesian position and orienta-

tions, R is the robot tool rotation 3× 3 dimensional

matrix, x

is the 6 × 1 vector of the object position

and orientation, x

is the 6 × 1 vector of position and

orientation of the top of the virtual mechanism and

6× 1 vector x

describes the distance and orientation

between the base coordinates system and the work

tool coordinate system. Let consider robot and virtual

mechanism as one mechanism with n+ n

degrees of

freedom. The conﬁguration of the virtual mechanism

can be described with the n

× 1 dimensional vector

. The new task position is

x = x

− x

(5)

and the Jacobian of this new mechanism can be ex-

pressed as

J = [J

| − J

] (6)

where the Jacobian of the virtual mechanism J

is de-

ﬁned as

∂x

∂q

. (7)

As we can see, the task space preserves it’s dimen-

sion, while the joint space is increased with the di-

mension of the virtual mechanism. This approach has

two major advantages. First, we can use the existing

robot Jacobian, which is assumed to be known. Sec-

ond, the augmented part of the Jacobian has very sim-

ple structure in most cases. Note that Eq. 4 does not

handle orientations correctly, since orientation vec-

tors can not be simply added in general case. There-

fore, using Eq. 4 and 5 we obtain an approximate so-

lution regarding the orientation vector. In most cases,

the difference between the desired and the real orien-

tation vector is small and is acceptable for operations

like brushing and polishing. If orientations are impor-

tant, we can use equation 4 and 5 for the calculation

of positions only, while the orientations have to be

calculated using rotation matrices as follows.

= R

R (8)

Here, R

and R

are 3×3 rotation matrices describing

object rotation against virtual mechanism and virtual

mechanism rotation expressed in the robot base co-

ordinate system. The corresponding orientation vec-

tor can be than obtained using the transformation of

the rotation matrix to the orientation vector described

with euler or roll pitch yaw notation. Note that using

this ’correct’ transformation also rotation part of the

Jacobian described by Eq. 6 becomes more complex.

On the other hand, when the Jacobian is used in the

control loop, only approximate values of Jacobian are

needed. Therefore, control algorithm based on Jaco-

bian deﬁned by Eq. 6 gives equal results as control

algorithm using the Jacobian calculated from rotation

matrices, as described with Eq. 8.

3 CONTROL

Using the virtual mechanism approach, we can di-

rectly apply any control algorithm for the kinemati-

cally redundant robot. A suitable choice is the con-

trol law using generalized inverse-based redundancy

resolution at velocity level in the extended opera-

tional space. Redundancy resolution at the velocity

level is favorable because it enables direct implemen-

tation of the gradient optimization scheme for the sec-

ondary task. The gradient projection technique has

been widely used for the calculation of the null space

velocity that optimizes the given criteria. The rea-

son for this is that a variety of performance criteria

can be easily expressed as gradient function of joint

coordinates. Although the control law using general-

ized inverse-based redundancy resolution at velocity

level can not completely decouple the task and the

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

160

null space (Oh et al., 1998; Park et al., 2002; Ne-

mec and Zlajpah, 2000; Nemec and Zlajpah, 2001),

it enables good performance in real implementation

(Nemec et al., 2007). The joint space control law is

= HJ

(

+ K

−

q) +

HN(

+ K

−

q) + h

h+ J

f (9)

where J is the Jacobian matrix, H is n× n inertia ma-

trix, h

h is n-dimensional vector of the centrifugal, cori-

olis and gravity forces, f

f is n-dimensional vector of

the external forces acting on the manipulator’s end ef-

fector and K

, K

and K

are diagonal matrices

representing positional, velocity, force and null-space

feedback gains. The ﬁrst term of the control law cor-

responds to the task-space control torque τ

, the sec-

ond to the null-space control torque τ

and the third

and the fourth is used to compensate the non-linear

system dynamics and the external force, respectively.

Here, e

= x

− x

x are the task-space tracking error,

= f

− f

f and

−

is the null-space track-

ing error. x

, f

and

are the desired task coordi-

nates, desired force and the desired null space veloc-

ity, respectively. The details of the control law deriva-

tion can be found in (Nemec and Zlajpah, 2000; Ne-

mec et al., 2007).

An attention should be paid on the selection of the

inertia of the virtual link. The inertia matrix H has the

form

H =



0 H



(10)

where H

is the robot inertia matrix and H

is the di-

agonal matrix describing the virtual mechanism iner-

tia. Clearly, H

can not be zero, but arbitrary small

values can be chosen describing the lightweight vir-

tual mechanism. Selection of the inertia matrix of the

virtual mechanism affects only the null space behav-

ior of the whole system. Heavy virtual links with high

inertia would slow down the movements of the virtual

links. Therefore, low inertia of virtual links is an ap-

propriate choice. On the contrary, we can assume that

no gravity, coriolis and centrifugal forces act on the

virtual links and the corresponding terms in the vector

h can be set to zero. Control law 9 assumes feedback

from all joints, including non-existing virtual joints.

There are multiple choices how to provide the joint

coordinates and the joint velocities of the virtual link.

A suitable method is to build a simple model com-

posed of a double integrator

−1

(11)

where τ

is the part of the control signals correspond-

ing to the virtual link.

4 MOTION OPTIMIZATION

As we mentioned previously, one of the main prob-

lems in automatic trajectory generation is the inabil-

ity to assure that the generated trajectory is feasible

using a particular robot, either because of possible

collisions with the environment or because of the lim-

ited workspace of the particular robot. Limitations in

the workspace are usually not subjected to the tool

position, but rather to the tool orientation. Another

sever problem are wrist singularities, which can not

be predicted in the trajectory design phase on a CAD

system. A widely used solution in such cases is off-

line programming with graphical simulation, where

such situation can be detected in the design phase

of the trajectory. Unfortunately this is a tedious and

time consuming process and therefore not applicable

in customized production, where almost each work

piece can vary from the previous one (Dulio and Boer,

2004; Nemec and Zlajpah, 2008). The problem can be

efﬁciently solved using the null space motion, which

changes the robot conﬁguration, but does not affect

the task space motion. The force and the position

tracking are of the highest priority for a force con-

trolled robot and are therefore considered as the pri-

mary task. The secondary task is deﬁned by the opti-

mization of a given cost function.

Let p be the desired cost function, which has to be

maximized or minimized. Then the velocities

= kNH

−1

(

δp

δq

δp

δq

, .....

δp

δq

, ) (12)

in Eq 12 maximize cost function for any k > 0 and

minimize cost function for any k < 0 (Asada and Slo-

tine, 1986), where k is an arbitrary scalar which de-

ﬁnes the optimization step. In our case we have se-

lected a compound p which maximizes the distances

between obstacle and the robot links or robot work

object, maximizes the distance to the singular con-

ﬁguration of the robot and maximizes the distance in

joint coordinates between current joint angle and joint

angle limit. We deﬁne the cost function as a sum

of three cost functions p = p

+ p

, where p

denotes cost function for obstacle avoidance, p

cost

function for avoiding joint limits and p

cost function

for singularity avoidance. We select the cost func-

tion for obstacle avoidance as (Khatib, 1986; Khatib,

1987) p

, where E is an l × l rotation matrix

describing the direction of an artiﬁcial potential ﬁeld

pointing from the obstacle, l is the dimension of the

position sub-space and d

is the shortest distance be-

tween the obstacle and the robot body. In our case the

desired objective is fulﬁlled if the imaginary force is

applied only on the robot joints. The cost function for

the joint limits avoidance is deﬁned as (Nemec and

SHOE GRINDING CELL USING VIRTUAL MECHANISM APPROACH

161

Zlajpah, 2008; Chaumette and Marchand, 2001)







max

− q)

, |q

max

− q)

| < ε

min

− q)

, |q

min

− q)

| < ε







(13)

where ε is a positive constant deﬁning the neighbor-

hood of joint limits. For the singularity avoidance

we use the manipulability index deﬁned as(Asada and

Slotine, 1986)

|JJ

| (14)

Then, the desired null space velocity for our task are

calculated using

= NH

−1

Vd − 2k

− q

q) − 2k

δJ

δq

(15)

Matrix J

is the Jacobian matrix calculated from the

robot base to the robot wrist. Scalars k

, k

and k

are

appropriate positive constants deﬁning the optimiza-

tion step. In real implementation, k

and k

are set to

zero if the observed point is away enough from the

possible collision points and joints are far away from

their limits, respectively. Similar, the last term of

is not computed if the manipulability index is large

enough. Unfortunately, the partial derivative

δJ

δq

is not

easy to calculate. However, we can use the numerical

derivative of the manipulability measure p

instead.

Vector q

denotes the physical joint limit in the range

min

, q

max

5 SHOE GRINDING

In the shoe assembly process, in order to attach the

upper with the corresponding sole, it is necessary to

remove a thin layer of the material off the upper sur-

face so that the glue can penetrate the leather. To

do this, the robot has to press the shoe against the

grinding disc with the desired force while executing

the desired trajectory. In the past, there were sev-

eral approaches how to automate this operation. For

mass production, there are special NC machines avail-

able. Their main drawback is relatively complicated

setup and are therefore not suitable for the custom

made shoes. Required ﬂexibility is offered by the

robot based grinding cell. In the EUROShoeE project

(Dulio and Boer, 2004), a special force controlled

grinding head has been designed. The robot manipu-

lated with the grinding head while the shoe remained

ﬁxed on the conveyor belt (Jatta et al., 2004). The

main drawback of this approach is relatively heavy

and expensive grinding head. Additionally,force con-

trol can be applied only in one direction. In our ap-

proach, the robot holds the shoe and presses it against

the grinding disc of a standard grinding machine as

used in the shoe production industry. The impedance

force control was accomplished by the robot using

universal force-torque sensor mounted between the

robot wrist and the gripper which holds the shoe last.

It is well known that the kinematic redundancy en-

ables greater ﬂexibility in execution of complex tra-

jectories. For example, also humanoid hand dex-

terity is subjected by it’s is kinematical redundancy.

We used Mitsubishi Pa10 robot with 7 D.O.F in our

roughing cell, which has one degree of redundancy.

Additional two degrees of redundancy were obtained

by treating the grinding disc as a virtual mechanism.

The surface of the grinding disc can be naturally de-

scribed with the outer surface of the torus, where R

and r are the corresponding radius of the grinding

disc, as shown in the Fig. 2. Let x be the task (Carte-

sian) coordinate of the whole system. Assuming that

the robot tool position and robot Jacobian is known,

the forward kinematics can be easily expressed as

Figure 2: Rotary brush presented as torus.

x = x







(R+ rc

)

(R+ rc

)

−ϕ







, (16)

while the corresponding Jacobian is

J =







(R+ rc

) −s

0 rc

−s

(R+ rc

) − c

0 0

−1

0 1







. (17)

Here, we used the abbreviation c

= cos(ϕ), c

cos(γ), s

= sin(ϕ) and s

= sin(γ). Thus we have 9

degrees of freedom, 6 of them are required to describe

the grinding task, while the remaining three degrees

of freedom are used for the obstacle avoidance, joint

limits avoidance and singularity avoidance.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

162

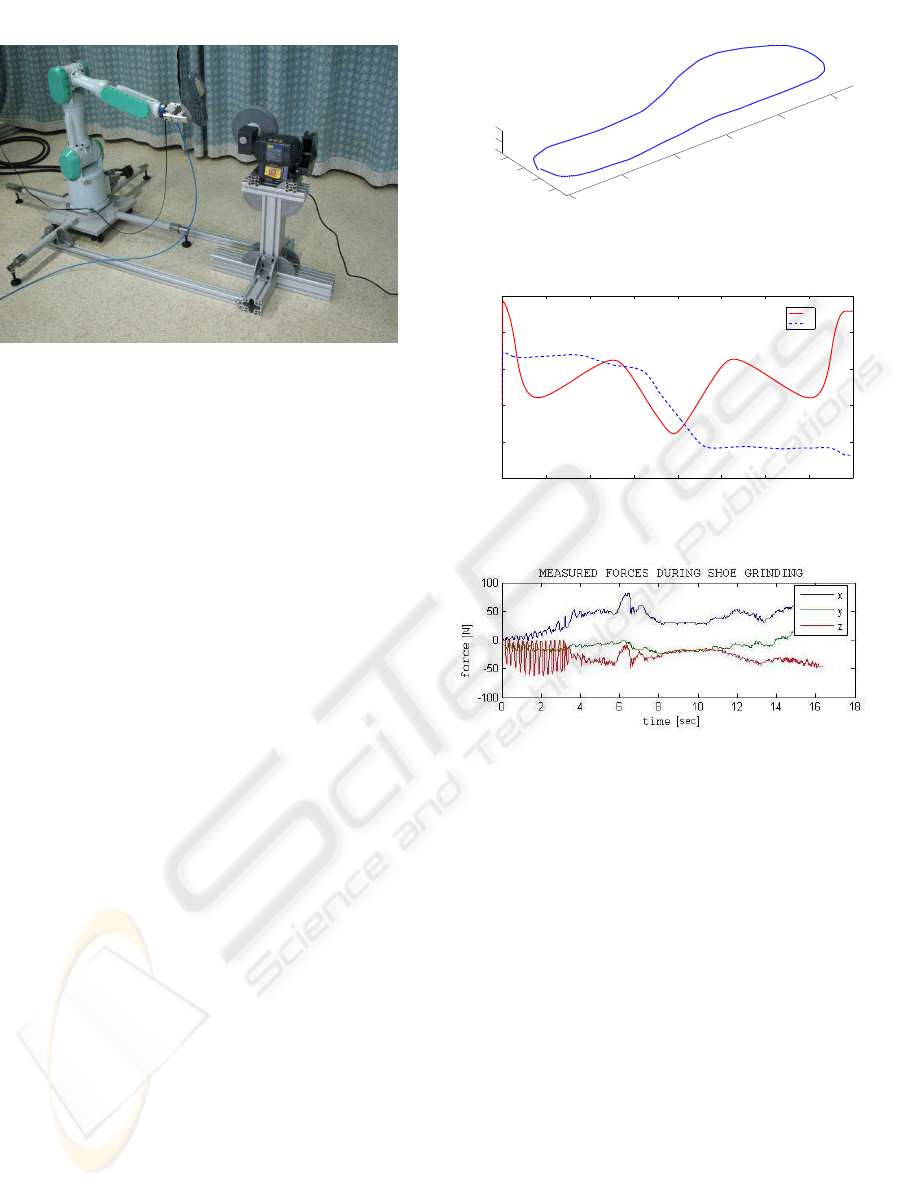
Figure 3: Experimental cell for shoe bottom roughing.

The prototype of the cell is shown in ﬁgure

3. It consists of the Mitsubishi Pa10 robot with a

force/torque sensor Jr3 mounted in the robot wrist, a

grinding machine, a Pa10 robot controller and a cell

control computer, which coordinates the task and cal-

culates the required robot torques. The control com-

puter is connected to the robot controller using Arc-

Net. The frequency rate of the control algorithm (Eq.

9) and the motion optimization algorithm (Eq. 15)

is 700 Hz. The grinding path is obtained from CAD

model of the shoe. For this purpose, the control com-

puter is connected to the shoe database computer us-

ing Ethernet. Unfortunately, CAD model itself can

not supply all necessary data for the grinding process.

CAD models are usually available for the reference

shoe size, therefore, non-linear grading of the shoe

shape is necessary for the given size. Additionally,

some technological parameters such as material char-

acteristics and shoe sole gluing technology have to

be taken into account during the grinding trajectory

preparation. For this purpose, we have developed a

special CAD expert program, which enables the op-

erator to deﬁne additional technological and material

parameters. The program then automatically gener-

ates the grinding trajectory.

In order to show the efﬁciency of the proposed al-

gorithm, we deﬁned the shoe grinding trajectory as

seen in the Fig 4. Note that without using trajectory

optimization is is very hard to execute the given task

without splitting the desired trajectory in two or more

fragments. Fig 5 shows how the system rotated joints

of virtual mechanism in order to avoid the joint lim-

its and to minimize joint velocities of the robot and

virtual mechanism.

Similar behavior could be obtained also by using

the well known hybrid force-position control, where

restricted coordinates are perpendicular to the grind-

ing disc. However, the approach with hybrid force-

position control has several disadvantages. First of

−50

100

150

200

−20

100

110

Figure 4: Shoe grinding trajectory.

0 2 4 6 8 10 12 14 16

−10

−5

VIRTUAL JOINTS q(8) and q(9)

time(s)

angle(deg)

Figure 5: Virtual mechanism angles q8 and q9.

Figure 6: Resulting forces during the shoe grinding.

all, it requires perfect force tracking in order to main-

tain the tool always perpendicularto the grindingdisc.

Due to the irregularities of the shoe bottom and the

griding disc rotation, this is very hard to obtain. Re-

sults of the force tracking shown in Fig. 6 clearly

demonstrates, that the resulting force tracking is still

imperfect despite of the high sampling frequency of

the control algorithm. Note that only the force in z

direction was controlled in this case. On the contrary,

our approach does not require force control to follow

the shape of the grinding disc at all. Therefore, we

were able to apply the impedance control law, which

is more appropriate for the applications such as grind-

ing and polishing.

6 CONCLUSIONS

In the paper we presented a cell for shoe grinding op-

eration. We proposed a new method of solving the

kinematic redundancy which arises from the shape

SHOE GRINDING CELL USING VIRTUAL MECHANISM APPROACH

163

of the work tool. The main beneﬁt of the proposed

method is the simplicity and efﬁciency. It can be

used on the existing robot controllers with very mod-

erate changes of the control algorithm. The proposed

method can be applied even in the case of moving ob-

stacles during the task execution, assuming that the

shape and position of the obstacle is known. Another,

perhaps for the practical implementation even more

attractive possibility is to use the proposed approach

in the trajectory generation and not in the control al-

gorithm. In this case we can use existing standard in-

dustrial robots and we beneﬁt from the the advantages

of the kinematic redundancy due to circular shape of

the tool. This latter approach was successfully im-

plemented in the cell for custom ﬁnishing operations

in shoe assembly (Nemec and Zlajpah, 2008). It was

also demonstrated that the proposed control has many

advantages when compared with the hybrid force-

position control, which tracks an unknown shape us-

ing only the force sensor data.

REFERENCES

Asada, H. and Slotine, J.-J. (1986). Robot Analysis and

Control. John Wiley & Sons.

Chaumette, F. and Marchand, . (2001). A redundancy-based

iterative approach for avoiding joint limits: Appli-

cation to visual servoing. In IEEE Transactions on

Robotics and Automation, 17(5).

Dulio, S. and Boer, S. (2004). Integrated production plant

(ipp): an innovative laboratory for research projects in

the footwear ﬁeld. In Int. Journal of Computer Inte-

grated Manufacturing, 17(7) : 601-611.

Jatta, F., Zanoni, L., Fassi, I., and Negri, S. (2004). A rough-

ing/cementing robotic cell for custom made shoe man-

ufacture. In Int. J. Computer Intergrated Manufactur-

ing, 17(7) : 645–652.

Khatib, O. (1986). Real-time obstacle avoidance for ma-

nipulators and mobile robots. In Int. J. of Robotic Re-

search, 5 : 90 – 98.

Khatib, O. (1987). A uniﬁed approach for motion and force

control of robot manipulators:the operational space

formulation. In IEEE Trans. on Robotics and Automa-

tion, 3(1) : 43 – 53.

Nemec, B. and et all (2003). Technology fostering indi-

vidual, organisational, and regional development: an

international perspective.

Nemec, B. and Zlajpah, L. (2000). Null velocity control

with dinamically consistent pseudo-inverse. In Robot-

ica, 18 : 513 – 518.

Nemec, B. and Zlajpah, L. (2001). Experiments with force

control of redundant robots in unstructured environ-

ment using minimal null-space formulation. In Jour-

nal of Advanced Computational Intelligence, 5(5) :

263 – 268.

Nemec, B. and Zlajpah, L. (2008). Robotic cell for custom

ﬁnishing operations. In Int. J. Computer Intergrated

Manufacturing, 21(1) : 33–42.

Nemec, B., Zlajpah, L., and Omrcen, D. (2007). Compar-

ison of null-space and minimal null-space control al-

gorithms. In Robotica, 2007, 25(5):511–520.

Nenchev, D. N. (1989). Redundancy resolution through lo-

cal optimization: A review. In J. of Robotic Systems,

6(6) : 769 – 798.

Oh, Y., Chung, W., Youm, Y., and Suh, I. (1998). Exper-

iments on extended impedance control of redundant

manipulator. In Proc. IEEE/RJS Int. Conf. on Intelli-

gent Robots and Systems, : 1320 – 1325, Victoria.

Park, J., Chung, W., and Youm, Y. (2002). Characterization

of instability of dynamic control for kinematically re-

dundant manipulators. In Proc. IEEE Conf. Robotics

and Automation, : 2400 – 2405, Washington DC.

Taylor, P. and Taylor, G. (1988). Garments and Shoe Indus-

try Robots.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

164