MODIFIED LOCAL NAVIGATION STRATEGY FOR

UNKNOWN ENVIRONMENT EXPLORATION

Safaa Amin, Andry Tanoto, Ulf Witkowski, Ulrich Rückert

System and Circuit Technology, Heinz Nixdorf Institute, Paderborn University

Fuerstenallee 11, D-33102 Paderborn, Germany

Saied Abdel-Wahab

Faculty of Computer and Information Sciences, Ain Shams University, Cairo, Egypt

Keywords: Exploration, Mini-robot Khepera, Teleworkbench.

Abstract: This paper presents an algorithm for unknown environment exploration based on the local navigation

algorithm (LNA). The original LNA doesn’t take into account the case in which the robots are trapped and

stop exploring the environment. In this paper, we propose some modifications to overcome this problem and

demonstrate it by using real robots. For validation purpose, we ran several experiments using the mini-robot

Khepera II running on the Teleworkbench. The complete environment is divided into small quadratic

patches with some objects placed in it representing obstacles. With on-board infrared sensors and wheel

encoder, the robot can successfully explore the unknown environment. Moreover, by calculating the

distance to surrounding patches, the implemented algorithm will minimize the distance traveled, and in turn

of the consumed energy and time. This paper also shows the advantage of using the Teleworkbench for

performing experiments using real robots.

1 INTRODUCTION

Exploration of unknown environments is one of

important problems in robotics. The goal of the

exploration task is to cover the whole environment

in a minimum amount of time or with minimum

consumed energy depending on the application.

Exploration approaches focus on guiding the robot

efficiently through the environment in order to build

a map. Exploration algorithms using either a single

or a multi-robot system based on simulations have

been studied extensively in the past (Stachniss,

2006, Simmons, 2000, Manolov, 2003, and Burgard,

2000). In this paper we present the result of the

implementation of local navigation algorithm (LNA)

for environment exploration as introduced in

(Manolov, 2003, Amin, 2007). We also modify the

LNA to solve the problem of trapped robot so that it

can explore the whole environment successfully

independent of its shape and the position of the

obstacles. Moreover, we use the distance of the

neighbouring patches relative to the current robot

position to further improve the algorithm. We also

demonstrate the implementation of the modified

algorithm using the mini-robot Khepera II.

Furthermore, we demonstrate the advantage of using

the Teleworkbench (Tanoto, 2005) as a test bed for

performing and analysing experiments with real

robots. For experiment analysis, we have developed

a graphical analysis tool based on the MPEG-4

video standard (Tanoto, 2006). This tool allows us

to record a video of the experiments together with

experimental data and to visualize the internal and

external behaviour of robots.

The paper is organized as follows: after presenting

related work, Section 3 describes the LNA for

unknown environment exploration and its limitation.

Our modified algorithm (MLNA) is presented in

Section 4. After that we present a comparison result

between the two algorithms using the mini-robot

Khepera II on the Teleworkbench. Finally, Section 6

concludes the paper.

171

Amin S., Tanoto A., Witkowski U., Rückert U. and Abdel-Wahab S. (2008).

MODIFIED LOCAL NAVIGATION STRATEGY FOR UNKNOWN ENVIRONMENT EXPLORATION.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 171-176

DOI: 10.5220/0001481801710176

 SciTePress

2 RELATED WORK

Exploration is the task of guiding a vehicle in such a

way that it covers the environment with its sensors.

Efficient exploration strategies are also relevant for

surface inspection, mine sweeping, or surveillance

(Choset, 2001). In the past, several strategies for

exploration have been developed. One group of

approaches deals with the problem of simultaneous

localization and mapping (Bourgoult, 2002). A

common technique for exploration strategies is to

extract frontiers between known and unknown areas

(Edlinger, 1994, Yamauchi, 1999) and to visit the

nearest unexplored place. These approaches only

distinguish between scanned and un-scanned areas

and do not take into account the actual information

gathered at each view-point. To overcome this

limitation (Gonzales, 2001) determine the amount of

unseen area that might be visible to the robot from

possible view-points. To incorporate the uncertainty

of the robot about the state of the environment

(Moorehead, 2001) and (Bourgault, 2002) use

occupancy grids (Hans, 1985) and compute the

entropy of each cell in the grid to determine the

utility of scanning from a certain location. (Whaite,

1997) present an approach that also uses the entropy

to measure the uncertainty in the geometric structure

of objects that are scanned with a laser range sensor.

In contrast to the work described here they use a

parametric representation of the objects to be

scanned. (Edlinger, 1994) developed a hierarchical

exploration strategy for office environments. Their

approach first explores rooms and then traverses

through doorways to explore other parts of the

environment. (Tailor, 1993) describe a system for

visiting all landmarks in the environment of the

robot. Their robot maintains a list of unvisited

landmarks that are approached and mapped by the

robot. (Dudek, 1991) propose a strategy for

exploring an unknown graph-like environment.

Their algorithm does not consider distance metrics

and is designed for robots with very limited

perceptual capabilities. Recently, Koenig has shown,

that a strategy, which guides the vehicle to the

closest point that has not been covered yet, keeps the

travelled distance reasonably small (Koenig, 2001).

However, as experiments reported in this paper

illustrate, such techniques can lead to a serious

increase of measurements necessary to build an

accurate map if the robot is not able to incorporate

measurements on-the-fly while it is moving. This

might be the case, for example, for robots extracting

distance information from camera images.

3 LOCAL NAVIGATION

STRATEGY

FOR ENVIRONMENT

EXPLORATION

The exploration strategy has to ensure that the

complete area is explored. The LNA computes only

the next step for moving. The computation is

dependent on the area around the robot (Manolov,

2003).

The exploration algorithm works as follows. The

complete environment is divided into small

quadratic patches. The robot starts the exploration

from any position in the environment. It can move

between patches in all directions (east, west, north,

south, and diagonal). When the robot visits a certain

patch, it is considered to be analyzed. For the

computation of the next movement, an algorithm is

used to determine the costs of reaching each free

patch around the robot. The cost function C for a

free patch P is given as:

C (P) =N (P) (1)

Where N (P) is a function that computes the number

of free neighbouring patches around patch P. A

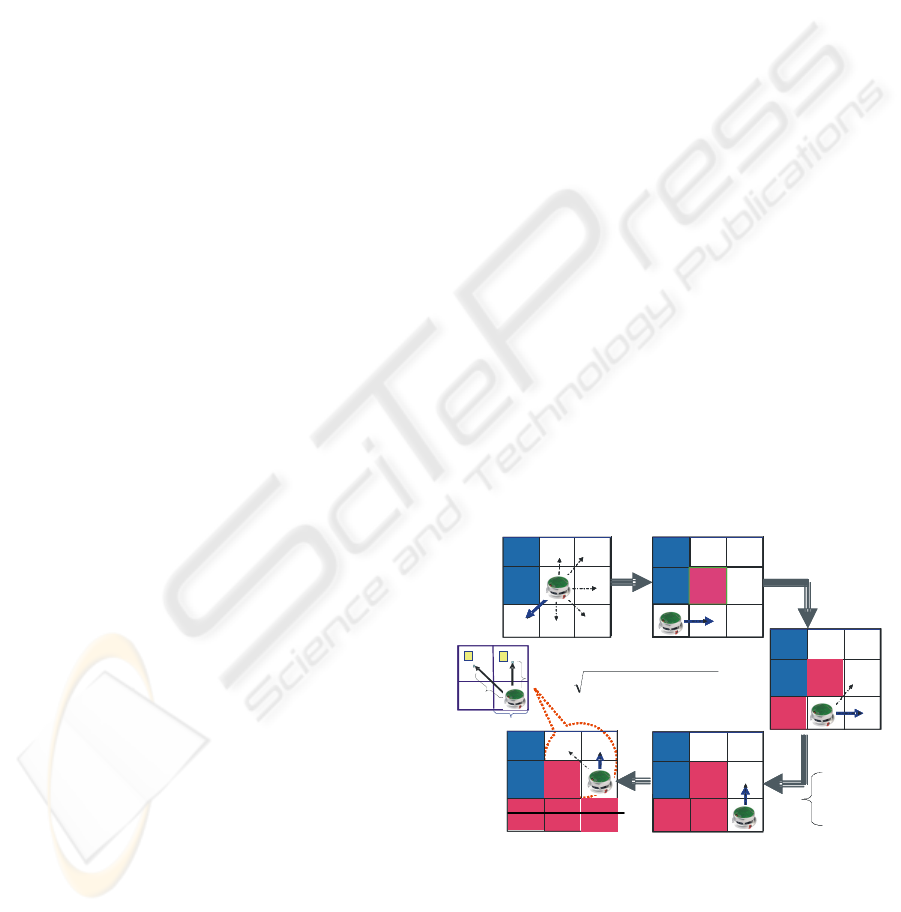
visualization of the evaluation is given in Figure 1.

After evaluating the cost for all free patches around

the robot, the robot moves to the patch with the

lowest cost that has the lowest number of neighbours

and which is therefore most unlikely to be reached

again in the future

(Manolov, 2003).

Obstacle

Wa ll

C(P)=2

C(P)=3C(P)=1

C(P)=2

C(P)=4

C(P)=2

C(P)=1

C(P)=3

C(P)=2

C(P)=1

C(P)=2

()

)12(12

YYxxD

−+−=

Wall

Explored

Wa ll

Explored

Wall

Wa ll

Explored

ExploredExplored

Explored

Status=

Unexplored

ExploredExplored

WallWall

Obstacle

Wa ll

C(P)=2

C(P)=3C(P)=1

C(P)=2

C(P)=4

C(P)=2

C(P)=3C(P)=1

C(P)=2

C(P)=4

C(P)=2

C(P)=1

C(P)=3

C(P)=2

C(P)=1

C(P)=2

()

)12(12

YYxxD

−+−=

Wall

Explored

Wa ll

Explored

Wall

Wa ll

Explored

ExploredExplored

Explored

Status=

Unexplored

ExploredExplored

WallWall

Status=

Unexplored

ExploredExplored

WallWall

Figure 1: The algorithm determines for each free patch

around the robot the costs C to reach it. The costs of all

neighboring patches are different. Two patches have the

same cost. The distance between the robot and the

neighboring patches which have the same minimum costs

(patch 1 and patch 2).

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

172

However, it is possible that there exist more than

one patch with the same minimum cost. To solve

this problem, we improve the algorithm by taking

also into consideration the distance between the

robot and each one of these patches, and then select

the patch with minimum distance. Figure 1

illustrates the aforementioned situation.

4 THE MODIFIED LOCAL

NAVIGATION ALGORITHM

(MLNA)

LNA has a draw back that it can’t ensure

completeness in the case of a robot being trapped,

e.g. when all of its neighbors are either obstacles or

explored, and there is no free cell around to compute

its cost. In this situation, it will simply stop and fails

to complete exploring the whole environment as

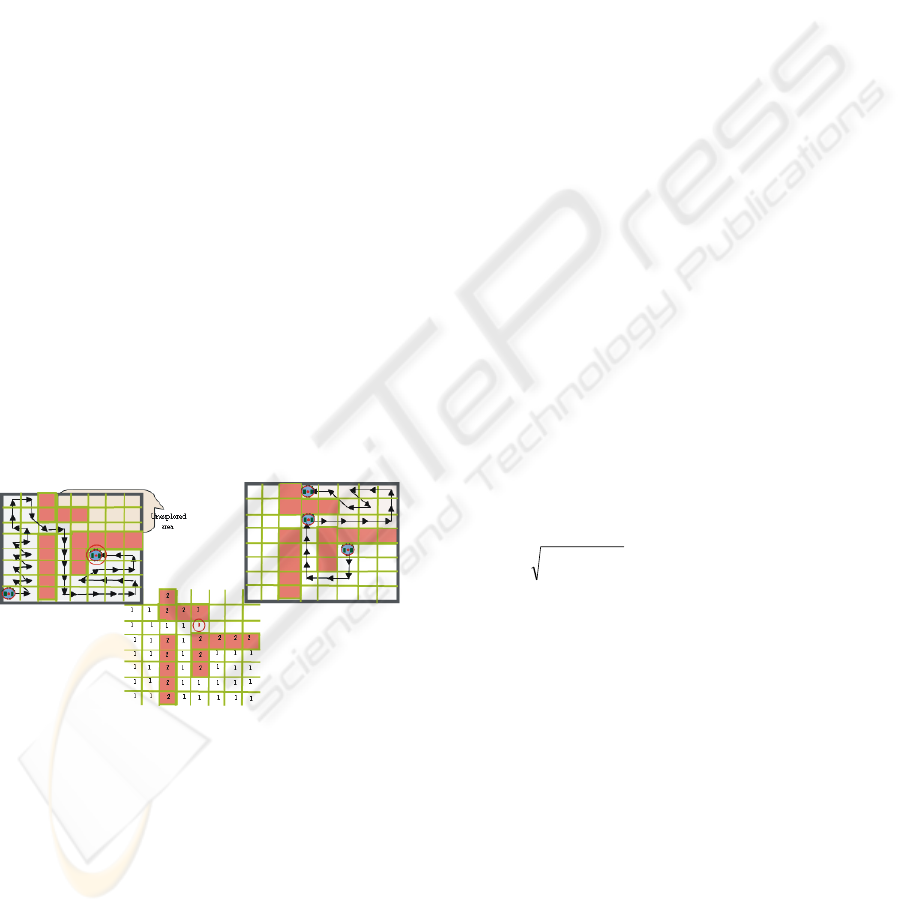
illustrated in Figure 2a.

We modified the algorithm to overcome this

problem by calculating the shortest path to reach the

unexplored area and continue exploring the

environment. Our modified algorithm will determine

the cost for reaching all the un-explored cells. We

use the occupancy grid map in our algorithm to

describe the environment. As illustrated in Figure 2b

a cell can be in one of the following states which are

represented by an integer number:

(a) (b) (c)

Figure 2: (a) the trapped robots Problem in LNA. (b) The

map associated to the environment. (c) The shortest path

that the robot follows to reach to the unexplored area and

complete the exploration task.

Unexplored (0). No robot has been in the cell yet.

As shown in Figure 2b, the cell with state 0 is

detected by Khepera sensors as an unexplored free

cell.

Explored (1). The cell has been traversed at least

once by the robot, but it might need to go through it

again in order to reach unexplored regions. It also

means that the cell is free.

Wall (2). The cell cannot be traversed by the robot

because it is blocked by an obstacle or a wall.

We had to differentiate between the explored cells

that contain an obstacle and the explored cells that

are empty, in order to be able to identify the back

path of the robot successfully if required.

4.1 Cost of Reaching a Target Location

To determine the cost of reaching the Frontier cells,

which are the cells between known and unknown

areas, we compute the optimal path from the current

position of the robot to these cells based on a

deterministic variant of the value iteration (Eq. (3)).

In the following, c

x,y

corresponds to the x-th cell in

the direction of the x-axis and the y-th cell in

direction of the y-axis of the two-dimensional

occupancy grid map. In our approach, the cost for

traversing a grid cell c

x,y

is proportional to its

occupancy value p(c

x,y

). The minimum cost path is

computed using the following two steps:

1. Initialization. The grid cell that contains the

robot location is initialized with 0, all others

with∞.

(2)

2. Update Loop. For all grid cells C

x,y

do:

(3)

Where occ

max

is the maximum occupancy

probability value of a grid cell the robot is allowed

to traverse. This technique updates the value of all

grid cells by the value of their best neighbours, plus

the cost of moving to this neighbour. Here, cost is

equivalent to the probability p(c

x,y

) that a grid cell

x,y

is occupied times the distance to the cell. The

update rule is repeated until convergence. Then each

value T

x,y

corresponds to the cumulative cost of

moving from the current position of the robot to c

x,y

The convergence of the algorithm is guaranteed as

long as the cost for traversing a cell is not negative

and the environment is bounded. Both criteria are

fulfilled in our approach.

robottheofpositiontheisyxif

otherwiseyx

),(,0

{

∞

]

max

,0[)

(}1,0,1{,|

)

{min

occ

yyxx

CPyx

yyxx

CPyx

yyxx

∈

Δ+Δ+

∧−∈ΔΔ

Δ+Δ+

Δ+Δ

Δ+Δ+

MODIFIED LOCAL NAVIGATION STRATEGY FOR UNKNOWN ENVIRONMENT EXPLORATION

173

The resulting cost function T can also be used to

efficiently derive the minimum cost path from the

current location of the robot to arbitrary goal

positions c

x,y

. This can be done by steepest descent

in T, starting at c

x,y.

As shown in Figure 2c the

algorithm will calculate the shortest path to the

unexplored cell. As soon as the robot reaches this

cell, it will complete exploring the environment

using the cost equation (1).

5 EXPERIMENT USING THE

MINI-ROBOT KHEPERA

To test the implemented exploration algorithm with

real robot, we use the Teleworkbench. We built the

environment on one small field (1 meter x 1 meter).

We use Lego bricks to form the environment. As the

robot platform we use mini-robot Khepera II

http://www.k-team.com. Its dimension is 5 cm in

diameter with one on-board microcontroller. The

robot’s base module is equipped with eight infrared

sensors. The maximum detection range using the

Khepera II basic setting. Up to 7cm distance. One of

the advantages of this robot is that it is extensible,

which means that diverse auxiliary modules can be

added on top of it. To allow longer runtime and

wireless communication, we extend the robot with

our extension module consisting of an additional,

battery and a Bluetooth chip. With this module, the

robot can operate up to 3 hours continuously.

5.1 Teleworkbench

The Teleworkbench is a teleoperated platform and

test bed for managing experiments using mini-robots

(Tanoto, 2005). The system is accessible via the

Internet. Through the web-based user interface, local

or remote users can schedule experiments and set

programs to be downloaded to each individual robot.

Via a Bluetooth module, robots can exchange

messages to each other or to the Teleworkbench

Server wirelessly. During experiments, the video

server tracks the robots on the field to provide

position and orientation of the robots. In parallel,

this data will be stored locally and streamed

simultaneously as live-video via the Internet.

For experiment analysis purpose, we developed a

graphical analysis tool based on the MPEG-4 video

standard (Tanoto, 2006). This tool allows us to

visualize the internal and external behaviour of

robots. With this tool, the recorded video of the

experiment can be displayed together with some

computer-generated objects representing important

information, e.g. robot path, sensors’ value, or

exchanged messages. Moreover, users can

interactively control the appearance of those objects

during runtime. The Teleworkbench can use

different types of mini-robots, such as Khepera II, as

its robotic platform.

5.2 Algorithm Implementation

Based on the aforementioned algorithm, we develop

the robot program in C language. The goal of the

experiment is to explore an unknown bounded-

environment of size 1 meter square. We divided the

environment into 8 x 8 patches, each of which has a

dimension of 0.125 x 0.125 m

as shown in Figure

3c. To detect obstacles or walls and their distance

relative to the robot, we use robot’s on-board

infrared sensors. Thus, if an object is detected, the

robot marks the patch with the object as occupied.

Moreover, the robot gets its position by using

odometry.

5.3 Experiment Setup and Execution

After code compilation, we download the program

remotely via the Teleworkbench web-based user

interface. During testing, we ran several experiments

with different parameters, such as varying the

threshold for the infrared sensors, etc. this is needed

due to hardware unideality that is not taken into

account during simulation. We did each experiment

as follows: select a robot, download the program,

turn on the webcam in record mode, free the robot

after the experiment is over, and save the video data

and the log files to be used for analysis. After each

experiment, we ran the post experiment analysis tool

which will generate an MPEG-4 video with the

video of the experiment and the robot path as well as

some colour tiles representing the patches.

5.4 Experimental Result

Experiments had been executed with the same

environment setting and initial position. The result

shows that by using the LNA the robot could explore

all the free patches in the environment as shown in

Figure 3a. But if the environment appears as shown

in Figure 3b, the robot stops when it finds that all its

neighbours are either explored or wall. But when

applying the MLNA the robot could successfully

explore all the free patches in the environment.

Moreover, it could detect obstacles and walls

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

174

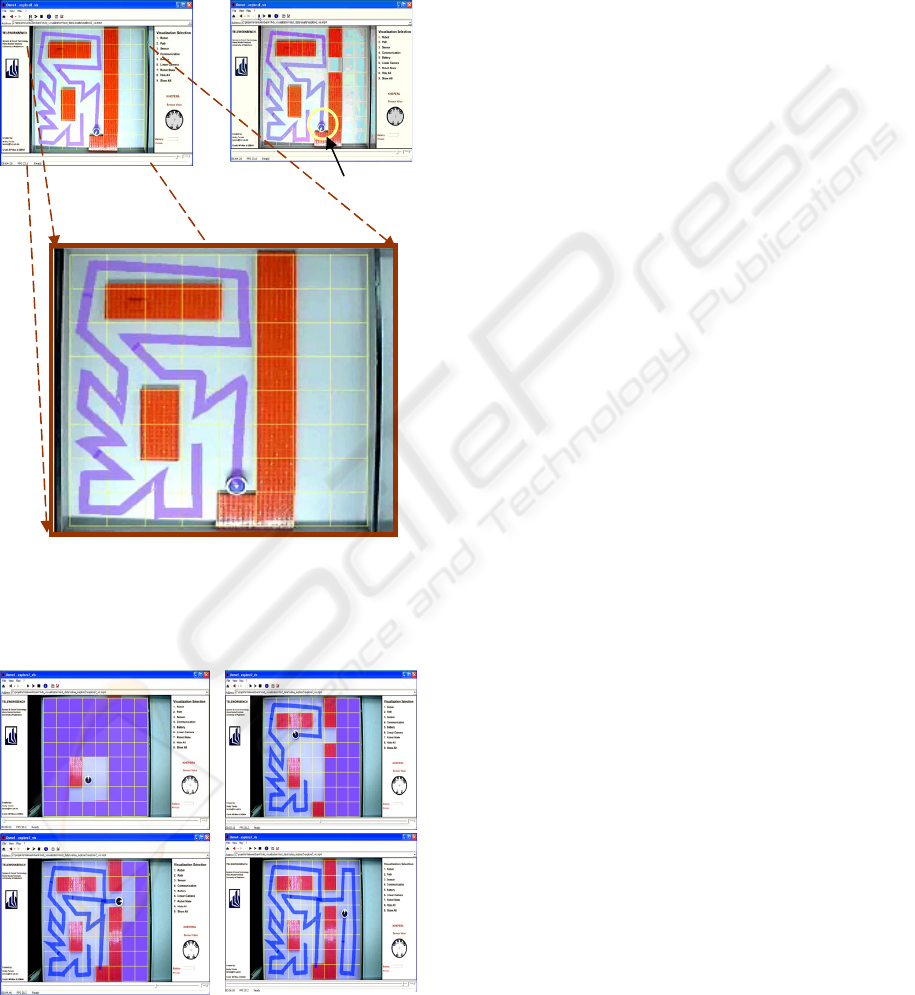
robustly by using only its on-board infrared sensors

as shown in right image in Figure 4.

The MPEG-4 video played-back on OSMO4

video player shows the path of the robot during the

experiment. If needed and available, other

information, such as sensors, internal state, etc, can

also be displayed.

Figure 3: (a) Snapshots of the video visualizing the

exploration experiment using LNA. (b) The trapped robot

problem in LNA. (c) Zooming on the environment

Figure 4: Snapshots of the video visualizing a step by step

exploration experiment of an unknown environment using

the MLNA.

However, we can see that the robot path deviates

when it travelled from one patch to the other, as

shown in Figure 3 and Figure 4. This is mainly due

to the error generated by odometry. As a result, in

some occasions the robot collided with obstacles or

walls during its movement. Another interesting point

from the experiment is that there is one occasion in

which the robot had to select one of two patches

with the same minimum cost (top-left image in

Figure 4). By using the distance calculation

(sec.4.1), the robot chose the patch exactly below it

because of its shorter relative distance to the current

robot position compared to the one of other cells.

6 CONCLUSIONS

In this work the modified local navigation strategy

for static unknown environment exploration has

been implemented and tested using the mini-robot

Khepera running on the Teleworkbench.

Experiments presented in this paper demonstrate that

the modified exploration algorithm is able to cover

successfully the whole unknown environment and

overcome the draw back in LNA. Moreover, by

taking into consideration the distance of

neighbouring cells to the current robot position, the

robot always select the cells with minimum distance,

thus less energy and time. We notice also the

weakness of odometry to provide the robot’s

position. To improve it, we plan to get more robust

position information from the Teleworkbench.

Moreover, varying environment setups and initial

locations are necessary to prove the robustness of

the algorithm.

ACKNOWLEDGEMENTS

This work is a result of common research between

the System and Circuit Technology, Heinz Nixdorf

Institute, University of Paderborn and Scientific

Computing Department, Faculty of Computer and

Information Sciences, Ain Shams University.

cultural department and study mission. This work

was partly supported by the Sixth Framework

Programme of the European Union as part of the

GUARDIANS project (no. 045269).

The robot stops here

(a)

(b)

(c)

MODIFIED LOCAL NAVIGATION STRATEGY FOR UNKNOWN ENVIRONMENT EXPLORATION

175

REFERENCES

Stachniss, C., 2006. Exploration and Mapping with

Mobile Robots. PhD Thesis, Albert-Ludwigs-

University, Freiburg, Germany.

Simmons, R., Apfelbaum, D., Burgard, W., Fox, D.,

Moors, M., Thrun, S., and ounes, H., 2000.

Coordination for multi-robot exploration and mapping.

In AAAINational Conference on Artificial Intelligence,

Austin, TX, USA.

Manolov, Ognyan; Iske, Burkhard; Noykov, Sv.; Klahold,

Jürgen; Georgiev, G.; Witkowski, Ulf; Rückert, Ulrich

. 2003. Gard - An Intelligent System for Distributed

Exploration of Landmine Fields Simulated by a Team

of Khepera Robots. In Proceedings of the

International Conference Automatics and Informatics,

Sofia, Bulgaria.

S. Amin, A.Tanoto, U. Witkowski, U. Rückert, M. S.

Abdel-Wahab, 2007. Environment Exploration Using

Mini-Robot Khepera, In Proceedings of the, 4

International Symposium on Autonomous Mini-robots

for Research and Edutainmen (AMiRE 2007), Buenos

Aires, Argentina.

Burgard, W., Fox, D., Moors, M., R. Simmons and Thrun.,

S., 2000. Collaborative Multi-Robot Exploration, In

Proc. Intl. Conf.on Robotics and Automation, San

Francisco.

Tanoto, A., Witkowski, U., Rueckert, U. (2005)

Teleworkbench: A Teleoperated Platform for Multi-

Robot Experiments, In Proceedings of the 3rd

International Symposium on Autonomous Mini-robots

for Research and Edutainment (AMiRE 2005), Fukui,

Japan.

Tanoto, A., Du, J., Kaulmann, L., Witkowski, U., 2006.

MPEG-4-Based Interactive Visualization as an

Analysis Tool for Experiments in Robotics, In

Proceeding of the 2006 International Conference on

Modeling, Simulation and Visualization Methods, Las

Vegas, USA.

Choset, H. Coverage for robitics - a survey of recent

results. 2001. Annals of Mathematics and Artifical

Intelligence.

Bourgoult, F, Makarenko, A, Williams, B, Grocholsky, B.,

and DurrantWhyte, F., 2002. Information based

adaptive robotic exploration. In Proc. of the IEEE/RSJ

Int. Conf. on Intelligent Robots and Systems (IROS).

Edlinger, T, and Puttkamer, E., 1994. Exploration of an

indoor-environment by an autonomous mobile robot.

In Proc. of the IEEE/RSJ Int. Conf. on Intelligent

Robots and Systems (IROS).

Yamauchi, B., Schultz, A. and Adams, W., 1999.

Integrating exploration and localization for mobile

robots. Adaptive Systems, 7(2).

Gonz´alez, H. Ba˜nos, H, and Latombe, J, 2001.

Navigation strategies for exploring indoor

environments. International Journal of Robotics

Research.

Moorehead, S, Simmons, R, and Whittaker, W., 2001.

Autonomous exploration using multiple sources of

information. In Proc. of the IEEE Int. Conf. on

Robotic.

Hans P. Moravec and Elfes, A., 1985. High resolution

maps from wide angle sonar. In Proc. IEEE Int. Conf.

Robotics and Automation.

Whaite, P and Ferri, F., 1997.Autonomous exploration:

Driven by uncertainty. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 19(3):193– 205

Tailor, C and Kriegman, D., 1993. Exloration strategies

for mobile robots. In Proc. of the IEEE Int. Conf. on

Robotics & Automation (ICRA), pages 248–253.

Dudek, G, Jenkin, M, Milios, E and Wilkes, D., 1991.

Robotic exploration as graph construction. IEEE

Transactions on Robotics and Automation, 7(6):859–865.

Koenig, S., Tovey, C., and Halliburton., W., 2001. Greedy

mapping of terrain. In Proc. Of the IEEE Int. Conf. on

Robotics & Automation (ICRA).

Makarenko, A., Williams, B., Bourgoult, ,F., and Durrant-

Whyte, F., 2002. An experiment in integrated

exploration. In Proc. of the IEEE/RSJ Int. Conf. on

Intelligent Robots and Systems (IROS), Lausanne,

Switzerland.

Stachniss, C., Hähnel, D., Burgard, W., and Grisetti, G.,

2005. On actively closing loops in grid-based

FastSLAM. Advanced Robotics.

Stachniss, C., and Burgard, W., 2005. Mobile robot

mapping and localization in nonstatic environments, In

Proc. of the National Conference on Artificial

Intelligence (AAAI),Pittsburgh, PA, USA.

Dissanayake, G., Newman,P., Clark, S., Durrant-Whyte,

F., and Csobra, M., 2001. A solution to the

simultaneous localization and map building (SLAM)

problem, IEEE Trans. on Robotics and Automation..

Choset, H., 2001. Topological simultaneous localization

and mapping (SLAM): Toward exact localization

without explicit localization. IEEE Transactionson

Robotics and Automation.

Moorehead, S., Simmons, R., and Whittaker,L., 2001.

Autonomous exploration using multiple sources of

information, In IEEE International Conference on

Robotics and Automation (ICRA ’01).

Stachniss, C, Burgard, W., 2003. Exploring unknown

environments with mobile robots using coverage

maps. In Proc. of the Int. Conf. on Artificial

Intelligence (IJCAI).

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

176