ONE MODIFICATION OF THE CUSUM TEST FOR DETECTION

EARLY STRUCTURAL CHANGES

Julia Bondarenko

Department of Economic and Social Sciences, Helmut-Schmidt University Hamburg

University of the Federal Armed Forces Hamburg, Holstenhofweg 85, 22043 Hamburg, Germany

Keywords:

CUSUM test for structural breaks, recursive residuals, power of test, mixture distribution, Monte Carlo simu-

lation.

Abstract:

Structural shifts in time series can occur as consequences of complex processes, arising in system. An ig-

norance of such structural changes can cause an associated regression model misspeciﬁcation. In practice,

early detection and response to outbreaks, causing the changes in a process, is highly important. The famous

CUSUM test of Brown, Durbin & Evans, has a poor power in detecting the structural breaks in parameters

occurring early (and also late) in the sample. In this paper, we propose CUSUM-similar test which, due to the

transformation of recursive residuals forces the detection of temporal dependence structure in linear regres-

sion model and has a larger power for the early structural breaks. Here our interest centres on the detection of

single breaks occurring in parameters of the linear model. Distribution and other probabilistic characteristics

of the transformed residuals are provided, the boundaries for the new test are derived. The new test can be

considered then as a complement to the standard CUSUM test.

1 INTRODUCTION

Structural shifts in time series can occur as con-

sequences of complex processes, arising in system

(Basseville and Nikiforov, 1993). An ignorance of

such structural changes can cause an associated re-

gression model misspeciﬁcation. The evidence of

the parameters instability in linear models can be

detected by the number of corresponding diagnos-

tic tests. Particularly, the famous and important of

them include ﬂuctuation tests, with the CUSUM and

CUSUMQ tests of Brown, Durbin & Evans (BDE

tests) (R. L. Brown and Evans, 1975), standing ﬁrst

on the list. These tests are easy for implement-

ing and based on the calculating of the cumulative

sums of recursive residuals (CUSUM) and the cu-

mulative sums of the squares of recursive residuals

(CUSUMQ) for regression. The CUSUM test is gen-

erally used to detect the systematic movements of pa-

rameters, whereas CUSUMQ test tends to capture the

sudden, haphazard movements.

A number of extensions of the standard BDE

CUSUM tests have been developed, like the CUSUM

and CUSUM of squares tests using OLS (ordinary

least squares) residuals instead of recursive resid-

uals (Proberger and Kraemer, 1992), the CUSUM

tests with lagged dependent variables in regression

(W. Proberger and Alt, 1989), the CUSUM tests with

non-stationary regressors (Inder and Hao, 1996), the

MOSUM and MOSUM of squares tests putting em-

phasis on moving averages rather than cumulative

sums (C.-S. J. Chu and Kuan, 1995a), the moving-

estimates test (C.-S. J. Chu and Kuan, 1995b), etc.

It is a well-known fact, that, CUSUM tests, both

with recursive and OLS residuals, have a poor power

in detecting the structural breaks in parameters occur-

ring early and late in the sample, as well as the ones

orthogonal to the mean regressor (see (W. Kraemer

and Alt, 1988); (Kraemer and Sonnberg, 1986), pp.

50-51; (Proberger and Kraemer, 1990); (Proberger

and Kraemer, 1992)). A modiﬁcation of recursive

residuals CUSUM test, which is robust to the later

problem, was proposed in (Luger, 2001). The rea-

son for earlier problem is that CUSUM has no chance

to cumulate for the such kind of breaks. In particular,

some improving, due to alternative test boundaries de-

veloping, was suggested, in (Zeileis, 2000) for OLS

CUSUM test.

In practice, early detection and response to out-

breaks, causing the changes in a process, is highly

important. In this paper, we propose a CUSUM-

similar test which, due to the transformation of re-

cursive residuals forces the detection of temporal de-

pendence structure in linear regression model and has

Bondarenko J. (2008).

ONE MODIFICATION OF THE CUSUM TEST FOR DETECTION EARLY STRUCTURAL CHANGES.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 18-22

DOI: 10.5220/0001482900180022

 SciTePress

a larger power for the early structural breaks. Here

our interest centres on the detection of single breaks

occurring in parameters of the linear model. Distri-

bution and other probabilistic characteristics of the

transformed residuals are also provided, the bound-

aries for the new test are derived. The new test can

be considered then as a complement to the standard

CUSUM test. The paper is organized as follows. Sec-

tion 2 presents the BDE’s original formulation of the

CUSUM test, discusses its main features. Section 3

offers our modiﬁcation of the CUSUM testing pro-

cedure. In the Section 4 we conduct comparison of

two tests via Monte Carlo simulation study. Section 5

summarizes and concludes.

2 STANDARD CUSUM TEST

Consider the linear regression model

= x

+ ε

, t = 1, ..., T , (1)

where y

is the tth observation of the dependent vari-

able, x

is the k ×1 vector of covariates at time t, β

are unknown parameters, and ε

are independent and

normally distributed with zero mean and variance σ

We are interested in testing for a discrete jump in at

least one of the β

at the unknown time point. The

null hypothesis can be formulated as

: β

= β, t = 1, ..., T , (2)

with alternative H

that at time T

∗

at least one of the

changes its value:

: β

= β, t = 1, ..., T

∗

< T ;β

6= β, t = T

∗

+1, ...,T.

(3)

The CUSUM test suggested by Brown, Durbin

and Evans (BDE) is a standard and commonly used

diagnostic test for this kind of situations. BDE’s

CUSUM test uses the standardized residuals deﬁned

−x

t−1

1 + x



t−1



−1

for t = k + 1, k + 2, ..., T,

(4)

where

t−1

is the OLS-estimator of β based on the

ﬁrst t −1 observations,

t−1



t−1



−1

t−1

, and X

t−1

and Y

t−1

are the (t −1) ×k and (t −1) ×1

matrices that obtain by stacking x

and y

, respec-

tively, for s = 1, 2, ...,t −1.

The advantage of working with w

s deﬁned by (4): it

can be shown, that under H

(2), they are independent

normally distributed with zero mean and variance σ

BDE CUSUM test is based on the cumulated sums of

standardized residuals:

∑

s=k+1

, (5)

where

σ is OLS-estimate of σ,

T −k

∑

s=k+1

We cannot obtain the explicit distribution of C

. But,

under null hypothesis of parameter stability, the ex-

pected value and variance of the statistic C

should be

equal to zero and the number of normalized residu-

als being summed. Hence, the continuous Brownian

motion process Z

can be considered as a good ap-

proximation of the discrete path of C

. Under H

the

sequence C

is thus a sequence of the approximately

normal variables, where E (C

) = 0, Var (C

) = t −k,

Cov (C

) = min(t,r) −k. Conﬁdence bounds for

the cumulated sums C

are then obtained by plot-

ting the two straight lines connecting the points k ±

√

T −k and T ±3a

√

T −k, where a is a parameter

depending on the α - signiﬁcance level chosen, and

is calculated on the basis of results for the Gaussian

process. Namely, a = 1.143 for α = 0.01; a = 0.948

for α = 0.05; a = 0.850 for α = 0.1 (see (R. L. Brown

and Evans, 1975)).

Unfortunately, the CUSUM test suffers from low

power, which decreases dramatically if the change

point is close to the early beginning or to the end of

the sample. In the next section we consider one mod-

iﬁcation of the CUSUM test based on the sconced cu-

mulative sums.

3 MODIFICATION OF CUSUM

TEST

Let’s take into account the temporal structure of the

residuals w

, and construct a new sequence of random

variables u

, t = k + 1, ..., T :

= w

+ c w

{

t−1

> 0

}

, w

= 0. (6)

where, as before, w

˜ N



0, σ



and independent, I

{

}

is indicator function, and c is some constant, c > 0,

which can be considered as a penalty magnitude for

upward or downward trends in CUSUM values. We

will obtain now a distribution of the variables u

Theorem. Let w

are independent identically dis-

tributed random variables, having a common symmet-

ric about zero distribution, where F

(x) is a probabil-

ity function, and c > 0. Then

ONE MODIFICATION OF THE CUSUM TEST FOR DETECTION EARLY STRUCTURAL CHANGES

(x) =



(x) +F



1 +c



. (7)

Proof. We can perform F

(x) as a sum of the fol-

lowing probabilities:

(x) = P [u

< x] = P [w

+ c w

{

t−1

> 0

}

< x] = (8)

P[w

+ c w

< x ; w

t−1

> 0] +

P[w

< x ; w

t−1

≤ 0].

For simplicity let’s consider two cases:

1) x ≤ 0. Then (8) can be written as:

P[w

+ c w

< x ; w

t−1

< 0] +

P[w

≤ x ; w

t−1

≥ 0] = P



1+c

; w

t−1

< 0



P[w

≤ x ; w

t−1

≥ 0] = F



1+c



(0) +

(x)(1 −F

(0)) = F



1+c



(0) + F

(x) −

(x)F

(0) =





1+c



+ F

(x)



2) x > 0. (8) has a form:

P[w

+ c w

< 0 ;w

t−1

> 0] +

P[0 ≤ w

+ c w

< x ; w

t−1

> 0]+

P[w

< x ; w

t−1

≤ 0] = P [w

< 0 ; w

t−1

< 0] +



0 ≤ w

1+c

; w

t−1

> 0



P[w

< x ; w

t−1

≤ 0] = F

(0)F

(0) +



1+c



−F

(0)



(0)+

P[w

< 0 ;w

t−1

≥ 0] + P [0 ≤w

< x ; w

t−1

< 0] =

(0)F

(0)+



1+c



−F

(0)



(0) + F

(0)(1 −F

(0)) +

(x) −F

(0))F

(0) =



1+c



−





(x) −







1+c



+ F

(x)



Thus, the CDF (PDF) of the random variables

is a mixture of two normal distributions. It fol-

lows from the Theorem that u

s have zero expectation,

E (u

) = 0, and variance Var (u

) =



1 +(1 + c)



The joint CDF function obtained can be obtained by

analogy with (7).

Covariance, C ov (u

, u

t+1

E [(u

−E (u

))(u

t+1

−E (u

t+1

))]=E (u

t+1

), equals

to zero. In addition, variables u

s have zero skewness

s(u

) = 0, and kurtosis κ(u

) =

[

1+(1+c)

]

(

1+(1+c)

)

, revealing

fatter tails.

The new statistic, which we will call ”penalized”

CUSUM (PCUSUM), can be written as following:

∑

s=k+1

∑

s=k+1

+ c

∑

s=k+1

{

s−1

> 0

}

(9)

where

T −k

∑

s=k+1

. It is follows from the prop-

erties of u

, that E





= 0 but

≥

σ, thus, we ex-

pect that the PCUSUM test has a chance to cumulate

well and to detect structural shifts only in very begin-

ning of the sample.

Like the original CUSUM test (5), the modiﬁed

test (9) is only an asymptotic test and has no any

certain distribution. Obviously, under c → 0, the

sequence C

k+1

, ...,C

may be approximated by the

Brownian motion process mentioned in Section 1, and

the bounds for cumulated sums C

are calculated then

as the ones for C

. But for larger values c this can not

be applied. Hence, we have here a subproblem of sim-

ulation of the presented test boundaries.

We will partially implement the techniques used

in (Tanizaki, 1995) for conﬁdence intervals calcula-

tion. The simulation algorithm may be carried out

as follows. Let us generate L replicates. In each

replicate i, i = 1, 2, ..., L, we simulate T −K random

variables u

i,t

, t = k + 1,k + 2,...,T , pairwise depen-

dent and uncorrelated, drawn from the mixture of

two bivariate normal distributions (7). Then the cu-

mulated sums, s

i,t

∑

s=k+1

i,s

, are calculated. At

the signiﬁcance level α we have for statistic (9) that

P[L

k+1

< C

k+1

< U

k+1

,...,L

< C

< U

] = 1 −α,

where L

and U

are correspondingly the lower and

upper bounds for the value C

, and



k+1

< C

k+1

< U

k+1

, ..., L

< C

< U







< C

< U



T −k

for any t = k + 1, ..., T , since C

are not indepen-

dent. Let assume that P



< C

< U



= 1 −α

and denote α = f (α

), where f is some unknown

function (in the case of independence one has f (x) =

1 −x

T −k

), which we will obtain by simulation. Ap-

plying the Newton-Raphson algorithm, we calculate

our α

following the scheme:

( j)

= α

( j−1)

+ d

( j)



α − f



( j−1)



where j is iteration number, d

( j)

= δd

( j−1)

with

δ = 0.5 and d

(0)

= 1, α

(0)

= α. The conver-

gence criterion is



( j)

−α

( j−1)



< 0.0001. Re-

peat, that the function f



( j)



is derived at jth it-

eration as following: f



( j)



equals to the num-

ber of sequences

i,k+1

, ..., s

i,T

i=1

within inter-

vals



i,k+1



( j)

,...,



i,T



( j)

divided by

L, where intervals



i,t



( j)

are obtained for

the value α

( j)

. Note, that unlike the standard

CUSUM statistic, which has symmetric lower and

upper boundaries, we don’t claim here L

= −U

for PCUSUM statistic. To be fair to the standard

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

CUSUM, we use a linear regression to obtain the lin-

ear boundaries from the curved ones:

= a

and

= a

+ a

t, where a

, a

are intercepts,

, a

are slopes,

are the best ﬁtting lines.

4 MONTE CARLO STUDY

In this section we present a Monte Carlo study of the

new CUSUM test in comparison with the classical

one. In order to see the performance of C

, we con-

sider the model (1), where the matrix of independent

variables x

has the following design:



1, (−1)



t=1

, (10)

which was also used in simulation study in (In-

der and Hao, 1996) and (Kraemer and Sonnberg,

1986). Values ε

, as before, are independent nor-

mal, generated with parameters 0 and 1. We sim-

ulate our responses y

for three sample sizes, T =

20 (small sample), T = 50 (medium sample) and

T = 500 (large sample), with β = [10, 2]

under the

null hypothesis of parameters constancy. The signif-

icance level α = 0.05, the computed empirical levels

for samples under c = {0.2; 0.5; 1.5} are cor-

respondingly α

{

0.0075; 0.0049; 0.0054

}

(T =

20), α

{

0.0055; 0.0036; 0.0029

}

(T = 50), α

{

0.0011; 0.0013; 0.0016

}

(T = 500).

Empirical (actual) test sizes, based on the simu-

lated data, at the nominal size of 5%, and c = {0.2;

0.5; 1.5} in PCUSUM test, are presented in the Table

1. Generally estimated sizes, calculated as rejection

rates under null hypothesis, with Monte-Carlo repli-

cations number N = 5000, are either below the nom-

inal size for CUSUM test, resulting in more ”liberal”

test, or almost equal to the nominal size. However,

the empirical sizes for PCUSUM test under c = 1.5

are larger than 0.05, declaring the more ”sensitive”

test.

Table 1: Empirical Sizes of the Tests, α = 0.05.

Test T = 20 T = 50 T = 500

CUSUM 0.0154 0.0276 0.0458

PCUSUM, c = 0.2 0.0338 0.0453 0.0476

PCUSUM, c = 0.5 0.0512 0.0510 0.0444

PCUSUM, c = 1.5 0.0686 0.0586 0.0646

Now, we introduce at time T

∗

= [λT ], where λ

can take any values between 0 and 1, some struc-

tural shift. Let’s consider a single structural shift

in parameters β is given by ∆β =

√

[cosφ, sinφ]

where φ is the angle between ∆β and mean regressor

r =



∑

t=1

∑

t=1



= [1, 0]

, b

is a constant

determining the intensity of the shift ,

∆β

√

We will take a number of different values of b

and φ,

namely, b

{

−12; −8; −6; −3; 3; 6; 8; 12

}

(pos-

itive and negative values, as we don’t claim the

boundaries of PCUSUM to be symmetric) and φ =

{

}

. In other words, we are testing two hypotheses:

: parameters are constant for 1 ≤ t ≤ T against

: parameters have two different constant values,

for 1 ≤t < T

∗

and T

∗

≤t ≤T .

It is possible to show that, as we have expected,

the linear boundaries for PCUSUM test become nar-

rower than CUSUM test boundaries only at the begin-

ning of the sample. Hence, it makes sense to choose

λ corresponding to the structural changes at the be-

ginning of the sample, λ = 0.3, for example. Empiri-

cal power was calculated as a probability that the test

statistic under the alternative hypothesis exceeded the

signiﬁcance threshold calculated from the distribution

under the null hypothesis (a frequency of the null hy-

pothesis rejection under the alternative hypothesis).

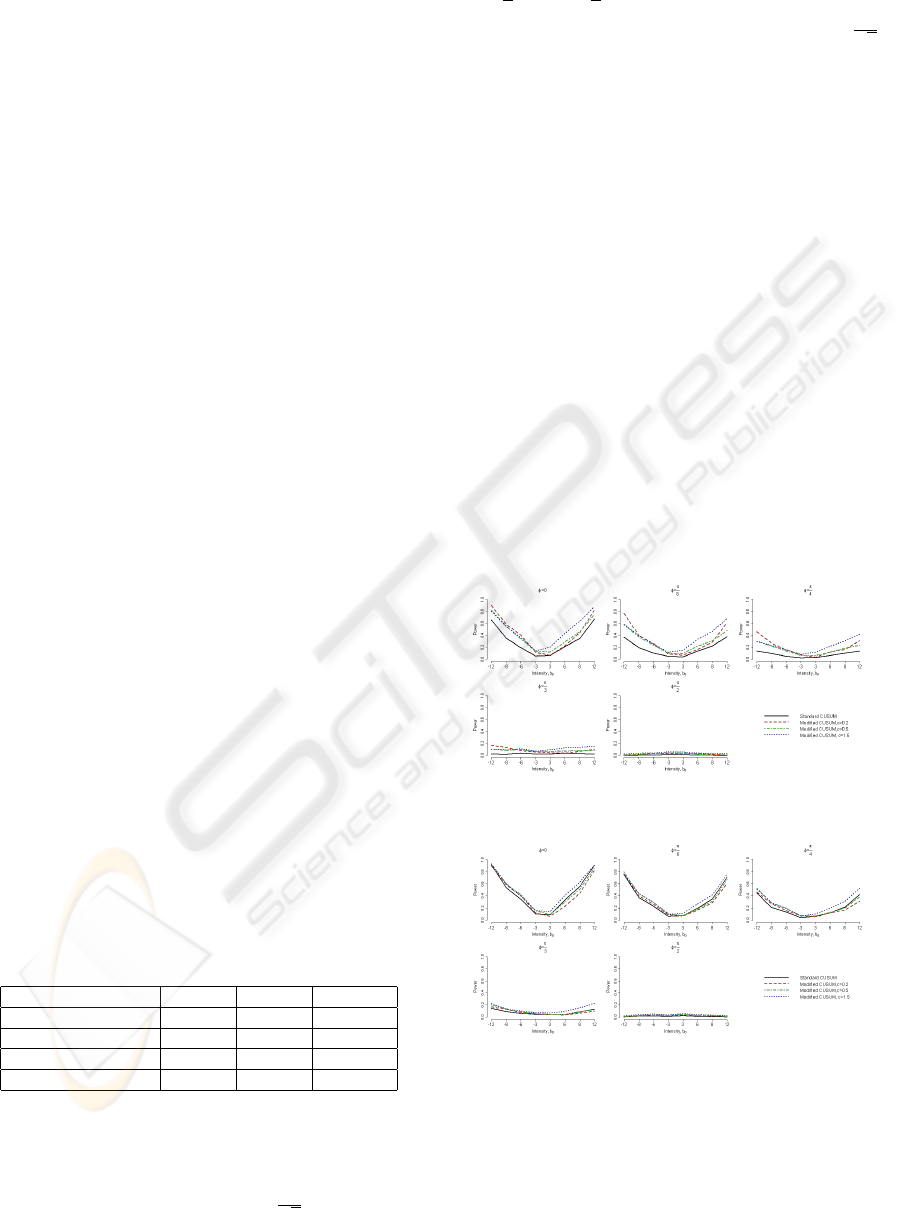
The obtained power plots, under N = 1000, λ = 0.3,

α = 5%, c ∈ {0.2; 0.5; 1.5} for T = 20, T = 50 and

T = 500 are presented on the Figures 1, 2 and 3, cor-

respondingly.

Figure 1: Power plots under T = 20, λ = 0.3.

Figure 2: Power plots under T = 50, λ = 0.3.

The obtained simulation results for the small sam-

ple with T = 20 reveal that the PCUSUM outper-

forms the CUSUM. For small values of shift inten-

sity b

and for φ = 90 this superiority is quite in-

sufﬁcient, for all samples. For the medium sample

T = 50, PCUSUM with c = 1.5 has higher power ev-

ONE MODIFICATION OF THE CUSUM TEST FOR DETECTION EARLY STRUCTURAL CHANGES

Figure 3: Power plots under T = 500, λ = 0.3.

erywhere, but PCUSUM with c = 0.5 and c = 0.2 -

only for negative values of b

. In big sample with

T = 500 an advantage is exhibited only by PCUSUM

with c = 1.5, for positive b

s. By virtue of the bound-

aries non-symmetry, the results are different for posi-

tive and negative values of b

also among PCUSUM

tests: for example, for T = 20 PCUSUM with larger

parameter c outperforms PCUSUM with smaller one

for positive b

s, but for negative b

s PCUSUM with

smaller value of c remains more effective.

5 CONCLUSIONS

In this paper we proposed a modiﬁed, based on the

penalized residuals, version of the standard BDE

CUSUM test for single structural breaks in parame-

ters of linear regression. The new test, PCUSUM,

is recommended as a complement to the standard

CUSUM test for better detecting the structural shifts

occurring early in the samples. Simulation results

have shown, that the modiﬁed CUSUM test has the

better chance to cumulate parameter breaks, occurred

at the beginning of the sample.

The subjects of eventual future research are:

• closer examination of properties of the PCUSUM

test boundaries, their comparison with derived

curved boundaries of the standard CUSUM test;

• adoption of the modiﬁed residuals (6) by CUSUM

of squares test (CUSUMQ) for testing structural

changes in variance (serial correlation and het-

eroscedasticity);

• appropriate transformation of the proposed new

test for both early and late structural breaks (in-

clusion of the more lagged residuals in (6), etc).

REFERENCES

Basseville, M. and Nikiforov, I. (1993). Detection of Abrupt

Changes - Theory and Application. Prentice Hall, En-

glewood Cliffs, NJ.

C.-S. J. Chu, K. H. and Kuan, C.-M. (1995a). Mosum tests

for parameter constancy. Biometrika, 82:603–617.

C.-S. J. Chu, K. H. and Kuan, C.-M. (1995b). The moving-

estimates test for parameter stability. Econometric

Theory, 11:669–720.

Inder, B. and Hao, K. (1996). A new test for structural

change. Empirical Economics, 21:475–482.

Kraemer, W. and Sonnberg, H. (1986). The Linear Regres-

sion Model under Test. Physica-Verlag, Heidelberg.

Luger, R. (2001). A modiﬁed cusum test for orthogonal

structural changes. Economic Letters, 73:301–306.

Proberger, W. and Kraemer, W. (1990). The local power of

the cusum and cusum of squares tests. Econometric

Theory, 6:335–347.

Proberger, W. and Kraemer, W. (1992). The cusum test with

ols residuals. Econometrica, 60:271–285.

R. L. Brown, J. D. and Evans, J. M. (1975). Techniques for

testing the constancy of regression relationships over

time. Journal of Royal Statistical Society B, 27:149–

163.

Tanizaki, H. (1995). Asymptotically exact conﬁdence inter-

vals of cusum and cusumq tests: a numerical deriva-

tions using simulation technique. Communications in

Statistics, 24:1019–1036.

W. Kraemer, W. P. and Alt, R. (1988). Testing for structural

change in dynamic models. Econometrica, 56:1355–

1369.

W. Proberger, W. K. and Alt, R. (1989). A modiﬁcation

of the cusum test in the linear regression model with

lagged dependent variables. Empirical Economics,

14:65–75.

Zeileis, A. (2000). p-values and alternative boundaries for

cusum tests. SFB Adaptive Information Systems and

Modelling in Economics and Management Science,

Working Paper 78.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics