
HYBRID WAVELET-KALMAN FILTER MULTI-SCALE
SEQUENTIAL FUSION METHOD
Funa Zhou
1,2
and Tianhao Tang
1
1.
Department of Electrical & Control Engineering, Shanghai Marintime University, Shanghai, China
2.
Computer&Information Engineering School, Henan University, Kaifeng, Henan, China
Keywords: Hybrid wavelet-Kalman filter, Sequential fusion, Non-
n
2
sampling.
Abstract: With the development of automation, multi-scale data fusion has become a hot research topic, however,
limited by the constraint that signal to implement wavelet transform must have the length of
q
2
, multi-scale
data fusion problem involved with non-
n
2
sampled observation data still hasn’t been efficiently solved. In
this paper, we develop a hybrid wavelet-Kalman filter multiscale sequential fusion method. First, we
develop the hybrid wavelet-Kalman filter multiscale estimation method which combines the advantage of
wavelet and Kalman filter to obtain the real time, recursive, multiscale estimation of the dynamic system.
Then, a multiscale sequential fusion method is presented. Under the hybrid wavelet-Kalman filter multiscale
estimation frame, we can easily fuse information from multiple sensors sequentially without designing other
complex fusion algorithm. The multiscale sequential fusion method can fuse non-
n
2
sampled data just by
analyzing the possible observation structure to design the observation model of the stacked dynamic system.
Simulation result of three sensors with sampling interval 1, 2 and 3 shows the efficiency of this method.
1 INTRODUCTION
In many fields, such as, automatic control,
aerospace, communication, navigation and
production industry, more than one sensor is used to
gather complete information of the object or process.
According to the mechanism of each sensor, they
can be placed on different scales and the sampling
rate of these sensors may also be different. The
research of multi-sensor data fusion for dynamic
system is significant both in practice and
theoretically (Wen 2002a, Wen 2002b, Lang
Hong1994). Especially, in many cases, the sampling
interval may not equal to
n
2
, thus it is inconvenient
for us to fuse information provided by these sensors.
Therefore the tracking or estimation accuracy may
be strongly reduced.
The main technique used in multi-scale data
fusion is Kalman filter and wavelet analysis. Kalman
filter can result in real-time, recursive and optimal
estimate while it doesn’t take the multi-scale
character of the object into account. Wavelet
transform can implement multi-scale analysis and
estimation of the dynamic system, but the estimate is
neither real time nor recursive (Wen 2002a).
Using Kalman filter, data fusion algorithm for
multi-sensor sampling at same rate has been
successfully developed. Coporating with multi-scale
theory, multi-scale data fusion algorithm for multi-
sensor sampling at
n
2
interval has also been
developed. Limited by the fact that signals to
implement wavelet transform must have the length
of
q
2 , the method mentioned in (Wen 2002b, Lang
Hong1994) can’t solve the data fusion problem
when the sensors used are not sampling at
n
2
interval.
We find that once the dynamic system is stacked
in a given length
q
2
, sensors not sampled at interval
n
2
has different observation structure on each block,
that is, the length of the observation vector on each
block may be different, and the sampling rule on
each observation block is also different.
Based on the hybrid wavelet and Kalman filter
sequential fusion method developed in (Wen 2006a,
Zhou 2007), we are intend to develop a sequential
fusion scheme by designing the stacked observation
model to fuse the observation data coming from
those sensors sampling at non-
n
2
interval.
244
Zhou F. and Tang T. (2008).
HYBRID WAVELET-KALMAN FILTER MULTI-SCALE SEQUENTIAL FUSION METHOD.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 244-248
DOI: 10.5220/0001483702440248
Copyright
c
SciTePress

2 MANUSCRIPT PREPARATION
2.1 Dynamic System
Considering a system involving
K
sensors
)()()()1( kwkxkAkx +=+
(1)
)()()()(
iiiiiii
kvkxkCkz
+
=
Ki ,,2,1 "=
(2)
where
Nk ∈ , kdk
ii
= , Nd
i
∈ is the sampling
interval of each sensor,
n
Rkx ∈)( is the object’s
state,
nn
RkA
×
∈)( is the system matrix.
The System’s process noise
n
Rkw ∈)( is the
Gaussian white noise with the following statistics
0)}({ =kwE (3)
lk
T
kQlwkwE
,
)()}()({
δ
=
0, ≥lk (4)
)(kQ
is a nonnegative matrix.
The observation noise
)(
ii
kv is also Gaussian
white noise
0)}({ =
ii
kvE (5)
lkjij
T
jii
kQlvkvE
,,
)()}()({
δδ
=
Kji ,,2,1, "=
(6)
)0(x is the initial state of the system,
0
)}0({ xxE = (7)
000
}])0(][)0({[ PxxxxE
T
=−− (8)
)0(x , )(kw and )(
ii
kv is independent.
2.2 Stacked System
Rewrite the dynamic model (1) and (2) as a stacked
system with block length
M
)()()()1( mWmXmAmX +=+
(9)
)()()()( mVmXmCmZ
iii
+=
Ki ",2,1=
(10)
where
TTT
MMmxMmxmX )])1((,),1)1(([)( +−+−= "
(11)
])(,,)([diag)(
1
0
1
0
∏∏
−
=
−
=
−+−=
M
j
M
j
jMmMAjmMAmA "
(12)
T
iii
T
i
ii
T
iii
T
ii
mrdmSmMz
mrdmMzmrdmMzmZ
))]()()1((,
))
,
(2)1(()),()1(([)(
−+−
−+−−+−=
"
(13)
where
)(mZ
i
is the observation of m th block
observed by sensor
i .
)(mC
i
in equa.(14) is the
observation matrix,
ii
dMmmr mod)1()( −= ,
)(ae is the unit vector whose a th element is 1,
while other elements are all 0.
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−⋅−+−
−⋅−+−
−⋅−+−
=
))()(())()()1((
))(2())(2)1((
))(())()1((
)(
mrmSemrdmSmMC
mrdemrdmMC
mrdemrdmMC
mC
iiiiii
iiiii
iiiii
i
#
(14)
Section 4.2 shows the detailed designing of
)(mC
i
.
)(mV
i
is the observation noise with statistics
{
}
0),( =smVE
i
(15)
tsjii
T
ji
RtmVsmVE
,,
)},(),({
δδ
=
)(,,2,1, mSts
i
"=
(16)
where
)(mS
i
is the length of the observation vector
on the
m th block.
)(mW
is the process noise
)(
~
)()( mWmBmW =
(17)
TTT
MMmwMmwmW )]12)1((,),1)1(([)(
~
−+−+−= "
(18)
0)]([ =mWE
(19)
0)()(
~
)()]()([)( ≠=≡ mBmQmBmWmWEmQ
TT
(20)
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−+
−+−+
−−
=
∏
∏∏
∏∏
−
=
−
=
−
=
−
=
−
=
IjMmMA
IjmMAjmMA
IjmMAjmMA
mB
M
j
M
j
M
j
M
j
M
j
""
""""
"
""
2
0
2
0
2
0
3
0
2
0
)1(000
00)1()1(0
00)()(
)(
(21)
T
MMmQMmQdiagmQ )]12)1((,),1)1(([)(
~
−+−+−= "
(22)
in equations (14)-(22),
],,,[ ZYXdiag "
is the
blocked diagonal matrix.
2.3 Multiscale Stacked System
Implementing wavelet transform on equation (9)
)()()()1( mWWmXmAWmXW
XXX
+=+
(23)
That is
)()()()1( mmmAm
w
μγγ
+=+ (24)
HYBRID WAVELET-KALMAN FILTER MULTI-SCALE SEQUENTIAL FUSION METHOD
245
where
X
W
is the operator matrix of wavelet transform,
satisfying[Wen 2002 a, Lang Hong1994]
IWW
XX
=
*
)()( mXWm
X
=
γ
(25)
)()( mWWm
X
=
μ
(26)
*
)()(
XXw
WmAWmA =
(27)
*
)()(
XXw
WmQWmQ =
(28)
It is easy to prove that the process noise of the
new stacked system (24) is statistically independent,
that is
0)( =mQ
w
, which is also one of the
advantages of hybrid wavelet-Kalman filter: de-
correlating the correlation between blocks (Wen
2006a).
With the orthogonality of
X
W
, we can rewrite the
observation equation as
)()()()(
*
mVmXWWmCmZ
iXXii
+=
(29)
)()()()(
*
mVmWmCmZ
iXii
+=
γ
Ki ,,2,1 "=
(30)
)()( mXWm
X
=
γ
(31)
That is
)()()()(
*
mVmWmCmZ
iXii
+=
γ
Ki ,,2,1 "=
(32)
3 HYBRID WAVELET-KALMAN
FILTER MULTI-SCALE
ESTIMATION FOR A SINGLE
SENSOR
The following state transition equation and the
observation equation of the wavelet transform
coefficient of the
m
th block can be
established(Tong 2000)
),(),()1,( smwsmsm +=+
γ
γ
,
1,,2,1,0
1
−
= Ss "
(33)
),(),(),(),(
11
smVsmsmHsmZ +=
γ
,
1
,,2,1 Ss "=
(34)
where
),( smZ
is the observation at time s of block
m
. In equa.(34),
T
WmCmH )()( ≡
(35)
where
),( smH
is the s th row of the matrix
)(mH
.
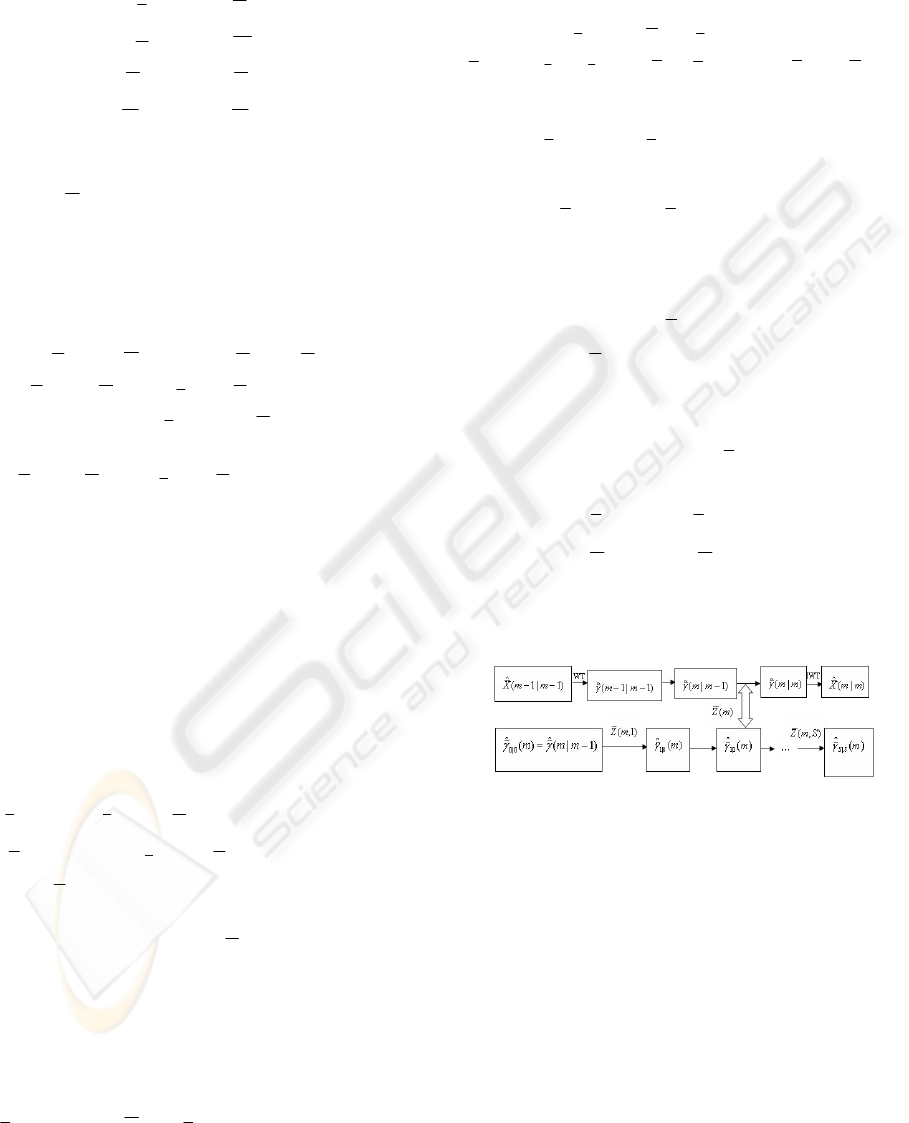
The main idea of hybrid wavelet-Kalman filter
method includes two steps (Wen 2006 a, Wen 2006
b, Zhou 2007):
(1) Wavelet transform coefficients prediction
based on stacked dynamic system
)1|1(
ˆ
)()1|(
ˆ
−−=− mmmAmm
w
γγ
.
(2) Use each observation on this block to update
the estimation of wavelet transform coefficient.
Implement Kalman filter on the system given by
equa. (33) and (34). In each block, the original state
can be derived by a prediction process
)1|1(
ˆ
)()(
ˆ
0|0
−−= mmmAm
w
γγ
(36)
)()()1|1()()](
ˆ
)(
ˆ
[)(
0|00|00|0
mQmAmmPmAmmEmP
w
T
www
T
+−−=≡
γγ
(37)
The filter process follows as
)1,(
~
)1()(
ˆ
)(
ˆ
|11|1
+++=
+++
smZsKmm
ssss
γγ
1,,2,1,0
1
−= Ss "
(38)
)(
ˆ
)(
ˆ
||1
mm
ssss
γγ
=
+
(39)
)()(
||1
mPmP
ssss
=
+
(40)
1
|1|1
)]1,()1,(
)()1,()[1,()()1(
−
++
+++
++=+
smRsmH
mPsmHsmHmPsK
T
ss
T
ss
(41)
)(
ˆ
)1,()1,()1,(
~
|1
msmHsmZsmZ
ss+
+−+=+
γ
(42)
)()]1,()1([)(
|11|1
mPsmHsKImP
ssss +++
+
+
−
=
(43)
This filter process is essentially the gradually
updating of the prediction
)(
ˆ
0|0
m
γ
.The final
updating as the estimation of this block
)(
ˆ
)|(
ˆ
11
|
mmm
SS
γγ
=
(44)
)()|(
11
|
mPmmP
SSw
=
(45)
The whole process of hybrid wavelet-Kalman
filter method can be shown in figure 1.
Figure 1: Hybrid wavelet-Kaman filter Algorithm.
4 NON-
n
2
SAMPLED DATA’S
SEQUENTIAL FUSION
4.1 Sequential Fusion based on Hybrid
Wavelet-Kalman Filter
To fuse the observation data coming from multiple
sensors we can simply cascade these data
sequentially. Then use the cascaded data to update
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
246
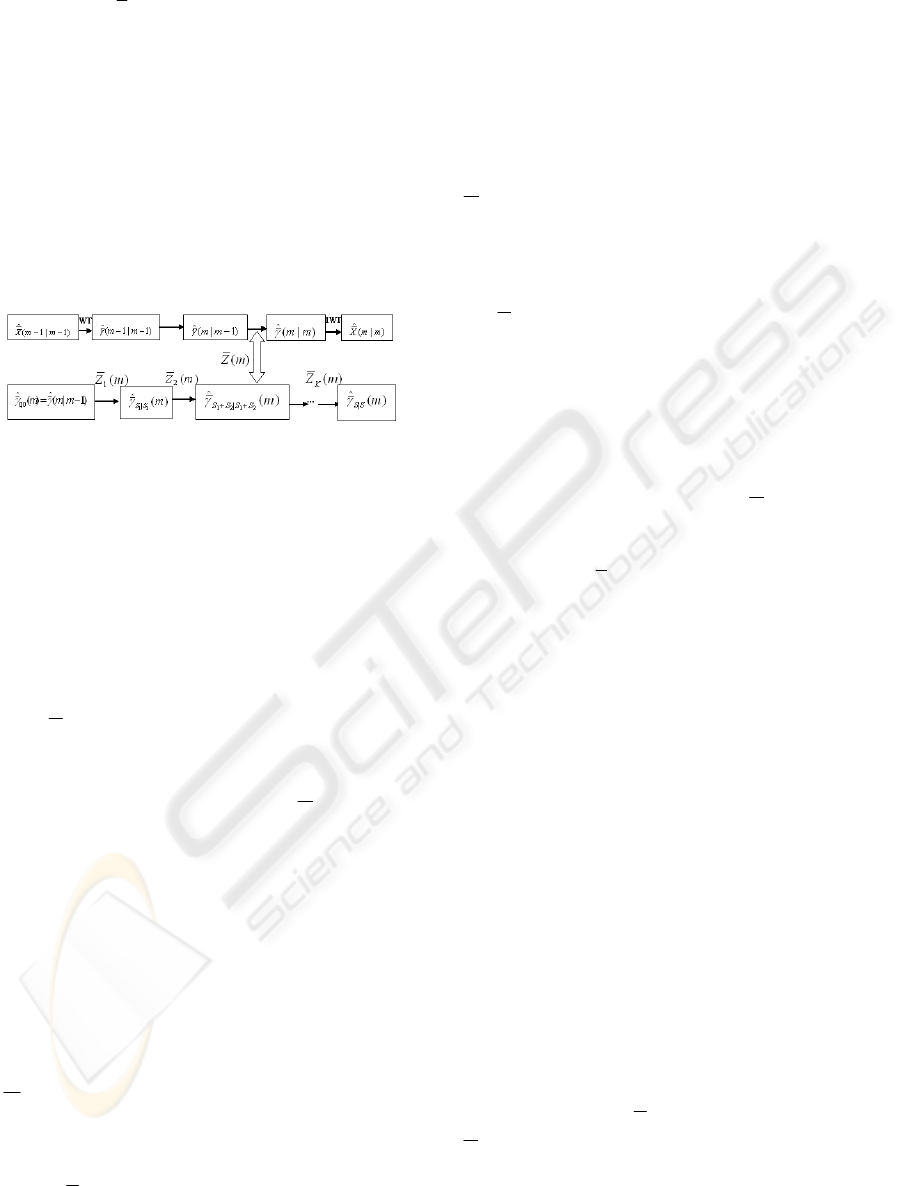
the prediction
)(
ˆ
0|0
m
γ
more times than only one
sensor case. The total updating times is
∑
=
=
K
i
i
SS
1
(46)
This
S
times updating is the fusion estimation of
the wavelet transform coefficient. The sequential
fusion process can be shown in fig.2.
The main advantage of this sequential fusion is
that the fusion estimate process uses the same
mechanism with that of the hybrid wavelet-Kalman
filter in one single sensor case without designing a
new complex fusion rule.
Figure 2: Hybrid wavelet-Kalman filter Sequential fusion.
This sequential fusion algorithm doesn’t require
that the sampling interval of the observation is
n
2
.Thus we can manage to process the fusion
problem involving non-
n
2
sampling data
4.2 Blocked Observation Model for
Non-
n
2 Sampling Case
One crucial step in hybrid wavelet-Kalman filter is
to determine the structure of the stacked observation
matrix
)(mC
i
especially for the non-
n
2
sampling
case since the observation structure and observation
vector of each block are different.
By analyzing, we find that
)(mC
i
varies
periodically with
m
.The varying rule is determined
by the sampling interval
i
d and the block length
M
. The varying period is the minimum common
multiple of
M
and
i
d .
For clarity, we display the observation structure
in the case
4=
M
and
3
=
i
d
,
8=M
and 3
=
i
d
for the system
1=n ,
AkA =)(
,
iii
CkC =)(
.
For
4=
M
and 3=
i
d , the period of
)(mC
i
is 12, that is 3 blocks. In these 3 blocks,
sensor
i
samples 4 observation data in total.
⎪
⎩
⎪
⎨
⎧
=⋅
−=⋅
−=⋅
=
jmC
jmC
jmC
mC
i
i
i
i
3]1000;0001[
13]0010[
23]0100[
)(
(47)
where semicolon denotes another row in the matrix.
Equation (59) means that in the
23 −= jm
block,
sensor
i sampled 1 observation data; in the
13
−
=
jm
block, sensor
i
sampled 1 observation
data; in the
jm 3
=
block, sensor
i
sampled 2
observation data.
For the case
8
=
M
and 3=
i
d , the period of
)(mC
i
is 24, that is 8 data blocks. In these 8 blocks,
sensor
i samples 8 observation data in total. The
resulted stacked observation matrix is
⎪
⎩
⎪
⎨
⎧
=⋅
−=⋅
−=⋅
=
jmeeeC
jmeeeC
jmeeC
mC
i
i
i
i
3];;[
13];;[
23];[
)(
852
741
63
(48)
in the
23
−
=
jm
block, sensor i sampled 2
observation data; in the
13 −= jm
and
jm 3
=
block sensor
i sampled 3 observation data.
More generally, for
q
M
2=
and
i
d without
Nu
∈
s.t.
u
i
d 2=
, the structure of
)(mC
i
is
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−⋅
−⋅
−⋅
=
))()((
))(2(
))((
)(
mrdmSeC
mrdeC
mrdeC
mC
iiii
iii
iii
i
#
(49)
where
)(mS
i
is the number of matrix rows which
is the maximum integer s.t.
mMmrdmS
iii
≤− )]()([
5 SIMULATION
This section gives the simulation of the algorithm
developed in this paper to demonstrate its validity.
Multiscale sequential fusion result of 3 sensors
whose sampling interval are respectively 1,2 and 3
are compared with that of one single sensor using
Kalman filter method.
The parameters used in the simulation
are
96.0)(
=
kA
,
1)(
=
kQ
, the initial state is
1
0
=
x ,
1
0
=
P
.Stacking the system with block
length
4
=
M
, then use the Haar wavelet to
implement wavelet transform. The observation
parameters are
41
)( ImC =
and
5.0
1
=R
;
]1000;0010[5.0)(
2
⋅=mC
and
1.0
2
=R
;
HYBRID WAVELET-KALMAN FILTER MULTI-SCALE SEQUENTIAL FUSION METHOD
247
⎪
⎩
⎪
⎨
⎧
=⋅
−=⋅
−=⋅
=
jm
jm
jm
mC
3]1000;0001[2
13]0010[2
23]0100[2
)(
3
,
01.0
3
=R
.
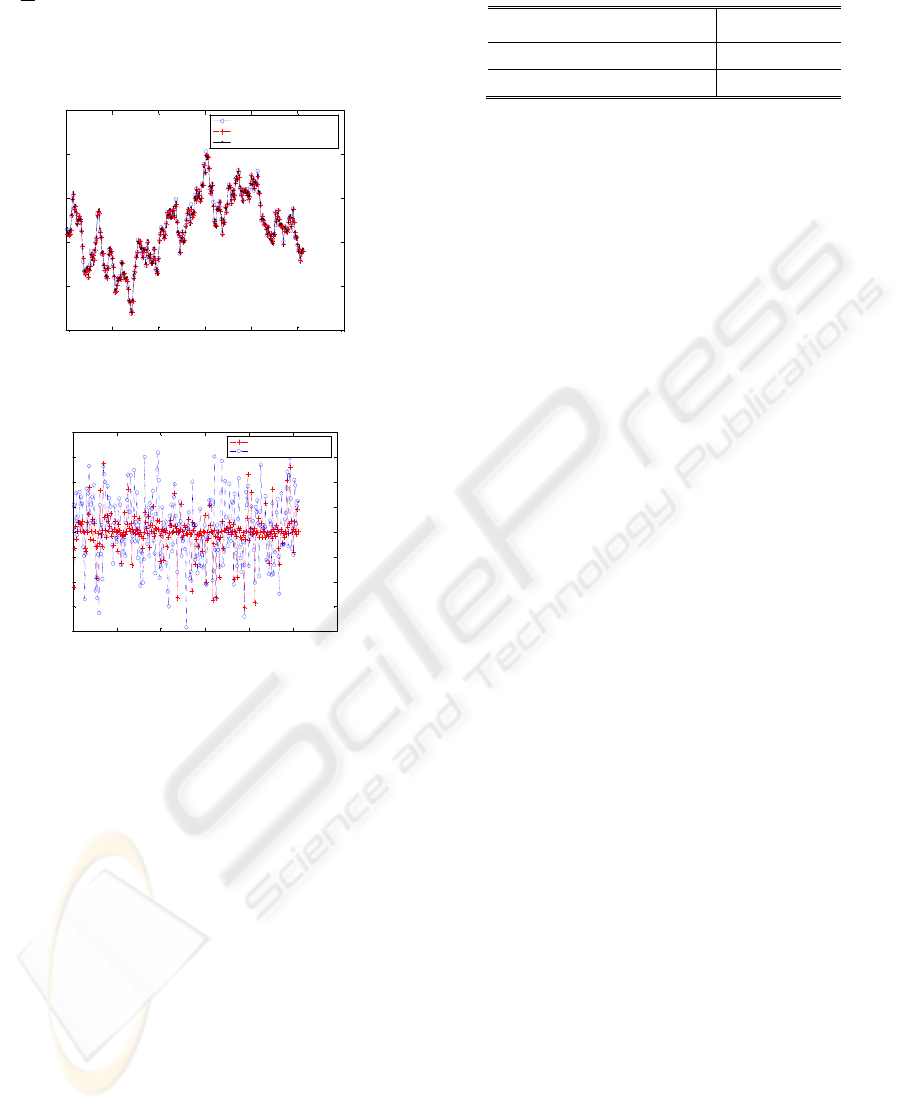
0 50 100 150 200 250 300
-10
-5
0
5
10
15
original signal
sequential fusion estimate of 3 sensors
Kalman estimate of 1 sensor
Figure 3: Sequential fusion result via single sensor
estimate.
0 50 100 150 200 250 300
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
sequent ial fusion estimate error
Kalman estimate error
Figure 4: Sequential fusion error via single sensor estimate
error.
It is easy to see that using the method mentioned
in section 4 to design the stacked observation model
can realize the multiscale sequential fusion of non-
n
2
sampling data. Compare the fusion estimate
using this multiscale sequential fusion method and
one single sensor estimate using Kalman filter,we
conclude that it is an efficient method to process
fusion problem with non-
n
2
sampling observation
data, which is an obstacle of multi-scale data fusion.
The mean of absolute error (MAE) displayed in
table 1 compare the estimate error accuracy based on
one single sensor 1 using Kalman filter method and
that based on sensor multi-sensor using the
multiscale sequential fusion. We find that the
estimation accuracy improved 2.53 times.
Table 1: MAE of sequential fusion and single KF.
6 CONCLUSIONS
Hybrid wavelet-Kalman filter method can obtain the
real time multi-scale estimate of dynamic system.
The multiscale sequential fusion algorithm based on
it can easily fuse information from multiple sensors
sequentially without designing other complex fusion
algorithm. In addition, the hybrid wavelet-Kalman
filter multiscale sequential fusion method can used
to fuse non-
n
2
sampled data just by designing the
periodically varied stacked observation matrix.
ACKNOWLEDGEMENTS
This paper is supported by NSFC (60434020,
60572051); the Education Key Project (07ZZ102)
and the Education Development Project (08YZ109)
from Shanghai Municipal Education Commission.
REFERENCES
Wen Chenglin, Zhou Donghua, 2002. Multi-scale estimate
theory and application, Being jing: Qstinghua
Publication House.
Wen Chenglin, Jin Feng, Zhou Donghua, 2002. Multi-
scale estimate algorithm for one single sensor and one
model, Journal of Electronics 30(6):819-822.
Lang Hong, 1994. Multi-resolution distributed filtering.
IEEE Transactions on AC, 39(4): 853-856.
Tong Xinzheng, A.A.Girgis, E.B.Makram, 2000. Hybrid
wavelet-Kalman filter method for load for forecasting.
Electric power systems research. 54(2):11-17.
Wen Chenglin, Xie Jin, Zhou Funa, Wen Chuanbo, 2006.
A New Hybrid Wavelet-Kalman Filter Method for the
Estimation of Dynamic System .Journal of
Electronics(China),23(1):139-143.
Chenglin Wen, Chuanbo Wen, 2006. The Multiscale
Sequential Filter with Multisensor Data Fusion.
Proceedings of the 25th Chinese control
conference:483-488. Harbin, Heilongjian, China.
Funa Zhou, Tianhao Tang, Chenglin Wen, 2007. A New
Multiscale Estimation Scheme for Dynamic System.
Proceedings of the 26th Chinese control
conference(5):396-400. Zhangjiajie, Hunan, China.
MAE
single sensor Kalman filter 0.2169
3 sensor sequential fusion 0.0857
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
248
