AN APPROACH FOR A KNOWLEDGE-BASED

NC PROGRAMMING SYSTEM

Ulrich Berger, Ralf Kretzschmann and Jan Noack

Brandenburg University of Technology, Siemens-Halske-Ring 14, Cottbus, Germany

Keywords: NC-programming, Graph theory, Process planning, Planning and Scheduling, Knowledge management.

Abstract: Nowadays, significant deficiencies exist in the information flow and access along the NC (Numerical

Control) process chain. These deficiencies are solved insufficiently by introducing CAD/CAM systems and

feature-oriented specification languages. In contrast the application of new production and new machining

systems requires an intensive information exchange. The introduced approach enables the preparation for

feature-based work plans with methods known from the graph theory as a knowledge-based NC

programming system. Therefore the work plan will be mapped into a directed graph in a mathematically

defined way. Based on that, it is possible to use algorithms to find the shortest path and a Hamiltonian path

inside this directed graph under given requirements. Thus, the work plan will be structured and re-ordered.

Finally the corresponding NC paths will be generated and distributed to the machinery. Thence in this in-

process paper the requirements, the investigation and the selection of suitable knowledge structuring

concepts, mathematically basics and the work flow in such a system will be pointed out. Finally a

preliminary prototype will be introduced.

1 INTRODUCTION

The current situation for mould and die makers is

characterized by increasing requirements from the

customer side on quality and individualization of

products (e.g. tools) and also uprising pressure on

product prices at the same time. Furthermore, new

manufacturing technologies like the hybrid

combination of milling with dry iced blasting and

laser ablation for high precision finishing are already

introduced and established. Thus, the NC process

chain is getting more complex. Additionally more

information has to be handled and exchanged

between the different phases of the process change.

However, the effective programming of NC

programs is still a bottle-neck within this process

chain. The reason is the mangled information

exchange caused by prevalent organizational and

technical obstacles like the use of the DIN 66025 /

ISO 6983 as NC programming interface (DIN

66025, 1983). A solution to optimize NC

programming will be enabled by introducing feature

technology. With the help of knowledge-based

machining feature as the elemental part of a NC

program the selection and re-ordering of these

elements can be executed in a mathematical defined

way. With the help of mathematical defined

mappings, it is possible to transfer a work plan of a

NC program in a directed graph (Hamelmann, 1995)

for further processing. As a consequence, the well-

known algorithm from the graph theory and

combinatorics can be used to process and optimize

the graphs under given requirements as objective

functions e.g. time reduction, in a traceable way. As

a consequence present requirements from the

industry (e.g. more transparency and reducing the

processing time) can be achieved.

The following article presents an approach for

structuring and re-ordering NC programs in a

knowledge-based NC programming system based on

feature technology and the application of algorithms

known from the graph theory.

2 STATE OF THE ART AND

RELATED WORK

2.1 NC-Process Chain

The NC process chain consists of three fundamental

steps. First of all, the part (workpiece) including

manufacturing requirements has to be designed with

120

Berger U., Kretzschmann R. and Noack J. (2008).

AN APPROACH FOR A KNOWLEDGE-BASED NC PROGRAMMING SYSTEM.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 120-126

DOI: 10.5220/0001483901200126

 SciTePress

powerful CAD (Computer Aided Design) software

systems.

Afterwards, the following planning phase

consists of further detailed sub process-steps. The

main step is the preparation of the work plan which

will be used for the NC programming in order to

compile the instructions for the NC machining.

Thus, a work plan summarizes all information about

the machining task including the raw part geometry,

the workshop equipment and the sequence of the

machining operations. The complexity of the

workpiece and the generated work plan determines

the used NC programming method. The common

used methods are shop-floor-oriented programming

procedure (SOP) and powerful CAP (Computer

Aided Planning) and/or CAM (Computer Aided

Manufacturing) software applications in order to

generate the DIN 66025 / ISO 6983 based NC code

instruction (DIN 66025, 1983).

Finally, the part will be machined by NC

machines executing these generated instructions in

the shop-floor as the last step in the process chain

(Eversheim, 1996). The NC programs have to be

distributed to the dedicated machinery at the right

time according to the production, planning, and

scheduling results by a DNC (Distributed Numerical

Control) system. These shop-floor scheduling tasks

are supported by MES (Manufacturing Execution

System) based on models like MRP II

(Manufacturing Resources Planning). Determining

factors for the shop-floor scheduling are the

machinery, the tools, the operators and constraints

regarding to the capacity and time scheduling

(Eversheim, 1996).

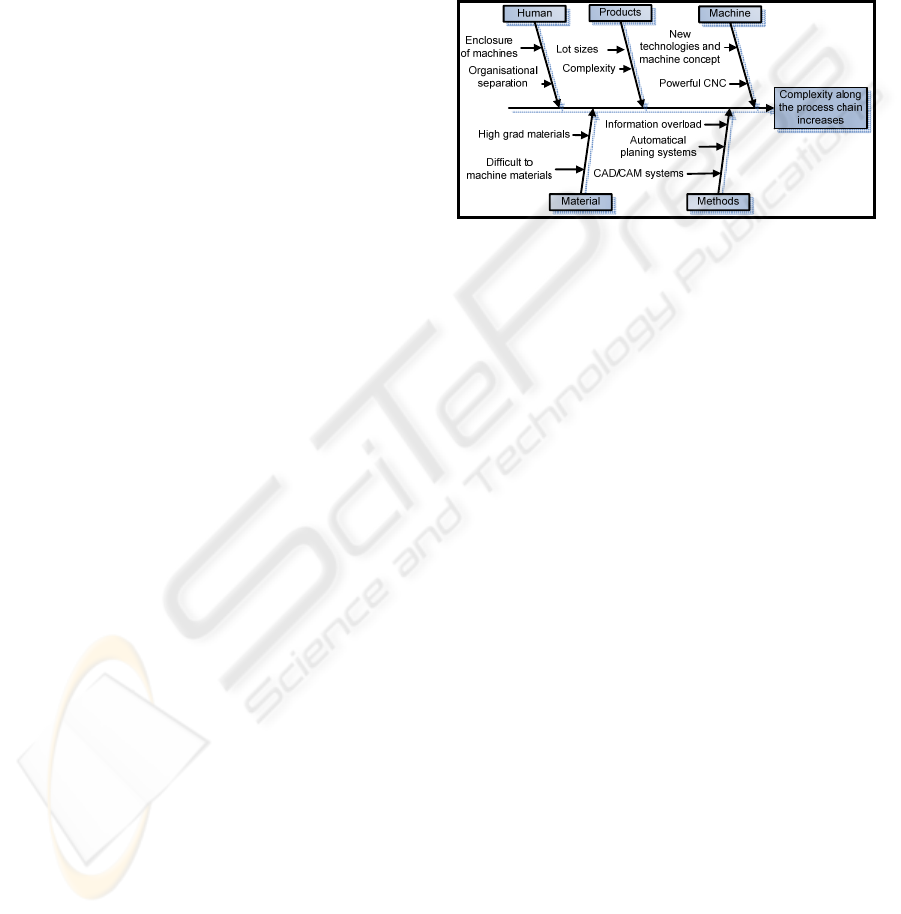
2.3 Problems and Challenges

As already mentioned the NC machining process is

characterized by permanent enhancements. There

are five factors, which influence these enhancement

and complexity of the process chain as seen in

Figure 1. The first and the second factors are dealing

with the manufacturing of complex products with

variable lot sizes, the machining of new resources

e.g. expensive materials which are difficult to

machine like nickel for turbine blades. The

consequence is that complex programs have to be

generated. So, more potential programming errors

has to be avoided in the CAM system. But these

systems do not consider all information concerning

the machinery. The result is that the programs are

not 100% verified (Warnecke, Valous, 1993). The

third part deals with the operator on the machine and

the programmer in the process planning phase. The

fourth factor is the use of multi-axis-machining and

hybrid technologies like machining with dry ice

blasting and laser ablation. Therefore the NC

process chain comprehends knowledge intensive

processes. A new knowledge exchange is enabled

within these phases with the help of new methods

(fifth factor) like the use of integrated design and

process planning by joining CAD and CAM systems

and introducing the feature technology paradigm.

Figure 1: Complexity along the NC process chain.

Several solution approaches are presented in last

years in order to reduce the disadvantages of the

DIN 66025. The most promising project STEP-NC

as a high level and feature oriented programming

language demonstrated very good laboratory result

(Weck et al., 2001). The main idea was to provide

the CNC controller more structural information

about the machining process as the DIN 66025 does.

Thus, several research projects using STEP-NC were

very promising (Pritschow, Heusinger, 2005).

Apparently STEP-NC has been aborted because of

the complexities in its practical implementation.

Further approaches retaining the DIN 66025 were

introduced by Gerken (Gerken, 2000) and by

Hamelmann (Hamelmann 1996). The concepts of

Gerken used Case-based-Reasoning (CBR) for

finding a suitable machining operation for a given

unknown machining task by comparing already

machined tasks with the selected operation. In

contrast to that Hamelmann used rules-based

structures to store the process planning and

operating knowledge in order to reuse it.

Nevertheless, the information and knowledge

exchange from and to the shop floor is still

handicapped by using the DIN 66025 exclusively for

generating NC programs for a fixed setup. Thus, the

short-term shop-floor scheduling is prevented. As a

consequence, it is hard to modify these NC

programs, if the allocation will change because of

unpredictable states in the machinery. An

information feedback of these modified NC

programs fails because of missing or insufficient

AN APPROACH FOR A KNOWLEDGE-BASED NC PROGRAMMING SYSTEM

121

information feedback possibilities back to the design

and process planning. As the result, the knowledge

is kept on the one hand in the design and process

planning phase and on the other hand in the shop-

floor. Due to the missing link to the CAM

information, recurrent problems occur (like broken

die and collision), while setting up a machine in the

shop-floor with a new program (Warnecke, Valous,

1993). New solutions are needed.

3 REQUIREMENTS FOR A

KNOWLEDGE-BASED

NC PROGRAMMING SYSTEM

Generally, an approach for such a system has to

structure and re-order the programs in a traceable

and customized way. Regarding to the actual

machinery and production state it must be possible

to change parts of the NC program (operation

scheduling) and the assignments of the machine in

the machinery. The fundamental basis will be the

use of process knowledge provided by the

employees involved in the NC process chain and

process monitoring. As a result, the feature

technology along the whole NC process chain will

be utilized. These features have to be used to

describe the physical design of the workpiece (CAD

model) and the assigned best-practice machining

operations to machine the workpiece (Hamelmann,

1995). Finally, the concrete order of the machining

features will be translated into the DIN 66025

instructions. A feedback from the shop-floor must be

established to guarantee and validate an optimal

assignment of machining operation to design

features. An essential aspect is to enable the

feedback of the operators back to the process

planning about unsuccessful machining operations.

Summarizing, the following requirements have to be

maintained (Berger et al, 2007):

 Feature-based description of the process

planning to benchmark machine operations,

 Knowledge-based algorithms for structuring

and re-ordering the work plan,

 Establishing different user profiles with access

authorization to planning documents,

 DIN 66025 as NC programming language,

 “Add-on” to the prevailing IT architecture,

 Modular architecture for roll out of STEP-NC

4 DEVELOPMENT OF A

KNOWLEDGE-BASED

NC-PROGRAMMING SYSTEM

The development can be divided in four main steps.

At first suitable mathematical descriptions for

defining a work plan have to be investigated.

Secondly, the process planning has to be defined.

Thirdly, the workflow of the system has to be

described. Thirdly, the NC programming system has

to be established as an “Add-on” with access to

several databases according to user profiles and the

prevailing IT architecture.

4.1 Investigating the Mathematical

Description for a Work Plan

Feature-based concepts have been established

already in order to define a work plan (Gerken,

2000) (Weck et al., 2001) (VDI 2218, 2003). The

process of machining a job can be subdivided

hierarchically in several process plan elements

(Gerken, 2000). So, the machining task (as

machining feature) of drilling a step drilling can be

divided in machining operations and machining

steps. Berger and Cai defined a machining step

(MStep) as a product of selected tools (Tool),

technology (Tech), paths and machining features

(MFeat) in order to describe the elements in a

mathematical way (Berger et al., 2005). Thus, a

machining step has to be expanded with the element

machine (Mach). Finally, a set of machining steps

can be defined as a set of 5-tuple (1).

MStepSU

MFeatMachPathTechToolMStep

∈

××

}{

(1)

Each specific 5-tuple set-up (SU) describes the

parameter of a machining process. Consequently,

each machining operation is an assembly of

machining steps. Furthermore, each work plan

consists of a sequence of concrete set-up from

MStep to machine the machining task. Unlike the

STEP-NC data model machining operation, the

MSTEP is defined in a more abstracted way.

4.2 Investigation and Selection of the

Mathematical Model for Processing

a Work Plan Processing

For processing the information of a work plan a

suitable concept which supports the operations of re-

ordering and structuring has to be found. Therefore

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

122

requirements have to be determined and suitable

available concepts have to be benchmarked with

these requirements. As already mentioned the

knowledge-based NC programming system uses

benchmarked features like MStep for structuring the

work plan. Alternative work plan are usable to

machine the same tasks. Therefore the requirements

for a concept are handling time dependency,

outlining different alternatives in a work plan and

benchmarking operations (e.g. association of

MStep). Furthermore, the application of traceable

and well known algorithms for selecting / structuring

and re-ordering alternative operation is required.

Suitable and investigated knowledge representation

and knowledge processing concepts known from the

Artificial Intelligence (AI) are neural networks,

formal rules-based languages and finally methods

based on the graph theory (Görz, 2003). Neural

networks are a set of “neurons”, which are organized

in the input layer, processing layer and output layer.

Neural networks are trained with special training

algorithms. The disadvantage of this “black box”

concept is that the neural networks follow

processing in non traceable way (Görz, 2003).

Therefore, the neural networks do not conform the

requirements. Formal and rule-based languages are

used to formalize a given well structured domain

under discussion (Görz, 2003). Because of missing

algorithms for processing structures like work plans

this concept is not suited, too. The graph theory as

last concept fulfils the given requirements. It is

possible to model time dependency. Furthermore,

the different paths will be utilized to represent the

alternatives within the directed graph. By

introducing “costs” for passing paths the

benchmarking will be enabled. Finally the use of

algorithms introduced in the graph theory like

Floyd-Warshall (FW) algorithm and the TSP

(Travailing Salesman Problem) algorithm enable the

processing of the work plan. The methods from the

combinatorics are used to transfer the task of

generating an optimized work plan as operations

research problem. Thus, a complete work plan

consisting of a sequence of elements of MStep can

be transferred in a directed graph. A directed graph

DG is defined as an arrangement of a set of nodes

(edges) V and a set of edges or arcs E. These arcs

are connecting two nodes out of the set of nodes

(Jungnickel, 1990). Regarding the work plan, the set

of separate MStep can be transferred in the set of

nodes. The arcs between the nodes will represent the

ordering of these two MStep. An arc e = (a,b)

means, that the MStep a is ahead of MStep b.

Therefore time dependency of different elements

from MStep can be modeled. At this moment, an arc

has no quantifier and emblematizes a connection

between two MStep. By introducing a quantifier, the

arcs become an additional dimension “cost”. This

cost is an assembly of two efforts to pass this arc.

The first effort is the cost to apply the first

machining step a. The second effort represents the

cost to pass to the second step b. It is possible to

enhance the second cost by adding additional cost as

a sum of all costs, which occur by passing to all

other nodes in graph. Thus, a target system of

different criteria like machining time, machining

quality, and machining energy can be defined to

calculate the costs. Therefore a need of additional

information concerning the machinery is detected.

Now, it is possible to change the value of a

quantifier corresponding to a given scenario, which

will be described by a concrete specification of these

criteria. Summarizing a work plan consisting of

MStep can be described as a directed graph with

edges and arcs in-between the edges. Now, it is

possible to use algorithms known from the graph

theory to calculate significant paths through the

directed graph. Two major algorithms can be

identified which are suitable for the application in

the field of NC machining (Jungnickel, 1990). At

first, the Floyd-Warshall algorithm calculates the

shortest distance (as a total sum of arc quantifiers)

between two nodes (machining step) with the help of

the transitive closure. With the help of this algorithm

different alternatives for the same machine feature

can be rated. The complexity is O(n³), where n is the

amount of nodes. Secondly, the TSP solving

algorithms can be executed in order to re-order all

machining steps in a work plan to get lowest cost in

total to machine all MStep in a row (as Hamiltonian

path). The TSP is NP-complete. Consequently, the

optimal path could be calculated by combining all

MStep. But, this algorithm is not an acceptable way

for a common number of MStep. There are several

algorithms to find a heuristic solution for a

Hamiltonian path in acceptable effort. The use of

these heuristic algorithms shortens the runtime of the

combinatoric algorithm (Jungnickel, 1990).

4.3 Workflow for the

Knowledge-Based NC

Programming System

After defining the mathematical background the

workflow for the system has to be specified.

Therefore, the architecture of the system is outlined

in Figure 2.

AN APPROACH FOR A KNOWLEDGE-BASED NC PROGRAMMING SYSTEM

123

Figure 2: Architecture of the approach.

The knowledge-based NC programming system will

be used as a process planning tool. The tool has

access to the knowledge-base (KB) and to the CAD

and CAM systems. The workflow is divided into

three operations (I-III).

Figure 3: Workflow of the approach.

In Figure 3, the workflow of the approach is

presented. The initial task is to generate a work plan

for machining a work piece. Therefore, a design

feature-based CAD model will be investigated. At

first, the sequence of the design feature will be

determined (manually or with help of permutation).

Afterwards, each design feature will be transferred

into suitable alternative machining features which

are stored as an assembly of MStep in the KB. Thus,

a work plan can described as a sequence of MStep as

mentioned before. In Figure 4(a), a specimen work

plan is given with three design features, which can

be mapped into six machining features (MF). Each

of the machining features will be represented by

machining steps. The machining features MF1a and

MF1b have a shared machining step MStep1 (e.g.

roughing) and two alternative steps MStep2a

(finishing 3-axis) and MStep2b (finishing 5-axis).

The machining feature MF2 will be represented by

one machining step. Finally the last design feature

can be represented by three machining feature

(MF3a … MF3b) with three alternative machining

steps (MStep5a … MStep5c). To solve the

alternatives, limitations for the machining steps will

be given by using scenarios as mentioned before. A

scenario describes a special combination of criteria

to calculate a quantifier for each element from

MStep and each arc. The process planning tool

defines a machining scenario from the given

scenarios profiles. The selected scenario defines

ranges for each criterion. Possible criteria are

machining time, tool change count, and surface

quality. Afterwards, the process planer will select

the right alternative with the Floyd-Warshall (or

variation), which calculates the “shortest path”

between the additionally added start node “S” and

end node “E”. A suitable work plan as result is

structured and bold marked in Figure 4a.

Figure 4: Specimen work plan (a) and directed graph (b)

with Hamiltonian path (without quantifiers).

The following task is re-ordering the work plan in

order to find a sequence of the MStep with the least

sum of quantifiers between the MStep in total. The

Hamiltonian path can describe such a path.

Therefore the graph has to be enriched with

additions of arcs, which represents additional

dependencies as seen in Figure 4b. Afterwards

calculation criteria will be set, before calculating the

Hamiltonian path. These criteria specify the

quantifier a second time. Possible quantifiers are the

same machine, same clamping, same tool and same

type of operation. Finally a suitable Hamiltonian

path can be calculated. The grade of the path is

depending on the executed algorithm. The best path

can be archived by the combination of all

possibilities (Brute-Force algorithm). This algorithm

is NP-complete. The uses of heuristic algorithms

shorten the runtime drastically. But is it not

guaranteed, that they will find the best path through

the work plan. A possible Hamiltonian path through

the example is shown in Figure 4b. Finally a CAM

model generates the NC program corresponding to

the given re-ordered work plan by translating the

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

124

machining steps. The optimized NC program is

found. Finally the scheduled NC programs will be

dispatched to the corresponding machine. The

operator has now the possibility to benchmark the

machining steps for re-using them.

4.4 Integration in the NC - Process

Chain

The knowledge-based programming system has to

be embedded in a guidance system. Therefore it will

be structured into two major parts, which are

integrated in already existing applications. At first

the approach will be integrated in the machines on

the shop floor. So the user can access additional

planning information with the help of an information

system as front-end of the guidance system.

Secondly a module called “process planning tool”

will be integrated in the guidance system and

supports the knowledge-based process planning with

the already introduced methodology and functions.

5 TECHNICAL REALIZATION

The technical realization of the concept for the

knowledge-based NC programming will be

implemented in two steps. At first, the proposed

process planning tool will be implemented.

Therefore Visual Basic (VB) is used as

programming language with access to MS Visio as

visualization tool and MS Access as knowledge

base. Corresponding to the figure 2, the first (I

Sequencing) and the second (II Structuring) part of

the architecture are already implemented. The

structure of the prototype is outlined in Figure 5. At

first the sequenced work plan will be transferred into

a VB program and visualized with MS Visio.

Afterwards, the FW implementation calculated the

optimal structure of the work with the help of

additional information about tools, machinery

provide by the knowledge base. The next step will

be to work on the interface specifications and the

investigation of the use of the algorithm for the TSP

algorithm. The gist will be the decrease of runtime

of this NP-complete algorithm. Thus, several

algorithms are investigated which that follow

heuristic approaches.

Figure 5: Prototype of the application.

As seen in figure 6 “Brute-Force” algorithms have a

high exponential running time. In contrast to that,

the heuristic algorithm “All nearest neighbor”

(ANN) and the “Minimum spanning tree” has lower

running times. The ANN as simple heuristics will be

used to carry out the implementation in the way that

exclusively time independent MStep will be selected

as lowest distance MStep in the ANN algorithm.

100

10000

100000

1E+08

1E+10

1E+12

1E+14

12345678910111213141516

MStep

Running Time

Brute-Force ANN Minimum spanning tree

Figure 6: Running time of different TSP algorithms.

Finally, the approach will be realized as an

information system as a client-server-application.

The mobile client suits industrial need. The server

provides in addition an interface to the CAM system

CATIA V5. A 5-axis machining centre will be

completed the experimental setup. In this current

development status of the information system the

user has access to the product data of the CAD

module and planning data of the CAM module. Thus

the first feedback from the shop floor will be

enabled. The user can directly modify parameters of

the process planning of turning and milling tasks in

the actual implementation status.

AN APPROACH FOR A KNOWLEDGE-BASED NC PROGRAMMING SYSTEM

125

6 CONCLUSIONS AND

OUTLOOK

Nowadays, there are significant deficiencies in the

information flow along the NC process chain. The

reasons are the used insufficient interfaces within the

process chain. Consequently, knowledge is kept in

the uncoupled process chain. The deficits could be

solved insufficiently with the help of common

integrated CAD/CAM software solutions.

Modifications in the shop-floor and the handling of

alternative machining strategies are not supported in

an adequate way. The presented approach for

knowledge-based NC program is an enabler to

optimize the machining of different tasks under

given scenario. The fundamental concept will be the

use of feature-based designing and process planning.

Therefore, a mathematical description of machining

will be introduced. This specification describes a

work plan as a sequence of machining features with

alternative machining steps. These MStep are

benchmarked with the help of different certain

criteria. The process planer has now the possibility

to select different alternatives parameters for

machining different areas of a workpiece regarding a

given machining scenario. Furthermore a work plan

structuring and re-ordering approach will support the

process planer. For processing a work plan, different

mathematical descriptions were investigated and

assessed. Finally, the MStep-based work plan will be

transferred in a directed graph with nodes as MStep

and arcs as quantified dependences within them. The

application of the Floyd-Warshall algorithm

calculates now the best choice of alternative MStep

for each machining feature. Furthermore heuristics

algorithms for the TSP calculate the optimal

sequence of the received MStep in a work plan.

Afterwards, the optimal work plan will be

transferred to the NC path generator of the CAM

system. A first prototype is implemented step by

step. First results validate the approach. The next

steps will be the enhancement of the prototype in

order to add additional databases to store the MStep

and the structured machinery. Furthermore, the user

profiles have to be defined and implemented

instantly. An algorithm has to be defined, which

suggests possible set-ups for given structured

machining tasks with methods known from the AI

(e.g. CBR). The heuristic TSP algorithm has to be

implemented. Therefore the ANN will be modified

and adapted to the NC process planning. In

conclusion the approach supports the process

planner to select the suitable process operations

corresponding to a given scenario definition.

ACKNOWLEDGEMENTS

The work reported in this paper was partially

supported by EC / FP6 Program, “Development of a

Hybrid Machine Tool Concept for Manufacturing of

Free-form Surface Moulds” (FP6-2004-NMP-NI-4-

026621-2).

REFERENCES

Berger, U., Cai, J., Weyrich, M., 2005. Ontological

Machining Process Data Modelling for Powertrain

Production in Extended Enterprise. Journal of

Advanced Manufacturing System (JAMS), Vol. 4, No.

1 (2005), pp. 69-82.

Berger, U., Kretzschmann, R., Aner, M., 2007.

Development of a holistic guidance system for the NC

process chain for benchmarking machining operations.

In: Proceedings of the 12th IEEE Conference on

Emerging Technologies and Factory Automation,

Greece, September 25-28, 2007.

DIN 66025, 1983. Programmaufbau für numerisch

gesteuerte Arbeitsmaschinen.

Eversheim W., 1996. Organisation in der

Produktionstechnik - Band 1 Grundlagen, VDI-

Verlag, Düsseldorf.

Gerken H., 2000. Management von Erfahrungen mit einem

Assistenzsystem für die Arbeitsplanung, TU-Berlin.

Görz, G., 2003. Handbuch der Künstlichen

Intelligenz, Oldenbourg, München.

Hamelmann, S., 1995. Systementwicklung zur

Automatisierung der Arbeitsplanung, VDI-Verlag

Aachen.

Jungnickel, D., 1990. Graphen, Netzwerke und

Algorithmen, Wissenschaftsverlag, Mannheim.

Pritschow G., Heusinger S., 2005, STEP-NC-basierter

Korrekturkreis für die Schlichtbearbeitung von

Freiformflächen, Jost-Jetter Verlag, Heimsheim.

VDI Richtlinie - VDI 2218, 2003. Informations-

verarbeitung in der Produktentwicklung – Feature-

Technologie.

Warnecke G., Valous A., 1993. Informationsrückkopplung

zwischen NC-Fertigung und Arbeitsplanung,

Schnelldruck Ernst Grässer, Karlsruhe.

Weck M., Wolf J., Kiritsis J, D., 2001. STEP-NC – The

STEP compliant NC Programming Interface, IMS

Forum, Ascona Schweiz.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

126