
LIGHT-WEIGHT REINFORCEMENT LEARNING WITH
FUNCTION APPROXIMATION FOR REAL-LIFE CONTROL TASKS
Kary Främling
Helsinki University of Technology, PL 5500, FI-02015, Finland
Keywords:
Reinforcement learning, function approximation, normalised radial basis function network, eligibility trace,
mountain-car, cart-pole, pendulum.
Abstract:
Despite the impressive achievements of reinforcement learning (RL) in playing Backgammon already in the
beginning of the 90’s, relatively few successful real-world applications of RL have been reported since then.
This could be due to the tendency of RL research to focus on discrete Markov Decision Processes that make
it difficult to handle tasks with continuous-valued features. Another reason could be a tendency to develop
continuously more complex mathematical RL models that are difficult to implement and operate. Both of these
issues are addressed in this paper by using the gradient-descent Sarsa(λ) method together with a Normalised
Radial Basis Function neural net. The experimental results on three typical benchmark control tasks show that
these methods outperform most previously reported results on these tasks, while remaining computationally
feasible to implement even as embedded software. Therefore the presented results can serve as a reference
both regarding learning performance and computational applicability of RL for real-life applications.
1 INTRODUCTION
A Reinforcement Learning (RL) agent can sense the
state of itself and its environment, take actions that
may change that state in some way and improve its
behaviour based on a reward signal that expresses if
one or several actions (or their result) was good or
bad and to what extent. RL is therefore similar to the
way that most animals learn to handle new or chang-
ing situations, e.g. babies learning how to walk and
grab things, children learning how to ride a bicycle
or adults learning how to drive a car. Despite this
relationship with human and animal learning in the
real world, it is surprising how few successful uses of
RL for real-world control applications have been re-
ported. The most well-known success of RL so far
might be the TD-Gammon system (Tesauro, 1995)
that learned to play Backgammon on world-champion
level. However, Backgammon is not a control task
and the methods and results are not easy to extrapolate
to control tasks. A recent success on a real-world RL
control task is the helicopter flight control reported in
(Abbeel et al., 2007). What is common to both of
these successful applications of RL (especially in he-
licopter flight) is that they are the result of rather com-
plex calculations that involve several different learn-
ing phases and extensive hand-tuning by human de-
signers. Even in experiments with standard control
tasks such as those used in this paper, the RL meth-
ods employed tend to be complex and require exten-
sive hand-tuning by human designers in order to make
the learning task feasible. This complexity makes it
difficult to re-use successful RL models in new appli-
cation areas. Such models also tend to be too complex
to provide plausible models of animal learning.
Both TD-Gammon and the helicopter controller
use function approximation in order to be able to
handle the huge state spaces involved. Especially
continuous-valued control tasks tend to be problem-
atic for RL because of their infinite state space. Many
popular RL methods assume that the task to learn can
be represented as a Markov Decision Process (MDP).
In tasks with continuous-valued inputs it becomes
necessary to discretize the state space in order to han-
dle it as an MDP but the discretisation easily leads
to an explosion of the state space. This contradic-
127
Främling K. (2008).
LIGHT-WEIGHT REINFORCEMENT LEARNING WITH FUNCTION APPROXIMATION FOR REAL-LIFE CONTROL TASKS.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 127-134
DOI: 10.5220/0001484001270134
Copyright
c
SciTePress

tion between ‘provably converging’ but ‘hard-to-use
in real-life’ MDP-based methods may also be a rea-
son for the lack of reported successful uses of RL in
real-world control tasks.
In this paper we will show how function ap-
proximation and one of the ‘lightest’ RL methods,
i.e. model-free action-value learning with gradient-
descent Sarsa(λ), can be used for successful learning
of three benchmark control tasks. Less hand-tuning is
needed and learning is significantly faster than in pre-
viously reported experiments. These small memory
and computation requirements and the rapid learning
should make it possible to use RL even in embed-
ded systems that could adapt to their environment.
These characteristics also make the learning biologi-
cally plausible. The experimental tasks used are the
Mountain-Car, Swinging up pendulum with limited
torque and Cart-Pole tasks.
After this introduction, section 2 describes the
background and theory of gradient-descent Sarsa(λ),
then section 3 presents the Normalized Radial Basis
Function approximation technique used, followed by
experimental results in section 4 and conclusions.
2 ACTION-VALUE LEARNING
WITH FUNCTION
APPROXIMATION
Action-value learning is needed in control tasks
where no model of the controlled system is available.
In the case of continuous-valued function approxi-
mation, gradient-descent Sarsa(λ) (Sutton and Barto,
1998, p. 211) can be used:
~
θ
t+1
=
~
θ
t
+ α[r
t+1
+ γQ
t
(s
t+1
,a
t+1
) − Q
t
(s
t
,a
t
)]~e
t
,
(1)
where
~
θ
t
is the parameter vector of the function ap-
proximator, r
t+1
is the reward received upon entering
a new state, α is a learning rate, γ is the discount rate
and Q
t
(s
t
,a
t
) and Q
t
(s
t+1
,a
t+1
) are the action-value
estimates for the current and next state, respectively.
In the case of an accumulating trace, the trace ~e
t
is
updated according to:
~e
t
= γλ~e
t−1
+ ∇
~
θ
t
Q
t
(s
t
,a
t
) (2)
with~e
0
=
~
0. ∇
~
θ
t
f
~
θ
t
, for any function f denotes the
vector of partial derivatives (Sutton and Barto, 1998,
p. 197):
∂f
~
θ
t
∂θ
t
(1)
,
∂f
~
θ
t
∂θ
t
(2)
,...,
∂f
~
θ
t
∂θ
t
(n)
T
, (3)
where
~
φ is feature vector that consist of the state vari-
ables of the task (continuous-valued or not). Eligi-
bility traces can speed up learning significantly by
improving temporal credit assignment. They are in-
spired from the behaviour of biological neurons that
reach maximum eligibility for learning a short time
after their activation and were mentioned in the con-
text of Machine Learning at least as early as 1972 and
used for action-value learning at least as early as 1983
(Barto et al., 1983), where the accumulating eligibil-
ity trace for discrete state tasks (MDP) was proposed:
e
t
(s,a) =
γλe
t−1
(s,a) + 1
if
s = s
t
and
a = a
t
;
γλe
t−1
(s,a)
otherwise
(4)
for all s,a. λ is a trace decay parameter. s corresponds
to the feature vector
~
φ in 3 but is restricted to binary
values. Equation 4 is a special case of equation 2
when using binary state representations because then
∇
~
θ
t
Q
t
(s
t
,a
t
) = 1 when s = s
t
and a = a
t
and zero oth-
erwise. In (Singh and Sutton, 1996) it was proposed
to use a replacing eligibility trace instead of the accu-
mulating eligibility trace:
e
t
(s,a) =
1
if
s = s
t
and
a = a
t
;
0
if
s = s
t
and
a 6= a
t
;
γλe
t−1
(s,a)
if
s 6= s
t
(5)
The replacing eligibility trace outperformed the accu-
mulating eligibility trace in the Mountain-Car task as
reported in (Singh and Sutton, 1996). This is the main
reason why replacing traces are considered to perform
better than accumulating traces. In (Främling, 2007b)
a generalisation was proposed for the replacing trace
that makes it possible to use with continuous-valued
function approximation:
~e
t
= max(γλ~e
t−1
,∇
~
θ
t
Q
t
(s
t
,a
t
)) (6)
As for the accumulating trace, equation 5 is identical
to equation 6 in the case of binary features, except
for resetting the trace of unused actions of the current
state to zero in equation 5. Even though the results
in (Främling, 2007b) seem to confirm the advantage
of replacing traces, especially when not resetting the
traces of unused actions, there is still a lack of evi-
dence on whether this is also true for other tasks. The
experiments in this paper are performed using both
kinds of eligibility traces as an attempt to provide in-
creased insight into this issue.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
128

3 NORMALISED RADIAL BASIS
FUNCTION NETWORK
APPLIED TO ACTION-VALUE
LEARNING
When function approximationwith neural nets is used
for learning an action-value function, an eligibility
trace value is associated with every weight of the neu-
ral net (Barto et al., 1983). Then the eligibility trace
value reflects to what extent and how long ago the
neurons connected by the weight have been activated.
The use of function approximation rather than binary
lookup-tables signifies that more than one feature
value φ can be different from zero. This is also the
case with the binary CMAC (Cerebellar Model Artic-
ulation Controller) neural network (Albus, 1975) used
in (Singh and Sutton, 1996). When using CMAC,
there are as many active features as there are over-
lapping layers in the CMAC, which could lead to
excessive weight changes in Equation 1. In order
to avoid this, (Singh and Sutton, 1996) divide every
value e
t
(s,a) by the sum of all feature values in or-
der to avoid learning divergence as a result of exces-
sive weight changes. No justification was given for
this operation in (Singh and Sutton, 1996) but there
seems to be a connection with the well-known Nor-
malised Least Mean Squares (NLMS) method, where
α in Equation 1 is replaced by α
norm
:
α
norm
= α/
∑
~e
t
. (7)
The use of NLMS for RL in a real-world robotics task
has been studied e.g. in (Främling, 2004) and (Främ-
ling, 2005). When using continuous-valued function
approximation, most terms ∇
~
θ
t
Q
t
(s
t
,a
t
) in equation
2 will be different both from zero and one, which is
the main source of incompatibility between the dis-
crete eligibility traces (Equations 4 and 5) and their
continuous-valued counterparts (Equations 2 and 6).
In order to avoid weight divergence in equation 1,
it can be assumed that an NLMS-type normalisation
would be useful also with continuous-valuedfeatures.
Because NLMS does not seem to have been used in
neural nets, another kind of normalisation than NLMS
is used here, i.e. the Normalised Radial Basis Func-
tion network (NRBF).
The continuous feature values are calculated by an
RBF network as:
φ
i
(~s
t
) = exp
−
(~s
t
−~c)
2
r
2
, (8)
where~c is the centroid vector of the RBF neuron and
r
2
is the spread parameter. The action-value estimate
of action a is:
Q
t
(~s
t
,a) =
N
∑
i=1
w
ia
φ
i
/
N
∑
k=1
φ
k
!
, (9)
where w
ia
is the weight between the ‘action’ neuron a
and the RBF neuron i. The division by
∑
N
k=1
φ
k
, where
N is the number of RBF neurons, is the normalisation
step that ensures that the sum of all φ will be exactly
one. Every parameter w
ia
, has its corresponding eli-
gibility trace value. For the accumulating trace, equa-
tion 2 was used in all experiments, while equation 6
was used for the replacing trace. In all experiments,
an affine transformation mapped the actual state val-
ues from the respective value ranges into the range
[0,1] that was used as ~s. This transformation makes
it easier to adjust the spread parameter (r
2
= 0.01 is
used in all experiments).
4 EXPERIMENTS
The Mountain-Car task (Figure 1) was used in (Singh
and Sutton, 1996) and the results presented there
seem to be the main reason why replacing eligibil-
ity traces are considered to perform better than accu-
mulating traces. The second task consists in swing-
ing up a pendulum with limited torque and keep-
ing it in upright position (Figure 4). The pendu-
lum task is surprisingly difficult for ordinary learn-
ing methods such as Sarsa(λ) with binary represen-
tations (lookup-table, CMAC) due to the non-linear
control function required for passing from swing-
up behaviour to balance-keeping behaviour. For the
Cart-Pole task (Figure 7), successful results were re-
ported using actor-critic and lookup-tables already in
(Barto et al., 1983).
For each task, results are first shown by graphs
that allow comparison between results shown here
and those reported in existing literature. A supple-
mentary graph may be used to show the results in
a homogeneous way between the three tasks that al-
lows to evaluate both learning speed and final perfor-
mance after learning, as well as how well the accumu-
lating and the replacing traces perform in each task.
These graphs are also intended to provide a uniform
benchmark framework for future experiments using
the same tasks.
4.1 Mountain-Car
One of the first presentations of this task seems to be
in (Moore, 1991), where a model of the environment
was learned. The task description used here is identi-
cal to the one in (Singh and Sutton, 1996). The task
LIGHT-WEIGHT REINFORCEMENT LEARNING WITH FUNCTION APPROXIMATION FOR REAL-LIFE
CONTROL TASKS
129

Figure 1: Mountain-Car task.
consists in accelerating an under-powered car up a
hill, which is only possible if the car first gains enough
inertia by backing away from the hill. The task has a
continuous-valued state vector ~s
t
= (x
t
,v
t
), i.e. the
position x
t
and the velocity v
t
. At the beginning of
each trial these are initialized randomly, uniformly
from the range x ∈ [−1.2,0.5] and v ∈ [−0.07,0.07].
The altitude is sin(3x). 8×8 RBF neurons were used
with regularly spaced centroids. The agent chooses
from three actions {+1, 0, − 1} corresponding to for-
ward thrust, no thrust and reverse. The physics of the
task are:
v
t+1
=
bound
(v
t
+ 0.001a
t
+ gcos(3x
t
))
x
t+1
= max{x
t
+ v
t+1
,−1.2}
,
where g = 0.0025 is the force of gravity and the bound
operation places the variable within its allowed range.
If x
t+1
is clipped by the max-operator, then v
t+1
is
reset to 0. The terminal state is any position with
x
t+1
> 0.5. The reward function is the cost-to-go
function as in (Singh and Sutton, 1996), i.e. giving -1
reward for every step except when reaching the goal,
where zero reward is given. The weights of the neural
net were set to zero before every new run so the ini-
tial action-value estimates are zero. The discount rate
γ was one.
Figure 2 shows the average number of steps per
episode for the best α values (4.9, 4.3, 4.3, 4.7, 3.9,
3.3 and 2.5) as a function of λ, where the numbers
are averaged for 30 agent runs with 20 episodes each
as in (Singh and Sutton, 1996). For some reason, the
results reported here indicate 50% less steps than in
most other papers (except e.g. (Smart and Kaelbling,
2000) who have similar numbers as here), which
should be taken into consideration when comparing
results. Taking this difference into consideration, the
CMAC results shown in Figure 2 are consistent with
those in (Singh and Sutton, 1996). The results using
gradient-descent Sarsa(λ) and NRBF are significantly
better than those obtained with CMAC.
Figure 3 shows the average number of steps per
episode for the best-performing agent with α = 3.9
and λ = 0.9. Convergence to an average of 60 steps
0.0 0.2 0.4 0.6 0.8 1.0
100 150 200 250
Mountain−Car, CMAC and RBF
λ
Average Steps/Episode at best α
CMAC accumulating
CMAC replacing with reset
RBF accumulating
RBF replacing without reset
Figure 2: Average number of steps per episode for 30 agents
running 20 episodes as in (Singh and Sutton, 1996).
0 20 40 60 80 100
100 200 300 400 500 600
Episode
Average Steps/Episode
Figure 3: Average number of steps per episode for best-
performing agent (replacing trace, α = 3.9 and λ = 0.9).
per episode is achieved after about 40 episodes. This
is better than the ‘less than 100 episodes’ indicated in
(Abramson et al., 2003). The optimal number of steps
indicated in (Smart and Kaelbling, 2000) is 56 steps
so 60 steps per episode can be considered optimal due
to the continuing exploration caused by the -1 reward
on every step. Therefore the converged learning re-
sult is also as good as in (Abramson et al., 2003) and
(Schaefer et al., 2007). (Abramson et al., 2003) used
Learning Vector Quantization together with Sarsa in-
stead of using NRBF so the complexity of the learning
algorithm is similar to the one used in this paper. The
reward function provided more guidance towards the
goal than the one used here and a fixed starting point
was used instead of a random one. The neural net
used in (Schaefer et al., 2007) is more complex than
the one used here while a reward of +1 was given at
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
130
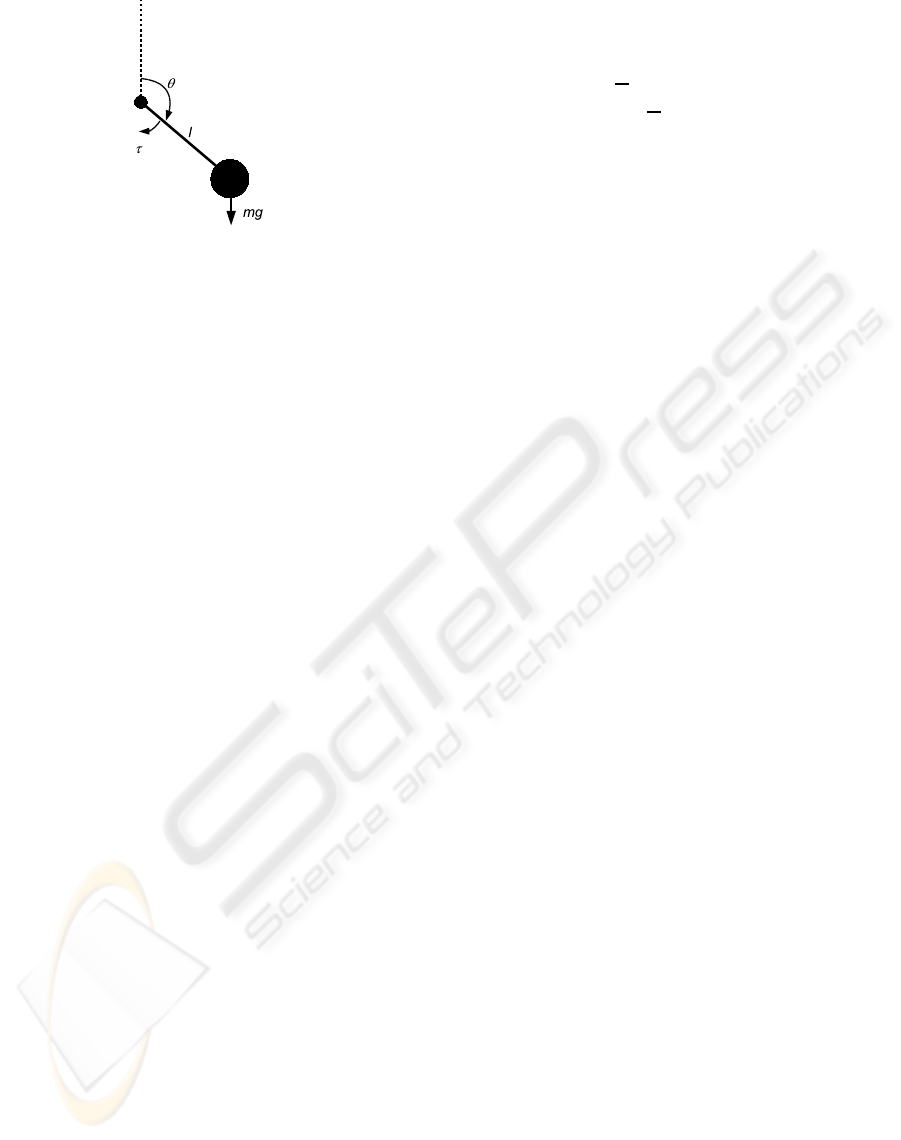
Figure 4: Pendulum swing-up with limited torque task.
the goal and zero otherwise. (Smart and Kaelbling,
2000) use an RBF-like neural network together with
Sarsa but no eligibility traces and a reward that is in-
versely proportionalto the velocity at goal (one if zero
velocity) and zero otherwise. Results are indicated
as a function of training steps rather than episodes
but a rough estimate would indicate that convergence
occurs after over 2000 episodes. The experimental
settings and the ways in which results are reported
in (Strens and Moore, 2002) do not make it possible
to compare results in a coherent way. In (Mahade-
van and Maggioni, 2007) convergence happens after
about 100 episodes, which is much slowerthan in Fig-
ure 3 despite the use of much more mathematically
and computationally complex methods. The results
in (Främling, 2007a) are clearly superior to all others
but they are obtained by having a parallel, hand-coded
controller guiding the initial exploration, which could
also be combined with gradient-descent Sarsa(λ) and
NRBF. These differences make it difficult to compare
results but the results shown in this paper are system-
atically better than comparable results reported in lit-
erature.
4.2 Pendulum Swing-up with Limited
Torque
Swinging up a pendulum to the upright position and
keeping it there despite an under-powered motor is a
task that has been used e.g in (Doya, 2000), (Schaal,
1997) and (Santamaría et al., 1998). The task descrip-
tion used here is similar to the one in (Doya, 2000).
There are two continuous state variables: the angle
θ and the angular speed
˙
θ. The agent chooses from
the two actions ±5
Nm
corresponding to clockwise and
anti-clockwise torque. The discount rate γ was set to
one. The system dynamics are defined as follows:
ml
2
¨
θ = −π
˙
θ+ mglsinθ + τ,θ ∈ [−π, π]
m = l = 1,g = 9.81,µ = 0.01,τ
max
= 5Nm
At the beginning of each episode θ is initialized to a
random value from [−π, π] and
˙
θ = 0. Every episode
lasted for 60 seconds with a time step ∆
t
= 0.02 using
Euler’s method. The performance measure used was
the time that |θ| ≤
pi
2
. The reward was r
1
= cosθ −
0.7, except when |θ| ≤
pi
5
where it was r
2
= r
1
−
˙
θ
.
Such a reward function encourages exploration when
the pendulum cannot be taken directly to the upright
position by the available torque. It also provides some
guidance to that zero is the ideal speed in the upright
position. This shaping reward remains less explicit
than the one used e.g. in (Schaal, 1997) and (Santa-
maría et al., 1998). This learning task is more diffi-
cult than in (Schaal, 1997) and (Doya, 2000) where
a model of the system dynamics either has been used
directly or learned by a model. 10×10 NRBF neu-
rons were used with regularly spaced centroids. An
affine transformation mapped the actual state values
from the intervals [−π,π] and [−1.5,1.5] (however,
angular speeds outside this interval are also allowed)
into the interval [0,1] that was used as~s.
Figure 5 shows the time that the pendulum re-
mains in the upright position for the best-performing
agent (replacing trace, α = 1.5 and λ = 0.4). An up-
time over 40 seconds signifies that the pendulum is
successfully balanced until the end, which occurs af-
ter about 10 episodes. In (Doya, 2000) a continu-
ous actor-critic model was used that is computation-
ally more complex than what is used in this paper.
A model-free agent in (Doya, 2000) started perform-
ing successfully after about 50 episodes but never
achieved a stable performance. The best results were
achieved by an agent with a complete model of the
system dynamics, which performed successfully after
about 10 episodes. However, such model-based re-
sults should not be compared with model-free meth-
ods like the one used in this paper. In (Schaal, 1997)
a model-based TD(λ) method was used that per-
formed successfully after about 100 episodes, so de-
spite the model-based approach the results are not as
good as those in Figure 5. Gradient-descent Sarsa(λ)
is used together with RBF networks in (Santamaría
et al., 1998) also for the case of continuous actions.
However, they used a reward function that guided
learning much more than the one used here. Their
instance-based agent that is computationally on the
same level as the NRBF net used here did not manage
to learn successfully, while the more complex case-
based agent did so. The case-based agents managed
to balance the pendulum after about 30 episodes but
due to a cut-off in the top of the result-showing graphs
it is difficult to assess the performance after that. In
any case, the results shown in this paper are system-
atically better than those compared with here, while
remaining simpler to use and computationally lighter.
LIGHT-WEIGHT REINFORCEMENT LEARNING WITH FUNCTION APPROXIMATION FOR REAL-LIFE
CONTROL TASKS
131

0 20 40 60 80 100
20 30 40 50
Episode
Average uptime in seconds
Figure 5: Average up-time for the best-performing agent in
seconds as a function of episode for pendulum task.
0.0 0.2 0.4 0.6 0.8 1.0
40 45 50 55
Pendulum, RBF
λ
Average up−time in seconds for best α
accumulating trace
replacing trace
Figure 6: Average up-time in seconds for pendulum task
with best α value as a function of λ. Error bars indicate one
standard error.
As shown in Figure 6, the replacing trace consistently
gives slightly better performance than the accumulat-
ing trace for this task. Learning results are also much
more sensitive to the value of the learning rate for the
accumulating trace than for the replacing trace.
4.3 Cart-Pole
One of the first uses of RL for the Cart-Pole task
was reported in (Barto et al., 1983). It is unknown
whether successful learning has been achieved with
model-free Sarsa(λ) on this task. An actor-critic ar-
chitecture was used in (Barto et al., 1983), (Kimura
and Kobayashi, 1998) and (Schneegaß et al., 2007).
Memory-based architectures were used in (Whitehead
and Lin, 1995) while (Schaal, 1997) uses initial su-
Figure 7: Cart-Pole task.
pervised learning for six episodes in order to provide
an approximately correct initial action-valuefunction.
Some kind of reward shaping is also employed in or-
der to simplify the learning task.
The task description used here is from (Barto
et al., 1983). There are four continuous state vari-
ables: the angle θ and angular speed
˙
θ of the pole and
the position x and velocity ˙x of the cart. The agent
chooses from the two actions ±10
N
corresponding to
right or left acceleration. The discount rate γ was
set to one and ε-greedy exploration with ε = 0.1 was
used. The system dynamics are:
¨
θ =
gsinθ
t
+ cosθ
t
h
−F
t
−ml
˙
θ
2
t
sinθ
t
+µ
c
sgn( ˙x
t
)
m
c
+m
i
−
µ
p
˙
θ
t
ml
l
h
4
3
−
mcos
2
θ
t
m
c
+m
i
¨x
t
=
F
t
+ ml
˙
θ
2
l
sinθ
t
−
¨
θ
t
cosθ
t
− µ
c
sgn( ˙x
t
)
m
c
+ m
m
c
= 1.0
kg
,m = 0.1
kg
,l = 0.5
m
,g = 9.81m/s
2
,
µ
c
= 0.0005,µ
p
= 0.000002,F
t
= ±10
N
Every episode started with θ = 0,
˙
θ = 0, x = 0, ˙x = 0
and lasted for 240 seconds or until the pole tipped
over (θ > 12
◦
) with a time step ∆
t
= 0.02 using Eu-
ler’s method. The reward was zero all the time except
when the pole tipped over, where a -1 ‘reward’ was
given. The NRBF network used 6 × 6 × 6 × 6 RBF
neurons with regularly spaced centroids. An affine
transformation mapped the actual state values into the
interval [0,1] as for the other tasks.
Table 1 indicates approximate numbers for how
many episodes were required before most agents have
succesfully learned to balance the pole. Compari-
son between the results presented in different sources
is particularly difficult for this task due to the great
variation between the worst and the best performing
agents. Anyway, the results presented here are at
least as good as in the literature listed here despite
the use of conceptually and computationally signifi-
cantly simpler methods in this paper. The only ex-
ception is (Mahadevan and Maggioni, 2007) that per-
forms well in this task, most probably due to a con-
siderably more efficient use of kernels in the parts of
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
132

Table 1: Approximate average episode when successful bal-
ancing occurs in different sources, indicated where avail-
able.
This paper 100
(Barto et al., 1983) 80
(Whitehead and Lin, 1995) 200
(Kimura and Kobayashi, 1998) 120
(Schneegaß et al., 2007) 100-150
(Lagoudakis and Parr, 2003) 100
(Mahadevan and Maggioni, 2007) 20
0.0 0.2 0.4 0.6 0.8
20 30 40 50 60 70 80 90
Cart−Pole, RBF
Average Steps/Episode at best α
Figure 8: Average up-time in seconds for Cart-Pole task
with best α value as a function of λ. Error bars indicate one
standard error.
the state space that are actually visited, rather than the
regularly spaced 6×6×6×6 RBF neurons used here,
of which a majority is probably never used. However,
the kernel allocation in (Mahadevan and Maggioni,
2007) requires initial random walks in order to obtain
samples from the task that allow offline calculation
of corresponding Eigen vectors and allocating ‘Proto-
Value Functions’ from them.
A challenge in interpreting the results of the
experiments performed for this paper is that the
agent ‘un-learns’ after a certain number of success-
ful episodes where no reward signal at all is received.
As pointed out in (Barto et al., 1983), this lack of
reward input slowly deteriorates the already learned
action-value function in critic-only architectures such
as Sarsa(λ). The results shown in Figure 8 include
this phenomenon, i.e. the average values are calcu-
lated for 200 episodes during which the task is suc-
cessfully learned but also possibly un-learned and re-
learned again.
The results shown in Figure 8 differ from those
of the previous tasks by the fact that the accumulat-
ing trace performs slightly better than the replacing
trace and that the parameter sensitivity is quite similar
for both trace types in this task. This difference com-
pared to the two previous tasks is probably due to the
delayed (and rare) reward that allows the eligibility
trace to decline before receiving reward, thus avoid-
ing weight divergence in equation 1. Further empir-
ical results from tasks with delayed reward are still
needed before declaring which eligibility trace type is
better.
5 CONCLUSIONS
Gradient-descent Sarsa(λ) is not a new method for
action-value learning with continuous-valued func-
tion approximation. Therefore it is surprising how lit-
tle empirical knowledge exists that would allow prac-
titioners to assess its usability compared with more
complex RL methods. The only paper of those cited
here that uses gradient-descent Sarsa(λ) is (Santa-
maría et al., 1998). The results obtained in this pa-
per show that at least for the three well-known bench-
mark tests used, gradient-descent Sarsa(λ) together
with NRBF function approximation tends to outper-
form all other methods while being the conceptually
and computationally most simple-to-use method. The
results presented here should provide a useful bench-
mark for future experimentsbecause they seemto out-
perform most previously reported results, even those
where a previously collected training set or a model
of the system dynamics was used directly or learned.
These results are obtained due to the linking of
different pieces together in an operational way. Im-
portant elements are for instance the choice of us-
ing NRBF and the normalisation of state values into
the interval [0,1] that simplifies finding suitable learn-
ing rates and r
2
values. The replacing eligibility
trace presented in (Främling, 2007b) is also more sta-
ble against learning parameter variations than the ac-
cumulating trace while giving slightly better perfor-
mance. Future directions of this work could con-
sists in performing experiments with more challeng-
ing tasks in order to see the limits of pure gradient-
descent Sarsa(λ) learning. In tasks where gradient-
descent Sarsa(λ) is not sufficient, combining it with
pre-existing knowledge as in (Främling, 2007a) could
be a solution for applying RL to new real-world con-
trol tasks.
REFERENCES
Abbeel, P., Coates, A., Quigley, M., and Ng, A. Y. (2007).
An application of reinforcement learning to aerobatic
helicopter flight. In Schölkopf, B., Platt, J., and Hoff-
LIGHT-WEIGHT REINFORCEMENT LEARNING WITH FUNCTION APPROXIMATION FOR REAL-LIFE
CONTROL TASKS
133

man, T., editors, Advances in Neural Information Pro-
cessing Systems 19, pages 1–8, Cambridge, MA. MIT
Press.
Abramson, M., Pachowicz, P., and Wechsler, H. (2003).
Competitive reinforcement learning in continuous
control tasks. In Proceedings of the International
Joint Conference on Neural Networks (IJCNN), Port-
land, OR, volume 3, pages 1909–1914.
Albus, J. S. (1975). Data storage in the cerebellar model ar-
ticulation controller (cmac). Journal of Dynamic Sys-
tems, Measurement and Control, September:228–233.
Barto, A., Sutton, R., and Anderson, C. (1983). Neuron-
like adaptive elements that can solve difficult learning
control problems. IEEE Trans. on Systems, Man, and
Cybernetics, 13:835–846.
Doya, K. (2000). Reinforcement learning in continuous
time and space. Neural Computation, 12:219–245.
Främling, K. (2004). Scaled gradient descent learning rate
- reinforcement learning with light-seeking robot. In
Proceedings of ICINCO’2004 conference, 25-28 Au-
gust 2004, Setubal, Spain, pages 3–11.
Främling, K. (2005). Adaptive robot learning in a non-
stationary environment. In Proceedings of the 13
th
European Symposium on Artificial Neural Networks,
April 27-29, Bruges, Belgium, pages 381–386.
Främling, K. (2007a). Guiding exploration by pre-existing
knowledge without modifying reward. Neural Net-
works, 20:736–747.
Främling, K. (2007b). Replacing eligibility trace for action-
value learning with function approximation. In Pro-
ceedings of the 15
th
European Symposium on Artifi-
cial Neural Networks, April 25-27, Bruges, Belgium,
pages 313–318.
Kimura, H. and Kobayashi, S. (1998). An analysis of
actor/critic algorithms using eligibility traces: Rein-
forcement learning with imperfect value functions. In
Proceedings of the 15
th
Int. Conf. on Machine Learn-
ing, pages 278–286.
Lagoudakis, M. G. and Parr, R. (2003). Least-squares pol-
icy iteration. Journal of Machine Learning Research,
4:1107–1149.
Mahadevan, S. and Maggioni, M. (2007). Proto-value func-
tions: A laplacian framework for learning represen-
tation and control in markov decision processes. J.
Mach. Learn. Res., 8:2169–2231.
Moore, A. (1991). Variable resolution dynamic program-
ming. efficiently learning action maps in multivari-
ate real-valued state-spaces. In Machine Learning:
Proceedings of the Eight International Workshop, San
Mateo, CA., pages 333–337. Morgan-Kaufmann.
Santamaría, J., Sutton, R., and Ram, A. (1998). Experi-
ments with reinforcement learning in problems with
continuous state and action spaces. Adaptive Behav-
ior, 6:163–217.
Schaal, S. (1997). Learning from demonstration. In
Advances in Neural Information Processing Systems
(NIPS), volume 9, pages 1040–1046. MIT Press.
Schaefer, A. M., Udluft, S., and Zimmermann, H.-G.
(2007). The recurrent control neural network. In Pro-
ceedings of 15
th
European Symposium on Artificial
Neural Networks, Bruges, Belgium, 25-27 April 2007,
pages 319–324. D-Side.
Schneegaß, D., Udluft, S., and Martinetz, T. (2007). Neu-
ral rewards regression for near-optimal policy identi-
fication in markovian and partial observable environ-
ments. In Proceedings of 15
th
European Symposium
on Artificial Neural Networks, Bruges, Belgium, 25-
27 April 2007, pages 301–306. D-Side.
Singh, S. and Sutton, R. (1996). Reinforcement learning
with replacing eligibility traces. Machine Learning,
22:123–158.
Smart, W. D. and Kaelbling, L. P. (2000). Practical rein-
forcement learning in continuous spaces. In Proceed-
ings of the Seventeenth 17
th
International Conference
on Machine Learning, pages 903–910. Morgan Kauf-
mann.
Strens, M. J. and Moore, A. W. (2002). Policy search us-
ing paired comparisons. Journal of Machine Learning
Research, 3:921–950.
Sutton, R. and Barto, A. (1998). Reinforcement Learning.
MIT Press, Cambridge, MA.
Tesauro, G. (1995). Temporal difference learning and td-
gammon. Communications of the ACM, 38:58–68.
Whitehead, S. and Lin, L.-J. (1995). Reinforcement learn-
ing of non-markov decision processes. Artificial Intel-
ligence, 73:271–306.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
134
