AN ONLINE BANDWIDTH SCHEDULING ALGORITHM FOR
DISTRIBUTED CONTROL SYSTEMS WITH MULTIRATE
CONTROL LOOPS
Saroja Kanchi
Department of Computer Science, Kettering University, Flint, MI 48504, U.S.A.
Juan Pimentel
Department of Electrical and Computer Engineering, Kettering University, Flint, MI 48504, U.S.A.
Keywords:
Control systems, control loops, scheduling, distributed systems.
Abstract:
In this paper, we present an online scheduling algorithm for communication in a distributed control system.
The packet size of the communication varies for each execution of the loop within certain bounds. We consider
systems with closed loops that restart immediately after the completion of an execution. Our algorithm is
based on priority of the loop and size of the communication packet. We demonstrate through simulation
that our algorithm generates a feasible schedule that minimizes average control delay over all the loops. Our
simulations demonstrate that this online schedule reduces average delay significantly compared to a-priori
schedules for distributed control systems. We demonstrate that bandwidth utilization is more efficient in case
of online scheduling.
1 INTRODUCTION
Distributed Control Systems are becoming popular
since they offer flexibility, modularity, speed and ef-
ficiency in designing a control system. Distributed
Control System is made up of large number of com-
ponents each of which performs a dedicated task and
also communicates with other components. Examples
of distributed control systems include officeand home
automation, aircraft and spacecraft systems and auto-
motive component systems. The tasks within the Dis-
tributed Control Systems have strict timing require-
ments on start times and completion times.
The performance of a distributed control system
depends not only on the performance of the individ-
ual components but also on the interaction between
components. Timing of the task completion and com-
munication pose significant challenges in designing
a Distributed Control Systems. Added to this com-
plexity is the issue of fault-tolerance and reliability.
Designing a-priori or static algorithms for distributed
control systems have been considered for a long time.
These algorithms do not take into consideration the
changing nature of interaction within the components
of the system or application specific requirements
of the control system. We propose an online band-
width scheduling algorithm for communication in a
distributed control system. This algorithm takes into
consideration the priority of each task within the sys-
tem and also size of each communication task. The
size of communication depends on the results of the
computation at each node of the system. Thus, we
are proposing a dynamic algorithm that addresses the
changing communication needs of the system.
The particular type of Distributed Control Sys-
tems we consider in this paper are those that consist
of control loops. In (Yepez et al., 2003) an algorithm
called the largest error first allocates bandwidth on the
basis of the loop that contains the largest error. But
the performance is not documented in the paper. In
(Velasco et al., 2004) provide a dynamic bandwidth
allocation algorithm based on adding a state variable
to the control system model for small control systems.
Their algorithm uses the performance of the control
system as a feed back mechanism for scheduling the
network. Our algorithm assumes an schedule that is
handled by the network controller.
There were several static real-time scheduling al-
gorithms designed for various real time tasks (San-
tos et al., 1997; Altenbernd and Hansson, 2004;
293
Kanchi S. and Pimentel J. (2008).
AN ONLINE BANDWIDTH SCHEDULING ALGORITHM FOR DISTRIBUTED CONTROL SYSTEMS WITH MULTIRATE CONTROL LOOPS.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 293-296
DOI: 10.5220/0001484302930296
Copyright
c
 SciTePress

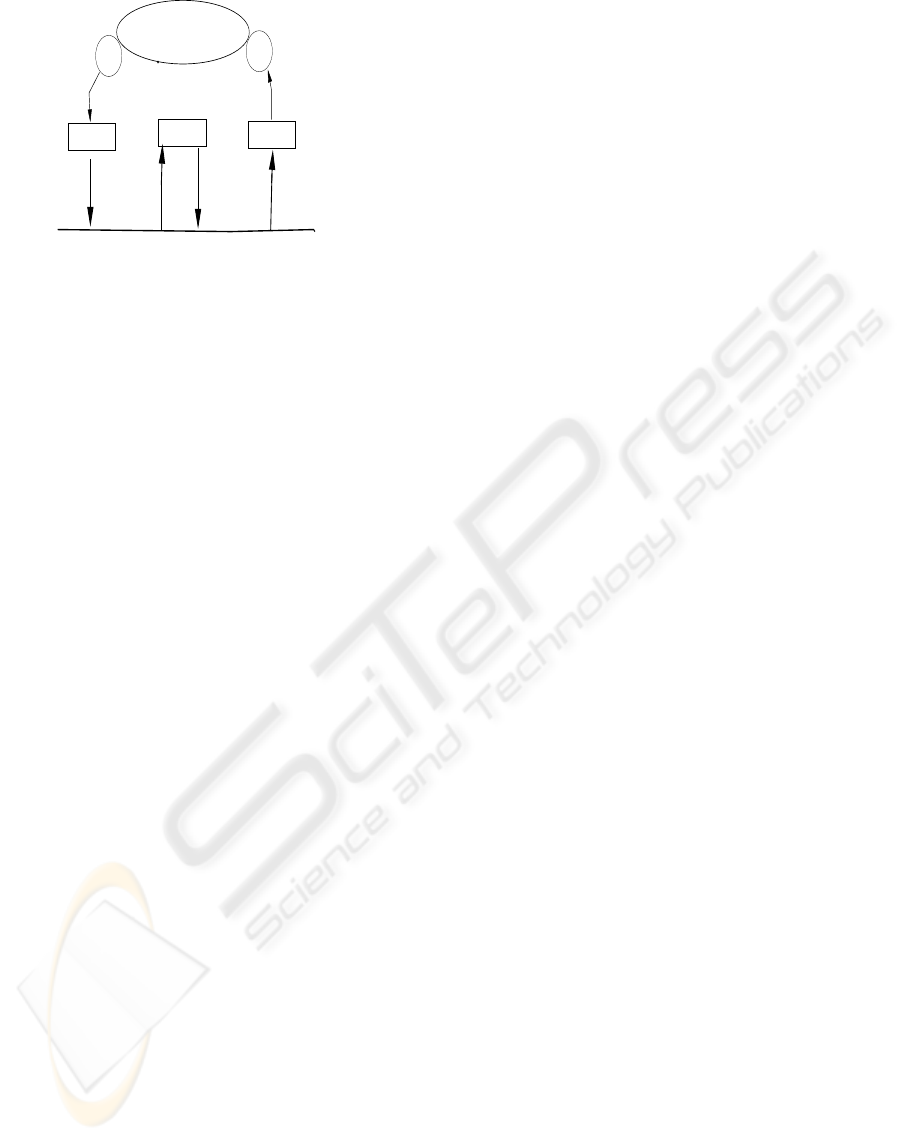
Controlled System
Sensor
Actuator
Compute Node
Actuator Node
Sensor Node
Communication
Network
Figure 1: Model of Control Loop.
Blazewicz and Ecker, 1994; Ramamritham, 1990).
Peng and Shin (Peng and Shin, 1989) provide a static
allocation of processors for periodic tasks that contain
both computation and communication. The commu-
nication imposes precedence constraints among the
tasks. The allocation does not allocate communica-
tion link and is static allocation. Xu (Xu, 1993) pro-
vides an algorithm for multiprocessor scheduling for
tasks with deadlines, release times, precedence and
exclusion constraints. Again this schedule provides
static schedule for processor assignment.
2 THE MODEL
We assume there are n control loops in the Distributed
Control System. Each loop contains a sensor node
that senses the values of certain variables. The sen-
sor then transmits the results of the sensed variables
over the network. Once the results of the sensor is
available the compute node then starts to compute its
algorithms. The output of the compute node is then
communicated over the network to the actuator node.
Since the loop is closed and the loops are multirate,
we assume that after the actuator triggers the neces-
sary components, the sensor nodes starts again at the
beginning of the loop. This system is illustrated in
Figure 1.
The three tasks of a control loop can be done in the
order of sensing, computation and actuation and then
the control loop begins at sensing again. Note that
there are three dedicated nodes at each loop. The sen-
sor node that converts the sensed signal into variable
values, the compute node that is dedicated to comput-
ing values, and actuator node that produces the de-
sired signal on the basis of computed values. Theses
nodes can work in parallel if desired.
Each control loops is represented as follows: S
k
,
C
k
and A
k
represent the sensor, compute and actua-
tor nodes for the k
th
control loop. There are several
types of possible delays in the execution of a con-
trol loop. The delay sensor node, compute node and
actuator node for the k
th
loop are denoted by s
k
, c
k
and a
k
respectively. It is assumed that the set of con-
trol loops of the system share the same communica-
tion channel. The communication delay are of two
types- The communication delay that is caused while
sending the sensed variables to the compute node over
the communication network is denoted by st
k
and the
communication delay caused due to transmission of
the computed values is denoted by ct
k
. Therefore, the
total control delay D
k
for the k
th
loop is denoted by
D
k
= s
k
+ st
k
+ c
k
+ ct
k
+ a
k
We assume that each loop in the system has a priority
given by p
k
. The control loops are closed and they
restart at a different rates. They restart as soon as an
execution of the loop is completed. The algorithm we
develop for scheduling the transmission of the results
of sensor and compute nodes has the goal of minimiz-
ing the average loop delay over the given set of loops
in the system. We assume that higher priority loops
(critical loops) execute more times than a non-critical
loop over a period of time.
Unlike earlier models of the problem where com-
munication packet size is assumed to be same, we
vary the packet size between given limits for each
execution For example, the packet size produced by
the sensor node S
k
varies between f(s
k
) and g(s
k
),
where f and g are linear functions. Our scheduling
therefore can take advantage of the actual packet size
of the communication rather than a a-priori schedul-
ing of the communication independent of the packet
size. This avoids over allocation of the communica-
tion channel for the control loop.
2.1 Algorithm for Bandwidth Allocation
for Control Loops with Priority
For each control loop k, we are given the times s
k
,
c
k
and a
k
. These values do not change over multiple
executions of the loops. However, the values st
k
, ct
k
change depending the results produced by sensor and
communication nodes. The transmission time needed
on the communication channel is proportional to st
k
and ct
k
respectively. If a loop is ready to transmit
sensor variables, we set the next transmission length
to st
k
. If the loop ready to transmit computed values
we set the next transmission length to ct
k
. At any
point of time, a set of loops which we call ready
loops will be ready to transmit either the results of
the sensor node or the results of the compute node.
We use the following algorithm to schedule the
communication channel
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
294

At a time t,
For each time t, Repeat until all loops are scheduled
1) Find the loop(s) that has the highest priority
2) Among the loops with highest priority find the loop
that has the lowest next transmission length
3) Schedule the transmission of this loop
It is important to note that all ready loops that are
ready a a particular point of time are scheduled to-
gether. That is, the same high priority loop cannot
repeatedly use the channel thus reducing the average
waiting time over all loops. This technique avoids
the well known problem of starvation of low priority
loops.
It is important to note that the selection of one
among several loops of same priority is based on
transmission length and the one with the shortest
length is chosen. This is in tune in Shortest Job
First scheduling which is the optimal algorithm for
scheduling jobs on a single processor.
2.2 Algorithm for Bandwidth Allocation
for Control Loops with Equal
Priority
If the control loops have no assigned priority then we
cannot use the transmission alone as a measure since
deadline for each loop may not be met. Therefore, we
use the following algorithm for control systems that
do no have priority of loops.
At a time t,
For each time t, repeat until all loops are scheduled
Find the loop(s) that has the lowest next burst time.
The next-burst-time for control loop k is defined as
next-burst-time = st(k) + c(k)
if the communication desired is transmission of sensor values
next-burst-time = ct(k) +a_k+s(k) if the
communication desired if transmission of computed values
End
In this case, the delay of control loops is roughly
speaking, inversely proportional to the length of the
loop and therefore, the average control delay is mini-
mized for any set of loops.
3 SIMULATION
The simulation was done using a set of control loops
with the following parameters for each control loop:
sensorLow - low value of the sensor node processing
time
sensorHigh - high value of the sensor node processing
time
computeLow - low value of the compute node pro-
cessing time
computeHigh - high value of the compute node pro-
cessing time
actuationLow - low value of the actuation node pro-
cessing time
actuationHigh - high value of the actuation node pro-
cessing time
The s
k
, c
k
and a
k
were randomly generated to be
between the corresponding low and high values. For
loop, the following parameters were used:
f(s) - equation that generates the packet length for
sensor variable communication based on the sensor
processing time. This equation was linear in s.
g(c) - similar to the above and generates the
packet length for communication of the compute val-
ues
The functions f and g are randomly computed on-
line. That is, for each execution of the loop.
The most impressive results of the simulation is
that the algorithm produces a feasible schedule and
takes advantage of the fact that communication chan-
nel is scheduled as the packets become available. The
same algorithm can also handle loops with varying
priority if the control system uses a feedback mecha-
nism for varying priority.
The simulation results specifically demonstrate
the following. Figure 2 demonstrates that for loops
of distinct priority, that is 1-10, 1 being the highest
priority and 10 being the lowest priority, the schedul-
ing algorithm that is feasible and that higher the pri-
ority, lower the waiting time. Figure 3 demonstrates
the same for loops with random priority.
Figure 4-5 demonstrate that for a system with con-
trol loops with no priority, the waiting times were
proportional to the length of the loops, thus reducing
the overall control delay compared to any other algo-
rithm.
Figure 6-7 demonstrate the execution rate of the
control loops. Note that, the higher priority loops
have higher execution rate than that of lower priority
loops. To study the execution rate, the sensor times,
the compute times and actuation times were set to be
alike and f and g were set to a fixed δ.
1 2 3 4 5 6 7 8
0
10
20
30
40
50
60
70
Priorities: Lower number indicates higher priority
Average Waiting Time in milliseconds
Figure 2: Control Loop priority versus Average Waiting
Time.
AN ONLINE BANDWIDTH SCHEDULING ALGORITHM FOR DISTRIBUTED CONTROL SYSTEMS WITH
MULTIRATE CONTROL LOOPS
295

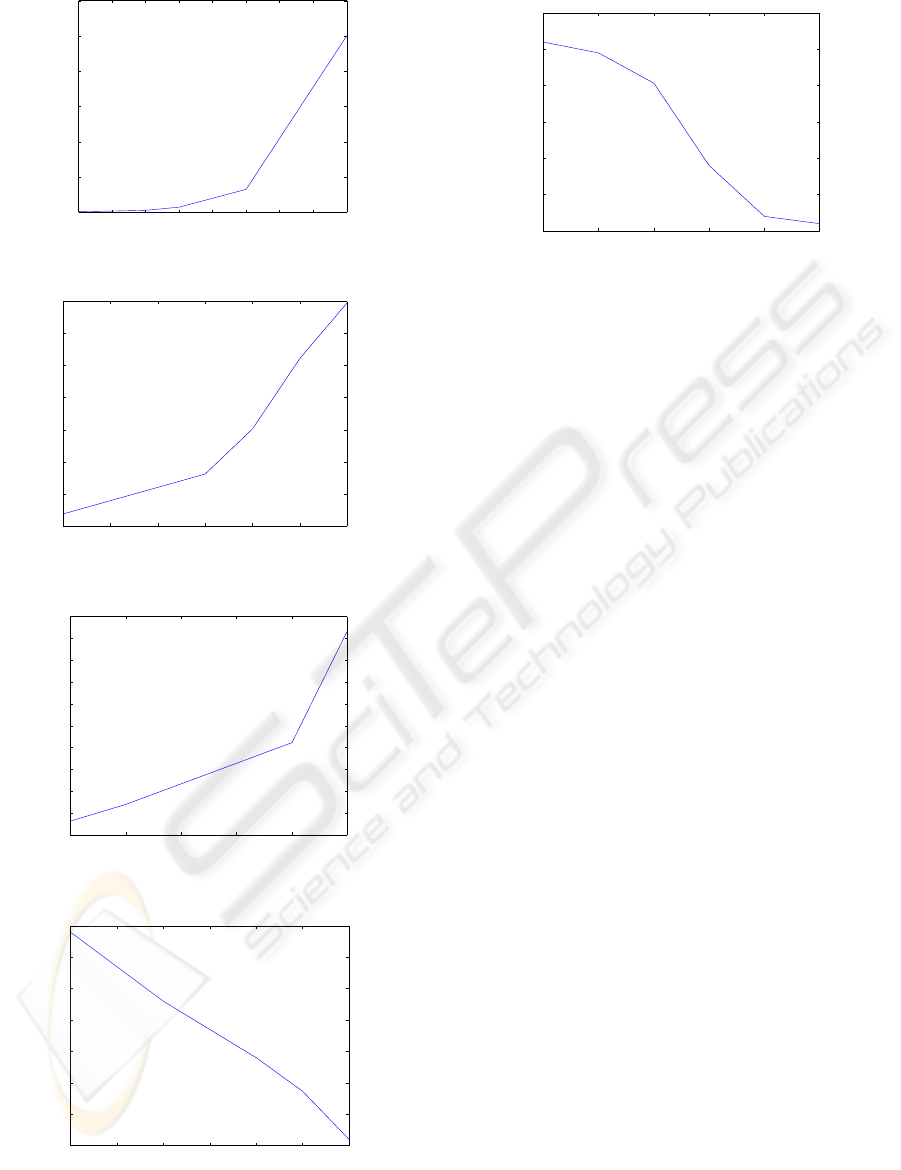
2 3 4 5 6 7 8 9 10
0
200
400
600
800
1000
1200
Priorities: Lower number indicates higher priority
Average Waiting Time in milliseconds
Figure 3: Control Loop priority versus Average Waiting Time with random priority for loop
Figure 3: Control Loop priority versus Average Waiting
Time with random priority for loops.
5 6 7 8 9 10 11
0
5
10
15
20
25
30
35
Sensor nodes times s(k) in milliseconds
Average Waiting Time in milliseconds
Figure 4: Sensor Node time versus average time to transmit
sensor variables.
7 8 9 10 11 12
0
5
10
15
20
25
30
35
40
45
50
Time spent at compute nodes c(k) in milliseconds
Waiting Time in milliseconds
Figure 5: Compute Node time versus average time to transmit computed results
Figure 5: Compute node time versus average time to trans-
mit computed results.
19 20 21 22 23 24 25
5
10
15
20
25
30
35
40
total time for the control loop execution
Number of times the loop executes in 1000 units of time
Figure 6: Control Loop Length versus Execution Rate for Equal Prioirity Loops
Figure 6: Control Loop Length versus Execution Rate for
Equal Priority Loops.
1 2 3 4 5 6
0
5
10
15
20
25
30
Priority of the Control Loop
Number of times the loop executes in 1000 units of time
Figure 7: Priority versus Execution Rate for UnEqual Prioirity Loops
Figure 7: Priority versus Execution Rate for UnEqual Pri-
ority Loops.
4 CONCLUSIONS
In this paper we have a dynamic scheduling algo-
rithm for control loops that takes into consideration
the changing nature of communication needs within
control systems. The algorithm handles loops of dif-
ferent priorities and different execution rates. The al-
gorithm produces a feasible schedule and produces
minimal control delay.
REFERENCES
Altenbernd, P. and Hansson, H. (2004). The slack method:
A new method for static allocation of hard real-time
tasks. Real-Time Systems, 15(2):103–130.
Blazewicz, J. and Ecker, K. (1994). Multiprocessor task
scheduling with resource requirements. Real Time
Systems, 6:37–53.
Peng, D.-T. and Shin, K. G. (1989). Static allocation of
periodic tasks with precedence constraints distributed
real-time systems. 9th International Conference on
Distributed Computing Systems,, pages 190–198.
Ramamritham, K. (1990). Allocation and scheduling of
complex periodic tasks. Proceedings of 10th Interna-
tional Conference on Distributed Computing Systems,
pages 108–115.
Santos, J., Ferro, E., Orozco, J., and Cayssials, R. (1997).
A heuristic approach to the multitask-multiprocessor
assignment problem using the empty-slots method.
Real-Time Systems, 13(2):167–199.
Velasco, M., Fuertes, J. M., Lin, C., Marti, P., and Brandt,
S. (2004). A control approach to bandwidth manage-
ment in networked control systems. Proc. 30th IEEE
IECON.
Xu, J. (1993). Multiprocessor scheduling of processes with
release times, deadlines, precedence, and exclusion
relations. IEEE Transactions on Software Engineer-
ing, 19(2):139–154.
Yepez, J., Marti, P., and Fuertes., J. M. (2003). Control
loop scheduling paradigm in distributed control sys-
tems. IECON ’03. The 29th Annual Conference of the
IEEE, 2:1441– 1446.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
296