DIRECTIONAL CHANGE IN A PRIORI ANTI-WINDUP
COMPENSATORS VS. PREDICTION HORIZON
Dariusz Horla
Poznan University of Technology, Institute of Control and Information Engineering
Division of Control and Robotics, ul. Piotrowo 3a, 60-965, Poland
Keywords:
Directional change, windup phenomenon, optimal control, linear matrix inequalities, predictive control.
Abstract:
The paper presents the correspondence in between directional change and anti-windup phenomenon with re-
spect to a priori anti-windup compensator on the basis of MPC (simulation results include plants with not equal
number of inputs and outputs). It shows what is the excess of directional change for consecutive predictions
of control vectors for a given prediction horizons.
1 INTRODUCTION
Taking control limits into consideration is necessary
to achieve high performance of the designed con-
trol systems (Horla, 2006b). There are two ways in
which one can consider possible constraints at syn-
thesis of controllers. In the first approach, imposing
constraints during the design procedure of the con-
troller usually leads to difficulties with obtaining ex-
plicit form of control laws, apart from very simple
cases. The other way is to assume the system is fully
linear and, subsequently, having designed the con-
troller for unconstrained system (by means of opti-
misation, using Diophantine equations, etc) – impose
constraints, what would require additional changes in
control system due to presence of constraints (Horla,
2007b; Öhr, 2003; Peng et al., 1998).
The situation when because of constraints internal
controller states do not correspond to the actual sig-
nals present in the control systems is referred in the
literature as windup phenomenon (Öhr, 2003). One
can expect inferior performance because of infeasibil-
ity of computed (unconstrained) control signals when
control limits are not taken into account.
A few methods of compensating the windup phe-
nomenon from SISO framework work well enough in
the case of multivariable systems (Öhr, 2003; Wal-
gama and Sternby, 1993). In such a case, apart from
the windup phenomenon itself, one can also observe
directional change in the control vector due to differ-
ent implementations of constraints, what could affect
direction of the unconstrained control vector (Horla,
2004; Horla, 2007a).
The other problem is, in general form, decou-
pling, with respect to not equal number of control sig-
nals and output signals, when control direction corre-
sponds not only to input principal directions or maxi-
mal directional gain of the transfer function matrix,
but also to the degree of decoupling (Albertos and
Sala, 2004; Maciejowski, 1989).
The problem of directional change has been ini-
tially discussed in (Walgama and Sternby, 1993). The
paper (Horla, 2007a) defined the connection of direc-
tional change problem with anti-windup compensa-
tion (AWC) for systems with equal numer of inputs
and outputs.
The current paper has been given rise by re-
search carried out in (Horla, 2004; Horla, 2007a;
Horla, 2007b) and extends the understanding of anti-
windup compensation to non-square systems with
imposed constraints, comparing control performance
with optimisation-based approach, related to MPC
(Camacho and Bordons, 1999; Doná et al., 2000; Ma-
ciejowski, 2002) that is widely-spread and applied in
the industry. In the paper, the problem of directional
change has been studied with respect to optimal a pri-
ori anti-windup compensation and different predic-
tion horizons.
2 A PRIORI AWC
One can perform anti-windup compensation by incor-
porating AWC implicitly into the controller. In order
to use all the advantages of such an approach (as op-
timality of the solution, no need to design decoupling
stages, etc.), let the optimal constrained control vector
108
Horla D. (2008).
DIRECTIONAL CHANGE IN A PRIORI ANTI-WINDUP COMPENSATORS VS. PREDICTION HORIZON.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 108-113
DOI: 10.5220/0001485301080113
Copyright
c
 SciTePress

follow from
u
⋆
t
: J
t
(u
⋆
t
) = inf
u
t
∈D(J
t
)
n
J
t
(u
t
)
o
, (1)
with constraints
|u
j,i,t
| ≤ α
j
, (2)
where α
j
is an amplitude constraint of the i–th ele-
ment of control vector, and u
j,t
, D(J
t
) is the set of all
control vectors such that J
t
has a finite value,
u
t
=





u
1,t
u
2,t
.
.
.
u
m,t





, (3)
and u
j,t
(1 ≤ j ≤ m) comprises sequences of control
actions applied to the j–th input with control horizon
N
u
(Horla, 2006a).
The controller is responsible for tracking given
reference (implicit model) output vector r
M,t
with y
t
minimising
J
t
=
p
∑
k=1
d+N
u
−1
∑
l=d
(r
M, k,t+l
− y
k,t+l
)
2
, (4)
which can be presented in the sense of L
2
norm as
J
t
=



r
M,t+d
− ˆy
t+d
−
ˆ
ˆy
t+d



2
2
, (5)
where
r
M,t+d
=





r
M, 1,t+d
r
M, 2,t+d
.
.
.
r
M, p,t+d





(6)
comprises vectors including reference signals known
for d + N
u
− 1 steps in advance.
The vector of prediction of plant response forced
by the sought control sequence is computed in an it-
erative manner
ˆy
t+d
=






ˆy
1,t+d
ˆy
2,t+d
.
.
.
ˆy
p,t+d






, (7)
where ˆy
i,t+d
= Gu
t
, and G comprises matrices of
plant impulse response samples.
The controller is to search for control vectors u
j,t
with 1 ≤ j ≤ m, each of them being control sequences
applied to the j–th input {u
j,t
, u
j,t+1
, ..., u
j,t+N
u
−1
}
in horizon N
u
> 0. Based on the superposition rule,
the decay-response vector
ˆ
ˆy
t+d
subject to initial con-
ditions u
t−k
(k ≥ 0) is computed iteratively alike.
Having expressed (4) as
J
t
=

Gu
t
+
ˆ
ˆy
t+d
−r
M,t+d

T

Gu
t
+
ˆ
ˆy
t+d
−r
M,t+d

, (8)
minimisation subject to constraints is equivalent to
(Boyd et al., 1994; Boyd and Vandenberghe, 2004)
minγ
s.t.






I ⋆
u
T
t
(G
T
G)
1/2




γ− (r
M,t+d
−
ˆ
ˆy
t+d
)
T
×
×(r
M,t+d
−
ˆ
ˆy
t+d
)+
+2(r
M,t+d
−
ˆ
ˆy
t+d
)
T
Gu
t










≥ 0,
diag
n
F
(1,1)
, ... , F
(1,m)
o
≥ 0 ≥ 0,
diag
n
F
(2,1)
, ... , F
(2,m)
o
≥ 0,
(9)
where the last to LMIs define upper and lower bounds
of u
t
, and ⋆ is a symmetrical entry.
3 SIMULATION STUDIES
The following multivariable CARMA plant model
will be of interest
A(q
−1
)y
t
= B(q
−1
)u
t−d
, (10)
with left co-prime polynomial matrices A(q
−1
),
B(q
−1
), delay d = 1, with y
t
∈ R
p
as the output vec-
tor, u
t
∈ R
m
is the constrained control vector (v
t
∈
R
m
will denote unconstrained control vector). The
considered plants are assumed to be cross-coupled:
• P1 (m = 2, p = 2)
A(q
−1
) = I+

0.8 −0.1
0.4 −1.0

q
−1
+
+

−0.49 −0.10
0.10 0.25

q
−2
,
B(q
−1
) =

1.0 0.3
0.5 0.8

,
• P2 (m = 3, p = 2)
A(q
−1
) = I+

0.8 −0.1
0.4 −1.0

q
−1
+
+

−0.49 −0.10
0.10 0.25

q
−2
,
B(q
−1
) =

1.0 0.2 0.3
0.5 0.3 0.8

,
DIRECTIONAL CHANGE IN A PRIORI ANTI-WINDUP COMPENSATORS VS. PREDICTION HORIZON
109

• P3 (m = 2, p = 3)
A(q
−1
) = I +


−0.7 0.0 0.1
−0.1 −0.8 0.2
0.1 0.0 −0.8


q
−1
+
+


−0.1 0.0 0.0
0.0 0.1 0.0
0.0 0.0 0.5


q
−2
,
B(q
−1
) =


1.0 0.1
0.2 1.0
0.5 −0.1


.
The reference vector is pre-filtered by implicit refer-
ence model with characteristic polynomial matrix
A
M
(q
−1
) = (1− 0.5q
−1
)I
p×p
,
what corresponds to closed-loop tracking with dy-
namics described by A
M
(q
−1
).
Evaluation of control performance connected with
anti-windup compensation quality requires following
performance indices to be introduced:
J
1
=
1
N
p
∑
i=1
N
∑
t=1
|r
i,t
− y
i,t
|, (11)
J
2
=
1
N
p
∑
i=1
N
∑
t=1
(r
i,t
− y
i,t
)
2
, (12)
ϕ
i
=
1
N
N
∑
t=1
|ϕ(v
t,i
) − ϕ(u
t,i
)| [
◦
], (13)
ϕ
2
i
=
1
N
N
∑
t=1
(ϕ(v
t,i
) − ϕ(u
t,i
))
2
, (14)
where (11) corresponds to mean absolute tracking er-
ror of p outputs, (13) is a mean absolute direction
change in between computed and constrained control
vector, and ϕ(i) denotes angle measure of control vec-
tor sequence in prediction horizon N
u
= i.
4 SIMULATION RESULTS
For plants P1 and P2 the reference vectors comprise
piecewise constant reference signals, whereas for P3
the third output is to be kept at zero at all times, what
is difficult when there is a inferior number of control
inputs in comparison with plant outputs.
Numerical results of performed simulations have
been presented in Tables 1 and 2. The first set of sim-
ulations tested to what excess the directional change
phenomenon will take place for plants P1–P3 and dif-
ferent prediction horizon.
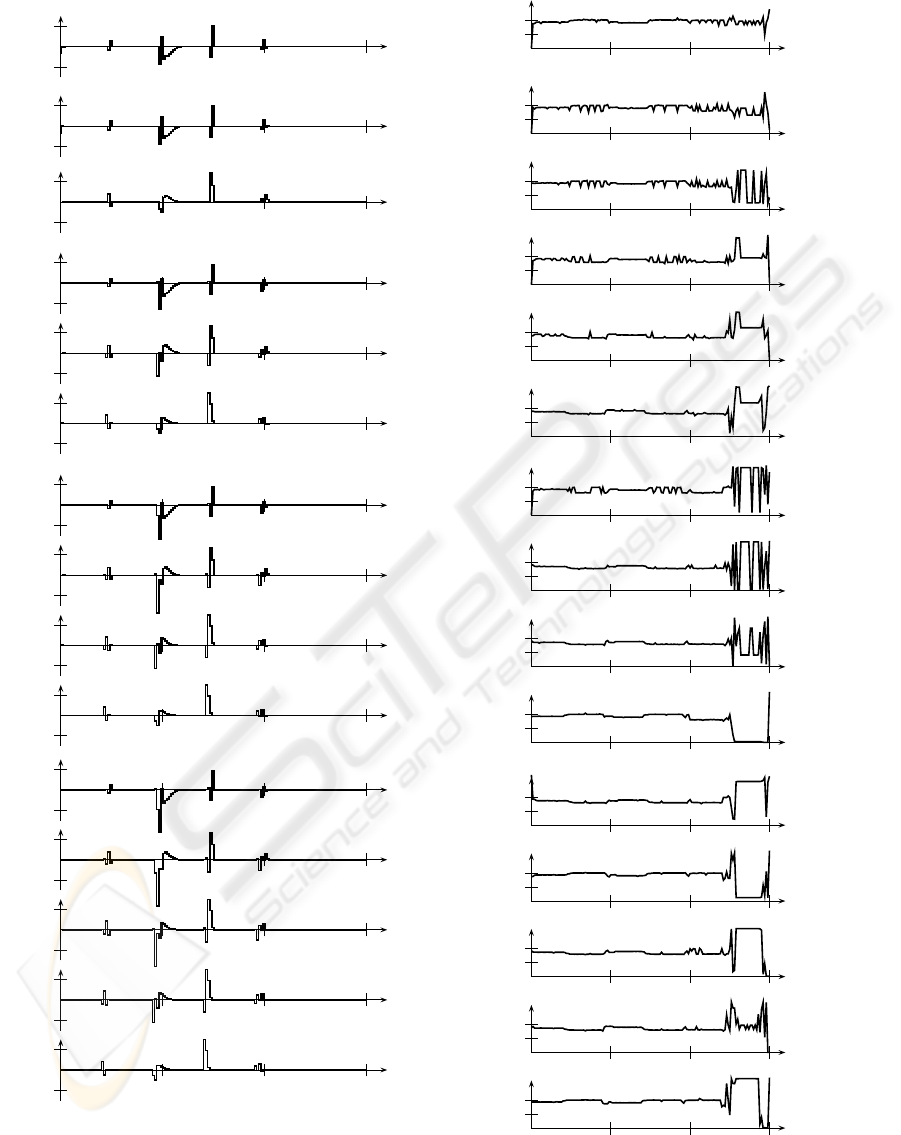
As it can be seen from Table 1a and Figures 1 and
4, for P1, the greatest directional change (with respect
to unconstrained control vector generated at the same
time instant, but not applied) takes place in the cur-
rent sample. The greater the prediction horizon, the
smaller the directional change becomes. Since a mean
angle deviations is approx. 1
◦
then, one can say that
constrained control vector is close to the computed
unconstrained control vector. This might also take
place because of equal number of inputs and outputs,
what leads to easier decoupling.
In the case of P2 (Tab. 1b, Fig. 2, 5), mean an-
gle deviation is near the right angle, what corresponds
to to normal vectors with the third component un-
changed, i.e. rotation with respect to a fixed axis.
This might be be connected with plant principal di-
rections and with the need to decouple outputs from
inputs. Since the number of control inputs is greater
than plant outputs, the excessive change in direction
is needed, because one can obtain better tracking per-
formance than for m = p = 2.
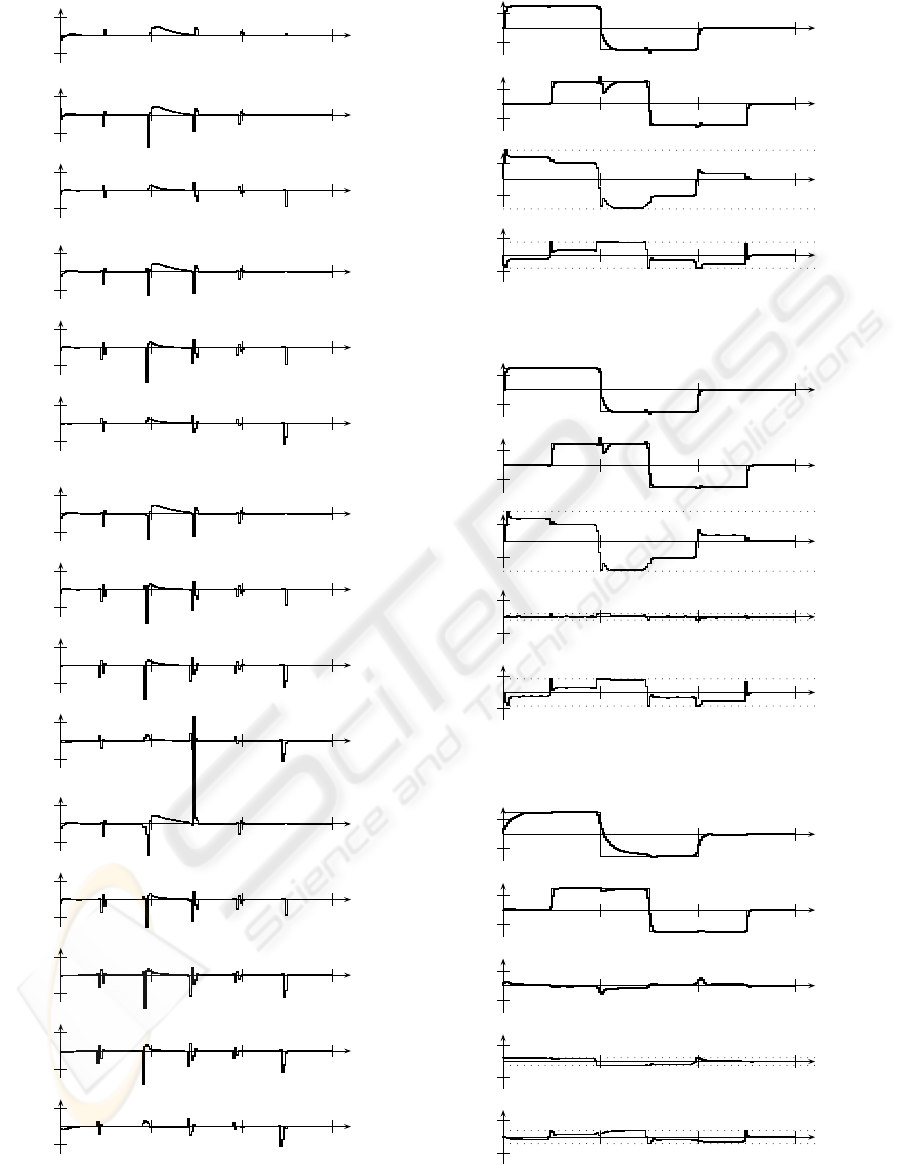
If the plant has insufficient number of control in-
puts (P3, Tab. 2b, Fig. 3, 6), it is impossible to as-
sure high control performance and one has to cope
with potential problem of uncontrollable modes. As
it can be seen, the speed of transients has been re-
duced, what lead to better decoupling, aiding anti-
windup compensation. In such a case, often direc-
tional change is a result of the need of decoupling.
For the case of no directional change requirement
(Tab. 2), such a regime of work (present in some ap-
plications in robotics, or e.g. in tracking, (Öhr, 2003)),
results in inferior control performance. For P1 and in-
creasing N
u
one obtains performance degradation, for
P2 the closed-loop system becomes unstable (in order
to decouple, the controller would have to alter control
direction) the only improvement can be observed in
the case of P3 because of m < p (where some cou-
pling is always present and results in proportions be-
tween control vector components that controller has
to abide to).
5 SUMMARY
As it has been shown in the paper, the problem of di-
rectional change can be presented in a different way
for plants with m 6= p than in (Horla, 2007a; Walgama
and Sternby, 1993). Not allowing directional change,
may cause instability in the case of unstable plants
(see P2), whereas for the other cases it degrades con-
trol performance.
Altering control direction is related to decoupling,
thus one can expects problems with performance for
m > p and good control quality for m < p when com-
ponents of control vector must be kept in proportion
(e.g., in a circular shape cutting task) at all times.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
110

Table 1: a) p = 2, m = 2, b) p = 2, m = 3, c) p = 3, m = 2.
a) N
u
= 1 N
u
= 2 N
u
= 3 N
u
= 4 N
u
= 5
J
1
0.6354 0.6144 0.6034 0.5951 0.5911
J
2
1.9002 1.7126 1.6219 1.5683 1.5338
ϕ
1
0.7171 0.8604 1.4556 1.5468 1.6631
ϕ
2
0.7736 0.9795 1.1555 1.3119
ϕ
3
0.7398 1.0107 1.1649
ϕ
4
0.7299 0.9942
ϕ
5
0.7207
ϕ
2
1
11.8327 9.5201 111.7057 115.1060 124.3589
ϕ
2
2
10.2881 13.1625 19.5663 25.4658
ϕ
2
3
10.6466 15.1063 20.8268
ϕ
2
4
10.6025 14.9204
ϕ
2
5
10.5455
b) N
u
= 1 N
u
= 2 N
u
= 3 N
u
= 4 N
u
= 5
J
1
0.3535 0.3518 0.3560 0.3581 0.3585
J
2
0.7373 0.6985 0.6914 0.6923 0.6931
ϕ
1
95.1171 89.5872 89.5007 96.3644 93.5828
ϕ
2
88.0821 90.1826 88.2265 86.9010
ϕ
3
88.9365 82.4423 91.6918
ϕ
4
79.6011 87.4887
ϕ
5
102.5099
ϕ
2
1
9138.6 8218.2 8306.7 10250.0 9549.4
ϕ
2
2
8341.1 8477.1 8938.1 8517.1
ϕ
2
3
8429.2 7331.5 9513.0
ϕ
2
4
7492.2 8101.1
ϕ
2
5
11619.6
c) N
u
= 1 N
u
= 2 N
u
= 3 N
u
= 4 N
u
= 5
J
1
1.3293 1.2364 1.1721 1.1422 1.1407
J
2
1.8375 1.3703 1.2450 1.1629 1.1177
ϕ
1
2.5244 3.6052 3.7189 3.8635 5.8012
ϕ
2
1.8646 3.0450 3.2257 3.2991
ϕ
3
2.1306 3.4264 3.6449
ϕ
4
2.0898 3.4420
ϕ
5
2.2384
ϕ
2
1
37.0812 109.3184 95.4019 106.2623 687.9498
ϕ
2
2
33.4335 116.5809 121.1664 106.5284
ϕ
2
3
49.0232 135.6229 141.8349
ϕ
2
4
46.1047 131.0049
ϕ
2
5
47.5444
Table 2: no directional change, a) p = 2, m = 2, b) p = 2,
m = 3, c) p = 3, m = 2 (− denotes unstable closed-loop
system).
a) N
u
= 1 N
u
= 2 N
u
= 3 N
u
= 4 N
u
= 5
J
1
0.8846 0.8994 0.8674 0.8914 0.8975
J
2
2.4978 2.6290 2.3793 2.3365 2.2729
b) N
u
= 1 N
u
= 2 N
u
= 3 N
u
= 4 N
u
= 5
J
1
9.5249 11.1171 10.6376 − −
J
2
36.8874 77.8512 62.5581 − −
c) N
u
= 1 N
u
= 2 N
u
= 3 N
u
= 4 N
u
= 5
J
1
1.4536 1.4110 1.3620 1.3450 1.3510
J
2
1.9418 1.6632 1.5240 1.4352 1.4242
REFERENCES
Albertos, P. and Sala, A. (2004). Multivariable Control Sys-
tems. Springer-Verlag, London, United Kingdom.
Boyd, S., Ghaoui, L. E., Feron, E., and Balakrishnan, V.
(1994). Linear Matrix Inequalities in System and Con-
trol Theory. Society for Industrial and Applied Math-
ematics, Philadelphia, United States of America, 3rd
edition.
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press, United Kingdom.
Camacho, E. and Bordons, C. (1999). Model Predictive
Control. Springer-Verlag, United Kingdom.
Doná, J. D., Goodwin, G., and Seron, M. (2000). Anti-
windup and model predictive control: Reflections and
connections. European Journal of Control, 6(5):455–
465.
Horla, D. (2004). Directional change and anti-windup com-
pensation for multivariable systems. Studies in Au-
tomation and Information Technology, 28/29:53–68.
Horla, D. (2006a). LMI-based multivariable adaptive pre-
dictive controller with anti-windup compensator. In
Proceedings of the 12th IEEE International Confer-
ence MMAR, pages 459–462, Miedzyzdroje.
Horla, D. (2006b). Standard vs. LMI approach to a con-
vex optimisation problem in multivariable predictive
control task with a priori anti-windup compensator. In
Proceedings of the 18th ICSS, pages 147–152, Coven-
try.
Horla, D. (2007a). Directional change and windup phe-
nomenon. In Proceedings of the 4th IFAC Interna-
tional Conference on Informatics in Control Automa-
tion and Robotics, pages CD–ROM, Angers, France.
Horla, D. (2007b). Optimised conditioning technique for
a priori anti-windup compensation. In Proceedings of
the 16th International Conference on Systems Science,
pages 132–139, Wrocław, Poland.
Maciejowski, J. (1989). Multivariable Feedback Design.
Addison-Wesley Publishing Company, Cambridge,
United Kingdom.
Maciejowski, J. (2002). Predictive Control with Con-
straints. Pearson Education Limited, United King-
dom.
Öhr, J. (2003). Anti-windup and Control of Systems with
Multiple Input Saturations: Tools, Solutions and Case
Studies. PhD thesis, Uppsala University, Uppsala,
Sweden.
Peng, Y., Vran
ˇ
ci
´
c, D., Hanus, R., and Weller, S. (1998).
Anti-windup designs for multivariable controllers.
Automatica, 34(12):1559–1565.
Walgama, K. and Sternby, J. (1993). Contidioning tech-
nique for multiinput multioutput processes with input
saturation. IEE Proceedings-D, 140(4):231–241.
DIRECTIONAL CHANGE IN A PRIORI ANTI-WINDUP COMPENSATORS VS. PREDICTION HORIZON
111

50 100 150
0
20
−20
ϕ
1,t
t
a)
50 100 150
0
20
−20
ϕ
1,t
t
b)
50 100 150
0
20
−20
ϕ
2,t
t
50 100 150
0
20
−20
ϕ
1,t
t
c)
50 100 150
0
20
−20
ϕ
2,t
t
50 100 150
0
20
−20
ϕ
3,t
t
50 100 150
0
20
−20
ϕ
1,t
t
d)
50 100 150
0
20
−20
ϕ
2,t
t
50 100 150
0
20
−20
ϕ
3,t
t
50 100 150
0
20
−20
ϕ
4,t
t
50 100 150
0
20
−20
ϕ
1,t
t
e)
50 100 150
0
20
−20
ϕ
2,t
t
50 100 150
0
20
−20
ϕ
3,t
t
50 100 150
0
20
−20
ϕ
4,t
t
50 100 150
0
20
−20
ϕ
5,t
t
Figure 1: p = 2, m = 2, a) N
u
= 1, b) N
u
= 2, c) N
u
= 3,
d) N
u
= 4, e) N
u
= 5.
0 50 100 150
0
50
100
ϕ
1,t
t
a)
0 50 100 150
0
50
100
ϕ
1,t
t
b)
0 50 100 150
0
50
100
ϕ
2,t
t
0 50 100 150
0
50
100
ϕ
1,t
t
c)
0 50 100 150
0
50
100
ϕ
2,t
t
0 50 100 150
0
50
100
ϕ
3,t
t
0 50 100 150
0
50
100
ϕ
1,t
t
d)
0 50 100 150
0
50
100
ϕ
2,t
t
0 50 100 150
0
50
100
ϕ
3,t
t
0 50 100 150
0
50
100
ϕ
4,t
t
0 50 100 150
0
50
100
ϕ
1,t
t
e)
0 50 100 150
0
50
100
ϕ
2,t
t
0 50 100 150
0
50
100
ϕ
3,t
t
0 50 100 150
0
50
100
ϕ
4,t
t
0 50 100 150
0
50
100
ϕ
5,t
t
Figure 2: p = 2, m = 3, a) N
u
= 1, b) N
u
= 2, c) N
u
= 3,
d) N
u
= 4, e) N
u
= 5.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
112

50 100 150
0
50
−50
ϕ
1,t
t
a)
50 100 150
0
50
−50
ϕ
1,t
t
b)
50 100 150
0
50
−50
ϕ
2,t
t
50 100 150
0
50
−50
ϕ
1,t
t
c)
50 100 150
0
50
−50
ϕ
2,t
t
50 100 150
0
50
−50
ϕ
3,t
t
50 100 150
0
50
−50
ϕ
1,t
t
d)
50 100 150
0
50
−50
ϕ
2,t
t
50 100 150
0
50
−50
ϕ
3,t
t
50 100 150
0
50
−50
ϕ
4,t
t
50 100 150
0
50
−50
ϕ
1,t
t
e)
50 100 150
0
50
−50
ϕ
2,t
t
50 100 150
0
50
−50
ϕ
3,t
t
50 100 150
0
50
−50
ϕ
4,t
t
50 100 150
0
50
−50
ϕ
5,t
t
Figure 3: p = 3, m = 2, a) N
u
= 1, b) N
u
= 2, c) N
u
= 3,
d) N
u
= 4, e) N
u
= 5.
50 100 150
0
2
−2
y
1,t
t
50 100 150
0
2
−2
y
2,t
t
50 100 150
0
3
−3
u
1,t
t
50 100 150
0
3
−3
u
2,t
t
Figure 4: p = 2, m = 2, N
u
= 3.
50 100 150
0
2
−2
y
1,t
t
50 100 150
0
2
−2
y
2,t
t
50 100 150
0
3
−3
u
1,t
t
50 100 150
0
3
−3
u
2,t
t
50 100 150
0
3
−3
u
3,t
t
Figure 5: p = 2, m = 3.
50 100 150
0
2
−2
y
1,t
t
50 100 150
0
2
−2
y
2,t
t
50 100 150
0
2
−2
y
3,t
t
50 100 150
0
3
−3
u
1,t
t
50 100 150
0
3
−3
u
2,t
t
Figure 6: p = 3, m = 2.
DIRECTIONAL CHANGE IN A PRIORI ANTI-WINDUP COMPENSATORS VS. PREDICTION HORIZON
113