
DISTURBANCES ESTIMATION FOR MOLD LEVEL CONTROL
IN THE CONTINUOUS CASTING PROCESS
Karim Jabri
1,2
, Bertrand Bele
1
, Alain Mouchette
1
1
Measurement Control Engineering Department, ArcelorMittal Research, Maizières-Lès-Metz, France
Emmanuel Godoy
2
, Didier Dimur
2
2
Department of Automatic Control, Supélec,Gif sur Yvette, France
Keywords: Disturbance estimation, Luenberger observer, Harmonic disturbance, Continuous casting, Mold level
control.
Abstract: This paper addresses the problem of mold level fluctuations in the continuous casting process, which
strongly penalize the quality of the final product and lead to a costly machine downtime. Therefore, the
mold level is controlled using a stopper as the flow control actuator and a level sensor. Under normal
casting conditions, the current controllers provide suitable performances but abnormal conditions require
manual intervention, such as the decrease of the casting speed, in particular when undesired disturbances
like clogging/unclogging or bulging occur. These disturbances increase in severity for certain steel grades or
at high casting speeds. Therefore, this paper focuses on the on-line disturbances estimation in order to
introduce compensation actions. Starting with the presentation of the continuous casting process, the
description of the model of the machine, and highlighting the main control challenges, an observer
estimating clogging and bulging disturbances is then developed. This design may help future control
architectures based on disturbances estimation. The proposed observer is finally validated by extracting
disturbances from experimental signals measured on a continuous casting plant.
1 INTRODUCTION
Nowadays more than 96% of steel is produced by
means of a continuous casting process which has
significantly improved plant productivity in
comparison with other solidification processes.
Accurate control of the molten steel level in the
mold is an important task from both the operating
and quality points of view. Indeed, on the one hand,
it is important to control the mold level to avoid
molten steel overflows or mold emptying. On the
other hand, the mold level must be kept constant to
avoid alumina inclusions and slag being caught up in
the molten steel, leading to defects associated with
cracks in the slabs.
Under normal casting conditions, currently
implemented controllers provide suitable
performances. However, more severe operating
conditions still require manual intervention, such as
the decrease of the casting speed, in particular when
undesired clogging/unclogging or bulging
disturbances occur. These disturbances are in
particular extremely sensitive for certain steel grades
or at high casting speeds. Therefore, on-line
disturbance estimations become an important
challenge with a view to introducing feedforward
actions within the control law.
The paper is structured as follows. Section 2
describes the continuous casting process and the
model of the machine. The design of the observer is
presented in Section 3, successively estimating
clogging, bulging and both disturbances. The
proposed observer is finally validated in Section 4
by estimating disturbances from experimental
signals measured on a continuous casting plant.
119
Jabri K., Bele B., Mouchette A., Godoy E. and Dimur D. (2008).
DISTURBANCES ESTIMATION FOR MOLD LEVEL CONTROL IN THE CONTINUOUS CASTING PROCESS.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 119-124
DOI: 10.5220/0001486601190124
Copyright
c
SciTePress

2 CONTINUOUS CASTING
PLANT MODEL
In the continuous casting process, as shown in
Figure 1, molten steel flows from the tundish into
the mold through the nozzle where it freezes against
water-cooled mold walls to form a solid shell. There
are several rolls below the mold to withdraw the
solidified steel continuously from the bottom of the
mold. The mold has an oscillatory movement with a
magnitude of a few millimetres and a frequency of
about 2 Hz that makes shell extraction easier. At the
outlet of the machine, the steel is fully solidified and
is cut into slabs.
Mold
Nozzle
Stopper
Tundish
Rolls
Solid
Liquid
Actuator
Figure 1: Continuous casting machine.
Usually, the casting speed is kept constant. The
flow out of the mold is thus constant and only the
inflow is controlled.
Figure 2 shows the major components of the
mold level control model without any disturbance
that is usually considered in the plants for the design
of the control law,
-
Mold
out
Q
in
Q
Withdrawal
Sensor
Actuator
Nozzle
P
N
u
+
Figure 2: Plant model.
where
u
is the control input,
P
the stopper
position,
N the mold level,
in
Q and
out
Q the steel
flow-rate into and out of the mold.
This behavioral model shows that the flow into
the mold
in
Q is regulated by the stopper position
P
by acting on the control input u of a hydraulic
actuator. The nozzle is usually modelled in most
cases by a simple gain. The flow out of the mold
out
Q is imposed by the casting speed. The mold
level
N is thus given by the integration of the
difference between
in
Q and
out
Q divided by the
cross section of the mold. This level is measured by
a sensor which can be either an eddy current or a
floating one, returning only local level and not the
whole free surface feature. Transfer functions appea-
ring in the plant model are summarized in Table 1,
Table 1: Transfer functions of the plant model.
Block Transfer function
Actuator
)1(
1
ss
G
a
τ
+
Nozzle
s
G
Withdrawal
vS
Mold
sS
1
Level sensor
s
G
ss
2
1
τ
+
where
s
G is the stopper gain,
ss
G the level sensor
gain,
a
G the actuator gain, S the mold section,
n
τ
the nozzle delay,
1
τ
the actuator time constant,
2
τ
the time constant of the level sensor, v the casting
speed and
s
the Laplace variable.
The control objective is to maintain the mold
level at a specified constant setpoint while limiting
the level fluctuations as much as possible.
Implemented controllers use both the level and
stopper signals as available measurements and
elaborate the actuator input
u acting as the
manipulated variable. Classic control structures
currently working on real plants are of two types: a
first structure considers regulation of the mold level
with a PID controller; a second one includes two
cascaded loops, regulating the stopper position in an
inner loop through a proportional gain and the mold
level in an external loop by means of a PI controller.
However, the control becomes more complex
when disturbances occur on the plant or when the
operating conditions change, leading to an unstable
behavior. In fact, several phenomena disturb the
balance between the flow into and out of the mold,
causing fluctuations over the meniscus surface or an
abrupt increase of the mold level. The standard
controllers are not designed for such casting
conditions. Therefore, new control strategies should
be designed, for example those based on
disturbances rejection. For this purpose, the
disturbances must first be estimated on-line so that
the control structure can compensate their influence
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
120

(Furtmueller and Gruenbacher, 2006). Section 3 will
thus consider the design of observers able to
estimate the two most important disturbances
occurring during continuous casting: the
clogging/unclogging and the bulging.
3 DISTURBANCE ESTIMATION
This Section will successively consider observers for
clogging/unclogging disturbance, then bulging
disturbance and finally for both types.
3.1 Clogging
The clogging event is one of the most serious
phenomena faced by the operators in the continuous
casting machine. It increases operating cost and
decreases productivity. Clogging takes place essen-
tially at the nozzle wall even if in principle it can
occur anywhere inside the nozzle. Nozzle clogging
takes many different forms. The first one is the
sediment of solid inclusions already present in the
steel entering the nozzle. The second form is related
to air aspiration into the nozzle through joints which
leads to reoxidation. The third type of clogging is
attributed to reactions between aluminum in the steel
and an oxygen source in the refractory. In practice, a
given nozzle clog is often a combination of several
of these types (Thomas and Bai, 2001). The
clogging effect is not an instantaneous phenomenon
but develops over time. Its cycle consists of a phase
of slow clogging, followed by a sudden unclogging
that raises considerably the mold level. Its period is
random (Dussud et al., 1998).
This part sets out to propose a clogging
estimation procedure assuming that this is the only
disturbance to arise during the casting operations.
Currently, when the clogging occurs, the controller
forces the stopper to move to maintain a constant
casting speed and a constant level inside the mold.
When the unclogging occurs, the flow passage
inside the nozzle becomes larger. The stopper
position decreases suddenly to reduce the control
zone (opening surface) in order to maintain a
constant flow rate into the mold. During the
clogging/unclogging cycle, the stopper position is
thus a succession of ramps. Therefore, a possible
model of the clogging/unclogging phenomenon can
be the inclusion of an additional flow
clog
d
to
idealin
Q
_
(which is the real inflow without
clogging), as in Figure 3.
clog
d
is also a succession
of ramps because the flow-rate out of the mold
out
Q
and the level
N are generally constant.
clog
d
has
thus the same behavior as the stopper position
P
.
-
+
out
Q
in
Q
Actuator Nozzle
Mold
Sensor
clog
d
-
-
P
N
Withdrawal
+
Figure 3: Plant model taking clogging into account.
The observer is designed considering the stopper
position P and the casting speed v as inputs, and the
mold level N as output. In the following modelling
phase, the time constant of the level sensor is
ignored, since it influences frequencies out of the
bandwidth of the regulation. Without loss of
generality,
ss
G is assumed to be equal to 1.
According to the previous figure:
{
0with
clog
clog
_
=
−−=
d
dvSPGNS
out
idealin
Q
Q
s
&&
321
&
(1)
Thus, the clogging model under the state space
formalism is given by:
⎪
⎩
⎪
⎨
⎧
=
+=
clogclog
logclogclogclogclog
XCN
UBXAX
c
&
(2)
with:
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
clog
clogclog
d
d
N
X
&
,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
v
P
U
clog
,
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
0
0
1
clog
T
C
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−
=
000
100
00
1
clog
S
A ,
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−
=
00
00
1
clog
S
G
s
B
(3)
The observability matrix
clog
O
has full rank 3.
The system is therefore completely observable.
Based on the model Eq. 2, the Luenberger observer
(Sontag, 1998) is given as follows:
NKUB
XCKAX
clogclogclog
clogclogclogclogclog
ˆ
)(
ˆ
++
+−=
&
(4)
where
clog
K is the observer gain chosen so that the
observer is stable and achieves a desired dynamic.
The observer converges if the eigenvalues of the
square matrix
clogclogclog
CKA −
are strictly nega-
tive.
clog
K
is in a first step chosen to satisfy this
condition. The observer is afterwards adjusted with
DISTURBANCES ESTIMATION FOR MOLD LEVEL CONTROL IN THE CONTINUOUS CASTING PROCESS
121

dynamics as fast as possible, the compromise being
that its stability decreases with increasing dynamics.
3.2 Bulging
During the continuous casting process of a slab, the
volume of liquid steel inside the solidified shell can
be changed by strand bulging in the secondary
cooling zone. The bulging occurs between rolls due
to increasing pressure inside the strand. It is divided
into static or dynamic bulging, according to the
strand movement, and steady or unsteady bulging
according to the variation with time (Yoon et al.,
2002). The most disruptive type is the unsteady
bulging generating level fluctuations in the mold.
This part sets out to propose a bulging estimation
procedure assuming that this is the only disturbance
to arise during the casting operations. It is supposed
that the bulging profile at each site between two rolls
is described by a sine function (Lee and Yim, 2000)
with a frequency between 0.05 and 0.15 Hz.
Therefore, this displacement induces changes in the
flow-rate out of the mold. The bulging phenomenon
can thus be modelled by an additional flow
bulge
d
to
idealout
Q
_
(which is the real outflow without
bulging).
bulge
d
is a sum of several sine waves. To
determine its frequencies, the level signal spectrum
must be calculated and the most significant
frequencies belonging to the frequency range
selected. In the following part of this subsection, and
without loss of generality, only two frequencies of
bulge
d
are considered (see Figure 4).
-
Mold
+
out
Q
in
Q
N
Withdrawal
Sensor
Actuator Nozzle
P
idealout
Q
_
+
bulge
d
+
u
Figure 4: Plant model taking bulging into account.
For the following modelling phase, the time
constant of the level sensor is again ignored.
According to Figure 4:
2,1)cos(with
)(
bulge
2bulge1bulge
_
=+=
++−=
itAd
ddvSPGNS
iiii
Q
Q
s
out
idealin
ϕω
44443444421
321
&
(5)
The bulging model under the state space
formalism is thus given by:
⎩
⎨
⎧
=
+=
bulgebulge
bulgebulgebulgebulgebulge
XCN
UBXAX
&
(6)
with
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
2bulge
2bulge
1bulge
1bulge
bulge
d
d
d
d
N
X
&
&
,
⎟
⎠
⎞
⎜
⎝
⎛
=
v
P
U
bulge
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
−−
=
0000
10000
0000
00100
000
2
2
2
1
11
bulge
ω
ω
SS
A
,
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
=
00
00
00
00
1
bulge
S
G
s
B
,
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
0
0
0
0
1
bulge
T
C
(7)
The observability
bulge
O has full rank 5. The
system is thus completely observable. Based on the
model Eq. 6, the Luenberger observer is given by the
following equation:
NKUB
XCKAX
bulgebulgebulge
bulgebulgebulgebulgebulge
ˆ
)(
ˆ
++
+−=
&
(8)
where
bulge
K
is the observer gain adjusted as in
Section 3.1.
3.3 Clogging and Bulging
The previous clogging and bulging observers were
designed separately to estimate respectively
clogging or bulging being the only disturbance
acting on the system. However, when clogging and
bulging occur simultaneously during the continuous
casting operation, these two observers must be
merged into a single global one that will be able to
estimate
clog
d
and
bulge
d
individually (Figure 5).
-
+
out
Q
in
Q
Actuator Nozzle
Mold
Sensor
clog
d
-
-
P
N
Withdrawal
+
bulge
d
Figure 5: Plant model with clogging and bulging effects.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
122

With this figure, merging Eqs. 1 and 5 leads to:
2,1)cos(
0with
)(
bulge
2bulge1bulgebulge
clog
bulgeclog
=+=
+=
=
+−−=
itAd
ddd
d
dvSdPGNS
iiii
QQ
s
outin
ϕω
&&
44344214434421
&
(9)
which results in the global clogging/bulging model
under the state space formalism:
⎪
⎩
⎪
⎨
⎧
=
+=
estest
estestestestest
XCN
UBXAX
&
(10)
with:
(
)
bulge2bulge2bulge1
bulge1clogclog
ddd
dddNX
T
est
&&
&
=
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
−−−
=
000000
1000000
000000
0010000
0000000
0000100
0000
2
2
2
1
111
ω
ω
SSS
est
A
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
v
P
U
est
,
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
=
00
00
00
00
00
00
1
S
G
est
s
B
,
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
0
0
0
0
0
0
1
T
est
C
(11)
The observability matrix
est
O has full rank 7.
The system is thus completely observable. Based on
the model Eq. 10, the global Luenberger observer is
given by the following equation, where
est
K is the
observer gain adjusted as previously:
NKUB
XCKAX
estestest
estestestestest
++
+−=
ˆ
)(
ˆ
&
(12)
The generalization to more than two frequencies
taken into account in the bulging disturbance is
performed by considering two additional state
variables per added frequency, with adequate rows
and columns in the state representation. It must be
noticed that, due to the observer structure, the ave-
rage of the
bulge
d signal is included in the estima-
tion of
clog
d . In short,
clog
d contains the average
of
bulge
d and a succession of ramps possibly.
4 OBSERVER VALIDATION
The previous global observer is now applied on
experimental data registered during continuous
casting operations. A first experiment is considered
(record 1), for which the eigenvalues of the observer
have been tuned (according to bulging signal
frequencies) to −1.5, −1.57, −1.27, −1.42, −1.35,
−1.2 and −1.12. Results are given in Figures 6 and 7.
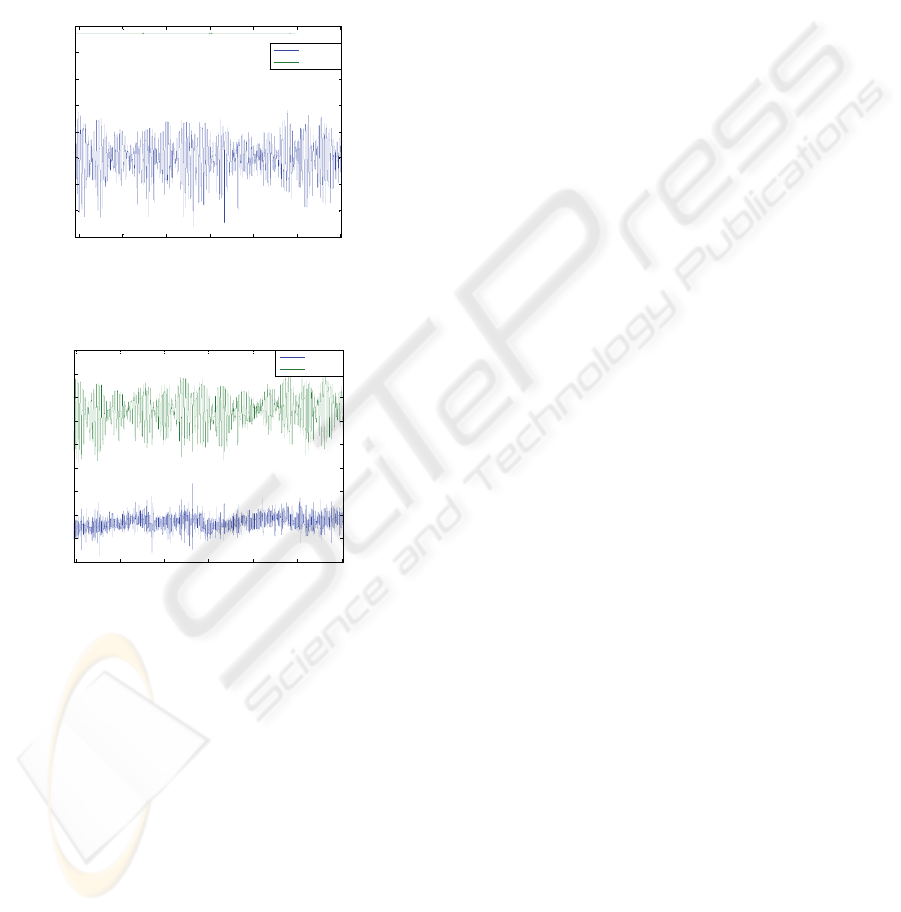
Figure 6 compares the estimated
bulge
d
to
idealout
Q
_
.
idealout
Q
_
appears to be ten times
greater than
bulge
d
. It can be concluded that there is
no bulging effect in this first record.
0 500 1000 1500
-10
-5
0
5
10
15
20
Flow out (l/s)
d-bulge
Qout-ideal
Figure 6: Comparison between the estimated
bulge
d and
idealout
Q
_
in the case of the first record.
0 500 1000 1500
5
10
15
20
25
30
35
40
Flow (l/s)
Qin-ideal
d-clog
Qin
Figure 7: Comparison between the estimated
clog
d , the
ideal and the real input into the mold for the first record.
Knowing this, Figure 7 now compares the
estimated
clog
d elaborated by the observer with the
ideal (
idealin
Q
_
) and the real (
in
Q ) input into the
mold in the case of this first record.
idealin
Q
_
is
recomputed by means of the measurement of the
stopper position
P
as mentioned in Eq. 5 and
in
Q
is recalculated by means of the relation in Eq. 9. It is
shown that the estimated clogging disturbance
follows the expected profile, i.e. ramp variations
during the clogging phase and a sudden decrease due
to unclogging. This figure also illustrates that
in
Q is
three times smaller than the ideal value
idealin
Q
_
Time (s)
Time (s)
DISTURBANCES ESTIMATION FOR MOLD LEVEL CONTROL IN THE CONTINUOUS CASTING PROCESS
123
expected without clogging. Thus this estimation by
means of an observer, which may be useful for
control purposes, also helps to quantify the intensity
of the clogging phenomenon.
The observer, tuned as previously, is now
applied to a second experiment (record 2). In this
case, three frequencies of the signal
bulge
d
have to
be considered, respectively 0.084, 0.095 and
0.082 Hz as the most significant in the bulging
frequency range [0.05, 0.15] Hz.
400 600 800 1000 1200 1400 1600
-6
-4
-2
0
2
4
6
8
10
Flow out (l/s)
d-bulge
Qout-ideal
Figure 8: Comparison between the estimate
bulge
d and
idealout
Q
_
in the case of the second record.
400 600 800 1000 1200 1400 1600
10
12
14
16
18
20
22
24
26
28
Flow in (l/s)
d-clog
Qin-ideal
Figure 9: Comparison between the estimated
clog
d and
idealin
Q
_
in the case of the second record.
Figures 8 and 9 show the estimated disturbances
bulge
d and
clog
d . Figure 9 compares the estimation
of
clog
d to
idealin
Q
_
. Without ramp in
clog
d , it can
be concluded that
clog
d only represents the average
of the
bulge
d signal of Figure 8 which should be
added to it in order to estimate its correct value, and
that there is no clogging effect in this record. From a
control point of view as described in (Furtmueller
et
al
., 2005), to have the average of
bulge
d included in
clog
d is not problematic. In fact, the control
structure which compensates disturbances should
use the sum of
clog
d and
bulge
d as an input and not
the two disturbance estimations separately.
5 CONCLUSIONS
This paper presents the elaboration of a global
observer designed to estimate clogging and bulging
disturbances appearing in a continuous casting
process. These estimations may be further used as
inputs to compensation modules within mold level
control structures. This observer is built with
behavioral models of the physical process, assuming
that these disturbances can be modelled as
exogenous signals. Further research may consider a
nonlinear nozzle gain to model the clogging effect,
robustness analysis of the estimator, particularly
with respect to variations of the bulging signal
frequencies and model uncertainties.
REFERENCES
Thomas, B.G., Bai, H., 2001. Tundish nozzle clogging –
application of computational models. In
18
rd
PTD
Conf. Proc.
, Baltimore (US).
Sontag, E., 1998.
Mathematical Control Theory:
Deterministic Finite Dimensional Systems
, Springer.
2
nd
edition.
Yoon, U-S., Bang, I.-W., Rhee, J.H., Kim, S.-Y., Lee, J.-
D., Oh, K.H., 2002. Analysis of mold level hunching
by unsteady bulging during thin slab casting. ISIJ
International, 42(10):1103-1111.
Lee, J.D., Yim, C.H., 2000. The mechanism of unsteady
bulging and its analysis with the finite element method
for continuously cast steel. ISIJ International,
40(8):765-770.
Dussud, M., Galichet, S., Foulloy L.P., 1998. Application
of fuzzy logic control for continuous casting mold
level control.
IEEE Transactions on Control Systems
Technology
, 6(2).
Furtmueller, C., Gruenbacher, E., 2006. Suppression of
periodic disturbances in continuous casting using an
internal model predictor. In
Proc. IEEE Intl. Conf. on
Control Applications
, Munich, Germany.
Furtmueller, C., Del Re, L., Bramerdorfer, H., Moerwald,
K., 2005. Periodic disturbance suppression in a steel
plant with unstable internal feedback and delay. In
Proc. 5
th
Intl. Conf. on Tech. and Automation, Greece.
Time (s)
Time (s)
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
124
