COLLISION AVOIDANCE SYSTEM PRORETA

Strategies Trajectory Control and Test Drives

R. Isermann, U. Stählin and M. Schorn

Institute of Automatic Control, Technische Universität Darmstadt

Landgraf-Georg-Str. 4, 64283 Darmstadt, Germany

Keywords: Collision avoidance, vehicle, object detection, path following, automatic braking, automatic steering.

Abstract: Methods and experimental results of a collision avoidance driver assistance system are described with

automatic object detection, trajectory prediction, and path following with controlled braking and steering.

The objects are detected by a fusion of LIDAR scanning and video camera pictures resulting in the location,

size and speed of objects in front of the car. A desired trajectory is calculated depending on the distance, the

width of a swerving action and difference speed. For the trajectory control different control methods were

designed and tested experimentally like velocity depend linear feedback and feedforward control, nonlinear

asymptotic output tracking and nonlinear flatness based control using extended one-track models with

vehicle state estimation for the sideslip angle and cornering stiffness. Automatic braking is realized with an

electrohydraulic brake (EHB) and automatic steering with an active front steering (AFS). The various

control systems are compared by simulations and real test drives showing the behaviour of a VW Golf with

automatic braking or/and automatic swerving to a free track, such avoiding hitting a suddenly appearing

obstacle. The research project PRORETA was a four-years-cooperation between Continental Automotive

Systems and Darmstadt University of Technology.

1 INTRODUCTION

Driver Assistance Systems for Collision Avoidance

have the goal to prevent accidents using braking or

evasive maneuvers. An automatic collision

avoidance system has to monitor its surroundings,

detect an upcoming accident and intervene

appropriately to avoid the accident. In case of the

system developed by the research project

PRORETA – Electronic Driver Assistance System

for a Collision Avoiding Vehicle, a cooperation

between Technische Universität Darmstadt and

Continental AG, the driver is given the chance to

avoid the accident himself as long as possible.

Therefore, the interventions have to be conducted at

the physical last possible moment or the driving

dynamics stability boundary.

Using these predictions, a decision is made,

whether an intervention is necessary or not and the

intervention is planned. The intervention itself is

then conducted fully automatically. An ergonomic

study accompanied the development of the system.

This study investigated how the driver reacts in

critical situations and how he reacts on the

interventions by PRORETA.

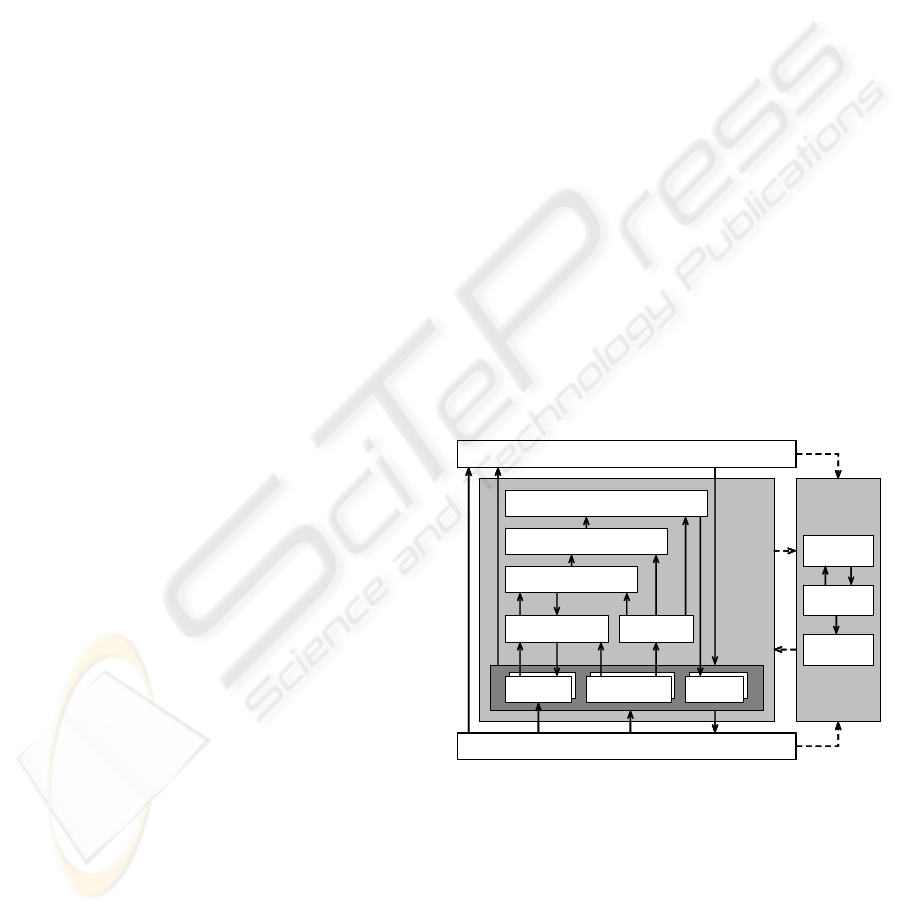
Environment

Driver

Control

Sensors for

vehicle states

Vehicle state

estimation

Intervention planning

Environmental

sensors

Fusion of environmental

sensors and state estimation

for the environment

Trajectory prediction

PRORETA

prototype

Vehicle

Actuators

Experiments

with test persons

Analysis

Ergonomic

studies

Reactions of drivers,

design notes,

acceptance

Environment

Driver

Control

Sensors for

vehicle states

Vehicle state

estimation

Intervention planning

Environmental

sensors

Fusion of environmental

sensors and state estimation

for the environment

Trajectory prediction

PRORETA

prototype

Vehicle

Actuators

Experiments

with test persons

Analysis

Ergonomic

studies

Reactions of drivers,

design notes,

acceptance

Figure 1: System overview prorate.

In this contribution, the intervention decision, the

planning of the intervention and the conduction of

the intervention are described. The environment

perception is described in detail in (Darms and

Winner, 2006). Results from the ergonomic study

can be found in (Bender and Landau, K., 2006). The

system was tested using a complex two track model

followed by extensive driving tests with an

experimental vehicle.

Isermann R., Stählin U. and Schorn M. (2008).

COLLISION AVOIDANCE SYSTEM PRORETA - Strategies Trajectory Control and Test Drives.

In Proceedings of the Fifth Inter national Conference on Informatics in Control, Automation and Robotics - ICSO, pages 35-42

DOI: 10.5220/0001489300350042

 SciTePress

2 TEST VEHICLE

A VW Golf IV, which was only equipped with

additional sensors and actuators required for the

developed functions, served as experimental vehicle,

see Figure 2.

Figure 2: Environmental Sensors of the test vehicle.

The driver assistance system uses an active front

steering and an electro hydraulic braking system as

actuators. For vehicle state estimation only ESP

sensors and the sensors of the active front steering

and braking system are necessary. For environment

perception a laser scanner and a video sensor were

used. The chosen design allows to scan the area in

front of the vehicle. The detection area of the laser

scanner covers an angular range of 22.5° with a

resolution of 1.5° and is scanned in a 90 ms cycle.

The distance to objects is determined by a time of

flight measurement of emitted light impulses. The

video sensor is based on a monochrome CMOS

image sensor that provides data in a 40 ms cycle.

The detection area is 44°, whereas the discretisation

with approx. 0.07° is considerably finer than for the

laser scanner. By means of image processing

algorithms, vehicle rear views and lane markings

can be detected in the image, however, a direct

distance measurement is not possible, for details see

(Darms and Winner, 2006).

3 EVASIVE TRAJECTORY

An evasive trajectory is required between

intervention planning and control For investigating

several different intervention functions with

different types of controllers, the type of

intervention is selected using some flags. The flags

used in this article are braking, emergency braking

and evasion. If braking is chosen, the desired

deceleration has to be transmitted. If an emergency

braking is chosen, the maximum possible

deceleration at every point in time is achieved using

braking controllers. For an evasion, the desired

position and heading are given for one time step T

two time steps T

and ten time steps T

ahead in

time, Figure 3. The coordinate system used is

stationary for the duration of the evasion and is

initialized at the beginning of the evasion to match

the vehicle coordinate system at that point. The last

position, which is supposed to be reached 10 time

steps in the future, is used to make sure the

controller can react predictively on deviations of the

first 2 time steps. Figure 3 shows this interface.

Every point p(t) consists of the position (x, y) and

the heading

of the vehicle. All three points are put

together in one matrix transmitted to the controller:

(

)

(

)

(

)

210

evasion

pt T pt T pt T

⎡

⎤

=+ + +

⎢

⎥

⎣

⎦

Figure 3: Evasive trajectory between planning and control.

4 PLANNING OF THE EVASIVE

INTERVENTION

Primary goal of the evasive trajectory is to reach a

predefined lateral offset with the shortest possible

traveled path. The designed trajectory has to be

feasible regarding the vehicle dynamics laws and

after the maneuver the vehicle has to be in a safe and

stable state.

Vehicle dynamics laws of the trajectory are

taken into account to limit the maximum allowed

lateral acceleration. This limit can be adapted to the

actual traffic and driving situation, especially

weather conditions. The steering actuator also limits

the maximum possible jerk.

Since the trajectory is transmitted to the

controller using positions, the general relations

between the position on the trajectory and the

driving dynamics are considered first. This relation

is based on the simple equations of the one-track

model and the Ackermann equations. The approach

shown here uses a relation where the y-position on

the trajectory is depended on the x-position:

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

()yfx=

(1)

Using geometric transformations, the yaw angle

can be expressed as (assuming no side slip)

arctan

⎛⎞

⎜⎟

⎝⎠

(2)

and therefore its derivative regarding time yields:

ddy

dt dx

⎛⎞

⎜⎟

⎝⎠

(3)

Based on this and using the Ackermann relations,

the lateral acceleration is:

av vv

⎛⎞

⎜⎟

⎝⎠

(4)

Further simplification can be accomplished

assuming

= .

Often, a sequence of klothoids is used for the

evasive trajectory, see e.g. (Ameling, 2002). In

general, trajectories for evasive maneuvers have the

shape of a lying S. Functions describing such a

shape are called sigmoidal functions or sigmoides.

In the following a sigmoide of the form

()

ax c

−−

(5)

is used. B is the maneuver width, describing the

distance between minimum and maximum y-value. a

defines the slope of the sigmoide, where high values

for a are leading to a steeper curve. c defines the

position of the inflection point and therefore the

length of the evasive maneuver, which is s=2c.

Looking at equation (5), the sigmoide has its

maximum and minimum at infinity, meaning

lim ( ) 0

→−∞

(6)

and

lim ( )

yx B

→∞

(7)

respectively. Therefore, an additional parameter

Tol

y is introduced. Using this parameter, the

following counts:

Tol

(0)yy=

(8)

and

Tol

(2 )yc By=−

(9)

Figure 4 shows this sigmoide and the respective

parameters. The parameters can be chosen according

to the driving situation, such that the evasive path is

minimal regarding the limitations for maximum

lateral acceleration, maximal jerk and dynamics of

the steering actuator. The derivation of the

respective parameters can be found in (Stählin et al.,

2006).

Figure 4: Evasive sigmoide and its parameters.

The most important value for taking a decision,

whether the klothoide or the sigmoide should be

chosen for the evasive trajectory is the length s of

the path of the evasive maneuver, taking into

account the limiting factors (maximum lateral

acceleration, maximum jerk,…). Table 1 shows a

comparison between klothoide and sigmoide for

different limiting factors. It can be seen, that the

sigmoide always leads to a shorter path for the

evasive maneuver. This is due to the linear increase

of the lateral acceleration for the klothoide in

comparison to the faster and nonlinear increase in

lateral acceleration for the sigmoide. Both

trajectories can be realized by a controller trajectory.

Table 1: Comparison of the length of an evasion for

klothoide and sigmoide with y

B v lateral

accel.

jerk Klothoide Sigmoide

2m 15m/s 5m/s2 30m/s3 26,83m 22,08m

3m 15m/s 5m/s2 30m/s3 32,85m 29,10m

2m 36m/s 5m/s2 30m/s3 64,30m 53,39m

3m 36m/s 5m/s2 30m/s3 78,85m 70,42m

5 INTERVENTION DECISION

Based on the fused environment data it is decided if

a collision is likely to occur and if so, which

maneuver has to be carried out to avoid the collision.

The strategy is to avoid the collision at the

physically last possible moment by an intervention

in order to give the driver the possibility to defuse

the critical situation by his own actions as long as

possible.

In order to determine a threatening collision,

predictions are first made for the own vehicle

driving tube and the movement of the objects in the

environment. By means of these predictions it can

then be predicted whether a collision will occur. If

this is the case, it is planned in a next step when and

which intervention has to be carried out.

COLLISION AVOIDANCE SYSTEM PRORETA - Strategies Trajectory Control and Test Drives

Basically, there are three strategies to avoid a

collision:

 Braking

 Steering

 Combination of braking and steering

For the intervention decision it is calculated at what

distance to the collision location the respective

intervention has to be carried out, such that the

collision can still be prevented. For a braking

intervention the braking distance is calculated. In

case of steering interventions the sigmoide is taken

as the basis for the evasive trajectory.

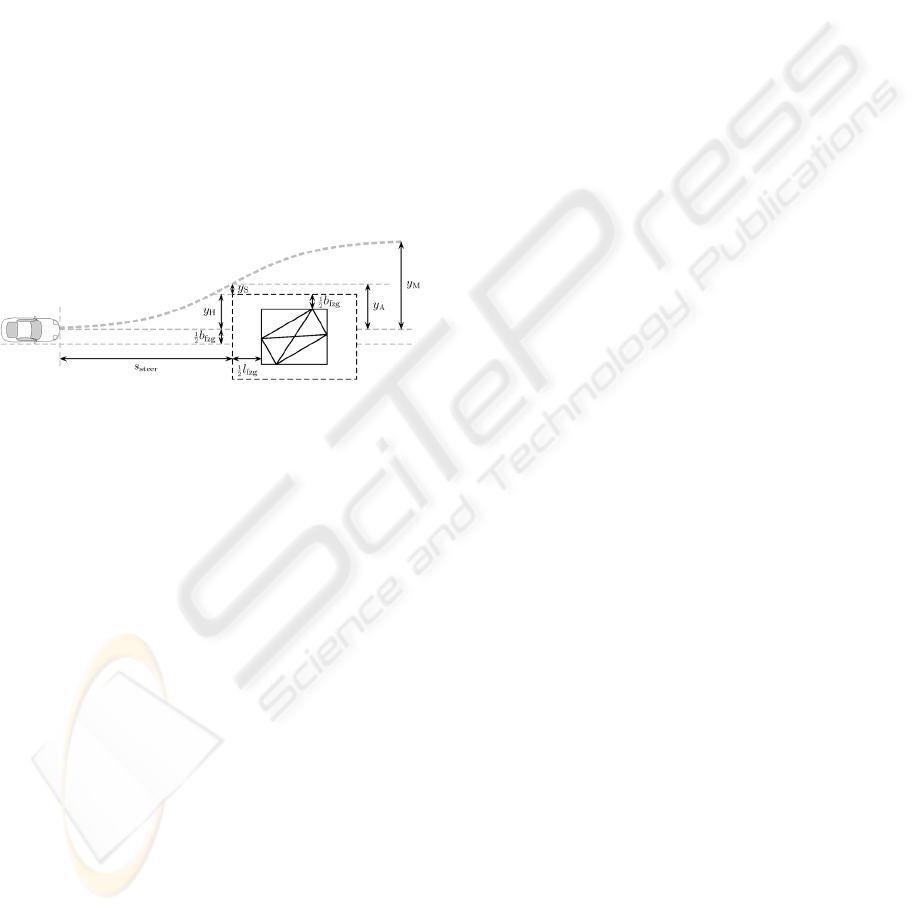
In Figure 5 the quantities necessary for the

calculation of the evasive trajectory are presented.

By means of the vehicle’s width b

and the

obstacle’s width the necessary evasive width y

determined together with a safety distance y

. Since

the evasive width can be reached before the end of

the maneuver, an associated maneuver width y

arises.

Figure 5: Evasive Quantities for calculating the evasive

trajectory (see text for details).

However, the evasive trajectory is the trajectory

until the evasive width y

is reached. The maneuver

width is chosen according to the strategy used. If the

maneuver width y

is chosen to be the same as the

evasive width y

, the evasive trajectory length s

steer

reaches its maximum for given maximal lateral

acceleration and maximal lateral jerk. These two

last-named parameters also determine the optimal

maneuver width which leads to the smallest possible

evasive trajectory length s

steer

and which makes use

of the set limits ideally. However, it needs

considerably more lateral offset for the same evasive

width y

6 LATERAL VEHICLE

GUIDANCE

If a collision with an obstacle is no longer avoidable

by a reaction of the driver, then, according to the

situation, the driver assistance system selects one of

the intervention strategies described above. For the

realization of the chosen intervention either the

active steering and/or the electro hydraulic braking

system are used according to the maneuver. If a

braking maneuver should be carried out, the vehicle

is decelerated (Schorn et al., 2005) by utilization of

the maximum force transmission available. The anti-

lock braking system ABS supports in this case.

In case a collision can only be prevented by an

evasive maneuver or by a combined evasive and

braking maneuver the control block receives from

intervention planning a trajectory, see Figure 1. The

vehicle is driven on this trajectory automatically

around the obstacle. Different linear and nonlinear

feedback controllers for an evasive maneuver were

developed, see e.g. (Schorn and Isermann, 2006),

(Schorn et al., 2006). Each lateral guidance feedback

control transfers an additional steering angle to the

interface of the steering system. Vehicle variables,

which cannot be measured directly by sensors the

vehicle is equipped with, are estimated, see Figure 1,

see also (Schorn and Isermann, 2006), (Isermann,

2006). For combined steering and braking

maneuvers different feedback controllers were

developed as well.

In the following only the lateral vehicle guidance

is regarded. Exemplarily, two of the investigated

approaches, a nonlinear asymptotic output tracking

feedback control and a speed-dependent local linear

feedback control approach with feedforward control

are presented.

6.1 Nonlinear Asymptotic Output

Tracking Feedback Control

For model based design of a feedback system, the

system behavior is required. The path following

feedback control is based on an extended one-track

model:

()

1111122

2211222

331 14

sin

xaxax

xa xx

⋅+ ⋅

⎡⎤⎡ ⎤

⎡⎤

⎢⎥⎢ ⎥

⎢⎥

⋅+ ⋅

⎢⎥⎢ ⎥

⎢⎥

+⋅

⎢⎥⎢ ⎥

⎢⎥

⋅+

⎢⎥⎢ ⎥

⎢⎥

⎢⎥⎢ ⎥

⎣⎦

⎣⎦⎣ ⎦

(10)

[

]

0010

=⋅=x

(11)

with

()

and (t)

()

⎡⎤

⎢⎥

== =

⎢⎥

⎣⎦

(12)

is the sideslip angle,

the yaw angle, y

the

lateral vehicle position and

the steer angle. The

speed dependent parameters follow from front and

rear cornering stiffness c

and c

, length from

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

front and rear axle to the center of gravity l

and l

velocity v, mass m and moment of inertia J

, see

e.g., (Isermann, 2006):

FR RRFF

11 12

RRFF RRFF

21 22

FFF

11 21

cc lclc

mv mv

lc lc lc lc

JJv

ccl

mv J

αα α α

αα

+⋅−⋅

=− = −

⋅⋅

⋅−⋅ ⋅+⋅

==−

⋅

(13)

The model parameters were determined from

construction data and identification experiments,

(Schorn, 2007).

The lateral position y

(t)=f(x

(t)) of the vehicle

in an earth-fixed coordinate system has to be

controlled using the evasive trajectory described by

equation (5). The reference input of the control

system y

(t) is calculated by performing an

interpolation.

The vehicle model in (10) and (11) is a nonlinear

single-input single-output model of type:

() ( ) ( ) ()

( ) ( ( )) with ( )

tut

tt t

=+⋅

xaxbx

ycx xx

(14)

Having the system's output

y(t) converging

asymptotically to a prescribed reference output y

(t),

the system input u(t) can be calculated as follows

(Isidori, 1989), (Schwarz, 1999):

() 1 (1)

R1 R

()

LL ( )

L() () L () ()

dd i i

cyt cyt

−

−−

−

=⋅

⎡⎤

−+−⋅ −

⎡

⎤

∑

⎣

⎦

⎢⎥

⎣⎦

(15)

The relative degree d has to be determined according

to (Isidori, 1989), (Schwarz, 1999). For the

mentioned plant it yields d = 2 assuming v > 0 and

()

,...

ττ

±±≠+ xx . With this information, the

feedback control, equation (15), can be calculated.

The elements are given by (Schorn et al., 2006):

()

()( )

()

14 1111222

11 1 4

()

L() sin

L() cos

LL ( ) cos

cvxx

cvxxaxaxx

cbv xx

=⋅ +

=− ⋅ + ⋅ + +

=⋅⋅ +

(16)

where L

are so called Lie-functions (Isidori, 1989),

(Schwarz, 1999). The structure of the resulting

closed control loop is shown in Figure 6. The

command variables, the reference output y

(t),

(),

()

as described above, are calculated in

the component “Calculation of command variables”.

The sideslip angle was estimated with a vehicle state

estimator (Schorn and Isermann, 2006). The output

of the controller is an additional steering

angle

)()(

= .

Results from test drives with the experimental

vehicle described above will be presented below.

Figure 6: Structure of nonlinear asymptotic output

tracking feedback control.

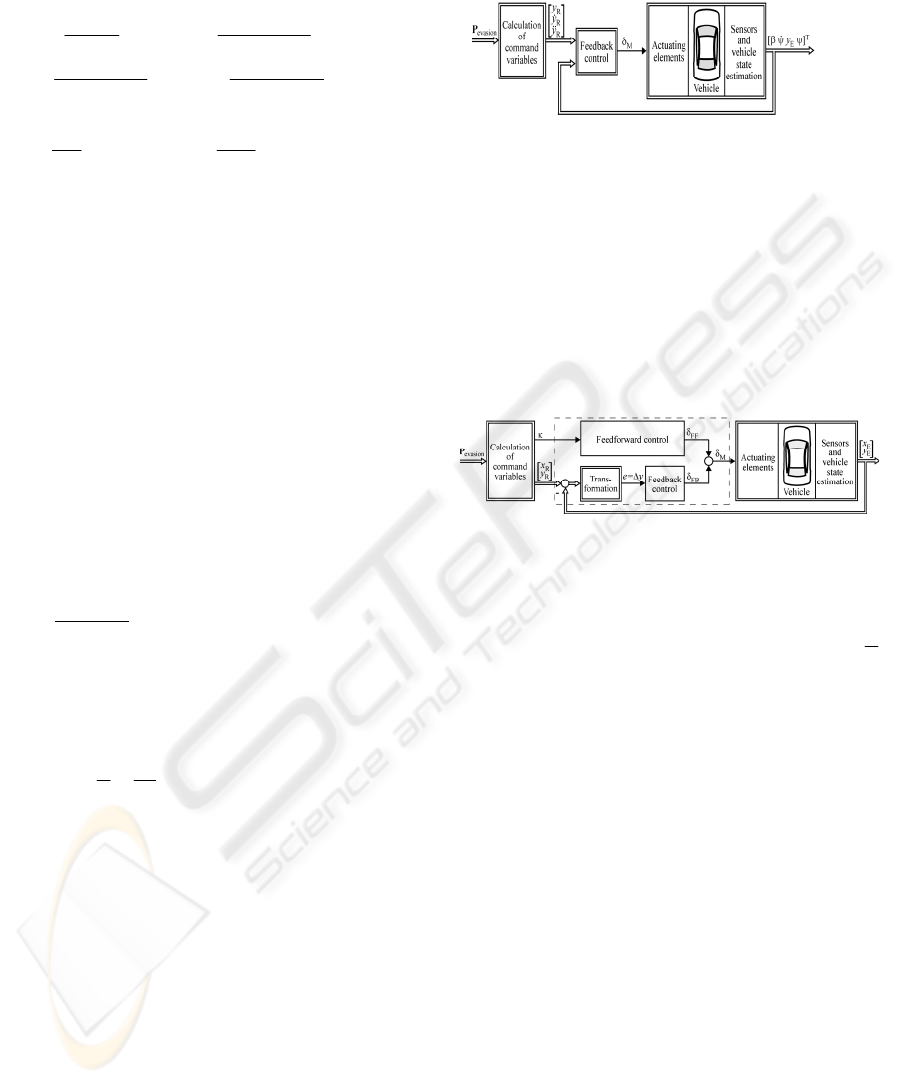
6.2 Speed-dependent Local Linear

Feedback Control with

Feedforward Control

To guide a vehicle on a desired trajectory, a speed-

dependent local linear feedback control approach

with feedforward control was developed (Schorn

and Isermann, 2006). A scheme of the control

system is shown in Figure 7.

Figure 7: Structure of linear feedback control combined

with feedforward action.

Based on the self steer gradient SG a steer angle

is calculated for the feedforward control by means of

vehicle velocity v, wheelbase l and curvature

of the desired trajectory:

(

)

lSGv

+⋅⋅

(17)

A feedback control is added to compensate

disturbances and deviations. The parameters of a

proportional-derivative (PD) controller is tuned by

two parameters only and provides the required

dynamics by means of the differential component.

Using the vehicle orientation

, the control

deviation is transformed from an earth-fixed

coordinate system into a vehicle-fixed coordinate

system as control deviation e=

y. The feedback of

the vehicle’s longitudinal position

is necessary

for this purpose. The steering system is driven by the

sum

of the angles

and

of the feedforward

and feedback control. For the implementation of the

feedback control in the experimental vehicle the

derivative, required for the calculation of the

differential component of the control variable, was

replaced by a high pass filter.

As the velocity v influences the vehicle’s

dynamics, because it changes continuously during a

COLLISION AVOIDANCE SYSTEM PRORETA - Strategies Trajectory Control and Test Drives

driving cycle. The feedback controllers were

designed for different operating points (velocities).

Their outputs are weighted and superimposed based

on Local Linear Models (LLM) (Schorn and

Isermann, 2006), (Nelles, 2001).

7 EXPERIMENTAL RESULTS

FROM TEST DRIVES

The developed components environment

recognition, intervention decision and feedback

control were implemented as a whole system in a

test vehicle and tested by means of numerous

experiments. This happened using an obstacle that

represents the rear view of a car and can be moved

laterally on the lane. Two test scenarios can be seen

in Figure 8.

In the following sections the most important

results from these tests are presented. It is required

in each case that the lateral and back lane areas are

monitored by additional sensors and thus permit

driving maneuvers.

Figure 8: Scenarios for practice system testing.

7.1 Blocked Lane

In the scenario "Suddenly appearing obstacle /

blocked lane" from Figure 8a) a lane is blocked

unexpectedly. An example for this would be an end

of a traffic jam in the case of bad visibility or after a

curve. The emergency evasion is then conducted as

an automatic intervention. The position of the used

obstacle is determined by the environmental sensors

and the necessary evasive trajectory is calculated

based on the information about the vehicle’s

surroundings. The vehicle is then guided aside of the

obstacle on the predefined evasive trajectory by the

lateral guidance controller without the assistance of

the driver.

Figure 9 shows results of a test drive with the

test vehicle mentioned above, where the asymptotic

nonlinear output tracking feedback control was

used. A comparison of desired command variable

and measured position shows that both values match

very well. The evasive width y

is 3m, the desired

and the actual position correspond well, apart from a

slight overshooting. The steering wheel angle

indicates that the driver held the steering wheel in a

straight position. The difference between total angle

and steering wheel angle is provided only by the

controller. The difference at the end of the

intervention maneuver follows from the fact that the

feedback control has been switched off at very low

velocities.

Results from test drives for the linear feedback

control combined with feedforward are presented in

Figure 10.

Again, desired command variable and measured

position match very well. The general conditions for

this test drive have been the same as for the results

shown in Figure 9 regarding evasive width y

and

velocity. The experiments show that the maximal

lateral accelerations are

a ≈

and the linear

controller needs less maximal steering angle. Both

control approaches presented above provide similar

accuracies, but the speed dependent linear control

system can be implemented and parameterized

easier and with smaller computational expense.

7.2 Cutting-in Vehicle

As a second scenario a suddenly cutting-in vehicle is

reproduced by moving the dummy obstacle just in

front of the vehicle from the right to the left lane

(Figure 8b). Evasion is not possible since further

obstacles block the right. The necessary maneuver is

thus an emergency braking maneuver. By means of

the environmental sensors it is recognized that both

lanes of the road are blocked and it is calculated at

which last possible moment the emergency braking

maneuver must be started in order to come to a stop

just before the obstacle. Assuming a maximum

braking acceleration which is dependent on the road

state (dry-wet), the required braking distance of the

vehicle is calculated depending on the current speed.

The driver assistance system triggers a braking

intervention only if this minimal braking distance is

reached in order to give the driver the chance to

prevent the collision as long as possible by himself.

The electro hydraulic braking system then

decelerates the vehicle maximally with support by

the anti-lock braking system ABS, on dry roads with

a deceleration of

a ≈

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

Figure 9: Results for asymptotic nonlinear output tracking feedback (test drive).

Figure 10: Results for linear feedback control combined with feedforward (test drive).

8 CONCLUSIONS

The described system for accident avoidance which

was developed within the scope of the project

PRORETA was presented to an audience selected by

Continental Teves and TU Darmstadt. The guests

had the possibility of experiencing the system within

the scope of driving experiments. Every guest drove,

amongst others, the scenarios presented in Figure 8.

The system worked robustly and faultlessly.

However, until such a system is available on the

market, some tasks have still to be solved. An

important one is the analysis of the oncoming traffic

which is examined in a subsequent PRORETA

project.

ACKNOWLEDGEMENTS

The authors highly appreciate the financial support

for the PRORETA project and good cooperation

with Continental Automotive Systems and the

support especially by Dr. R. Rieth, J. Diebold, M.

Arbitmann, Dr. S. Lüke, B. Schmittner. We also

COLLISION AVOIDANCE SYSTEM PRORETA - Strategies Trajectory Control and Test Drives

would like to thank our colleagues within the

PRORETA Team, Eva Bender and Michael Darms

with Prof. Winner, Prof. Landau and Prof. Bruder

for the excellent cooperation. Their results are

published e.g. in (Darms and Winner, 2006),

(Bender et al., 2006).

REFERENCES

Ameling, C., 2002. Steigerung der aktiven Sicherheit von

Kraftfahrzeugen durch ein Kollisionsvermeidungs-

system. VDI Verlag, Düsseldorf.

Bender, E., Darms, M., Schorn, M., Stählin, U., Isermann,

R., Winner, H., Landau, K.. 2007, Anti collision

system PRORETA - on the way to the collision

avoiding vehicle. Part 1: Basics of the System & Part

2: Results. ATZ (Automobiltechnische Zeitschrift,

English Supplement) 109 (4 & 5) 336-341 & 456-463.

Bender, E., Landau, K., 2006. Fahrerverhalten bei

automatischen Brems- und Lenkeingriffen eines

Fahrerassistenzsystems zur Unfallvermeidung, VDI-

Bericht 1931, AUTOREG 2006, Wiesloch.

Bender, E.; Landau, K., Bruder, R., 2006. Driver reactions

in response to automatic obstacle avoiding

manoeuvres. In: IEA 2006 – 16th World Congress on

Ergonomics, July 10-14, 2006, Maastricht, the

Netherlands.

Darms, M., 2007. Eine Basis-Systemarchitektur zur

Sensordatenfusion von Umfeldsensoren für

Fahreassistenzsysteme. Dissertation. Fortschr.-Ber.

Reihe 12, No. 653. VDI-Verlag, Düsseldorf.

Darms, M., Winner, H., 2006. Umfelderfassung für ein

Fahrerassistenzsystem zur Unfallvermeidung, VDI

Bericht 1931, AUTOREG 2006, Wiesloch.

Isermann, R., 1989. Digital control systems. Springer-

Verlag, Berlin and New York.

Isermann, R. (ed), 2006. Fahrdynamik-Regelung,

ATZ/MTZ-Fachbuch, Vieweg, Wiesbaden.

Isidori, A., 1989. Nonlinear Control Systems – An

Introduction. Springer-Verlag. Berlin.

Nelles, O., 2001. Nonlinear System Identification.

Springer-Verlag. Berlin.

Schorn, M., 2007. Quer- und Längsregelung eines

Personenkraftwagens für ein Fahrerassistenzsystem zu

Unfallvermeidung. Dissertation. Fortschr.-Ber. VDI

Reihe 12, no 651. VDI Verlag, Düsseldorf.

Schorn, M., Schmitt, J., Stählin, U., Isermann, R., 2005.

Model-based braking control with support by active

steering. In: 16th IFAC World Congress, July 4-8,

2005, Prague, Czech Republic.

Schorn, M., Isermann, R., 2006. Automatic Steering and

Braking for a Collision Avoiding Vehicle. 4th IFAC-

Symposium on Mechatronic Systems, September 12-

14, Wiesloch / Heidelberg.

Schorn, M., Stählin, U., Khanafer, A., Isermann, R., 2006.

Nonlinear Trajectory Following Control for Automatic

Steering of a Collision Avoiding Vehicle. American

Control Conference, June 14-16, Minneapolis,

Minnesota, USA.

Schwarz, H., 1999. Einführung in die Systemtheorie

nichtlinearer Regelungen. Shaker Verlag. Aachen.

Stählin, U., Schorn, M., Isermann, R., 2006.

Notausweichen für ein Fahrerassistenzsystem zur

Unfallvermeidung, VDI Bericht 1931, AUTOREG

2006, Wiesloch.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics