POSITION CONTROL METHOD OF A NON-CONTACTING
CONVEYANCE SYSTEM FOR STEEL STRIP
Yeongseob Kueon, Hyoung Jin Yoon
+
Process Control and Rolling Technology Research Gr., POSCO Tech. Res. Lab., S. Korea
Yoon Su Baek
+
+
Department of Mechanical Engineering , Yonsei University, Seoul, S. Korea
Keywords: Electromagnetic force, non-contacting conveyance, steel strip, position control.
Abstract: Electromagnetic application system to improve the surface quality of steel strip is getting popular because
customers demand better surface quality of steel strip. To realize such a requirement, non-contact
conveyance methods by means of air floater and electromagnetic levitation and propulsion were considered.
However, air floating method is not easy to control of the position of steel strip since the system is highly
nonlinear. And thus, the application of a magnetic levitation and propulsion to steel strip conveyance is
suitable. Sensors measuring positions of steel strip also need to be non-contact in order to maintain non-
contact and simple characteristics of the system. This paper proposes the method of the spatial position
estimation of steel plate without using sensors. This method simplifies non-contact conveyance system and
cuts down expenses of the system. Spatial positions of steel strip can be estimated by currents supplied for
electromagnet to maintain a fixed air gap. Estimated positions are then fed back into the control system to
do position control. Computer simulation and experimental results are provided to verify the suitability of
the proposed system performance and concept.
1 INTRODUCTION
In 1990s, various kinds of research activities were
conducted to convey steel strips by means of non-
contacting methods. One of them was
electromagnetic conveyance technology. At first,
most researchers were focused on reducing vibration
of steel strip. (Liu and Yao, 2002). Later on,
University of Tokyo conducted very promising
research of levitation and propulsion of steel strip
via electromagnetic force. (Hayashiya, and et el,
1999).
Steel making industries produce and treat large
amounts of thin steel strips in cold rolling processes
to obtain high quality steel strips using various ways.
Actually, steel strips are processed at high speed in
continuous cold rolling process lines. Because of
this, vibration and position deviation of steel strip
are the main hazardous problems which cause
surface defects and lower productivity. The non-
contact operation and the quick response mechanism
can be considered to solve the above mentioned
problems. Applications of electromagnetic force can
be one of the useful technical approaches. (Liu and
Yao, 2002).
Electromagnetic application system to improve
the surface quality of steel strip is getting popular
because customers demand better surface quality of
steel strip. To realize such a requirement, non-
contact conveyance methods by means of air floater
and electromagnetic levitation and propulsion were
considered. However, air floating method is not easy
to control of the position of steel strip since the
system is highly nonlinear. And thus, the application
of a magnetic levitation and propulsion to steel strip
conveyance is suitable. Sensors measuring positions
of steel strip also need to be non-contact in order to
maintain non-contact and simple characteristics of
the system. This paper proposes the method of the
spatial position estimation of steel plate without
using sensors. This method simplifies non-contact
conveyance system and cuts down expenses of the
system. Spatial positions of steel strip can be
estimated by currents supplied for electromagnet to
197
Kueon Y., Jin Yoon H. and Su Baek Y. (2008).
POSITION CONTROL METHOD OF A NON-CONTACTING CONVEYANCE SYSTEM FOR STEEL STRIP.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 197-201
DOI: 10.5220/0001489401970201
Copyright
c
 SciTePress

maintain a fixed air gap. Estimated positions are
then fed back into the control system to do position
control. Computer simulation and experimental
results are provided to verify the suitability of the
proposed system performance and concept. (Gerber,
2002)
2 BACKGROUND
Non-contacting conveyance system by means of
electromagnetic force can be seen in Figure 1. The
system should generate normal, thrust, and guidance
forces in order to maintain steel strip under control.
The system is now then designed based on the above
concept.
Steel Plate
Normal Force
Thrust Force
Guidance Force
Iron Core + Coil
U
Figure 1: Non-Contacting System Concept.
Figure 2 shows the schematic diagram of the
non-contact conveyance system.
Ni⋅ shows the
magnetomotive force and
Φ
means magnetic flux.
Reluctance,
ℜ , can be a clearance at the middle of
E-shaped core. Reluctance,
ℜ , can be expressed as
equation (1) in terms of the area, A, at the middle of
E-shaped core. (Roters, 1951).
0
z
A
μ
ℜ=
(1)
where μ
0
c is the permeability in the air which
can be set as
7
410 H/m π
−
×
.
As shown in Figure 1, reluctance on both sides
can be twice as much as the center part of E-shaped
core, since the area on both sides is half of the
middle part. The equivalent reluctance, ℜ
eq
, can be
obtained as shown in equation (2).
1
2
11
22
eq
ℜ=ℜ+ =ℜ
+
ℜℜ
(2)
From equation (2) and Ohm’s law, applied
magnetic field, ℑ, can be expressed by equation (3),
dNiℑ= ⋅ = ⋅
∫
Hl
(3)
10
30
2
2
20 5
Core
Coil
Steel Plate
Levitation
Force, z
Side Sliding
Force, y
Figure 2: Schematic Diagram of the System.
Where N and
i
shows number of turns and applied
current to the coil. Magnetic flux can be computed
by using applied magnetic flux
ℑ
and equivalent
reluctance
eq
ℜ
with Ohm’s law as follows (Trumper,
Weng, Ritter, 1999),
eq eq
N
i
ℑ
Φ= =
ℜ
ℜ
(4)
Hence, flux linkage with
N turns of coils can be
expressed as shown in equation (5).
2
eq
Ni
N
λ =Φ=
ℜ
(5)
Applied current,
i , to the electromagnet can
induce some amount of force to the steel strip. The
induced force to the steel strip can be expressed by
magnetic force, f
e
.
c
e
W
f
z
∂
=
∂
(6)
Where magnetic energy,
c
W , can be obtained as
follows,
0
i
c
Wdt
λ
=
∫
(7)
Equation (7) can be obtained by integrating equation
(5) with respect to time and differentiate partially
with respect to the moving direction. f
e
is induced
force with respect to applied current i and clearance
z.
+
−
NI
ℜ
Φ
2ℜ2
ℜ
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
198

2
2
0
4
e
AN
i
f
z
μ
⎛⎞
=− ⋅
⎜⎟
⎝⎠
(8)
Induced force, f
e
, can be negative when the
electromagnet attracts the thin steel strip. In other
words, attractive force caused by the electromagnet
can be expressed by negative force comparing with
repulsive force (Choi and Baek 2002).
Lim
Steel Plate
Force Sensor
Figure 3: Configuration of the System.
3 SYSTEM DYNAMICS
This paper assumes that the steel strip should keep
constant clearance and perpendicular position during
its movement. The position estimation of the steel
strip cannot be estimated correctly since current
applied to the electromagnet is changed according to
the inclined steel strip. In this paper, two
assumptions were used to derive the equation of
motion between the steel strip and the
electromagnet. They are as follows: one is that the
clearance is always constant, and the other is that the
steel strip is always perpendicular to its moving
direction.
The initial condition of the system is satisfied
when a=0.
A
F
is same as
B
F
and applied current
has also the same amount at the initial condition. If a
is not zero,
A
F
and
B
F
are not the same and
applied current is also not the same, since the
distance between the electromagnet and the center of
gravity of the steel strip is changed and the force
cannot be balanced any more. In other words, the
forces applied to the steel strip from the
electromagnet should be changed to keep the steel
strip perpendicular in accordance with moving
distance. The moving distance or the position of the
steel strip can be estimated by the above mentioned
things. (Nasar and Boldea, 1976).
Figure 4 shows that the steel strip has moved to the
amount of a from the initial position toward x-
direction.
A
F
and
B
F
means the attractive forces to the
points A and B, respectively. In this case, following
two equations can be derived from the force and
moment balance equations.
0;
z A B steel
F
FFF=+=
∑
(9)
0; ( ) ( ) 0
yB A
MFnaFna
=
+− −=
∑
(10)
The above two equations can be expressed in
equation (11), where
s
teel
F is steel strip weight,
s
teel
M
steel strip mass, and g the acceleration of
gravity.
steel steel
FMg
=
× (11)
From equations (9) and (10), the following equation
can be derived with respect to
a ,
B
A
steel
F
F
aq
F
−
=⋅
(12)
The equations about the applied current to each
coil can be derived by using equation (13),
2
2
0
(,)
4
n
n
AN i
F
nAB
z
μ
⎛⎞
==
⎜⎟
⎝⎠
(13)
By substituting equation (13) into equation (12),
the moving position a can be expressed with respect
to the applied current as shown in equation (13),
2
22
0
4
BA
s
teel
AN q
ii
a
F
μ
−
=⋅
(14)
or the following equation can be derived from
equation (8),
22
22
B
A
B
A
ii
aq
ii
−
=⋅
+
(15)
Figure 4: Movement of the Strip.
A
F
Steel
F
a
x
y
z
Initial Postion
q
Postion after moving
B
F
POSITION CONTROL METHOD OF A NON-CONTACTING CONVEYANCE SYSTEM FOR STEEL STRIP
199

4 CONTROL SYSTEM
Levitation force (Normal force) can be described by
y and i
pc
, where y is the air gap between
electromagnetic core and steel strip and i
pc
is DC
offset, respectively. Thrust force can be expressed
by equation (16) and (17), by assuming that the
frequency of power is fixed and AC power alone
takes charge of control. (Fujisaki, 2001).
F
y
= f(y, i
DC
) (16)
F
y
= f(i
AC
) (17)
where, i
AC
is the maximum value of AC current.
Equations of motion can be obtained by the
following:
yKMgFyM
xKFxM
dyy
dxx
&&&
&&&
−−=
−
=
(18)
Where, M is the mass of the strip, F
x
is thrust
force, g is graivity, K
dx
is the friction coefficient in
the x direction, K
dy
is the friction coefficient in the y
direction.
From equations of motion, the following equation
can be obtained.
dBuAxx +
+
=
&
(19)
where,
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
y
x
v
y
v
x
x
,
⎥
⎦
⎤
⎢
⎣
⎡
=
y
x
F
F
u
,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
g
0
0
0
d
,
,
000
1000
000
0010
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
M
K
M
K
dy
dx
A
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
M
M
1
0
00
0
1
00
B
(20)
Control inputs can be derived by the following
equations:
()
xddxxdxdxIxxdxDdxPx
vKaMdtxxKvvKxxKF ++−+−+−=
∫
)()(
(21)
()
yddyydydyIyydyDdyPy
vKaMMgdtyyKvvKyyKF +++−+−+−=
∫
)()(
(22)
where, v
x
and v
y
are velocities in the direction of x
and y, respectively. Feedback gains are as
follows: (Choi and Baek, 2002)
⎥
⎦
⎤
⎢
⎣
⎡
=
000
000
yP
xP
P
K
K
K
,
⎥
⎦
⎤
⎢
⎣
⎡
=
000
000
yI
xI
I
K
K
K
,
and
⎥
⎦
⎤
⎢
⎣
⎡
=
000
000
yD
xD
D
K
K
K
(23)
Now, currents can be applied as follows:
()
02cos +
⋅
⋅
+
=
ftaFFI
xyA
π
(24)
⎟
⎠
⎞
⎜
⎝
⎛
+⋅⋅+=
3
2cos
π
π
ftaFFI
xyB
(25)
⎟
⎠
⎞
⎜
⎝
⎛
+⋅⋅+=
3
2
2cos
π
π
ftaFFI
xyC
(26)
where, a is AC magnitude weighting factor.
The overall control system can be designed as
shown in figure 5.
Figure 5: Control System Diagram.
5 POSITION ESTIMATION OF
STEEL STRIP
The center of gravity of the steel strip is
positioned in the middle of two equal spaced
electromagnets. In this experiment, the steel strip
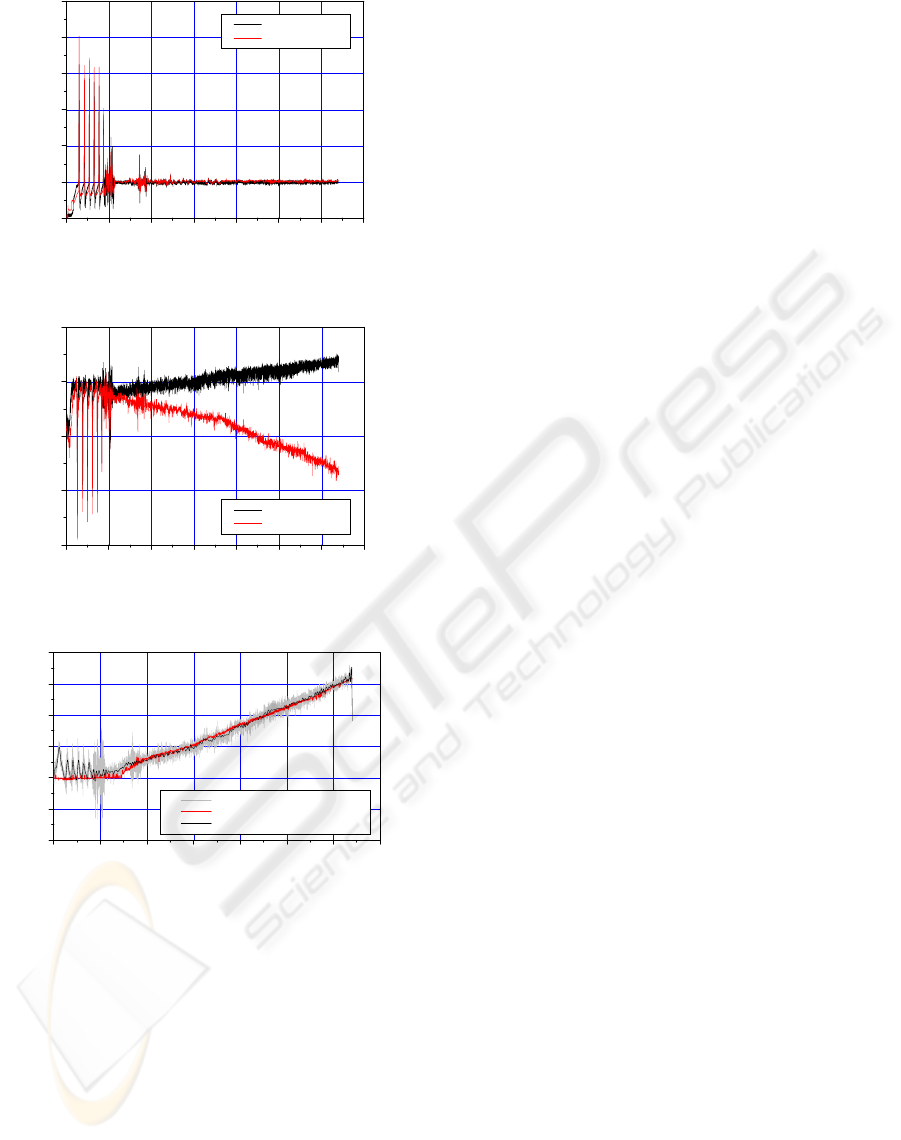
is moving to the x-axis while it is lifted. Figures 6
through 8 show the experimental results. Figure 6
shows that the lifted steel strip can keep the
constant clearance and stable. Figure 7 depicts the
fluctuating current during the steel strip
movements to the x-axis. Figure 8 is the compared
positions of the steel strip as the steel strip moves
to the x-axis. These graphs are the estimated
position, the measured and filtered value by laser
position sensor. (Nakagawa, 2000).
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
200

0 5 10 15 20 25 30 35
0.0
0.2
0.4
0.6
0.8
1.0
1.2
Gap ( mm )
Time ( sec )
Electromagnet A
Electromagnet B
Figure 6: Air gap.
0 5 10 15 20 25 30 35
0.2
0.3
0.4
0.5
0.6
Current ( A )
Time ( sec )
Electromagnet A
Electromagnet B
Figure 7: Current.
0 5 10 15 20 25 30 35
-20
-10
0
10
20
30
40
Diplacement ( mm )
Time ( sec )
Proposed method
LDS
Proposed method with filter
Figure 8: Position of a Moving Steel Strip.
6 RESULTS
A non-contact conveyance of the steel strip by
electromagnets has been proposed to show that the
applied current can be changed in accordance with
the movement of the levitated steel strip.
The position estimation method of the steel strip by
the applied current has also been proposed and
tested in the constructed non-contact steel strip
conveyance system. The estimated position of the
steel strip has been compared the measured one by a
laser position sensor. The estimated position of the
steel strip shows satisfactory results comparing with
the measured one. Non-contact sensors are very
expensive and some of them make system
complicated. To eliminate sensors, this paper
proposes the method of the spatial position
estimation of steel strip without sensors. This
method simplifies non-contact conveyance system
and cuts down expenses. The spatial position of steel
strip with currents supplied for electromagnet was
estimated and used to maintain a fixed air gap. And
the theoretical analysis was verified by experiments
and shows good control performance.
REFERENCES
H. Hayashiya, N. Araki, J. E. Paddison, H. Ohsaki, and E.
Masada, 1996, IEEE Trans. Magn., Vol. 32, pp.5052-
5054.
Herbert C. Roters, 1951, Electromagnetic Devices, John
wiley & sons.
Cheng-Tseng Liu and Sung-Yi Yao, 2002, IEEE
Transactions on Magnetics, Vol. 38, No. 5.
Howard L. Gerber, 2002, IEEE 2002.
Keisuke Fujisaki, 2001, IEEE Transactions on Industry
Applications, Vol. 37, No. 4.
Keisuke Fujisaki, 2002, IEEE 2002.
Siegfried Latzel, 20000, IEEE 2000.
Cheng-Tsung Liu and Sung-Yi Yao., 2002.
Electromagnetic Field and Force Analyses of a Non-
contacting Conveyance System for Steel Mill
Application, IEEE Transactions on Magnetics, VOL.,
38, NO. 5.
Keisuke Fujisaki., 2000. Application of Electromagnetic
Force to Run Out Table., IEEE.
K. Fujisake, T. Ueyama, and K. Wajima, 1996.
Electromagnets Applied to Thin Steel Plate, IEEE
Transaction on Magnetics, Vol. Mag-32.
Shinya Hasegawa, Takayuki Obata, Yasuo Oshinoya, and
Kazuhisa Ishibashi, 2002, “Study on Noncontact
Support and Transportaion of a Rectangular Thin Steel
Plate, Proc. Schl. Eng. Tokai Univ., Ser. E, 27, pp. 1 – 12.
Toshiko Nakagawa, Mikio Hama, and Tadashi Furukawa,
2000, IEEE Trans. on Magnetics, Vol. 36, No. 5, pp.
3686 – 3689.
David L. Trumper, Ming-chih Weng, and Robert J. Ritter,
1999, Proceedings of the IEEE International
Conference on Control Applications, pp. 551 – 557.
Herbert C. Roters, 1941, Electromagnetic Devices, John
Wiley & Sons, Inc., .
S. A. Nasar and I. Boldea, 1976, Linear Motion Electric
Machines, John Wiley & Sons.
Jung Soo Choi and Yoon Su Baek, 2002, KSME
International Journal, Vol. 16, No. 12, pp. 1643 – 1651,
2002.
POSITION CONTROL METHOD OF A NON-CONTACTING CONVEYANCE SYSTEM FOR STEEL STRIP
201