REDUCED ORDER H
∞
SYNTHESIS USING A PARTICLE
SWARM OPTIMIZATION METHOD
Guillaume Sandou, Gilles Duc and Patrick Boucher
Supelec Automatic Control Department, 3 rue Joliot Curie, 91192 Gif-sur-Yvette, France
Keywords: Particle swarm optimization, Reduced-order H
∞
synthesis, metaheuristics.
Abstract: H
∞
controller synthesis is a well known design method for which efficient dedicated methods have been
developed. However, such methods compute a full order controller which has often to be reduced to be
implemented. Indeed, the reduced order H
∞
synthesis is a non convex optimization problem due to rank
constraints. In this paper, a particle swarm optimization method is used to solve such a problem. Numerical
results show that the computed controller has a lower H
∞
norm than the controller computed from a classical
Hankel reduction of the full order H
∞
controller.
1 INTRODUCTION
H
∞
synthesis is an efficient tool, which aims to
compute controllers in a closed loop framework,
achieving high and various performances. Two
principal solution methods have been developed for
this purpose, based on Linear Matrix Inequalities
(Gahinet and Apkarian, 1994), or on Riccatti
equation solutions (Glover and Doyle, 1988). The
main drawback of such approaches is the controller
order: H
∞
synthesis provides a controller whose
order is the same as the synthesis model. A classical
way to get low order controllers is to reduce the full
controller, for example with a Hankel decomposition
method. However, this approach may lead to a high
H
∞
norm of the closed loop system and a high
sensitivity to high frequency noises. To avoid high
order controllers, the H
∞
optimization problem can
be solved, adding some order constraints. However,
this kind of constraints is expressed with rank
constraints and the reduced-order synthesis problem
appears to be a non convex optimization problem,
and classical algorithms may fail in the solution.
In this paper, a new approach is proposed, using
Particle Swarm Optimization (PSO). With such a
method, the optimality of the computed solution can
never be guaranteed, but the structure of costs and
constraints is not an essential point. The
mathematical descriptions of the full and reduced
order H
∞
synthesis are called up in section 2. PSO is
presented in section 3. The proposed algorithm is
used for the multivariable control of a pendulum in
the cart. Results are given in section 4. Finally
conclusions are drawn in section 5.
2 REDUCED-ORDER H
∞
SYNTHESIS
2.1 Full-Order H
∞
Synthesis
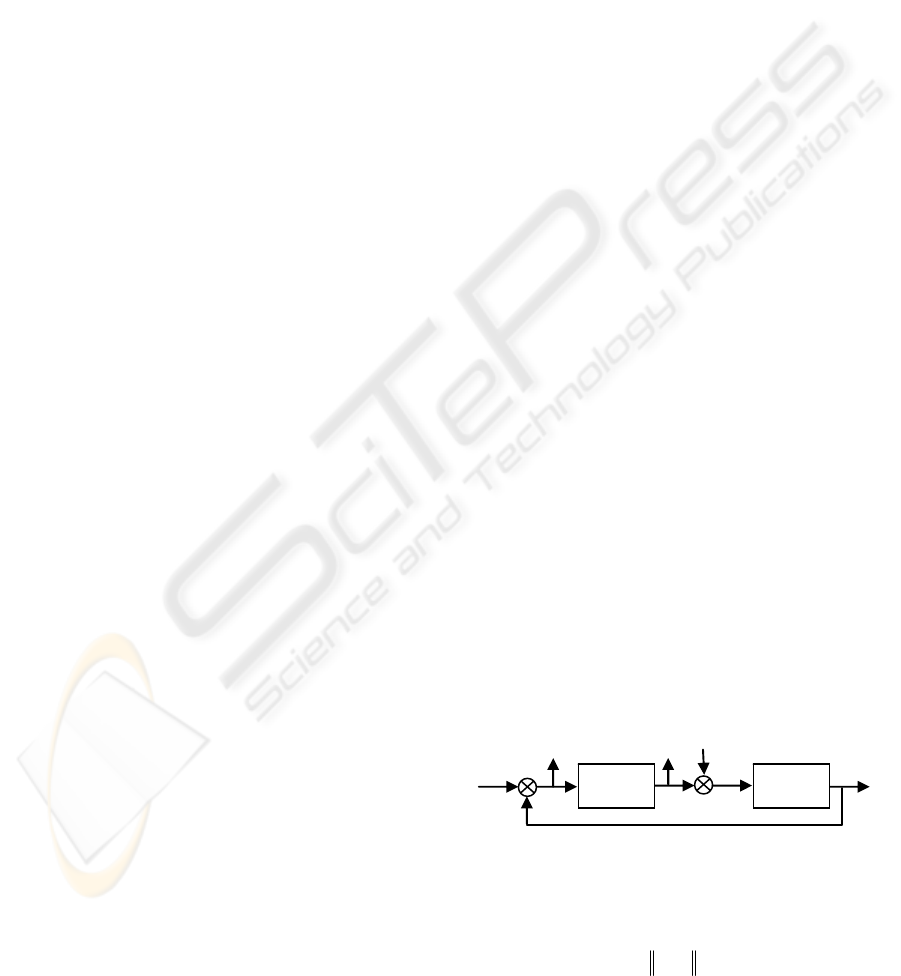
Consider the closed loop of figure 1, with
s
the
Laplace variable. The transfer matrix is:
1
)()(()(with
)(
)(
)(
)(
)(
)(
)(
−
+=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
sKsGIsS
sd
sr
sT
sd
sr
KSGKS
SGS
su
s
ε
(1)
)(sG
)(sK
+
+ +
-
r
ε u
d
v
y
Figure 1: Classical closed loop system.
The H
∞
synthesis problem is defined as follows.
Find a stabilizing controller
)(sK such that:
∞
= )(min
)(
sT
sK
γ
(2)
302
Sandou G., Duc G. and Boucher P. (2008).
REDUCED ORDER H∞ SYNTHESIS USING A PARTICLE SWARM OPTIMIZATION METHOD.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 302-305
DOI: 10.5220/0001489703020305
Copyright
c
SciTePress
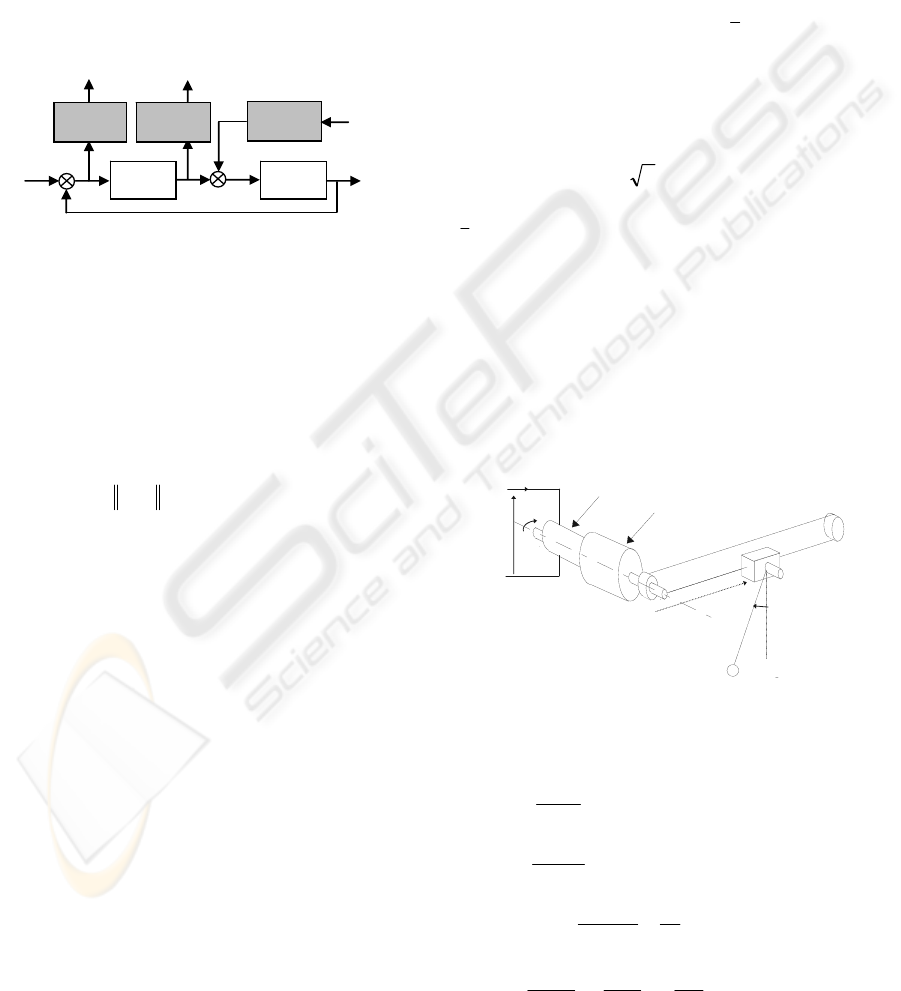
It can be reformulated into a convex problem and
solved with Riccati equations or LMI formulations.
This solution is called “full order” synthesis, as the
solution of problem (2) is a controller
)( sK
whose
order is equal to the order of
)(sG . Some design
filters are added to the synthesis model to tune the
performances (figure 2). The new system is:
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
)(
)(
)(
)(
322
311
2
1
sd
sr
KSGWWKSW
SGWWSW
se
se
(3)
)(sG
)(sK
+
+ +
-
r
ε
u
d
v
y
)(
1
sW
)(
2
sW
)(
3
sW
1
e
2
e
3
e
Figure 2: Synthesis model.
Finally, solving the H
∞
problem for this system
induces frequency dependent constraints for each
transfer of matrix (1).
2.2 Reduced-Order H
∞
Synthesis
The reduced-order H
∞
problem refers to the solution
of the following optimization problem:
r
sK
nsKsTγ =∂°=
∞
)(.s.t)(min
)(
(4)
where
K∂° denotes the order of )(sK , and
r
n is
strictly less than the order of the synthesis model. It
can be reformulated into LMI equations by adding
rank constraints on matrices, loosing the property of
convexity (El Ghaoui et al., 1997).
3 PSO ALGORITHM
PSO was introduced by Russel and Eberhart
(Eberhart and Kennedy, 1995). P particles are
moving in the search space.
k
p
x
(
k
p
v
) is the position
(velocity) of particle p at iteration k,
k
p
b is the best
position found by particle p until iteration k,
},,2,1{)( PxV
k
p
K⊂ is the set of “friend particles”
of particle p at iteration k,
k
p
g best position found by
the friend particles of particle p until iteration k, and
⊗
element wise multiplication of vectors. The
particles move in the search space according to the
following transition rule:
11
2
1
1
)(
)(.
++
+
+=
−⊗+
−⊗+=
k
p
k
p
k
p
k
p
k
p
k
p
k
p
k
p
k
p
vxx
xgc
xbcvwv
(5)
In this equation,
w
is the inertia factor and
21
, cc are
random vectors in the range
],0[ c
. The choice of
parameters is very important to ensure the satisfying
convergence of the algorithm, see (Eberhart and Shi,
2000). However, it is not in the scope of this study to
look for fine strategies of tuning. Thus, standard
values, given in (Kennedy and Clerc, 2006) will be
used
P
: nP += 10 (
n
is the number of
optimization variables),
))2ln(2/(1=w ,
)2ln(5,0 +=c , 3))(dim( ≤
k
p
xV .
4 NUMERICAL RESULTS
4.1 Case Study
The proposed method has been tested for a
pendulum in the cart (figure 3).
Moteur
Réducteur
Génératrice
tachymétrique
Potentiomètre
Potentiomètre
Charge
Chariot
u
i
ϕ
x
c
ω
Motor
Reduction
Cart
Pendulum
Figure 3: Pendulum in the cart.
The system can be modelled by:
)()()(
)(
tutωKtiR
td
tid
L
e
=++
)()()(
)(
tiKtdtωf
td
tωd
J
e
=++
)(
)(
tω
N
r
td
txd
c
=
0)(sin)(cos
2
2
2
2
=+++ φg
td
φd
α
td
φd
l
td
xd
φ
c
(6)
REDUCED ORDER H8 SYNTHESIS USING A PARTICLE SWARM OPTIMIZATION METHOD
303
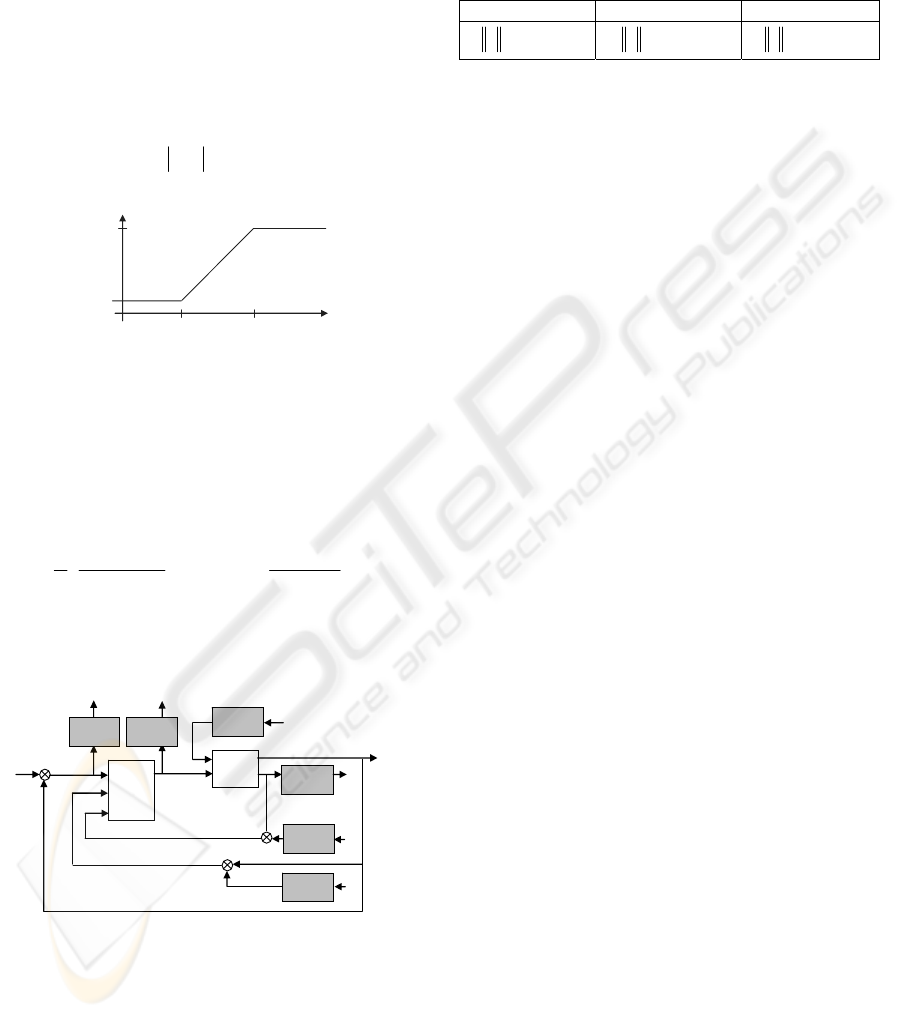
Variables are
i and u (current and input voltage of
the motor), ω (rotation speed),
c
x (position of the
cart),
φ (angle of the pendulum), d (disturbance
moment). Constants are
JRL ,, (motor inductor,
resistance, inertia),
e
K (electromagnetic constant),
f (friction coefficient),
r
(pulley radius), N (gear
reduction),
l (pendulum length), α (pendulum
friction coefficient) and
g
(weight acceleration).
Specifications are: tracking of the reference of figure
4, no steady state error, time response
≤
6s, rejection
of disturbance
d and
rad05.0)( ≤tφ
;
time
Position reference
0,4 m
0
0
4s
Figure 4: Position reference.
4.2 Three Outputs H
∞
Synthesis
To show the versatility of the method, a three
measurement controller is designed (synthesis model
of figure 5). The filters are defined as:
0009.0
7.1
2
1
1
+
+
⋅=
s
s
W
,
2000
2
100
2
+
+
⋅=
s
s
W
01.0
3
=W , 2
4
=W , 1
5
=W , 1.0
6
=W
(8)
)(sG
)(sK
+
-
r
ε
u
d
φ
)(
1
sW
)(
2
sW
)(
3
sW
1
e
2
e
3
e
c
x
)(
4
sW
4
e
)(
5
sW
5
e
)(
6
sW
6
e
-
-
+
+
Figure 5: Synthesis model for the “3 output” case.
The solution of the full order synthesis leads to a H
∞
norm
06.1=γ . The full-order controller is of order
6. The Hankel reduction leads to a very large H
∞
norm
7.56=γ for the order 2 controller. A
controller is computed by the PSO algorithm, with
the filters of the full order synthesis. Results are
given in table 1 for 100 tests. Computation times are
30s (Pentium IV, 2GHz; Matlab 6.5).
Table 1: Optimisation results for the three output case.
Worst Best Mean
53.4=
∞
60.2=
∞
50.3=
∞
Figure 6 gives the Bode diagram of the transfers of
matrix (1) (full order, Hankel reduction controller,
and PSO). Figure 7 represents the corresponding
time responses. As can be seen, results of the Hankel
reduction controller are quite similar as for the full
order controller, except at high frequencies. Figure 8
and 9 give the same results obtained with the mean
controller of the PSO method. Note first that the
response of
)(tφ is quite similar as the previous
ones and remains therefore satisfying. A slight
overshoot is observed on the reference tracking.
However, consider figure 10, where a
measurement noise
m
d has been added on the cart
position. The control input u is represented both for
Hankel reduction and PSO controllers. As can be
seen from figure 6, Hankel reduction leads to a
modification of the closed loop transfers for high
frequencies. As a result, high gains for high
frequencies lead to an amplification of measurement
noises and thus to chattering control inputs. On the
contrary, the reduced order synthesis leads to closed
loop systems with smaller H
∞
norm. The system is
more robust against measurement disturbances.
5 CONCLUSIONS
In this paper, a metaheuristic method based on
Particle Swarm Optimization has been presented.
PSO is a stochastic optimization method which does
not require any particular structure for costs and
constraints. As a result, the method can be used to
optimize many kinds of criterions and solve non
convex, non linear or non analytic problems. In this
paper, the method is used to solve a well known
problem of modern Automatic Control, namely the
reduced order H
∞
synthesis. The problem is known
to be a non convex problem, for which the
traditional approach is an a posteriori reduction of
the full order synthesis. Results, computed for a
pendulum in the cart have shown the viability of the
approach. Computed controllers lead to a slight
decrease of nominal performances but to a more
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
304
robust controller with an important decrease of the
closed loop H
∞
norm.
10
-5
10
0
10
5
10
-4
10
-2
10
0
10
2
vr --> eps and gamma/W1
10
-5
10
0
10
5
10
-5
10
0
10
5
vr --> u and gamma/W2
10
-5
10
0
10
5
10
-5
10
0
10
5
d -- > eps and gamma/W 1/ W3
10
-5
10
0
10
5
10
-10
10
-5
10
0
10
5
d --> u and gamma/W 1/W2
Full order
bound
Hankel reduc tion
Figure 6: Bode transfer of full order and Hankel reduction.
0 5 10 15 20 25
-0.4
-0.2
0
0.2
0.4
Cart Position
Refer enc e
Full order
Hankel reduc tion
0 5 10 15 20 25
-0.04
-0.02
0
0.02
0.04
Pendulum angle
Figure 7: Time response - full order and Hankel reduction.
10
-5
10
0
10
5
10
-5
10
0
10
5
vr --> eps
10
-5
10
0
10
5
10
-5
10
0
vr --> u
10
-5
10
0
10
5
10
-5
10
0
10
5
d --> eps
10
-5
10
0
10
5
10
-10
10
-5
10
0
10
5
d --> u
Figure 8: Bode transfer for PSO controller.
0 5 10 15 20 25
-0.4
-0.2
0
0.2
0.4
Cart Position
Referenc e
PSO reduction
0 5 10 15 20 25
-0.04
-0.02
0
0.02
0.04
Pendulum angle
Figure 9: Time response for PSO controller.
0 5 10 15 20 25
-4
-2
0
2
4
u for Hankel reduction controller
0 5 10 15 20 25
-4
-2
0
2
4
u for PSO controller
Figure 10: Control input for Hankel reduction and PSO
controllers.
REFERENCES
Eberhart, R. C, Kennedy, J., 1995. A new optimizer using
particle swarm theory. In: Proceedings of the Sixth
International Symposium on Micromachine and
Human Science, Nagoya, Japan. pp. 39-43.
Eberhart, R. C., Shi, Y., 2000. Comparing inertia weigthts
and constriction factors in particle swarm
optimization. Proceedings of the IEEE Congress on
Evolutionary Computation (CEC 2000), San Diego,
CA, USA, p 84-88.
El Ghaoui, L., Oustry, F., AitRami, M., 1997. A cone
complementary linearization algorithm for static
output feedback and related problems. In: IEEE
Transactions on Automatic Control, Vol. 42(8), pp.
1171-1176.
Gahinet, P., Apkarian P., 1994. A linear matrix inequality
approach to H
∞
control. In International Journal of
Robust and Nonlinear Control, Vol. 4, pp. 421-448.
Glover, K., Doyle, J.C., 1988. State-state formulae for all
stabilizing controllers that satisfy an H
∞
-norm bound
and relations to risk sensitivity. In Systems and
Control Letters, Vol.11, pp. 167-172.
Kennedy, J. and M. Clerc, 2006. Standard PSO.
http://www.particleswarm.info/Standard_PSO_2006.c
REDUCED ORDER H8 SYNTHESIS USING A PARTICLE SWARM OPTIMIZATION METHOD
305
