DETECTION AND CONTROL OF NON-LINEAR BEHAVIOR BY
SLIDING MODES CONTROL IN A 3 D.O.F. ROBOT
Claudio Urrea and Marcela Jamett
Departamento de Ingeniería Eléctrica, Universidad de Santiago de Chile (USACH)
Av. Ecuador 3519, Santiago, Chile
Keywords: Planar Robot Model, Chaotic behaviour, Sliding Modes.
Abstract: Results from simulations of a Planar Robot Model, when it is placed in the same plane of the action of the
gravity force are reviewed in this paper. The model includes several parameters usually discarded in current
models, such as Driving, and Non-linear Friction, for an industrial-type robotic manipulator and its
actuators. When we develop more exact representations of the dynamics of a manipulator and their
actuators, chaotic behavior is detected for certain parameter values of the robotic manipulator. This chaotic
behavior – without external inputs – was exactly controlled by Sliding Modes.
1 INTRODUCTION
A variable structure system (VSS) is a system whose
structure is intentionally changed to achieve the
desired performance. This intentional structural
change is typically accomplished through
discontinuous control action in accordance with a
presigned algorithm and switching hyperplanes
(Zohdy, M., Fadali, M.S. and Liu, J., 1992).
For nonlinear dynamical systems with
uncertainties and disturbance, the sliding modes
control (SMC) is a method which has some
advantages. The SMC was proposed and elaborated
initially in the fifties in the former Soviet Union
(Park, D. and Choi, S., 1999). This control method,
which can be obtained by an appropriate
discontinuous law, is the principal operation mode in
the variable structure control system (VSCS). This
method is known for its robustness to disturbance
and parameters variations (Bartoszewicz, A., 1995).
The sliding mode controllers have excellent
characteristic in the sliding movement of the state on
the sliding surface. During this sliding movement,
the system has invariants properties, producing a
robust movement regarding the unknown parameters
of the system and the external interferences. The
design of the VSS based sliding mode controllers
can be broken down into two major phases: the first
one is the determination of a stable manifold, called
the sliding surface, and the second phase is to design
a switching control law according to the sliding
surface to satisfy the attraction manifold. When the
sliding mode occurs, the system state will remain on
it forever and the system behaves as an equivalent
system with desired dynamics which is governed by
the sliding surface equation; at the same time the
system has good characteristics such as fast
response, good robustness and disturbance rejection,
etc. (Xu, J., Lee, T.H., Wang, M. and Yu, X., 1996).
Efficient control of industrial robots is an
important issue to success of industrial automation
in these years (Lu, X. and Spurgeon, S., 1999).
Along with the development of robot manipulator
control theory and its applications, there has been
increasing demand for more efficient control
schemes to achieve satisfactory results (Chen, C. and
Xu, R., 1999).
The paper is organized as follows: in section 2, a
friction model is given. In section 3, manipulator
dynamic equations are presented. In section 4, the
state-space model for a 3 link planar robot and its
actuators, is developed. In section 5, the robot
controller is developed. Section 6 presents some
simulation results. Finally, in section 7, the
conclusions are discussed.
2 FRICTION MODEL
Models representing friction effects have been
widely studied in concerned literature (Canudas, C.,
Aström, K. and Braun, K., 1987), (Kircanski, N. and
71
Urrea C. and Jamett M. (2008).
DETECTION AND CONTROL OF NON-LINEAR BEHAVIOR BY SLIDING MODES CONTROL IN A 3 D.O.F. ROBOT.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 71-76
DOI: 10.5220/0001490100710076
Copyright
c
 SciTePress

Goldenberg, A., 1997), (Urrea, C., 1999). In this
paper, we use a model that includes both effects,
whose friction curve is discontinuous and non-
symmetrical.
θ)()
)θ(
()θ(
210
θ
0
2




⋅
α
+⋅⋅
α
+
α
= sgn
v
F
e
(1)
where:
)θ(

F : is the friction torque [N · m]; θ

:
angular velocity [rad
/ s]; α
0
+ α
1
: static friction [N ·
m]; v
0
: Stribeck velocity [rad / s]; α
2
: viscous friction
[N
· m · s / rad].
3 MANIPULATOR DYNAMIC
EQUATIONS
The dynamic equation of a robotic manipulator in
the joint space can be written as follows (Leahy, M.,
Valavanis, K. and Saridis, G., 1989); (
Mahla, I.,
Urrea, C., 1999):
τBD =+⋅ )θ,θ(θ)θ(

(2)
where:
)θ()θ(θ)θ,θ()θ,θ( GFCB ++⋅=

(3)
in which
θ : joint angle vector,
n
R∈θ
; )θ(D :
inertial matrix,
nxn
RD ∈θ)(
;
)θ,(θ

C
: Coriolis and
centrifugal torque matrix,
nxn
RC ∈)θ,θ(

; )θ(G :
gravity torque vector,
n
RG ∈θ)( ;
τ
: joint torque
vector,
n
R∈
τ
; n : degrees of freedom.
4 STATE-SPACE MODELS
4.1 Manipulator
If in an industrial-type robotic manipulator, the
following state variables are chosen:
x
1
= θ
1
; x
2
=
θ

1
; x
3
= θ
2
;
x
4
=
θ

2
; x
5
=θ
3
; x
6
=
θ

3
(4)
then:
x

2
=
θ

1
; x

4
=
θ

2
, ; x

6
=
θ

3
(5)
If some of the elements in the inertial matrix
D(θ(t)) are defined as constants, there it is obtained:
k
1
= m
1
· l
c1
+ (m
2
+ m
3
) · l
1
(6)
k
2
= m
2
· l
c2
+ m
3
· l
2
(7)
k
3
= m
3
· l
3
(8)
where
m
1
: mass of the first link [kg]; m
2
: mass of
the second link [kg]; m
3
: mass of the third link [kg];
l
1
: length of the first link [m]; l
2
: length of the
second link [m];
l
3
: length of the third link [m]; l
c1
:
distance between the gravity centre of the first link
and its driving axis [m];
l
c2
: distance between the
gravity centre of the second link and its driving axis
[m]. Replacing eq. 1 and eqs. 4 to 8 into eqs. 2 and 3
(n = 3), we have:
τ
L1
*
=
(
I
1
+ I
2
+ I
3
+ m
1
· l
c1
2
+ m
2
· (l
1
2
+
l
c2
2
) + m
3
· (l
1
2
+ l
2
2
+ l
c3
2
) + 2 · k
2
·
l
1
· cos x
3
+ 2 · k
3
· ( l
1
· cos ( x
3
+ x
5
)
+ l
2
· cos ( x
5
))) ·
x

2
/ N
1
+ ( I
2
+ I
3
+
m
2
· l
c2
2
+ m
3
· ( l
2
2
+ l
c3
2
) + k
2
· l
1
·
cos ( x
3
) + k
3
· ( l
1
· cos ( x
3
+ x
5
) + 2 ·
l
2
· cos ( x
5
))) ·
x

4
/ N
1
+ ( I
3
+ m
3
· l
c3
2
+ k
3
· (l
1
· cos ( x
3
+ x
5
) + l
2
· cos ( x
5
)))
·x

6
/ N
1
+ ( k
2
· ( - l
1
· sin ( x
3
) · ( 2 · x
2
·
x
4
+ x
4
2
)) + k
3
· ( - l
1
· sin ( x
3
+ x
5
) ·
( 2 · x
2
· ( x
4
+ x
6
) + ( x
4
+ x
6
)
2
) - l
1
·
sin ( x
5
) · ( 2 · ( x
2
+ x
4
) · x
6
+ x
6
2
))) / N
1
+ g ·( k
1
· cos ( x
1
) + k
2
· cos ( x
1
+ x
3
) +
k
3
· cos ( x
1
+ x
3
+ x
5
)) / N
1
+ F
1
( x
2
) /
N
1
(9)
τ
L2
*
=
(
I
2
+ I
3
+ m
2
· l
c2
2
+ m
3
· ( l
2
2
+ l
c3
2
) +
k
2
·( l
1
· cos ( x
3
) + k
3
· ( l
1
· cos ( x
3
+
x
5
) + 2 · l
2
·cos (x
5
))) ·
x

2
/ N
2
+ ( I
2
+
I
3
+ m
2
· l
c2
2
+ m
3
· (l
2
2
+ l
c3
2
) + k
3
· 2 ·
l
2
· cos ( x
5
)) ·x

4
/ N
2
+ ( I
3
+ m
3
· l
c3
2
+ k
3
· l
2
· cos ( x
5
)) ·
x

6
/ N
2
+ ( k
2
· ( l
1
·
sin ( x
3
+ x
5
) · x
2
2
) + k
3
· ( l
1
· sin ( x
3
+
x
5
) · x
2
2
- l
2
· sin ( x
6
) · ( 2 · ( x
2
+ x
4
) ·
x
6
+ x
6
2
))) / N
2
+ g · ( k
2
· cos ( x
1
+ x
3
)
+
k
3
· cos ( x
1
+ x
3
+ x
5
)) / N
2
+ F
2
( x
4
)
/ N
2
(10)
τ
L3
*
=
(
I
3
+ m
3
· l
c3
2
+ k
3
· (l
1
· cos ( x
3
+ x
5
)
+ l
2
·cos ( x
5
))) ·x

2
/ N
3
+ ( I
3
+ m
3
·
l
c3
2
+ k
3
· l
2
·cos ( x
5
)) ·
x

4
/ N
3
+ ( I
3
+ k
3
2
) · x

6
/ N
3
+ k
3
· ( l
1
· sin ( x
3
+ x
5
)
· x
2
2
+ l
2
· sin ( x
5
) · ( x
2
+ x
4
)
2
) / N
3
+ g
· k
3
· cos ( x
1
+ x
3
+ x
5
) / N
3
+ F
3
( x
6
) /
N
3
(11)
where τ
L1
*
: torque applied in the first link, referred
to the first motor axis [N
· m]; τ
L2
*
: torque applied in
the second link, referred to the second motor axis [N
· m]; τ
L3
*
: torque applied in the third link, referred to
the third motor axis [N
· m]; N
1
: reduction factor of
the first gear train;
N
2
: reduction factor of the
second gear train; N
3
: reduction factor of the third
gear train; I
1
: moment of inertia of the first link [Kg ·
m]; I
2
: moment of inertia of the second link [Kg · m];
I
3
: moment of inertia of the third link [Kg · m]; F
1
: is
the friction torque in the first link axis, [N
· m]; F
2
: is
the friction torque in the second link axis, [N
· m];
F
3
: is the friction torque in the third link axis, [N ·
m]; g : is the gravity force [N · m].
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
72

Defining the following functions:
f
1
*
= ( I
1
+ I
2
+ I
3
+ m
1
· l
c1
2
+ m
2
· (l
1
2
+
l
2
2
) + m
3
· (l
1
2
+ l
2
2
+ l
c3
2
) + 2 · k
2
· l
1
· cos
x
3
+ 2 · k
3
· ( l
1
· cos ( x
3
+ x
5
) + l
2
·
cos ( x
5
))) / N
1
(12)
f
2
*
= ( I
2
+ I
3
+ m
2
· l
c2
2
+ m
3
· ( l
2
2
+ l
c3
2
) +
k
2
· l
1
· cos ( x
3
) + k
3
· ( l
1
· cos( x
3
+ x
5
)
+ 2 · l
2
· cos ( x
5
))) / N
1
(13)
f
3
*
= ( I
3
+ m
3
· l
c3
2
+ k
3
· (l
1
· cos ( x
3
+ x
5
)
+ l
2
· cos ( x
5
))) / N
1
(14)
f
4
*
= ( k
2
· ( l
1
· sin ( x
3
) · ( 2 · x
2
· x
4
+ x
4
2
)) + k
3
· ( l
1
· sin ( x
3
+ x
5
) · ( 2 · x
2
· ( x
4
+ x
6
) +
( x
4
+ x
6
)
2
) + l
1
· sin ( x
5
) · ( 2 · ( x
2
+ x
4
) ·
x
6
+ x
6
2
))) /N
1
- g · ( k
1
· cos ( x
1
) + k
2
· cos
( x
1
+ x
3
) + k
3
· cos ( x
1
+ x
3
+ x
5
)) / N
1
-
F
1
( x
2
) / N
1
(15)
f
5
*
= ( I
2
+ I
3
+ m
2
· l
c2
2
+ m
3
· ( l
2
2
+ l
c3
2
) +
k
2
· ( l
1
· cos ( x
3
) + k
3
· ( l
1
· cos( x
3
+
x
5
) + 2 · l
2
· cos ( x
5
))) / N
2
(16)
f
6
*
= ( I
2
+ I
3
+ m
2
· l
c2
2
+ m
3
· (l
2
2
+ l
c3
2
) +
k
3
· 2 · l
2
· cos ( x
5
)) / N
2
(17)
f
7
*
= ( I
3
+ m
3
· l
c3
2
+ k
3
· l
2
· cos (x
5
)) / N
2
(18)
f
8
*
= - ( k
2
· ( l
1
· sin ( x
3
+ x
5
) · x
2
2
) + k
3
· ( l
1
·
sin ( x
3
+ x
5
) · x
2
2
) - l
2
· sin ( x
6
) · ( 2 ·
( x
2
+ x
4
) · x
6
+ x
6
2
))) / N
2
- g · ( k
2
· cos
( x
1
+ x
3
) + k
3
· cos ( x
1
+ x
3
+ x
5
) / N
2
- F
2
( x
4
) / N
2
(19)
f
9
*
= ( I
3
+ m
3
· l
c3
2
+ k
3
· (l
1
· cos ( x
3
+ x
5
)
+ l
2
· cos ( x
5
))) / N
3
(20)
f
10
*
= ( I
3
+ m
3
· l
c3
2
+ k
3
· l
2
· cos ( x
5
)) / N
3
(21)
f
11
*
= ( I
3
+ k
3
2
) / N
3
(22)
f
12
*
=
then:
- k
3
· ( l
1
· sin ( x
3
+ x
5
) · x
2
2
+ l
2
· sin
( x
5
) · ( x
2
+ x
4
)
2
) / N
3
- g · k
3
· cos ( x
1
+
x
3
+ x
5
) / N
3
- F
3
( x
6
) / N
3
(23)
τ
L1
*
+ f
4
*
=
f
1
*
· x

2
+ f
2
*
· x

4
+ f
3
*
· x

6
(24)
τ
L2
*
+ f
8
*
=
f
5
*
·x

2
+ f
6
*
·x

4
+ f
7
*
·x

6
(25)
τ
L3
*
+ f
12
*
= f
9
*
· x

2
+ f
10
*
· x

4
+ f
11
*
· x

6
(26)
Defining:
f
13
*
= 1/[ f
3
*
· f
5
*
· f
10
*
- f
3
*
· f
9
*
· f
6
*
- f
2
*
· f
5
*
· f
11
*
- f
2
*
· f
9
*
· f
7
*
· f
6
*
· f
11
*
-
f
1
*
· f
10
*
· f
7
*
]
(27)
f
14
*
= f
13
*
· [ f
6
*
· f
11
*
- f
10
*
· f
7
*
] (28)
f
15
*
= f
13
*
· [ f
9
*
· f
7
*
- f
5
*
· f
11
*
] (29)
f
16
*
= f
13
*
· [ f
5
*
· f
10
*
- f
9
*
· f
6
*
] (30)
f
17
*
= f
13
*
· [ f
3
*
· f
10
*
- f
2
*
· f
11
*
] (31)
f
18
*
= f
13
*
· [ f
1
*
· f
11
*
- f
3
*
· f
9
*
] (32)
f
19
*
= f
13
*
· [ f
2
*
· f
9
*
- f
1
*
· f
10
*
] (33)
f
20
*
= f
13
*
· [ f
2
*
· f
7
*
- f
3
*
· f
6
*
] (34)
f
21
*
= f
13
*
· [ f
3
*
· f
5
*
- f
1
*
· f
7
*
] (35)
f
22
*
= f
13
*
· [ f
1
*
· f
6
*
- f
2
*
· f
5
*
] (36)
Redefining functions,
f
23
*
= f
14
*
· f
4
*
(37)
f
24
*
= f
15
*
· f
8
*
(38)
f
25
*
= f
16
*
· f
12
*
(39)
f
26
*
= f
17
*
· f
4
*
(40)
f
27
*
= f
18
*
· f
8
*
(41)
f
28
*
= f
19
*
· f
12
*
(42)
f
29
*
= f
20
*
· f
4
*
(43)
f
30
*
= f
21
*
· f
8
*
(44)
f
31
*
= f
22
*
· f
12
*
(45)
The state equation model for the three-link
planar RRR arm can be written as:
x

1
=
x
2
(46)
x

2
=
f
14
*
· τ
L1
*
+ f
23
*
+ f
15
*
· τ
L2
*
+ f
24
*
+ f
16
*
· τ
L3
*
+ f
25
*
(47)
x

3
=
x
4
(48)
x

4
=
f
17
*
· τ
L1
*
+ f
26
*
+ f
18
*
· τ
L2
*
+ f
27
*
+ f
19
*
· τ
L3
*
+ f
28
*
(49)
x

5
=
x
6
(50)
x

6
=
f
20
*
· τ
L1
*
+ f
29
*
+ f
21
*
· τ
L2
*
+ f
30
*
+ f
22
*
· τ
L3
*
+ f
31
*
(51)
4.2 Actuators
By employing state equations models for three DC
motors, and from (Craig, J., 1996), we have
equations (52) to (54):
x

7
=
[
k
a1
· v
a1
(t)
−
r
a1
· x
7
−
k
a1
· k
b1
· x
2
·
N
1
] / L
a1
(52)
x

8
=
[
k
a2
· v
a2
(t)
−
r
a2
· x
8
−
k
a2
· k
b2
· x
4
·
N
2
] / L
a2
(53)
x

9
=
[
k
a3
· v
a3
(t)
−
r
a3
· x
9
−
k
a3
· k
b3
· x
6
·
N
3
] / L
a3
(54)
where
k
aj
: proportional j-motor-torque constant
[N
· m / A]; v
aj
: armature voltage [V]; r
aj
: j-motor
armature resistance [Ω];
x
j+6
= τ
j
: torque generated
by the
j-motor axis [N · m]; k
bj
: j-motor
proportionality constant [V
· rad / s]; L
aj
: j-motor
armature inductance [H];
with j = 1, 2, 3.
DETECTION AND CONTROL OF NON-LINEAR BEHAVIOR BY SLIDING MODES CONTROL IN A 3 D.O.F.
ROBOT
73

4.3 State Equations Model
The torque generated in the j-motor axis is equal to
the sum of the
j-motor and its load, i.e.:
)θ()(θ)()(
j
*
j m
fmj
jL
mjmj
TttJt

+
+⋅= ττ
(55)
with
mj
J : j-motor inertia moment reflected to j-
motor axis [N · m · s
2
/ rad];
mj
θ

:
j-motor angular
acceleration referred to
j-motor axis [rad / s
2
];
fmj
T
:
friction torque generated in the
j-motor axis referred
to
j-motor axis [N · m];
mj
θ

:
j-motor angular velocity
referred to
j-motor axis [rad /s], with j = 1, 2, 3.
From eq. 55:
τ
L1
*
)(
1
1
11
NxTNxJx ··
227
fm
m
−− ⋅=

(56)
τ
L2
*
)(
2
2
22
NxTNxJx ··
448
fm
m
−− ⋅=

(57)
τ
L3
*
)(
3
3
33
NxTNxJx ··
669
fm
m
−− ⋅=

(58)
From eq. 52 to 54, and replacing eq. 56 to 58 in eqs.
46 to 51, the following state equation are obtained:
x

1
=
x
2
(59)
x

2
=
f
14
*
· ))((
1
1
11
NxTNxJx ··
227
fm
m
−− ⋅

+ f
23
*
+ f
15
*
·
2
22
fm
m
TNxJx
48
−− ⋅⋅

(
))(
2
Nx ·
4
+ f
24
*
+ f
16
*
· −
9
x(
6
xJ
3m

⋅
3
3
3
NxTN ··
6
fm
(− )) + f
25
*
(60)
x

3
=
x
4
(61)
x

4
=
f
17
*
·
))((
1
1
11
NxTNxJx ··
227
fm
m
−− ⋅

+ f
26
*
+ f
18
*
·
2
22
fm
m
TNxJx ·
48
−− ⋅

(
))(
2
Nx ·
4
+ f
27
*
+ f
19
*
· ·
69
xJx
3m

⋅
−(
3
3
3
NxTN ·
6
fm
(− )) + f
28
*
(62)
x

5
=
x
6
(63)
x

6
=
f
20
*
· ))((
1
1
11
N·xTN·xJx
227
fm
m
−− ⋅

+ f
29
*
+ f
21
*
· ⋅⋅−
48
xJx
2m

(
2
2
fm
TN −
))(
2
Nx ·
4
+ f
30
*
+ f
22
*
· ·
69
xJx
3m

⋅
−(
)(
3
3
3
NxTN ·
6
fm
− )+ f
31
*
(64)
x

7
=
[
k
a1
· v
a1
(t)
−
r
a1
· x
7
−
k
a1
· k
b1
(t) · x
2
·
N
1
] / L
a1
(65)
x

8
=
[
k
a2
· v
a2
(t)
−
r
a2
· x
8
−
k
a2
· k
b2
(t) · x
4
·N
2
] / L
a2
(66)
x

9
=
[
k
a3
· v
a3
(t)
−
r
a3
· x
9
−
k
a3
· k
b3
(t) · x
6
·
N
3
] / L
a3
(67)
5 CONTROLLER MODEL
The controller is modelled as:
V
a1
(t) =
−
k
1
· sgn(s
1
)
(68)
V
a2
(t) =
−
k
2
· sgn(s
2
)
(69)
V
a3
(t) =
−
k
3
· sgn(s
3
)
(70)
in which:
s
1
= w
1
· (x
1
- x
1d
) + x

1
(71)
s
2
= w
2
· (x
2
- x
3d
) + x

2
(72)
s
3
= w
3
· (x
3
- x
3d
) + x

3
(73)
where
k
j
: j-discontinuity gain [V]; s
j
: j-sliding
surface [rad
/ s] ; w
j
: j-position gain [1 / s]; with j = 1,
2, 3.
6 SIMULATIONS RESULTS
In these simulations the specified changes in
revolution joint angles are sinusoidal signals:
Table 1: References trajectories.
Joint
Amplitude [rad] Frequency [rad /s]
x
1
π /3 3 π /5
x
3
π /4
π
x
5
1 0
The given initial conditions were [
x
1
(0)
x
2
(0)
x
3
(0)
x
4
(0)
x
5
(0)
x
6
(0)
x
7
(0)
x
8
(0)
x
9
(0) ]
T
=
[0 0 0 0 0 0 0 0 0]
T
; the required torque to be
delivered by the actuators was determined.
When usually neglected nonlinearities are
considered, for certain system parameters (see
appendix), chaotic behavior was detected in the end-
of-arm, just as it is presented in the figures 1 and 2.
Figure 1: Last link position.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
74

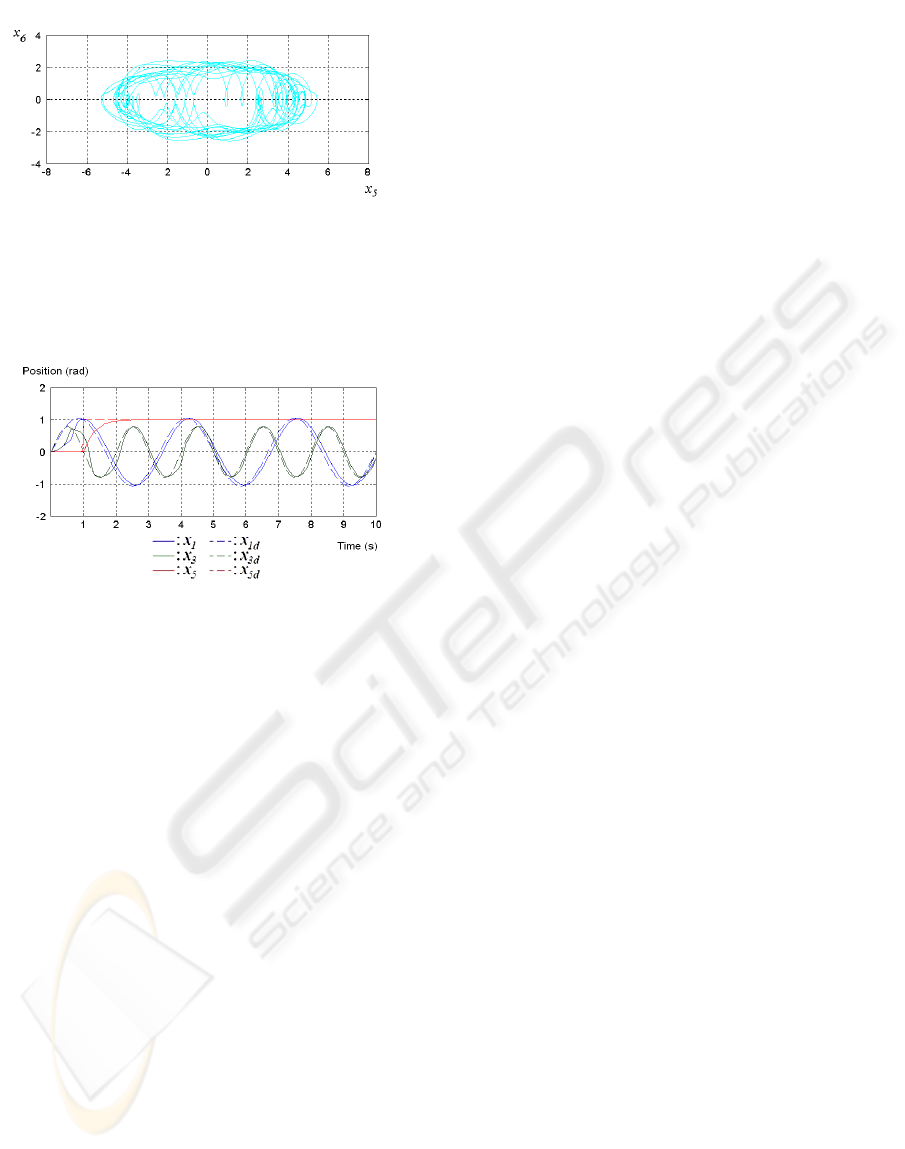
Figure 2: Phase plane (
x
5
, x

5
).
For every robot joint, a prescribed path is
considered. In
t = 1 [s] step response for the end-of-
arm is imposed; for the first and second link, in
t = 0
[s] sinusoidal signals are imposed (see figure 3).
Figure 3: Angular position of the links.
From figure 3, it is possible to appreciate that the
chaotic behavior was controlled and the desired
paths were tracked.
7 CONCLUSIONS
In this article, models are developed for the actuator
and manipulator that address some of the
nonlinearities usually neglected in current models.
The manipulator is placed in the same plane of
the action of the gravity force and effects such as
viscous, static and Coulomb friction in DC motors;
viscous, static and Coulomb friction in manipulator
joints; actuators and gear trains, are considered in
this dynamic model.
The controller design has allowed controlling the
detected chaotic behavior.
ACKNOWLEDGEMENTS
This work was possible thanks to the support of
DICYT – Universidad de Santiago de Chile,
USACH, through Project 060713UO and Project
060713JD.
REFERENCES
Zohdy, M., Fadali, M.S., Liu, J., 1992. Variable Structure
Control Using System Decomposition. IEEE Trans. on
Automatic Control. 37 (1514-1517)
Park, D., Choi, S., 1999. Moving Sliding Surfaces for
High-Order Variable Structure Systems. Int. J. of
Control. 72 (960-970)
Bartoszewicz, A., 1995. Sliding Modes for Fast Robot
Control. SAMS. 18-19 (539-542)
Xu, J., Lee, T.H., Wang, M., Yu, X., 1996. Design of
Variable Structure Controllers with Continuous
Switching Control. Int. J. of Control. 65 (409-431)
Lu, X., Spurgeon, S., 1999. Robustness of Static Sliding
Mode Control for Non-Linear Systems. Int. J. of
Control. 72 (1343-1353)
Chen, C., Xu, R., 1999. Tracking Control of Robot
Manipulator Using Sliding Mode Controller with
Performance Robustness. Trans. ASME J. Dyn. Syst.
Measurement Control. 121 (64-70)
Canudas, C., Aström, K., Braun, K., 1987. Adaptive
Friction Compensation in DC-Motor Drives. IEEE J.
of Robotics and Automation. RA-3 (681-685)
Kircanski, N., Goldenberg, A., 1997. An Experimental
Study of Nonlinear Stiffness, Hysteresis, and Friction
Effects in Robot Joints with Harmonic Drives and
Torque Sensors. Int. J. of Robotics Research. 16 (214-239)
Urrea, C., 1999. Control de Oscilaciones No Lineales en
un Manipulador de Dos Grados de Libertad, Tesis de
Magister en Ciencias de la Ingeniería, Universidad de
Santiago de Chile.
Leahy, M., Valavanis, K., Saridis, G., 1989. Evaluation of
Dynamic Models for PUMA Robot Control. IEEE
Trans. on Robotics and Automation. 5 (242-245)
Mahla, I., Urrea, C., 1999. Planar Robot Model Including
Driving, Nonlinear Friction and Cubic Stiffness.
Proceedings of the IASTED International Conference,
Philadelphia.
Craig, J., 1986. Introduction to Robotics: Mechanics and
Control. Addison-Wesley.
Hu, J., Dawson, D., 1996. Position Tracking Control for
Robot Manipulators Driven by Induction Motors
without Flux Measurements. IEEE Trans. on Robotics
and Automation. 12, (419-437)
Van Willigenburg, L., Loop, R., 1991. Computation of
Time-Optimal Controls Applied to Rigid
Manipulators. Int. J. Control. 47 (1097-1117)
Vukobratovic´, M., 1997. The Role of Environment
Dynamics in Contact Force Control of Manipulation
Robots. Trans. ASME J. Dyn. Syst. Measurement
Control. 119 (86-89)
APPENDIX
Simulation Parameters. The following parameter
values were taken from (Hu, J. and Dawson, D.,
1996), (Van Willigenburg, L. and Loop, R., 1991),
(Vukobratovic´, M., 1997).
DETECTION AND CONTROL OF NON-LINEAR BEHAVIOR BY SLIDING MODES CONTROL IN A 3 D.O.F.
ROBOT
75

Motors and their Reduction Gears
Manipulator
Link 1 Link 2 Link 3
m
1
9.86
m
2
6.38
m
3
3.21 3*
[Kg]
l
1
0.45
l
2
0.5
l
3
0.3
[m]
l
c1
0.3
l
c2
0.3243
l
c3
0.2 0.25*
[m]
I
1
1.1835
I
2
0.1371
I
3
0.0268
[Kg · m]
α
0
100
α
0
100
α
0
100
[N ·m]
α
1
1.01
α
1
1.01
α
1
1.01
[N ·m]
α
2
0.018
α
2
0.018
α
2
0.018
[N·m·s /rad]
v
0
0.01
v
0
0.01
v
0
0.01
[N·m·s /rad]
The manipulator parameter values that generated
chaotic behavior were denoted with
*. This chaotic
behavior was eliminated by the following parameter
values that we have proposed for the controllers.
Controllers
1. First Actuator (M1) Controller
k
1
260
[Volts]
w
1
10
[1
/ s ]
2. Second Actuator (M2) Controller
k
2
100
[Volts]
w
2
20
[1
/ s ]
3. Third Actuator (M3) Controller
k
3
200
[Volts]
w
3
3
[1
/ s ]
Motor M1 Motor M2 Motor M3
1a
L
0.0048
2a
L
0.0048
2a
L
0.0048
[H]
1a
R
1.6
2a
R
1.6
2a
R
1.6
[Ω]
1a
K
0.35
2a
K
0.35
2a
K
0.35
[N · m / A]
1b
K
0.04
2b
K
0.04
2b
K
0.04
V
olts·s / rad]
α
0
260
α
0
260
α
0
260
[N · m]
α
1
1.64
α
1
1.64
α
1
1.64
[N · m]
α
2
0.018
α
2
0.018
α
2
0.018
[N·
m· s /
rad]
v
0
0.01
v
0
0.01
v
0
0.01
[rad
/ s]
N
1
62.55
N
2
62.55
N
3
62.55
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
76