SENSOR AND ACTUATOR FAULT ANALYSIS IN ACTIVE

SUSPENSION IN VIEW OF FAULT-TOLERANT CONTROL

Claudio Urrea and Marcela Jamett

Departamento de Ingeniera El´ectrica, Av. Ecuador 3519, Est. Central, Santiago, Chile

Keywords:

Active suspension, sensor and actuator faults, full-vehicle suspension model.

Abstract:

This paper shows the ﬁrst step of a fault tolerant control system (FTCS) to control active suspension on a

full-car suspension model. In this paper, the elimination of the inevitable pitch and roll actions of a spring

suspension between each axle and the body of a vehicle is studied. An actuator (linear motor) producing an

electromagnetic force and a pneumatic force acting simultaneously on the same output element is used. This

linear motor acts as a force generator that compensates instantly for the disturbing effects of the road surface.

Simulation results to illustrate the system’s performance in front of the occurrence of sensor and actuator faults

are shown.

1 INTRODUCTION

Vehicle suspension systems have developed over the

last 100 years to a very high level of sophistication

(Buckner, Schuetze, and Beno, 2000; Fukao, Ya-

mawaki, and Adachi, 2000). Most vehicle today use

a passive suspension system employing some type of

springs in combination with hydraulic or pneumatic

shock absorbers, and linkages with tailored ﬂexibility

in various directions. These suspension system de-

signs are mostly based on ride analysis.

Traditionally automotive suspension designs have

been a compromise between the three conﬂicting cri-

teria of road holding, load carrying and passenger

comfort. In fact, despite the wide range of designs

currently available by using passive components, we

can only offer a compromise between these conﬂict-

ing criteria by providing spring and damping coefﬁ-

cients with ﬁxed rates

On the other hand, active suspensions have been

extensively studied in the last three decades (Giua,

Seatzu, and Usai, 2000; Lefebvre, Chevrel,and

Richard, 2001; Lakehal-Ayat, Diop, and Fe-

naux,2002). In an active suspension the interaction

between vehicle body and wheel is regulated by an

actuator of variable length capable of supplying the

entire control force system’s requirements.

Ride comfort in ground vehicles usually depends

Components for passive suspension can only store and

dissipate energy in a pre-determined manner.

on a combination of vertical motion (heave) and an-

gular motion (pitch and roll). Active suspension is

characterized by a built-in actuator which can gen-

erate control forces to suppress the above mentioned

roll and pitch motions.

Including the dynamics of the hydraulic system

consisting of ﬂuids, valves, pumps, etc., complicates

the active suspension control problem even further

since it introduces nonlinearities to the system. It

has been noted that the hydraulic dynamics and fast

servo-valve dynamics make controls design very dif-

ﬁcult (Karlsson, Teely, and Hrovatz, 2001; Alleyne,

and Hedrick, 1995). The actuator dynamics signif-

icantly change the vibrational characteristics of the

vehicle system (Engelman, and Rizzon, 1993). Us-

ing a force control loop to compensate for the hy-

draulic dynamics can destabilize the system (Alleyne,

Liu, and Wright, 1998). This full nonlinear control

problem of active suspensions has been investigated

using several approaches including optimal control

based on a linearized model (Engelman, and Riz-

zon, 1993), adaptive nonlinear control (Alleyne, and

Hedrick, 1995), and adaptive control using backstep-

ping (Karlsson, Teely, and Hrovatz, 2001). These

schemes use linear approximations for the hydraulic

dynamics or they neglect the servo-valve model dy-

namics in which a current or voltage is what ulti-

mately controls the opening of the valve to allow ﬂow

of hydraulic ﬂuid to or from the suspension system.

However, nowadays a novel family of highly dynamic

electro-magnetic direct drives exit, i.e. servomotors

179

Urrea C. and Jamett M. (2008).

SENSOR AND ACTUATOR FAULT ANALYSIS IN ACTIVE SUSPENSION IN VIEW OF FAULT-TOLERANT CONTROL.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 179-186

DOI: 10.5220/0001490201790186

 SciTePress

that looks like a hydraulic piston with acceleration

rates of over 200 [m/s

] make cyclic movement at

several Hertz possible.

Active suspension control systems reduce undesir-

able effects by isolating car body motion from vibra-

tions at the wheels, but their componentfailures/faults

are inevitable and unpredictable, and without care-

ful and prompt treatment, they tend to develop into

the severe total failure of the whole system. Conti-

nued operation of these systems has both economic

and safety implications. Every mechanical system is

vulnerable to faults that can lead to failure of the com-

plete system, unless mitigating strategies are included

at the design stage (Noura, Theilliol, and Sauter,

2000). Control element failures not only degrade the

performance of control systems, but also may intro-

duce instability and thus can cause serious operation

and safety problems. Therefore, fault tolerance has

been one of the major issues in process control.

In automated systems, the goal of the fault-

tolerance is to continue operation in spite of failures,

if this is possible. A general problem has been that

fault conditions could not be treated as an integrated

part of system design. Therefore, automated systems

to provide uninterrupted service, even in the presence

of failures are required (Zhang, Jiang, 2002).

Most of the past work uses the quarter-car model,

which includes only two degree-of-freedomof the ve-

hicle motion in the vertical direction (Lakehal-Ayat,

Diop, and Fenaux,2002). In general, the heave, pitch

and roll motions are coupled and an impulse at the

front or rear wheels excites all three motions. This

means that pitch-, heave- and roll-controllers can-

not be independently designed. Therefore, we take

a model based in (Ikenaga, Lewis, Campos, Davis,

2000) including the full vehicle suspension dynamics

considering heave, pitch and roll motions.

The paper is organized as follows: in section 2 the

system description is given. In section 3, the state-

space model for the full-vehicle suspension model is

presented. In section 4, the vehicle controller is de-

veloped. Section 5 presents fault analysis and some

simulation results. Finally, in section 6, the conclu-

sions and outline future work are discussed.

2 SYSTEM DESCRIPTION

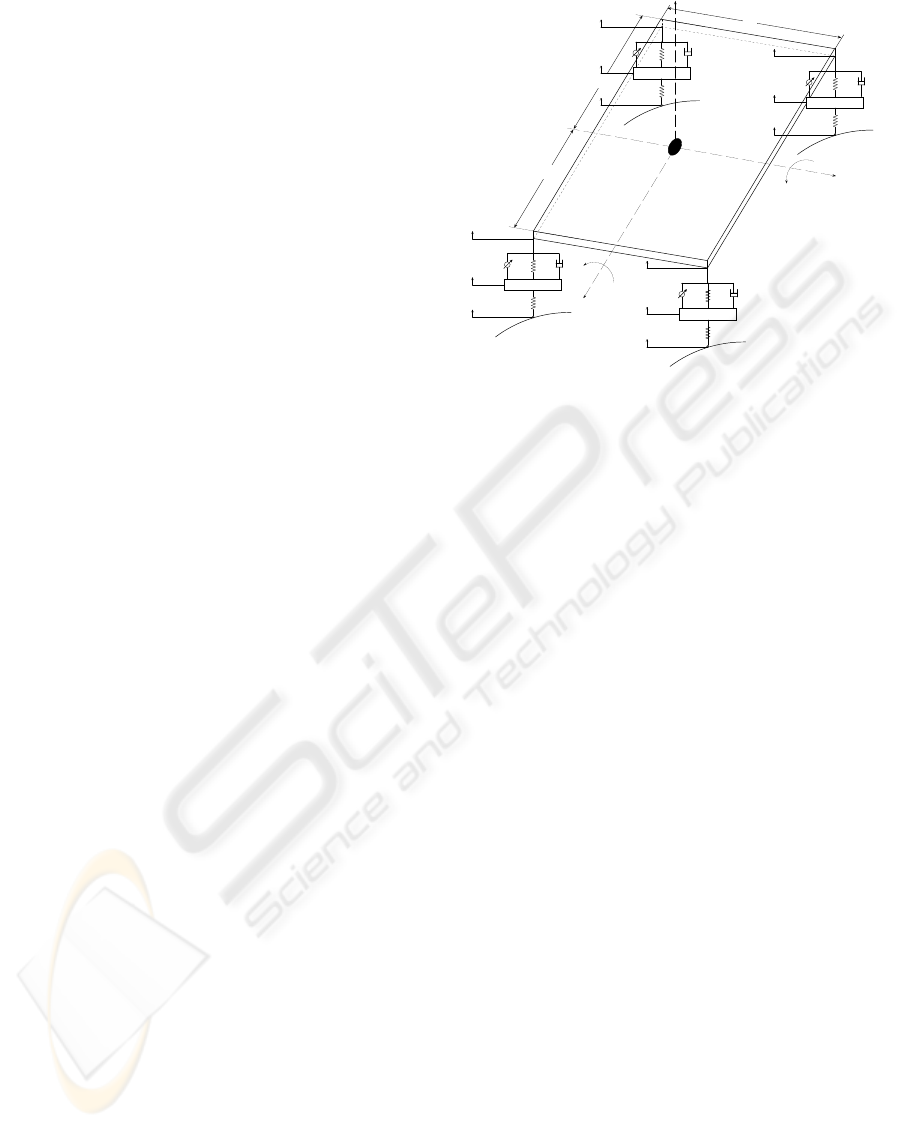
2.1 Full-Vehicle Suspension Model

(Seven DOF System)

In this work, a full-vehicle suspension mathematical

model depicted in Fig.1 is considered.

Figure 1: Full-vehicle suspension model.

where the followings parameters and variables are

taken which respect to the static equilibrium position

(Ikenaga, Lewis, Campos, Davis, 2000):

• ms is sprung mass [kg],

• mu is unsprung mass [kg],

• Ks

is front-left suspension spring stiffness

[N/m],

• Ks

is front-right suspension spring stiffness

[N/m],

• Ks

frl

is rear-left suspension spring stiffness

[N/m],

• Ks

is rear-right suspension spring stiffness

[N/m],

• Bs

is front-left suspension damping [N/m/s],

• Bs

is front-right suspension damping [N/m/s],

• Bs

frl

is rear-left suspension damping [N/m/s],

• Bs

is rear-right suspension damping [N/m/s],

• Ku

is tire-left spring stiffness [N/m],

• Ku

is tire-right spring stiffness [N/m],

• Ku

frl

is tire-left spring stiffness [N/m],

• Ku

is tire-right spring stiffness [N/m],

• a is length between front of vehicle and center of

gravity of sprung mass [m],

• b is length between rear of vehicle and center of

gravity of sprung mass [m],

• w is width of sprung mass [m],

• I

is roll axis moment of inertia [kg · m

• I

is pitch axis moment of inertia [kg · m

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

180

• F

is force at the front-left suspension [N],

• F

is force at the front-right suspension [N],

• F

is force at the rear-left suspension [N],

• F

is force at the rear-right suspension [N],

• Zr

is terrain disturbance heights at the front-left

wheel [m],

• Zr

is terrain disturbance heights at the front-

right wheel [m],

• Zr

is terrain disturbance heights at the rear-left

wheel [m],

• Zr

is terrain disturbance heights at the rear-right

wheel [m],

• g is the constant of graveness in the terrestrial sur-

face, 9.80665 [m/s

In this model, the car body is represented as a

sprung mass, and the wheels are represented as an

unsprung mass connected to the ground via the tire

spring. The tire is an undamped spring between the

axle and the ground. The suspension consists of pas-

sive dampers in parallel with four actuators and four

springs.

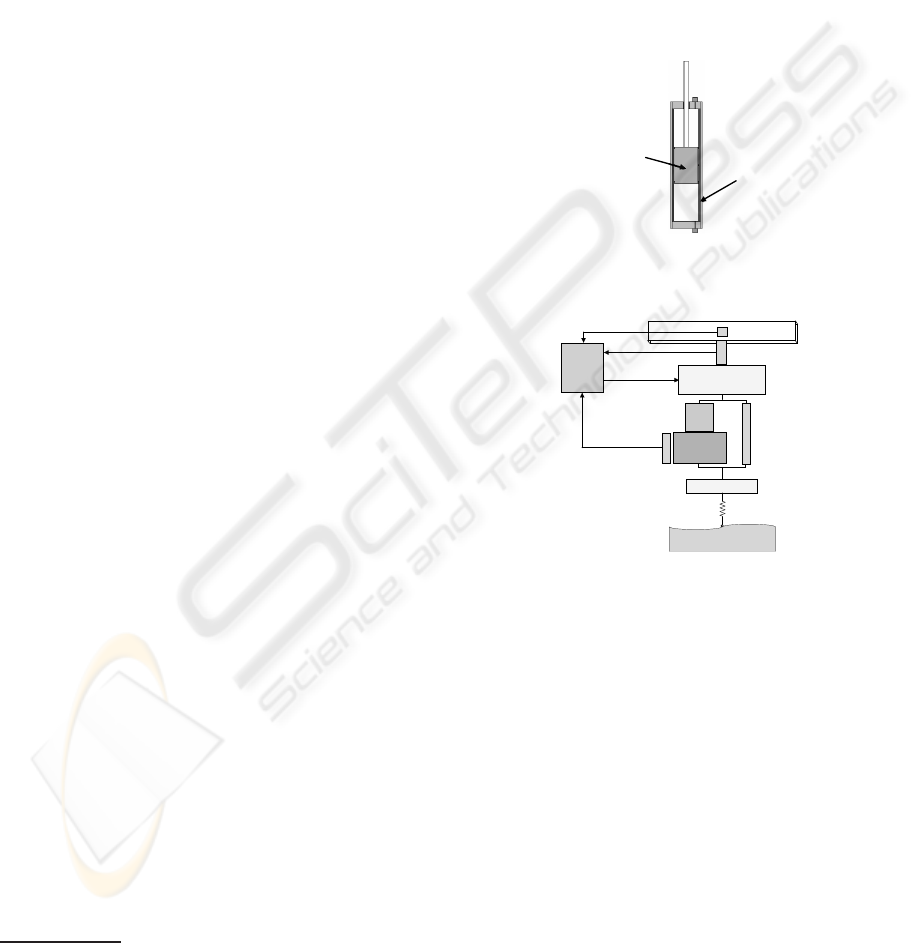
2.2 Actuators

The suspension actuators are taken to be a force actu-

ator acting between the car body and the axle of the

car. The chosen ServoRam

TM2

actuator, depicted in

Fig. 2, produces an electromagnetic force and a pneu-

matic force acting simultaneously on the same output

element. This electromagnetic actuator has zero me-

chanical hysteresis, since the force is applied directly

to the output element. It has zero electrical hystere-

sis because a microamp in one direction produces a

positive force, and a microamp in the opposite direc-

tion produces a negative force, so that the force output

is an exactly linear function of the current input. A

linear transducer measures the position of the piston.

The small control time constant allows the force to

be changed at a rate of thousands of Newtons per mil-

lisecond, so the suspension system can instantly adapt

to every road condition. These linear motors consists

of just two parts: the ﬁxed stator and the moveable

slider. These two parts are not connected by slip rings

or by cables. Since the linear stroke directly with-

out the use of mechanical gears, belts or ball screws,

there is no wear or mechanical play. In a practical

point of view, the ram is placed between the wheel

Name applied to the AMTr ram technology, and all

AMTr electromagnetic rams are, in fact, ServoRam

This technology has been developed over the last 10 years

by AMT’s Chief Scientist, Phillip Denne.

point (on the vehicle chassis) and the wheel stub axle,

so as to carry all the vertical forces, see Fig. 3. The

forces transferred from the wheel to the chassis may

be precisely controlled by the electromagnetic forces.

A force-measuring transducer may be used to control

the current to the coil system, so as to maintain the

total upward force at a constant value, irrespective of

the wheel vertical motion. The desired value of this

constant force may be determined in turn by the out-

put from a wheel-point accelerometer, so as to hold

the vehicle steady against pitch and roll motions, for

example.

Magnet array on moving

armature/piston

Coil array on fixed

stator/cylinder

Figure 2: Simpliﬁed schematic of the ServoRam

actua-

tor.

Ground

Electromagnetic

forces

Acceleremeter

Correction

Force

control

loop

force transducer

Ram position

transducer

friction

Suspension

mass

Air

Spring

Figure 3: ServoRam

actuator system for active suspen-

sion.

3 STATE SPACE-MODEL

The governing equations of this system are presented

considering the following state variables (Ikenaga,

Lewis, Campos, Davis, 2000):

• x

= z is the heave position (ride height of sprung

mass),

• x

= ˙z is the heave velocity (payload velocity of

sprung mass),

• x

= θ is the pitch angle,

• x

θ is the pitch angular velocity,

• x

= φ is the roll angle,

• x

φ is the roll angular velocity,

SENSOR AND ACTUATOR FAULT ANALYSIS IN ACTIVE SUSPENSION IN VIEW OF FAULT-TOLERANT

CONTROL

181

• x

= Zu

is the front-left wheel unsprung mass

height,

• x

is the front-left wheel unsprung mass

velocity,

• x

= Zu

is the front-right wheel unsprung mass

height,

• x

is the front-right wheel unsprung mass

velocity,

• x

= Zu

is the rear-left wheel unsprung mass

height,

• x

is the rear-left wheel unsprung mass

velocity,

• x

= Zu

is the rear-right wheel unsprung mass

height,

• x

is the rear-right wheel unsprung mass

velocity,

Linear differential equations that describe the dynam-

ics can be formulated as:

˙x

= x

˙x

= (F

+ F

− (Ks

+ Ks

+Ks

) · x

− (Bs

+ Bs

) · x

+(a· (Ks

+ Ks

) − b· (Ks

+ Ks

))x

(a· (Bs

+ Bs

) − b· (Bs

+ Bs

)) · x

· x

+ Bs

· x

+ Ks

· x

+ Bs

· x

+ Bs

· x

+ Ks

· x

+ Bs

· x

)

/ms− g

˙x

= x

˙x

= (−a· (F

+ F

) + b· (F

+ F

) + (a· (Ks

+ Ks

) − b· (Ks

+ Ks

)) · x

+ (a· (Bs

+ Bs

) − b· (Bs

+ Bs

)) · x

− (a

· (Ks

+Ks

) + b

· (Ks

+ Ks

)) · x

− (a

· (

+ Bs

) + b

· Bs

+ Bs

)) · (x

− a·

· x

− a· Bs

· x

− a· Ks

· x

− a·

· x

+ b· Ks

· x

+ b· Bs

· x

+ b·

· x

+ b· Bs

· x

)/I

(1)

˙x

= x

˙x

= ((F

− F

+ F

− F

) −

· ((Ks

+ Ks

) · x

+ (Bs

+ Bs

)) · x

+ Ks

· x

+ Bs

· x

− Ks

· x

−Bs

· x

+ Ks

· x

+ Bs

· x

− Ks

+ Bs

· x

)/(2· w/I

)

˙x

= x

˙x

= x

˙x

= (−F

+ Ks

· x

+ Bs

· x

− a· Ks

· x

−a· Bs

· x

−

· Ks

· x

−

· Bs

· x

−(Ku

+ Ks

) · x

− Bs

· x

+ Ku

)/mu

− g

˙x

= x

˙x

= (−F

+ Ks

· x

+ Bs

· x

+ b· Ks

· x

b· Bs

· x

· Ks

· x

· Bs

· x

−

(Ku

+ Ks

) · x

− Bs

· x

+ Ku

· Zr

)

/mu

− g

˙x

= x

˙x

= (−F

+ Ks

· x

+ Bs

· x

+ b· Ks

· x

b· Bs

· x

−

· Ks

· x

−

· Bs

· x

−

(Ku

+ Ks

) · x

− Bs

· x

+ Ku

· Zr

)

/mu

− g (2)

This system can be summarized by the following lin-

ear space-state representation:

˙x(t) = A· x(t) + B· u(t) + B

· u

(t)

y(t) = C· x(t), (3)

where:

• x ∈ ℜ

14x1

is the system state vector,

• u ∈ ℜ

4x1

is a vector composed of the control

forces. u = [F

]

• u

∈ ℜ

5x1

is a vector whose components are the

disturbance inputs. u

= [g Zr

]

• y ∈ ℜ

3x1

is the system output vector. y = [Z θ ϕ]

• A,B,B

,and C are constant matrices of appropri-

ate dimensions.

4 CONTROLLER MODEL

The controller design considers:

• Control loops that stabilize heave, pitch and roll

responses,

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

182

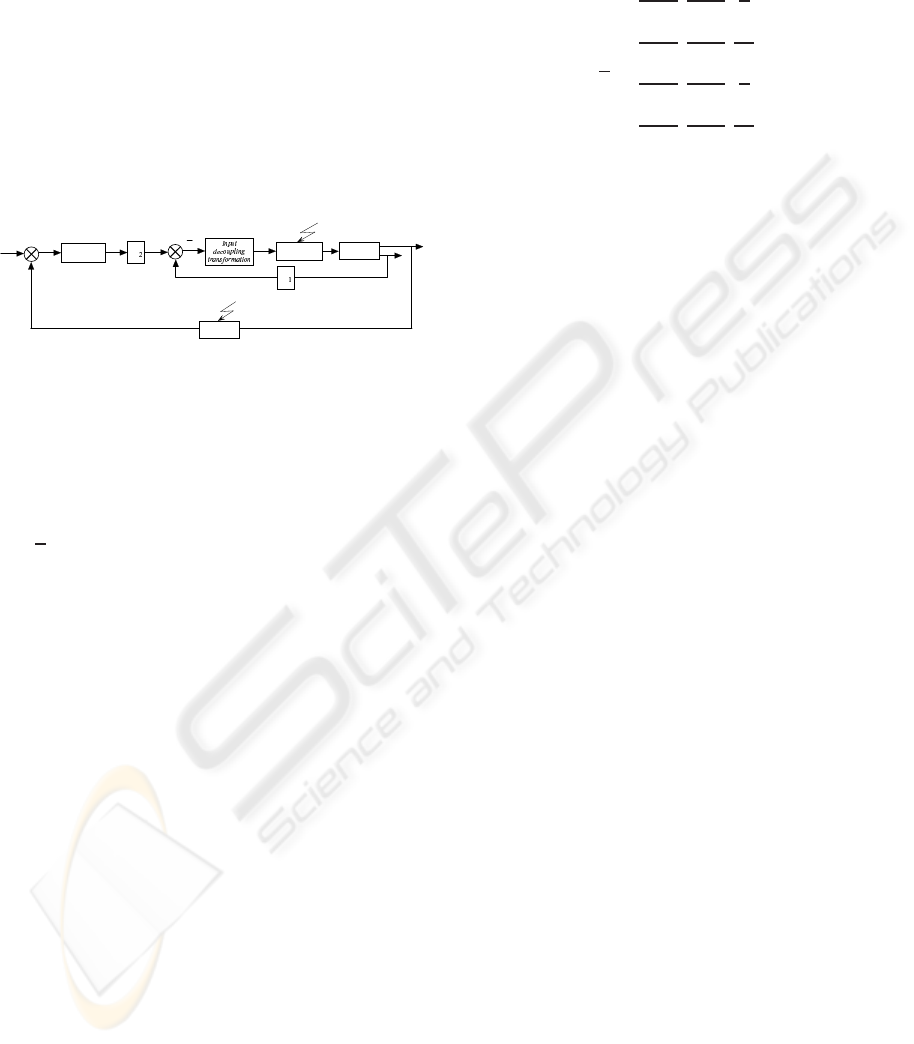
• Input decoupling transformation that blends the

inner and outer control loops allowing stream-

lined design yet gives performance better than

over-simpliﬁed decoupled techniques.

By employing a state observer, the full state feed-

back is available for the entire vehicle, and pitch an-

gle is inferred from a combination of rate sensors and

accelerometers. The control law ¯u is computed by

a state feedback associated with the integral of the

tracking error: ¯u = - [K

] · [x q]

= - K · ¯x; K

and

are computed according to Eq.4. This controller

design is illustrated in Fig.4.

Fault

System

- K

Integrator

Sensors

Fault

Actuators

- K

Figure 4: Controller block diagram.

The control procedure can be brieﬂy summarized

as follows: Let us consider the followingoptimization

problem.

The performance index to be minimized is:

J =

∞

[ ¯x

(t) · Q· ¯x(t) + ¯u

(t) · R· ¯u(t)]dt, (4)

where:

• ¯x ∈ ℜ

17x1

is the augmented system state vector. ¯x

= [x

]

• ¯u ∈ ℜ

3x1

is a vector whose components are the

control forces, provided by the actuators, for

heave (F

), pitch (F

) and roll (F

• Q ∈ ℜ

17x17

is positive semi-deﬁnite matrix,

• R ∈ ℜ

3x3

is tuning diagonal matrix.

The good performance of the suspension system

is related to the minimization of the term ¯x

·Q· ¯x and

an adequate choice of R, because the comfort depends

of the term ¯u

·R· ¯u. The optimal control strategy that

minimizes the cost function was found to be ¯u(t) =

- K· ¯x(t), where the gain matrix Kcan be computed

by solving an algebraic Riccati equation. So, a set

of LQR optimal feedback gains corresponding to dif-

ferent weighting factors in the quadratic function J is

chosen. The feedback control is designed to increase

the relative damping of a particular mode of motion

in the system by augmenting one or more of the co-

efﬁcients of the equation of motion by actuating the

control signals in response to motion feedback vari-

ables.

From Fig.1, the equivalent relationship between

(t), F

(t) and F

(t), and the forces generated by the

actuators can be deﬁned by:







(t)













(a+b)

−1

(a+b)

−1

(a+b)

−1

(a+b)

−1













(t)







(5)

Therefore the nominal control is given by:







(t)







= − K · ¯x(t), (6)

where K ∈ ℜ

3x17

5 FAULT ANALYSIS AND

SIMULATION RESULTS

In the following simulations, the full-car suspension

system was simulated for the input terrain distur-

bances Zr(t) actuating between 2 ≤ t ≤ 8 s:

Zr(t) =







(t)













0.05· sin(w·t)

0.15· sin(w·t)

0.05· sin(w· (t +τ))

0.15· sin(w· (t +τ))







, (7)

where:

• ω = 9 [rad/s], is the terrain disturbance frequency,

• τ = 0.1409 [s], is the time delay given by: τ = L/v

= (a+ b)/v,

• L is the distance between the front and rear axles

of the vehicle [m],

• v = 22 [m/s], is the speed at which the vehicle

travels.

The given initial conditions are ¯x = 0, and the re-

quired torque to be delivered by the actuators is deter-

mined as in fault-free cases. The objective here is to

analyze the effects of a sensor- and actuator-faults on

the active suspension.

5.1 Sensor Fault

At t = 5.5 s a sensor fault occurs in the second sensor

measuring θ. This fault corresponds to a bias equal

SENSOR AND ACTUATOR FAULT ANALYSIS IN ACTIVE SUSPENSION IN VIEW OF FAULT-TOLERANT

CONTROL

183

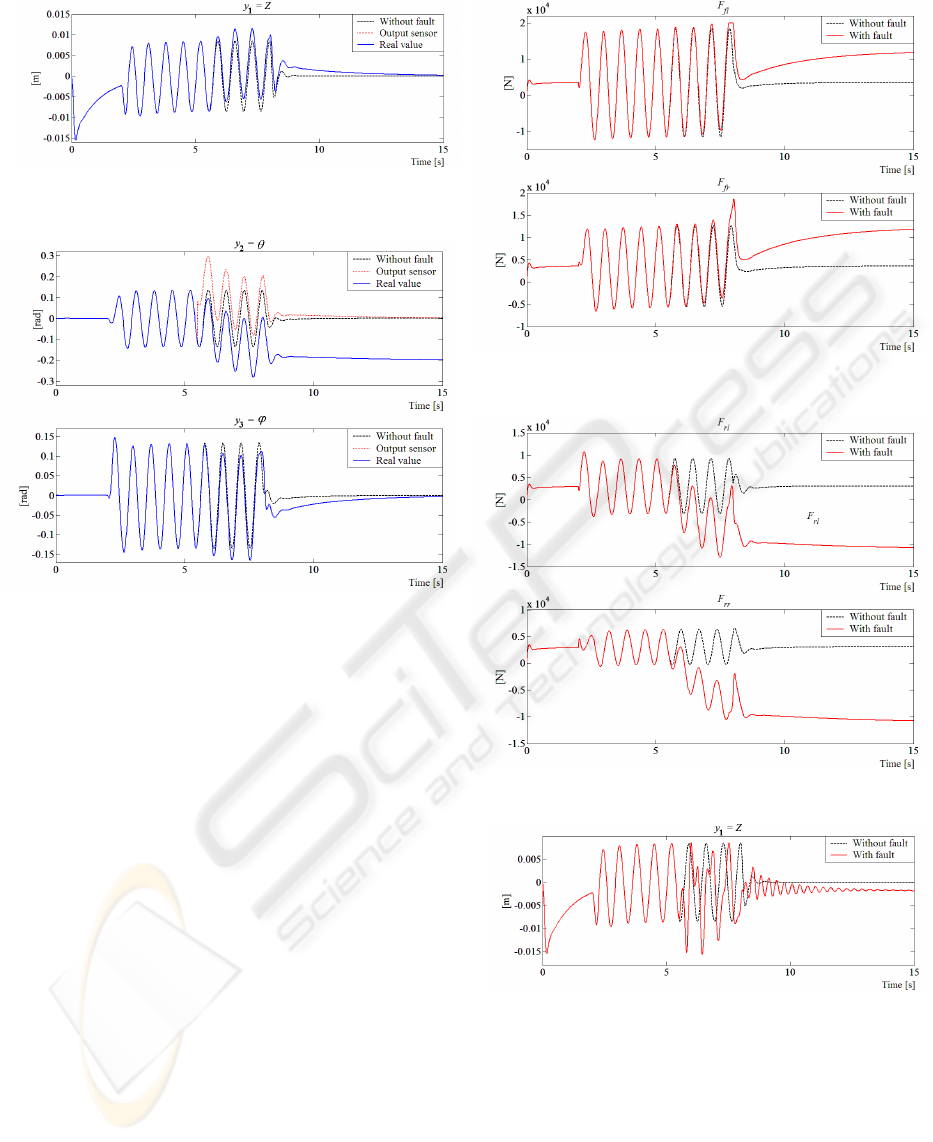
Figure 5: y

: Heave position (ride height of sprung mass).

Figure 6: (a) y

: Pitch angle; (b) y

: Roll angle.

to 0.2 rad. Due to this fault, similar real value θ is

shifted of - 0.2 rad from the output sensor which goes

to its reference value. The real value of θ is far from

its reference because the control input naturally reacts

in the presence of the sensor fault. Figs. 5 and 6 show

that the other outputs Z and ϕ are also affected by this

fault but reach their reference value again.

The increase of the necessary force that should be

applied to the actuators in front of this default is de-

picted in Figs. 7 and 8. Fig. 7(a) illustrates a satu-

ration (± 20000 [N]) reached in the actuator, in the

presence of this fault. Figs. 7(b) and 8 show the other

inﬂuence of this sensor fault on the control input.

5.2 Actuator Fault

Other experiments simulating actuator faults are per-

formed. At t = 5.5 [s], a reduction of 75% in the se-

cond actuator effectiveness (F

) is simulated. Figs.

9 to 12. illustrate simulation results. Figs. 9 and 10

show the permanent shift between the outputs with

no fault and the outputs with fault. This shift is due

to the fact that the other control inputs are affected by

the fault due to the closed-loop and coupling between

each other.The new necessary forces that should be

applied in the actuators to compensate this loss of

Figure 7: (a) F

: Force at the front-left suspension; (b) F

Force at the front-right suspension.

Figure 8: (a) F

: Force at the rear-left suspension; (b) F

Force at the rear-right suspension.

Figure 9: y

: Heave position (ride height of sprung mass).

effectiveness are shown in Figs. 11 and 12. These

force increases do not surpass the maximum allow-

able force limits in the actuators.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

184

Figure 10: (a) y

: Pitch angle; (b) y

: Roll angle.

Figure 11: (a) F

: Force at the front-left suspension; (b)

: Force at the front-right suspension.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, it was shown that active suspension can

improve all three performance aspects i.e. passenger

ride comfort, handling, and rattle space.

A nominal control law is designed for this active

suspension system and the effect of the proﬁle of the

road is analyzed in the ﬁrst part. The main aim of

this work is the study of the inﬂuence of sensor and

actuator faults on the control law.

The obtained results are realistic and show the im-

portance of the design of a fault tolerant control sys-

tem (FTCS) able to compensate this kind of fault.

This work is just starting. Future work will also take

into account the loss of a complete sensor or actuator

in order to preserve safety and passengers’ comfort.

Figure 12: (a) F

: Force at the rear-left suspension; (b) F

Force at the rear-right suspension.

ACKNOWLEDGEMENTS

This work was possible thanks to the support of DI-

CYT – Universidad de Santiago de Chile, USACH,

through Project 0607UO and Project 0607JD.

REFERENCES

Buckner G., Schuetze K., Beno J.: Active Vehicle Suspen-

sion Control Using Intelligent Feedback Lineariza-

tion. American Control Conference, Chicago, Illinois,

USA (2000) 4019–4024

Fukao T., Yamawaki A., Adachi N.: Nonlinear and H

∞

Con-

trol of Active Suspension Systems with Hydraulic Ac-

tuators. American Control Conference, Chicago, Illi-

nois, USA (2000) 5125–5128

Giua A., Seatzu C., Usai G.: ActiveAxletree Suspension for

Road Vehicles with Gain-Switching. 39th IEEE Con-

ference on Decision and Control Sydney Convention

and Exhibition Centre, Sydney, Australia (2000)

Lefebvre D., Chevrel P.,Richard S.: A Hinﬁnity-based con-

trol design methodology dedicated to active control of

vehicle longitudinal oscillations. 40th IEEE Confer-

ence on Decision and Control Orlando, Florida, USA

(2001) 99–104

Lakehal-Ayat M., Diop S., Fenaux E.: Development of a

Full Active Suspension System. 15th Triennial World

Congress IFAC, Barcelona, Spain (2002)

Karlsson N., Teely A., Hrovatz D.: A Backstepping Ap-

proach to Control of Active Suspensions. 40th IEEE

Conference on Decision and Control Orlando, Florida,

USA (2001) 4170–175

Alleyne A., Hedrick J.: Nonlinear Adaptive Control of Ac-

tive Suspensions. IEEE Trans. Control Syst. Technol.

1 (1995) 94–101

SENSOR AND ACTUATOR FAULT ANALYSIS IN ACTIVE SUSPENSION IN VIEW OF FAULT-TOLERANT

CONTROL

185

Engelman G., Rizzon G.: Including the Force Generation

Process in Active Suspension Control Formulation.

American Control Conference, San Francisco, Cali-

fornia, USA (1993)

Alleyne A., Liu R., Wright H.: On the Limitations of

Force Tracking Control for Hydraulic Active Suspen-

sions. American Control Conference, Philadelphia,

USA (1998) 43–47

Noura H., Theilliol D., Sauter D.: Actuator Fault-Tolerant

Control Design: Demostration on a Three-Tank-

System. International Journal of Systems Science se-

ries 9 (2000) 1143–1155

Zhang Y., Jiang J.: Design of Restructurable Active

Faut-Tolerant Control Systems. 15th Triennial World

Congress IFAC, Barcelona, Spain (2002)

Ikenaga S., F. Lewis, Campos J., Davis L.: Active

Suspension Control of Ground Vehicle Based on a

Full-Vehicle Model. American Control Conference,

Chicago, Illinois, USA (2000) 4019–4024

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

186