
STABLE STATES TRANSITION APPROACH
A New Strategy for Walking Robots Control in Uncertain Environments
*
Anca Petrişor,
**
Nicu George Bîzdoacă,
*
Adrian Drighiciu
*
Faculty of Electromechanical Engineering, University of Craiova, Romania
**
Ilie Diaconu,
*
Sonia Degeratu,
**
Gabriela Canureci,
*
Gabriela Petropol Serb
**
Faculty of Automation,Computers and Electronics, University of Craiova, Romania
Keywords: Walking robot, mathematical model, control strategy, variable causality dynamic system, uncertain
environment.
Abstract: A new strategy for walking robots control in uncertain environments, called Stable States Transition
Approach (SSTA), is proposed in this paper. All the controls, both the steps succession and the evolution
inside each step are established by the evolution environment and by the objective proposed during the
evolution. There are no predetermined types of legs movements; they are on-line determined during the
robot evolution, irrespective of the ground shape. To apply this strategy it was necessary the robot
interpretation as a Variable Causality Dynamic Systems (VCDS). Experimental results are implemented and
verified in RoPa, a platform for simulation and design of walking robot control algorithms, to demonstrate
the efficacy of the proposed control method.
1 INTRODUCTION
In the last years, many researches combine results
from the fields of robotics and control systems,
especially for wheeled and legged mobile robots
(Fulgenzi, Spalanzani and Laugier, 2007), (Jung,
Hsia and Bonitz, 2004).
Mobile robots control in uncertain environments
represents still a challenge for real world
applications. The robot should be able to gain its
goal position facing the implicit uncertainty of the
surrounding environment.
The walking robots, particularly the legged
robots, allow many advantages with respect to the
wheeled robots, especially regarding the autonomy
in difficult environments. Unfortunately, a specific
type of movement called legged locomotion,
(Thirion 2001), (Cubero 2001), is characterized by
strongly nonlinear mathematical models to allow
describing both the fundamental aspects: leg
movements and leg coordination. During the legged
locomotion, the control algorithms must assure a
stable movement that can be dynamic stable
movement or static stable movement.
The problem of walking robots control in
uncertain environments has been deeply studied in
literature and several techniques have been
developed.
Many control algorithms implemented on the
existing walking robots, (CWR, 2003), are based on
"state of the art" technologies to control the
movements of articulated limbs and joint actuators.
Some of them try to recreate movements of
biological insects which execute various types of
periodic gait patterns and adaptive gaits at very high
speed, (Cubero, 2003). The walking control
algorithms are often around some distributed
architectures, (Schmucker, 1996), (Galt, 1999), by
assembling a multitude of small processes which are
executed concurrently.
Other approaches consider the robot having the
necessary intelligence to operate in uncertain
environments and use fuzzy logic or neural networks
based techniques, (Thirion, 2001), (Gu 2001),
(Nanayakkara, Watanabe, Izumi, and Kiguchi,
2001), advanced control schemas, genetic algorithms
(Kiguchi, Watanabe, Izumi, and Fukuda, 2000),
(Kumarawadu, Watanabe, Kiguchi and Izumi, 2002)
etc., to develop the dynamic walking.
202
Petri¸sor A., George Bîzdoac
ˇ
a N., Drighiciu A., Diaconu I., Degeratu S., Canureci G. and Petropol Serb G. (2008).
STABLE STATES TRANSITION APPROACH - A New Strategy for Walking Robots Control in Uncertain Environments.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 202-207
DOI: 10.5220/0001490302020207
Copyright
c
SciTePress

In this paper it is developed a new concept of
walking called SSTA "Stable States Transition
Approach" based on the variable causality
mathematical model of the walking robot. According
SSTA both the leg coordination and individual leg
movements are entirely dependent on the robot goal
and the environments only.
The control structure of SSTA, presented in this
paper, is proposed in order to apply the best control
with respect to safety issues and convergence to the
goal.
Simulation results show how the developed
walking control algorithm allows the robot to
navigate safely, in uncertain environments, toward
the goal and to modify its behavior according to the
SSTA control strategy.
The paper is structured as follows: in Section II
the geometrical structure of the walking robot is
described in detail; in Section III the variable
causality mathematical model of the walking robot is
described and discussed. In Section IV the general
block diagram of SSTA walking robot control is
proposed. In Section V the algorithm for walking
robot control in SSTA strategy is presented. In
Section VI simulation results are shown and
discussed. Last section closes the paper with
conclusions and purposes for future activities.
2 GEOMETRICAL STRUCTURE
OF THE WALKING ROBOT
It is considered the walking robot structure as
depicted in Fig.1, having three normal legs
ijp
L,L,L and a head equivalent to another leg, L
0,
containing the robot centre of gravity, G, placed in
its foot. The robot body RB is characterized by two
position vectors O
0
, O
1
and the leg joining points
denoted R
i
, R
j
, R
p
. The joining point of the head, L
0
,
is the central point O
0
, R
0
= O
0
, so the robot body RB
is univocally characterized by the set,
01ijp0
RB {O ,O , , , , }=λλλλ
(1)
where
0
0λ= .
The robot position in the vertical plane is defined
by the pair of the position vectors O
0
, O
1
where
10
|O O | 1−=, or by the vector O
0
and the scalar θ,
the angular direction of the robot body.
Figure 1: Geometrical structure of the robot.
The robot has a rigid body if the three scalars
(
i
,i 1:4λ= ) are time constant. The variable θ
determines the robot body angle in vertical plane.
The geometrical structure of the walking robot is
defined by the relations
10j
OO e
⋅θ
−=
(2)
k0kj
RO e
⋅θ
=
+λ ⋅
(3)
from which,
12 12
kk kk
j
12
RR ( )e,k,k{1,2,3,4}
⋅θ
−=λ−λ⋅ ∈
(4)
The robot position in the vertical plane is defined
by the pair of the position vectors O
0
, O
1
, where
10
|O O | 1
−
=
(5)
or by the vector O
0
and the scalar θ, the angular
direction of the robot body.
Each of the four robot legs L
k
, k=1:4 is
characterized by an Existence Relation ER(L)
depending on specific variables,
k
ER(L ) :
kkk
RGA0
−
−=
(6)
k1,k2,k
kkj kjju ju
Aae aee e
⋅α ⋅θ ⋅ ⋅
=⋅ =−⋅ ⋅ ⋅
(7)
k2,k
kkj kjju
Bbe bee
⋅β ⋅θ ⋅
=⋅ =−⋅ ⋅
(8)
kkj k
RGeAB0
⋅θ
−
+⋅ =
(9)
2,k 1,k
kjukkju
AB e [b a e ]
⋅⋅
=− + ⋅
(10)
From this point of view, the walking robot is an
object containing five fundamental components,
1234
WR {L ,L ,L ,L ,RB}
=
(11)
This determines a system of equations where the
unknown variables selection depends on the robot
status. This system is called Existence Relation of
the walking robot denoted ER(WR).
This means that in specific circumstances some
variables are effects of the others but the causality
ordering can be changed. For example, sometimes a
junction is external controlled but it could become a
free junction as the effect of the other causes.
STABLE STATES TRANSITION APPROACH - A New Strategy for Walking Robots Control in Uncertain Environments
203

The mathematical model of this object is a
Variable Causality Dynamic Systems (VCDS) and
will be analyzed from this point of view.
Irrespective of the leg numbers, any walking
robot, evolving in a vertical plane with a rigid body,
has only two legs as a support on the ground.
The ground, at the time moment t, is defined by
an unknown equation.
()
zx,t=ψ
(12)
about which only some values are obtained
()
z* x*, t *=ψ
(13)
as a result of feet testing at time instant t*.
A pair of legs
ij
{L , L }, i, j {1, 2, 3}, i j∈≠
constitutes the so called Active Pair of Legs (APL) if
the robot body position is the same irrespective of
the feet position of all the other legs different of L
i
(the prime-active leg) and L
j
(the second-active leg).
A robot is a fixed robot on the ground (FRG) if
its position is constant in time when both all its
commands and the ground are time invariant
()
(
)
x,t x , t
ψ
=
ψ
∀
(14)
A robot containing N proper legs can have only
N
a
numbers of APL,
2
aN
NC N(N1)/2== −
(15)
In this case N=3 so N
a
=3. All the other legs that
at a time instant do not belong to APL are called
Passive Legs (PL).
A label is assigned to each possible APL. The
APL label is expressed by a variable q called Index
of Activity (IA) that can take N
a
values, numbers or
strings of characters. For example the string of
characters, q='ijp', points out that the pair
ij
{L , L }
is
an APL and the leg L
p
is a passive leg. Instead of
strings of characters, the IA can take numerical
values as for example,
q123 i1;j2;p3,=⇔===⇔
i1j2p3
LL;LL;L L;== =
3 VARIABLE CAUSALITY
MATHEMATICAL MODEL OF
THE WALKING ROBOT
A good description for walking robot behavior is as
a VCDS. In such a system, all the variables that
characterize its behavior (the terminal variables) are
represented by a matrix X called the global variable
of the system. In the case of the above robot, the
matrix X is a 16x5 matrix. The first four columns of
this matrix contain variables related to the legs L
k
k=1:4 and the fifth variable related to the robot body
or other useful information.
For example, the k-column contains
X
k
=[u
1,k
, u
2,k
, R
k
, G
k
, s
k
, α
k
, β
k
, a
k
, b
k
, λ
k
],
k=1:4, where s
k
expresses the state of the k leg L
k
and the fifth column contains
X
5
=[O
0
, θ
, ε
12
, ε
23
, ε
31
,...]
where ε
12
, ε
23
, ε
31
express the stability indexes.
A distinction has to be pointed out between the
walking robot as a physical object, which has a
mathematical model, and different systemic input-
output representations generated by this
mathematical model.
These different systemic input-output
representations refer specially to different VCDS
extensions of the walking robot model subsystems.
VCDS representations are used in the SSTA control
algorithm of the walking robot.
According to SSTA, all the control actions are
closed loop performed. Both the sequence of
different types of movements and evolutions inside
of each specific movement, depend on the general
walking robot behavior objective and the
environment only.
Even if, as a physical object, the walking robot
has some command parameters, it behaves as a
VCDS because of the internal kinematics restrictions
that determine mechanical locks of the rigid body.
For example in this paper the variables
1,I 2, I
u,u ,I {1,2,3,4}=
(16)
are the command parameters, as inputs to robot
actuators, but discrepancies can appear between the
values as desired values supplied by the control
device and the realized values of these parameters.
In addition, a physical robot can have the possibility
of controlling its causal structure through a new
variable cz. For example, the angle
2, j
u is set as free
angle or other angles intentionally are set free. The
values of the free variables depend on the kinematics
restrictions or depend on the position parameters,
intentionally some how modified. For example, it is
possible externally to modify the position vector R
i
or only its real or imaginary part
kk,x k,y
RR jR,k1:4=+⋅ =. All these justify the
interpretation of the walking robot as VCDS.
In the framework of VCDS description, inputs
and outputs do not exist. All the variables are
terminal variables satisfying the System Existence
Relation (SER). As long as the system exists, the
SER is true according to a causality ordering
specified by the variable cz which acts as a true
input variable.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
204

In the VCDS approach with discrete time
evolution, the global variable X is represented by
three instants:
d
k
X ,
k1
X
−
and
k
X which respectively
express: the desired value at the current step, the
previous value and the actual realized value.
Depending on the actual value of the ordering
structure signal
k
cz , and the actual value of the
index of activity signal
k
q , only some components
of the matrix
d
k
X are effectively realized.
The VCDS evolution equation of the WR is
d
kk1kkk
X F(X ,X ,q ,cz )
−
=
(17)
The VCDS model of the walking robot is used in
the SSTA control structure proposed by the authors.
The behavior of the walking robot in different causal
structure is analyzed in details in other papers.
4 SSTA CONTROL STRUCTURE
It is consider that the walking robot has to evolve in
space along a direction Ox, which determines a
vertical section in the plane xOz of the evolution
environment as an unpredictable but measurable
function, called also the ground,
z(x)=
ψ
(18)
The evaluation of the curve
(x)
ψ
can be
performed by using walking robot external tools or
by using its legs for ground testing.
Evolution of the walking robot on unpredicted
ground
(x)
ψ
implies performing very complex
movements for walking robot legs. They must be
coordinated in such a way to avoid ground collision
during gaiting. Generally, in classical approaches,
the legs movements are predetermined, specifically
for different typical shapes of the ground.
The general block diagram of SSTA walking
robot control is presented in Fig.2.
Figure 2: The general block diagram of SSTA walking
robot control.
The evolution attitude refers, for example, to the
forward or backward evolution, having some
imposed fixed body angle, or variable body angle
but with maximum stability.
As a physical object, at a time moment t=kT, the
robot is controlled by the variables
kk k
u,q,cz
)
,
where
k
u
)
represents the matrix of the desired values
command angles of the proper legs
123
L,L ,L , and of
the head, assimilated as a leg,
4
L . So,
1,1 1,2 1,3 1,4
kkkk
k
2,1 2,2 2,3 2,4
kkkk
uuuu
u
uuuu
⎡
⎤
=
⎢
⎥
⎢
⎥
⎣
⎦
)
(19)
The variables
kk
q,cz, represent the values of the
activity index q and respectively the causal ordering
cz at the time moment t=kT. By
k
d there are
equivalently represented all the other disturbances
acting on the physical robot evolving in the
environment expressed by the function
Ψ . The
desired values
k
u
)
are applied to the positioning
systems, as a request, but they are not necessarily
realized. This depends on the values of
kk
q,cz.
Applying to the physical robot the desired
commands
k
u
)
, under the conditions of
kk k
q,cz, ,d
Ψ
, the global variable X, takes the value
k
X and the abscissa x of the robot centre point
0
O takes the value
k
x .
The values
kk
X,xwill be utilized by the control
algorithm in the next time step. The real evolution
ground, expressed by a function
Ψ is externally or
internally expressed by a function
*
Ψ , known, at
least, around the actual position of the robot.
5 IMPLEMENTATION OF THE
WALKING ROBOT CONTROL
ALGORITHM IN SSTA
STRATEGY
By SSTA strategy is assured the walking robots
evolution in uncertain environments subordinated to
two goals:
- achievement of the desired trajectory expressed by
the functions
0
z
Of(x)=
and (x)θ=θ , where x is
the ground abscissa and
0
x
Ox= ; it is considered the
evolution from left to right;
- assuarance of the system stability that is, in any
moment of the evolution the centre of gravity has to
be in the stability area.
Considering the walking robot as a variable
causality dynamic system it is possible to realize this
desideratum in different variants of assurance the
steps succession. The steps succesion suposes a
series of elementary actions that are accomplished
only if the stability condition exists.
STABLE STATES TRANSITION APPROACH - A New Strategy for Walking Robots Control in Uncertain Environments
205

Continuously, by sensorial means or using the
passive leg, the robot has informations about its
capacity of evolving on the ground. Every time it is
considered that the legs i, j are on the ground and the
the system is stable (
ij
[0,1]ε∈ ). The passive leg
p
G is which realises the walking.
By testing the ground is realized its division in
lots representing the fields on x axis which constitue
the abscissas of some points that can be touched by
the
p
G leg. The leg will always touch the ground
only on an admitted lot.
A next support point given by the free
p
G leg ,
is chosen so that to existe a next stable state
ip
ε
or
jp
ε
, taking into account the actual state of legs
activity. For example, if q=132, passive leg (which
tests) is
p
2
GG= and assures
12
[0,1]ε∈ or
23
[0,1]
ε
∈ . When the change of legs activity is
realised (q=123 or q=321 or q=231 etc.), the present
passive leg
p
G will become the leg i or the leg j.
In this paper, a variant of mouvements succesion,
composed by 12 steps, is proposed.
Figure 3: The graphical representation of SSTA walking strategy.
G
0
G
0
q=123
cz=[15 25 4]
12
[0,1]ε∈
q=123
cz=[15 25 0]
12
[0,1]ε∈
2
2
1
1
2
q=231
cz=[15 25 4]
23 13
[0,1]; [0,1]ε∈ ε∈
G
0
G
0
G
0
3
3
1
q=132
cz=[15 25 4]
13 12
[0,1]; [0,1]ε∈ ε∈
q=231
cz=[15 25 0]
23
[0,1]ε∈
q=132
cz=[15 25 0]
13
[0,1]ε∈
q=132
cz=[15 25 4]
13 23
[0,1]; [0,1]ε∈ ε∈
G
0
G
0
G
0
G
0
2
q=132
cz=[15 25 4]
13
[0,1]ε∈
q=231
cz=[15 25 4]
23
[0,1]ε∈
q=132
cz=[15 25 4]
13
[0,1]ε∈
q=132
cz=[15 25 0]
13
[0,1]ε∈
1
1
1
1
1
1
1
3
3
3
3
3
3
3
3
2
2
2
2
2
2
2
2
G
0
1
2
3
4
5
6
7
8
9
10
G
0
G
0
q=123
cz=[15 25 4]
12 13
[0,1]; [0,1]ε∈ ε∈
1
1
3
3
11
12
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
206
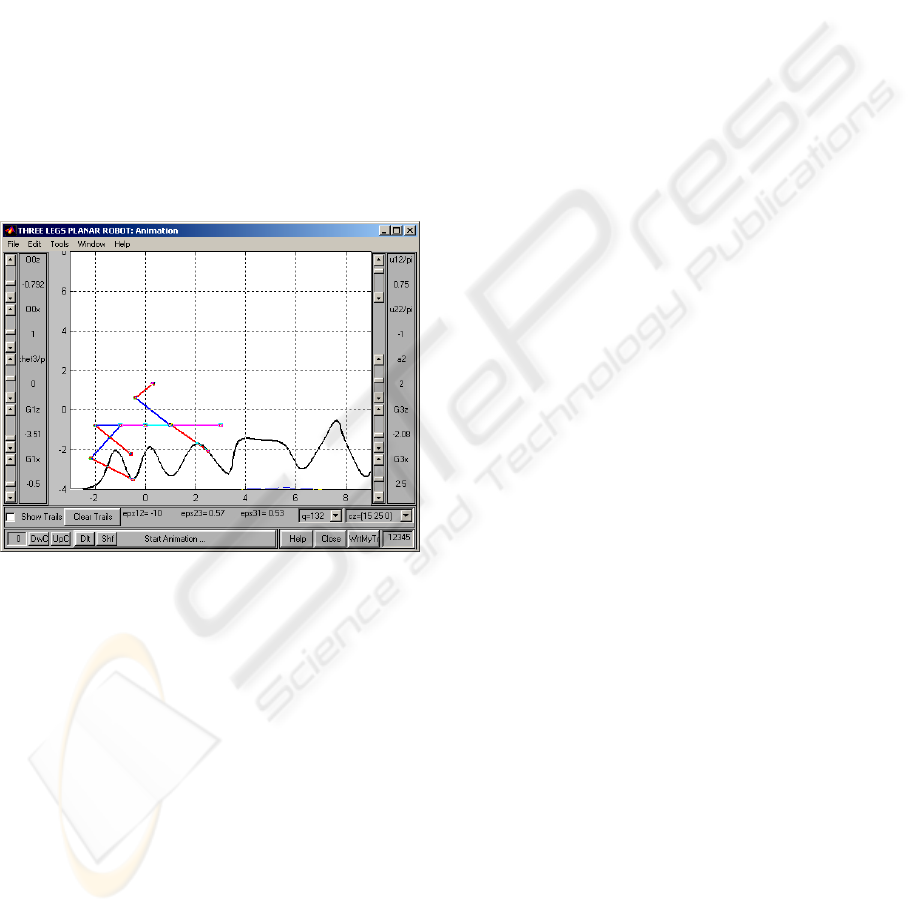
6 EXPERIMENTAL RESULTS
An experimental platform, called RoPa, has been
conceived. The RoPa platform is a complex of
MATLAB programs for simulation and control of
walking robots evolving in uncertain environments
according to SSTA control strategy.
A number of eight causality orderings of the
robotic structure have been implemented on RoPa.
Figure 4 presents the interface of this application
for the causality structure with four free joints. The
four degrees of freedom are thus consumed: one to
fulfil the kinematics restriction; one to ensure the
desired value of the θ angle of the robot body and
two for the desired values
000
xz
ˆ
O(O,O)
of the robot
body.
The causal ordering is activated by selecting the
causal variable cz=[15 25 0].
Figure 4: RoPa Graphic User Interface.
The stability of this evolution is graphical
represented by a stability certificate of the evolution.
This certificate attests the stability index of the
active pair of legs in any moment.
7 CONCLUSIONS
The experiments performed on RoPa demonstrate
the efficacy and adaptability of the proposed method
when the walking robots evolve in uncertain
environments. All the causal orderings are perfectly
integrated in RoPa structure proving the correctness
of the theoretical results.
The mathematical model developed in the paper
becomes an element of the VCDS walking robot
model. The robustness of this mathematical model
was proved by many experimental results
.
Further investigations will be directed towards a
hexapod robot performing a task in uncertain
environment.
REFERENCES
Cubero S., 2001. A 6-Legged Hybrid Walking and
Wheeled Vehicl
e. 7-th International Conference on
Mechatronics and Machine Vision in Practice, USA.
CWR, 2003. The Climbing and Walking Robots, Home
Page,
www.uwe.ac.uk/clawar.
Fulgenzi, C., Spalanzani A., Laugier C., 2007. Dynamic
Obstacle Avoidance in uncertain environment
combining PVOs and Occupancy Grid,
Robotics and
Automation
, 2007, pp.1610-1616.
Galt S., Luk L., 1999. Intelligent walking gait generation
for legged robots
. Proc. 2-th International Conference
on Climbing and Walking Robots
, pp.605-613.
Jung, S., Hsia, T.C., Bonitz, R., 2004. Force Tracking
Impedance Control of Robot Manipulators Under
Unknown Environment.
IEEE Transactions on
Control Systems Technology,
12(3), 474-483.
Kiguchi, K., Watanabe, K., Izumi, K., Fukuda, T., 2000.
Application of Multiple Fuzzy-Neuro Force
Controllers in an Unknown Environment Using
Genetic Algorithms,
Proc. of IEEE International
Conference on Robotics and Automation
, pp. 2106-
2111.
Kiguchi, K., Miyaji, H., Watanabe, K., Izumi, K., Fukuda,
T.,2000. Design of Neuro Force Controllers for
General Environments Using Genetic Programming,'
Proc. of the Fourth Asian Fuzzy Systems Symposium
(AFSS2000)
, pp. 668--673.
Nanayakkara, T., Watanabe K., Izumi, K., Kiguchi, K.,
2001. Evolutionary Learning of a Fuzzy Behavior
Based Controller for a Nonholonomic Mobile Robot in
a Class of Dynamic Environments,
Journal of
Intelligent and Robotic Systems
, Vol. 32, No. 3, pp.
255--277.
Nanayakkara, T., Watanabe, K., Kiguchi, K., Izumi, K.,
2001. Fuzzy Self-Adaptive Radial Basis Function
Neural Network-Based Control of a Seven-Link
Redundant Industrial Manipulator,
Advanced
Robotics,
Vol. 15, No. 1, pp. 17--43.
Sisil Kumarawadu, Keigo Watanabe, Kazuo Kiguchi, and
Kiyotaka Izumi, Neural Network-Based Optimal
Adaptive Tracking Using Genetic Algorithms,
Proc.of
4th Asian Control Conference,
pp105-110.
Schmuacer U., Schneider A. Ihme T., 1996. Six Legged
Robot for Service Operations.
Proc. of EOROBOT’96;
IEEE Computer Society Press
, pp:135-142.
Thirion, B., Thiry, L., 2001. Concurent Programming for
the Control of Hexapod Walking.
7-th International
Conference on Mechatronics and Machine Vision in
Practice,
USA.
STABLE STATES TRANSITION APPROACH - A New Strategy for Walking Robots Control in Uncertain Environments
207
