LEARNING DISCRETE PROBABILISTIC MODELS FOR
APPLICATION IN MULTIPLE FAULTS DETECTION
Luis E. Garza Casta˜n´on
Department of Mechatronics and Automation, ITESM Monterrey Campus, Mexico
Francisco J. Cant´u Ort´ız
Research and Graduate Programs Office, ITESM Monterrey Campus, Mexico
Rub´en Morales-Men´endez
Center of Innovation and Technology Design, ITESM Monterrey Campus, Mexico
Keywords:
Fault Detection, Bayesian Networks, Machine Learning, Power Networks.
Abstract:
We present a framework to detect faults in processes or systems based on probabilistic discrete models learned
from data. Our work is based on a residual generation scheme, where the prediction of a model for process
normal behavior is compared against measured process values. The residuals may indicate the presence of a
fault. The model consists of a general statistical inference engine operating on discrete spaces, and represents
the maximum entropy joint probability mass function (pmf) consistent with arbitrary lower order probabilities.
The joint pmf is a rich model that, once learned, allows us to address inference tasks, which can be used for
prediction applications. In our case the model allows the one step-ahead prediction of process variable, given
its past values. The relevant dependencies between the forecast variable and past values are learnt by applying
an algorithm to discover discrete bayesian network structures from data. The parameters of the statistical
engine are also learn by an approximate method proposed by Yan and Miller. We show the performance of the
prediction models and their application in power systems fault detection.
1 INTRODUCTION
The problem of fault detection in processes has re-
ceived great attention in last decades, and a wide vari-
ety of methods have been developed, most of them
based on fault detection and isolation (FDI) tech-
niques or in knowledge-based methods (Venkatasub-
ramanian et al., 2003). FDI is based on the use of an-
alytical redundancy rather than physical redundancy.
In FDI the redundancy in static and dynamic rela-
tionships between process inputs and outputs is ex-
ploited (Frank, 1990). The methods used by FDI can
be summarized in parity space approach, state estima-
tion approach, fault detection filtering, and parameter
identification approach. In every case, a mathemati-
cal model of process is required, either in state-space
or input-output form, but most of the time these mod-
els are linear systems. Since many processes exhibits
a nonlinear dynamics, several methods have been de-
veloped to deal with nonlinearities such as: decou-
pling approach, nonlinear observers and nolinear par-
ity spaces (Zhang and Ding, 2005). These methods
are limited to work well in a small region around the
point of operation or are adequate just for a limited
class of nonlinear systems.
In the other hand, Knowledege-based methods rely on
qualitative model descriptions in the form of neural
networks, Bayesian networks, fuzzy logic or qualita-
tive reasoning. Neural networks are widely used in
fault detection and diagnosis (Xu and Chow, 2005)
but they represent black box models and can not
deal with missing information. Fuzzy logic uses
a database with IF-THEN rules which use linguis-
tic variables. The problem with fuzzy logic is that
can not deal with incomplete information in explicit
form and the overall dimension of rules may blow up
strongly even for small processes (Isermann, 1997).
The methods based in qualitative reasoning require a
set of qualitative differential equations between pro-
cess variables not easy to obtain for complex pro-
cesses. Other machine learning approaches used
in fault detection can be found in (Sedighi et al.,
187
E. Garza Castañón L., J. Cantú Ortíz F. and Morales-Menéndez R. (2008).
LEARNING DISCRETE PROBABILISTIC MODELS FOR APPLICATION IN MULTIPLE FAULTS DETECTION.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 187-192
DOI: 10.5220/0001491801870192
Copyright
c
 SciTePress

2005; Davy et al., 2006). Bayesian networks (BNs)
have been lately used in fault detection and diagnosis
(Yongli et al., 2006; Matsuura and Yoneyama, 2004),
as they represent robust models for nonlinear systems
able to deal with missing information and noise. A
potential problem in BNs is the time for inference pro-
cess in large domains.
A recent trend is the combination of methods to take
advantage of the best aspects of every approach (Gen-
til et al., 2004). Our work is mainly focus in this di-
rection.
Our fault detection method is based on a predic-
tion model obtained from the process normal beha-
vior time series. We can find in technical literature
many approaches using machine learning techniques
for time series prediction. For instance, in (Luque
et al., 2007) an evolutionary approach is applied to
learn a set of rules to predict local behavior of time se-
ries. In (Chen and Zhang, 2005) an adaptive network
based fuzzy inference system (ANFIS) is used to pre-
dict chaotic and traffic flow time series. In (Vanajak-
shi and Rilett, 2007) a support vector machine (SVM)
approach is used to predict traffic flow time series. In
(Ma et al., 2007) evolving recurrent neural networks
are presented which predict chaotic time series. None
of these methods address the problem of missing in-
formation.
In our approach, we generate residuals by comparing
actual measurements against a prediction given by a
normal behavior model. The model structure and pa-
rameters are learned by applying machine learning
techniques. The residuals behavior indicate the ex-
istence of a fault.
We test our approach by diagnosing multiple-faults
events in a large power transmission network and
show promising results.
2 OUR APPROACH
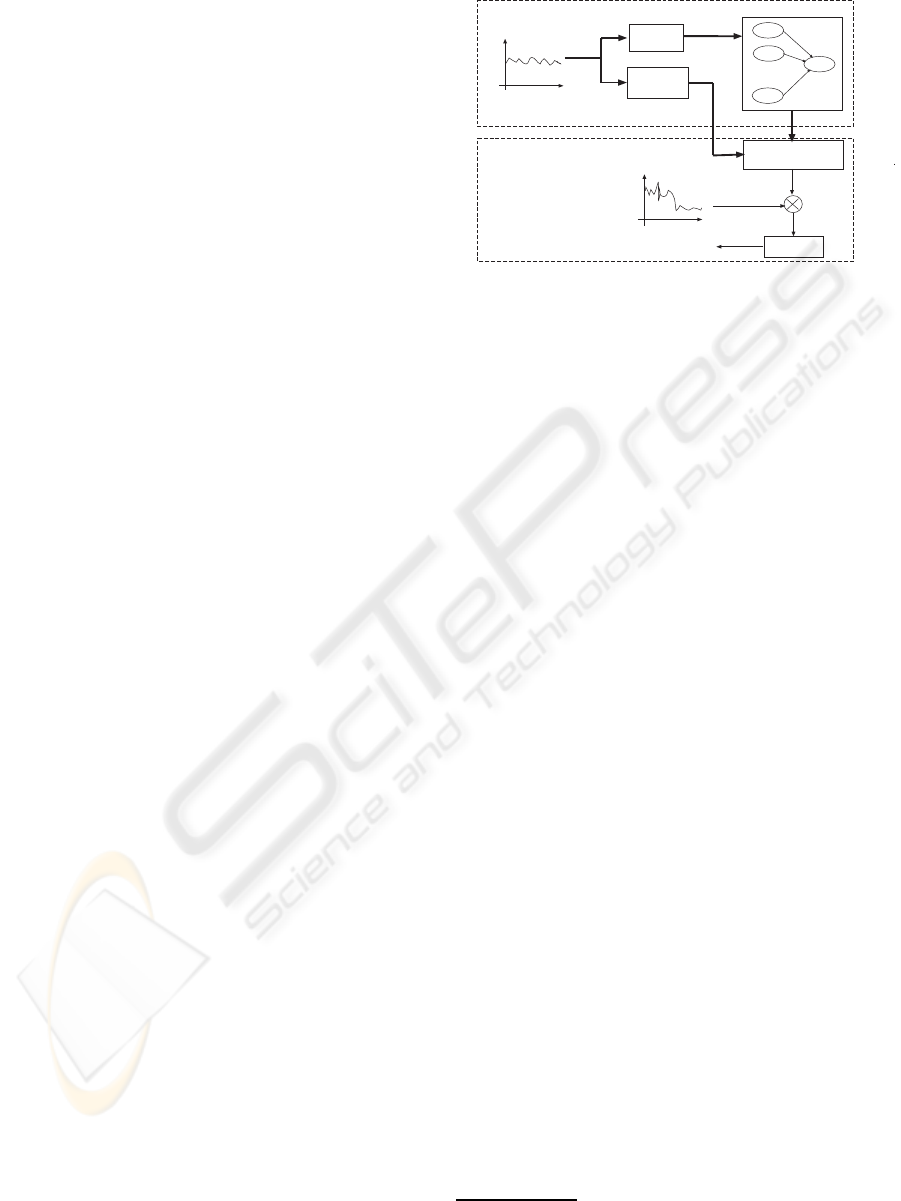
A general overview of the proposed approach is
shown in Figure 1. Basically we generate residuals
from the comparison between a process normal be-
havior model and the actual process values. We sub-
stitute the classical models of process normal behav-
ior (eg. discrete linear models) with a discrete prob-
abilistic function, whose parameters and structure are
learned off-line from normal behavior process data.
The probabilistic function is a general statistical in-
ference engine, which allows inference to know the
future value of a process variable, given its past val-
ues. In our case, we predict the one step-ahead value
of the process variable given a set of past values. The
set of relevant process variable values having direct
Steady State
Signal Behavior
Bayesian
Learning
Approach
Lagrange
Coefficients
Learning
Approach
X
t-1
X
t-2
X
t
X
t-n
.
.
Causal Model
Model Structure
Generation
OFFLINE PHASE
Prediction with
Statistical Maximum
Entropy Classifier
Residual
Analysis
Fault
Status
Data Window
to Analyze
ONLINE PHASE
Forecast
Xm
Real Data
Xk
Residuals
e=Xk-Xm
+
-
Figure 1: An overview of the fault detection approach based
on machine learning models.
influence on the forecast variable, are learned off-line
by using an algorithm to learn discrete Bayesian net-
works. The output of this algorithm is a graphical
causal structure, which is simplified by selecting the
Markov blanket of the forecast process variable. This
kind of compact probabilistic models are robust to
noise, incomplete information and nonlinearities.
In the decision and isolation step, we generate resid-
uals from the comparison between the output of the
probabilistic model and actual process variable val-
ues. The identification of the fault is performed by
a comparison of the residuals against a set of given
thresholds.
The architecture of the method is split in two phases:
the off-line phase and the online phase. The off-line
phase learns the model structure and parameters, and
the online phase take the decision regarding the pres-
ence of a fault.
2.1 The Off-line Phase
The off-line phase generates a discrete process nor-
mal behavior model from data, by applying machine
learning techniques which learn both: the model
structure and the parameters. The models can include
several variables having an influence over the state of
the process. The procedure to generate the models
starts with the discretization of continuous variables,
by using fixed bins or fuzzy clustering. The fixed in-
terval width discretization, merely divides the range
of observed values in equal sized bins. The general
idea with multivariate discretization approach based
on the fuzzy C-means algorithm (Wang, 1997), is that
rather than discretizing independently each variable,
we find the centroids of the c clusters defined by the
user, and assign each instance of the multivariate se-
ries to the closest cluster
1
.
1
According to a defined metric. We use a simple Eu-
clidean distance metric
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
188

1 4.766
2 4.764
3 4.839
4 5.003
5 5.018
6 5.057
7 5.154
8 5.362
9 5.425
10 5.570
9
9
9
10
10
10
11
12
12
13
Process Variable
values
Discretization
k=16
9 9 9 10 10
9 9 10 10 10
9 9 9 10 10
9 10 10 10 11
10 10 10 11 12
9 9 9 10 10
10 10 11 12 12
10 11 12 12 13
Construction of the set of
instances
Time Window
X
t-4
X
t-3
X
t-2
X
t-1
X
t
Figure 2: Selection of attributes with M
d
= 5.
The process of discretization allows the use of stan-
dard discrete Bayesian networks learning algorithms
and the implementation of the algorithm to learn the
general statistical inference engine parameters.
Once the discretization phase has been achieved, the
next issue in the construction of the model, is the
specification of the set of attributes and the instances,
to be supplied to the algorithm that learns the discrete
Bayesian network structure. This is not a trivial is-
sue, since possibly we do not know anything about the
lagged dependencies in the process variable dynam-
ics. If we have observed a sample of N data for the
variable X, the forecast or prediction variable X
t
may
depend on any of the past values X
t−1
,X
t−2
,... , X
t−N
.
We solve this problem by selecting an initial set of at-
tributes M
d
2
and keep adding attributes until a causal
structure can be found. Although it is possible that
different causal structures can be found, even a trivial
structure with just two nodes, we can test each struc-
ture and select the more accurate. If a causal structure
cannot be found with a discretization policy, then in-
crease the number of bins, in fixed discretization pol-
icy, or increase the number of clusters, in the fuzzy
C-means discretization policy, and again do the itera-
tive selection of the size of attributes. An example of
the selection of the attributes in a time series is shown
in figure 2, with M
d
= 5. The input to the discrete
bayesian networks learning algorithm is thus a set of
instances having the form {X
t−M
d
−1
,... , X
t
}. Notice
we are not assuming beforehand anything regarding
independence of variables or specific time dependen-
cies. The algorithm that learns the Bayesian network
structure tries to find such dependencies.
When the causal structure of the set of M
d
at-
tributes is found, we select our model from the
Markov blanket of the prediction variable X
t
. The
2
M
d
is also the size of the time window, and the in-
stances are formed sliding the time window through the
complete time series. In a time series with N data we can
have N − M
d
+ 1 instances
Figure 3: (a) Chua’s electric circuit, (b) Learned graphical
models from data.
Markov blanket in a BN consists of node’s parents, its
children and its children’s parents. The Markov blan-
ket forms a natural feature selection, as all features
outside the Markov blanket can be safely deleted from
the BN. We exploit this feature to produce a much
smaller causal structure for our forecast model, with-
out compromising the classification accuracy.
The prediction variable is the M
d
th attribute, has P
parents (variables influencing directly its value) and
no children (other variables over which the forecast
variable have an influence). We enforce this by spec-
ifying a variable ordering to the BN learning algo-
rithm. For instance, Figure 3 shows the models ob-
tained for an electrical circuit which behaves as a
chaotic system. X
1
represents electrical current across
the inductance L and X
2
and X
3
represent voltages at
capacitors C
1
and C
2
.
After we obtain the relevant past values for the
forecast variable, we learn the parameters of the sta-
tistical inference engine based on the maximum en-
tropy principle. This method can be stated as follows:
Consider a random feature vector
ˆ
F = (F,C), F =
(F
1
,F
2
,... , F
N
), with F
i
∈ A
i
and A
i
the finite set
{1,2, 3,...,|A
i
|}, and C ∈ {1,2, .. . ,K}. Denote the
full discrete feature space by G ≡ A
1
× A
2
··· × A
N
×
C . Suppose we are given knowledge of all (N(N −
1)/2) pairwise pmf’s {P[F
m
,C],∀m} and wish to con-
strain the joint pmf P[F, C] to agree with these. The
pairwise probabilities typically are estimated from
training set co-occurrence counts. The maximum en-
tropy (ME) joint pmf consistent with these pairwise
pmf’s has the Gibbs form:
P[C = c|F = f] =
exp

N
∑
i=1
γ(F
i
= f
i
,C = c)

K
∑
c
′
=1
exp

N
∑
i=1
γ(F
i
= f
i
,C = c
′
)

(1)
LEARNING DISCRETE PROBABILISTIC MODELS FOR APPLICATION IN MULTIPLE FAULTS DETECTION
189

0 50 100 150 200 250 300 350 400 450 500
-8
-6
-4
-2
0
2
4
6
8
Time
X1 (volts) X2(volts) X3(amperes)
Chua’s Circuit Modeling with C-means clustering (16 states)
X2
X3
X1
Figure 4: Modeling Chua’s circut parameters with a C-
Means clustering discretization method.
where
• F is the set of relevant past values for the forecast
variable,
• C is the set of predicted variables.
The subset of model parameters (Lagrange
multipliers) {γ(C
i
= c
i
,F = f),i = 1, . . . ,N,c
i
=
1,... ,K, f = 1,... ,K} are learned with a determin-
istic annealing algorithm. Where N is the number of
relevant past values for the prediction variable, K is
the number of discretization bins.
We need to supply following inputs to the Lagrange
coefficients learning algorithm:
• A training set of P +1 attributes with M instances,
• a training set support size G
s
<< G ,
• an annealing parameter η,
• an annealing threshold ε,
• an annealing initial temperature T
max
and final
temperature T
min
• a ρ learning-rate parameter.
The inference engine provides a probability distribu-
tion of the forecast variable, given the evidence of
relevant past values of forecast variable. We select
the discrete state with highest probability and to make
a comparison against the real data, we substitute the
state by its correspondent real value. An example of
modeling is shown in Figure 4.
2.2 The Online Phase
In order to perform process fault detection, the obser-
vations or measurements obtained from the process,
have to be compared against the prediction given by
the normal behavior model. From this comparison,
the residuals are generated and then analyzed to give
a decision about the behavior of the component.
If we denote X
t
as the measurement of a component
variable at time t, and
ˆ
X
t
as the prediction of the com-
ponent variable given by the steady state model, then
the residual e
t
is computed from:
e
t
= X
t
−
ˆ
X
t
(2)
The differences between the steady-state model
and the real data, e
t
, are transformed to a filtered ver-
sion of residuals, using the equation:
¯e
t
= ¯e
t−1
+ λ∗ (|e
t
| − ¯e
t−1
)
The value of λ, between 0 and 1, represents the
smoothing factor of the residuals. We refer to the av-
erage value of a set of filtered residuals as the error
weighted moving average (EWMA) index. An exam-
ple of EWMA residuals behavior in Chua’s electri-
cal circuit is shown in figure 5 under normal circum-
stances, and in figure 6 under an additive fault.
The fault decision is accomplished by comparing
the actual filtered residuals against the limit thresh-
olds of each fault mode. The limit thresholds are cal-
culated previously from process data. In our case, we
perform intensive simulations in a power transmis-
sion network which include single faults and different
combinations of multiple faults.
1500 1600 1700 1800 1900 2000 2100 2200 2300 2400 2500
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Time
EWMA Value
Chua’s Circuit EWMA Indexes Behavior for Normal State
X2
X3
X1
Figure 5: EWMA residuals behavior in normal operation of
the three parameters in Chua’s circuit.
1500 1600 1700 1800 1900 2000 2100 2200 2300 2400 2500
0
0.5
1
1.5
2
2.5
3
3.5
Time
EWMA Value
Chua’s Circuit EWMA Indexes Behavior for Abrupt Fault at X1
X1
X3
X2
Figure 6: EWMA residuals behavior in an additive fault at
X
1
in Chua’s circuit.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
190

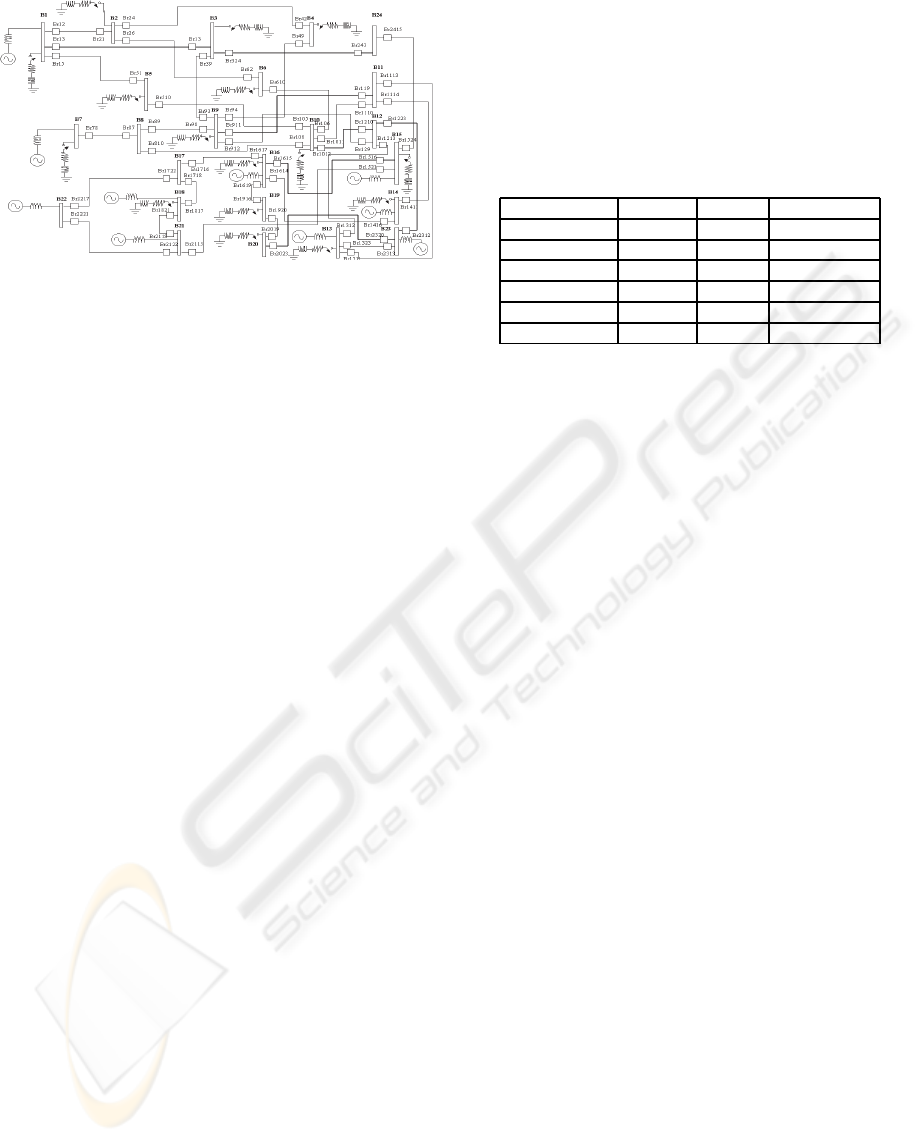
Figure 7: The electrical power network test system.
3 CASE STUDY
We illustrate the application of our approach in a sim-
ulated power transmission network, shown in fig. 7.
The system consists of 24 nodes, 34 lines and 68
breakers. The electrical power network is supplied
with the energy produced by three-phase generators.
Ideally, the generators supply the energy to three-
phase balanced loads, which means that every load
has an identical impedance. In a balanced circuit,
each phase has the same magnitude of voltage, but
displaced 120 electrical degrees. In all simulations
we include dynamic behavior by varying resistive-
inductive loads in several nodes.
A fault in a electric network is any event that in-
terfere with the normal flow of current. The faults
in an electrical power network can be divided in two
types: symmetrical faults and unsymmetrical faults.
The symmetrical faults involve the three phases of the
system, are relatively easy to evaluate, and represent
about the 5 % of the fault cases. The unsymmetrical
faults involve some kind of unbalance, and include
line to ground faults and line to line faults. The line
to ground faults represent about 70 % of the faults,
and the line to line faults represent about 25 % of the
cases (Grainger and Stevenson, 1994).
The diagnosis in large power networks is a difficult
task, mainly due to overwhelming amount of data, the
cascaded effect, and the uncertainty in the informa-
tion. The main protection breakers of a node can be
opened (as a secondary protection) by faults at neigh-
bor nodes, giving rise to ambiguous diagnoses. The
voltage measurements at a given node, are also per-
turbed by faults at neighbor nodes.
With our modeling approach, we represent the steady
state dynamics of continuous signals (e.g. voltages) in
every node, and detect different types of faults: sym-
metrical faults (e.g. a three-phase to ground fault) and
unsymmetrical faults (e.g. a line-to-ground fault).
To evaluate the degree of success in the identification
of the faulty components, we ran a set of 48 simula-
tions in the power network. We randomly simulate si-
multaneous different types of faults in several nodes.
The type of faults included symmetrical and unsym-
metrical faults.
Table 1: Performance evaluation by type of fault.
Fault Type Correct Wrong % Accuracy
A-B-C-GND 18 0 100.0
A-B-GND 12 0 100.0
A-GND 16 3 84.2
A-B 18 4 81.8
B-C 22 0 100.0
NO FAULT 20 7 74.0
The results obtained (see table 1) show that we
were able to determine with great accuracy the sym-
metrical faults, but we have problems with false pos-
itive detections and line-to-line faults.
We also performed an evaluation with a level of 30 %
of random missing information in the same test nodes
data. The steady state models were learned with a
training set of data with just 10% of random missing
information. The computed EWMA indices remain
almost in the same values (±2%) computed without
missing information. The evaluation with missing in-
formation, delivered the same fault identification as
the evaluation without missing information.
4 DISCUSSION
This approach is intended to work with data coming
from multiple sources. The intention is to build, with
this data, models which are robust to incomplete in-
formation and non-linearities. We have tested in some
examples the capabilities of model to approximate
nonlinear dynamics. The accuracy of the model, is
related mainly to the level of discretization and the
learning time of model’s parameters. If we increase
the level of discretization, we also need to increase the
set support G
s
of model’s parameters learning algo-
rithm, with the consequence of rising significatively
the learning time. For instance, with 16 states and a
set support size of 50 elements, learning time was 7.5
hours (using a desktop computer with a 1.3 GHz pro-
cessor clock). If we increase the number of states to
32, the learning time was 12.5 hours. If we just in-
crease the set support size for 16 states, from 50 to 80
elements, the learning time increases to 15 hours.
In summary, we do not think we have a restriction on
the kind of applications we can tackle due to the accu-
racy of the model. All we need is a level of accuracy
LEARNING DISCRETE PROBABILISTIC MODELS FOR APPLICATION IN MULTIPLE FAULTS DETECTION
191

enough to distinguish between normal operation and
every type of fault. We think that a level of discretiza-
tion of at most 32 states, will cover many of the fault
detection applications.
5 CONCLUSIONS AND FUTURE
WORK
We have presented a new approach to detect faults
based on models learned by machine learning tech-
niques. The model represents the process normal be-
havior and is used in a residual generation scheme
where model output is compared against actual pro-
cess values. The residuals generated from this com-
parison are used to indicate the existence of a fault.
The compact learned models are robust to noise, miss-
ing information and nonlinearities. We apply our
method in a very difficult domain, as it is an electri-
cal power network. The noise in data, the cascaded
effect, and the perturbation by neighbor nodes, makes
the diagnosis task hard to achieve. We have shown
good levels of accuracy in the determination of the
real faulted components and the mode of fault, in
multiple events, multiple mode fault scenarios, where
missing information was given. We determine in ex-
perimental simulations that wrong node state identifi-
cations were mainly due to the overlapping between
EWMA indices thresholds, giving rise to ambiguous
fault decisions. We plan to reach higher levels of suc-
cess with the help of more reliable signal change de-
tection methods.
REFERENCES
Chen, D. and Zhang, J. (2005). Time series prediction based
on ensemble anfis. In Proceedings of the fourth Inter-
national Conference on Machine Learning and Cyber-
netics. IEEE.
Davy, M., Desorbry, F., Gretton, A., and Doncarli, C.
(2006). An online support vector machine for abnor-
mal events detection. In Signal Processing 86 (2006).
Elsevier.
Frank, P. (1990). Fault diagnosis in dynamic systems unisg
analytical and knowledge based redundancy a survey
and new results. In Automatica. Elsevier.
Gentil, S., Montmain, J., and Combastel, C. (2004). Com-
bining fdi and ai approaches within causal-model-
based diagnosis. In IEEE Transactions on Systems,
Man and Cybernetics, part B. IEEE.
Grainger, W. and Stevenson, W. (1994). Power Systems
Analysis. McGraw-Hill, USA.
Isermann, R. (1997). On fuzzy logic applications for au-
tomatic control, supervision, and fault diagnosis. In
IEEE Transactions on Systems, Man, and Cybernet-
ics. IEEE.
Luque, C., Valss, J., and Isasi, P. (2007). Time series fore-
casting by means of evolutionary algorithms. In Pro-
ceedings of the Parallel and Distributed Processing
Symposium 2007. IEEE.
Ma, Q., Zheng, Q., Peng, H., Zhong, T., and Xu, L. (2007).
Chaotic time series prediction based on evolving re-
current neural networks. In Proceedings of the fourth
International Conference on Machine Learning and
Cybernetics. IEEE.
Matsuura, J. P. and Yoneyama, T. (2004). Learning bayesian
networks for fault detection. In International Work-
shop on Machine Learning for Signal Processing.
IEEE.
Sedighi, A., Haghifam, M., and Malik, O. (2005). Soft com-
puting applications in high impedance fault detection
in distribution systems. In Electric Power Systems Re-
search 76 (2005). Elsevier.
Vanajakshi, L. and Rilett, L. (2007). Support vector ma-
chine technique for the short term prediction of travel
time. In Proceedings of the 2007 Intelligent Vehicles
Symposium. IEEE.
Venkatasubramanian, V., Rengaswamy, R., k. Yin, and
Kavuri, S. (2003). A review of process fault detection
and diagnosis part 1, part 2 and part 3. In Computers
and Chemical Engineering. Elsevier.
Wang, L. (1997). A Course in Fuzzy Systems and Control.
Prentice Hall, USA.
Xu, L. and Chow, M. (2005). Power distribution systems
fault case identification using logistic regression and
artificial neural network. In Proceedings of the 13th
International Conference on Intelligent Systems Ap-
plication to Power Systems.
Yongli, Z., Limin, H., and Jinling, L. (2006). Bayesian
networks-based approach for power systems fault di-
agnosis. In IEEE Transactions on Power Delivery.
IEEE.
Zhang, P. and Ding, S. X. (2005). A simple fault detec-
tion scheme for nonlinear systems. In Proceedings of
the 2005 IEEE International Symposium on Intelligent
Control. IEEE.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
192