AUTOMATED SIZING OF ANALOG CIRCUITS BASED ON

GENETIC ALGORITHM WITH PARAMETER

ORTHOGONALIZATION PROCEDURE

Masanori Natsui and Yoshiaki Tadokorot

Dept. of Information and Computer Sciences, Toyohashi University of Technology

1-1 Hibarigaoka, Tempaku-cho, Toyohashi-shi, Aichi 441-8580, Japan

Keywords: Evolutionary computation, Circuit synthesis, Analog circuits, Genetic algorithms, Principal component anal-

ysis.

Abstract: This paper presents a method for the automated sizing of analog circuits using genetic algorithm (GA). For the

rapid and efﬁcient exploration of GA, we introduce the idea of search space sphering and dimension reduction

with principal component analysis (PCA). The potential capability of the system is demonstrated through

the automated sizing of wide-swing current mirror circuit. Experimental results show that the system with

PCA successfuly generates higher-performance circuits under given evaluation function on average, and the

dimensionally reduction method further improves the performance of solutions.

1 INTRODUCTION

Electronic design automation (EDA) has matured as

a technology to be universally accepted for produc-

ing highly integrated VLSI systems. However, there

still remain many difﬁcult design problems to be ad-

dressed in the advanced SoC (System on Chip) era.

In this paper, we propose an automated analog

circuit design method based on evolutionary compu-

tation. An analog circuit inherently involves trade-

offs among a large number of performance metrics

and the performance is determined by the complex

and nonlinear nature of relations between the topol-

ogy and parameter values (e.g. device sizes) of a cir-

cuit. Therefore, the analog circuit design often re-

quires simultaneous optimization of circuit topology

and parameter values. It requires the knowledge and

experience of experts who had trained in a particular

way to understand circuit/device technologies. This

is the major motivation to introduce evolutionary op-

timization techniques for the design automation.

There are already some approaches to the evolu-

tionary design of analog circuit structures(Koza et al.,

1997; Lohn and Colombano, 1999; Shibata and Fu-

jii, 2001). The reference (Koza et al., 1997) de-

scribes various analog circuit design including ana-

log ﬁlters and ampliﬁers by means of genetic pro-

gramming (GP). The reference (Lohn and Colom-

bano, 1999) proposes a method of representing elec-

tronic circuit structures by “linear representation” and

its application to analog circuit synthesis using ge-

netic algorithm (GA). The reference (Shibata and Fu-

jii, 2001) also applies GA to the synthesis of analog

circuits based on current path based coding. These

approaches appear to perform both topology and pa-

rameter optimization equally. Both approaches have

the possibilities of ﬁnding best possible solutions un-

der given conditions and constraints since both topol-

ogy and parameter optimization are performed simul-

taneously. However, the simultaneous optimization

often leads to an explosion of search space, which re-

quires much computation time for ﬁnding a solution,

and sometimes converges into a local optimum.

To make our method suitable for practical use, we

have proposed a two-stage optimization process of

analog circuits as follows: (i) topology-oriented opti-

mization using evolutionary computation and (ii) de-

tailed optimization of parameter values (e.g. aspect

ratios of transistors) using a commercially available

automatic circuit sizing software(Homma et al., 2000;

Homma et al., 2002; Natsui et al., 2005; Natsui et al.,

2007). This storategy have achieveda reduction in the

size of search space and an improvement in the search

efﬁciency.

In this paper, we mainly focus on an automated

analog circuit sizing for a given circuit topology by

193

Natsui M. and Tadokorot Y. (2008).

AUTOMATED SIZING OF ANALOG CIRCUITS BASED ON GENETIC ALGORITHM WITH PARAMETER ORTHOGONALIZATION PROCEDURE.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 193-199

DOI: 10.5220/0001492301930199

 SciTePress

using GA. In order to accelerate the search efﬁciency

of the circuit sizing system, we propose the idea of

applying the parameter orthogonalization procedure

based on principal component analysis (PCA) to the

system. In the analog circuit design, the relative scale

between circuit parameters such as the ratio of the

length and width of a transistor or that of the widths

of two transistors has an important role to determine

circuit performance. If the system can consider the

correlations between parameters that are speciﬁc to

higher-ﬁtness individuals and periodically reduce the

search space, it can increase the search efﬁciency of

the optimization process.

From this viewpoint, we introduce a search space

reduction operation based on PCA. The principal

component-based exploration realizes efﬁcient pa-

rameter optimization, and additionally, dimensional-

ity reduction method further reduces the search space.

As a result, we can realize the high-performance op-

timization system which ﬁnds the optimal parameter

set with less computation time.

The potential capability of the proposed system

is demonstrated through the automated circuit sizing

of a wide-swing current mirror, which is one of the

most popular building block in analog circuit design.

This paper is organized as follows: Section 2 presents

the basic concept of the GA-based automated circuit

sizing system and its extension using PCA. Section 3

demonstrates the experimental result. Section 4 is the

conclusion and future prospects.

2 GA-BASED AUTOMATED

CIRCUIT SIZING SYSTEM AND

ITS EXTENSION USING PCA

2.1 Genetic Algorithm

Genetic algorithm (GA) can be regarded as a unique

variation of evolutionary computation techniques

(Back et al., 1997; Holland, 1975; Goldberg, 1989).

In general, evolutionary methods mimic the process

of natural evolution, the driving process for emer-

gence of complex structures well-adapted to the given

environment. The better an individual performs under

the conditions the greater is the chance for the individ-

ual to live for a longer while and generate offspring.

As a result, the individuals are transformed to the suit-

able forms on the designer’s deﬁned constraint.

Figure 1 shows the overall procedure of GA. At

ﬁrst, GA generates embryonic individuals randomly

to form the initial population P(0). Note that usually

each individual is represented by a ﬁxed-length bit

program Genetic Algorithm;

begin

t := 0;

{t: Number of generations.}

initialize(P(t));

{P(t): Population.}

evaluate(P(t));

while t ≤ Max. num. o f gen. do

begin

C(t) := crossover(P(t));

M(t) := mutation(P(t));

evaluate(C(t) ∪ M(t));

P(t + 1) := select(C(t) ∪ M(t) ∪ P(t));

t := t +1;

end

end.

Figure 1: Typical ﬂow of GA.

string in the traditional GA, while our system applies

real-coded genetic algorithm (RCGA) (Eshelman and

Schaffer, 1993) which uses a real number vector rep-

resentation of chromosomes.

The next step is to evaluate a ﬁtness function of

all individuals in P(t). A value for ﬁtness is assigned

to each individual depending on how close it actu-

ally is to solving the problem. Since typical analog

circuits have various performance metrics, an ana-

log circuit optimization problem is usually formu-

lated as (1) a single-objective optimization problem

where different performance objectives are combined

to form a scalar objective, or (2) a multiobjectiveopti-

mization problem based on Pareto-optimality(Somani

et al., 2007). In our system, we apply the single-

objective approach for the system simplicity and rea-

sonable computational effort. Thus a synthetic ﬁtness

function for a circuit is deﬁned by the combination of

ﬁtness functions for various performance objectives.

After the evaluation, the system selects a set of in-

dividuals having higher ﬁtness values to perform evo-

lutionary operations: crossover and mutation. The

crossover recombines two individuals into two new

offsprings. The mutation operation, on the other

hand, changes the values of chosen genes randomly.

There are many ways how to do crossover and muta-

tion. In our system, we apply blend crossover (BLX-

α)(Fig. 2) and uniform mutation. Blend crossover

generates the offspring vectors X

= (x

,··· ,x

)

and X

= (x

,··· ,x

) from parant vectors P

, p

,··· , p

) and P

= (p

, p

,··· , p

) by

= γp

+ (1 − γ)p

and x

= (1 − γ)p

+ γp

where γ = (1+2α)u

−α, u

∈ [0,1] is a random value.

Uniform mutation, on the other hand, changes the

value of the element to a value chosen from the uni-

form distribution on the speciﬁed interval.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

194

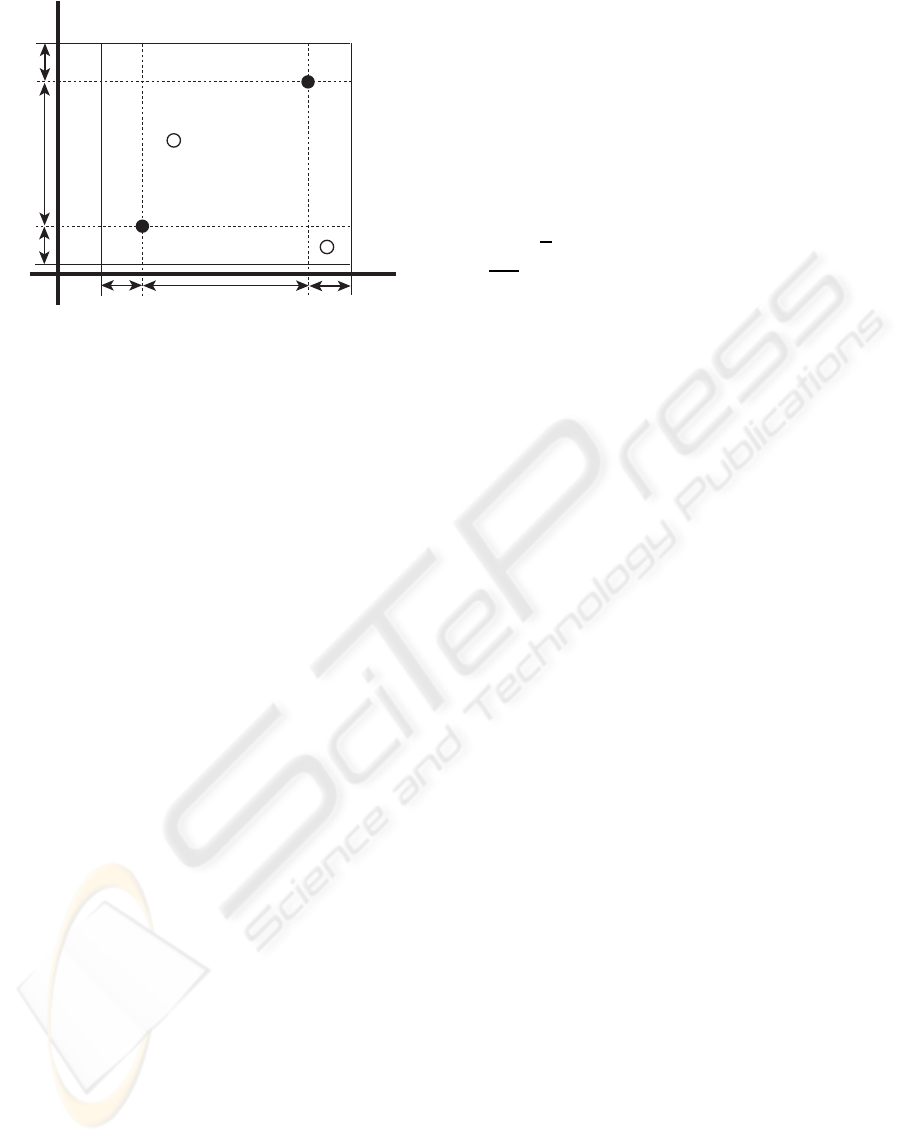
Parameter 1

Parameter 2

Parent 1

Parent 2

Child 1

Child 2

Figure 2: Blend crossover for two parameter vectors.

2.2 Search Space Reduction using PCA

Let us consider the search space reduction method of

the automated analog circuit sizing on the basis of

common characteristics of higher-ﬁtness individuals.

Given individuals which have averagely higher ﬁt-

ness values after a certain generations, one of the sim-

plest way is to narrow down the search space of each

parameter independently according to its mean and

variance. If the parameters are orthogonalized and

noncorrelated, this approach may work well. How-

ever in the case of analog circuit sizing, it sometimes

fails and the exploration process converges to a local

minimum since these parameters usually have strong

correlations mutually. In order to perform effective

search space reduction, we should apply an appropri-

ate reduction method considering its relationship.

From this viewpoint, we utilize a coordinate trans-

form procedure based on principal component analy-

sis (PCA) to ﬁnd a rotated orthogonal system such

that the elements in the new coordinates are uncorre-

lated. PCA is a well known method for reducing the

dimensionality by extracting components which are

uncorrelated with each other, and has been used in a

wide range of research including signal processing,

statistics, and neural computing, as the powerful tool

of data analysis and compression (Jolliffe, 2002). The

exploration and search space correction based on the

principal components and their variances have a pos-

sibility of enhancing the efﬁciency of the parameter

optimization of GA.

The parameter orthogonalization procedure by

PCA can be performed by the following steps:

1. Selects a set of higher-ﬁtness individuals, where

the parameter set corresponding to the ith individ-

ual is represented by x

= (x

,··· ,x

2. Generates a parameter matrix

X =



















... x







where each row corresponds a parameter set of an

individual.

3. Generates a matrix

X = ( ˜x

) by normalizing

values of the matrix X so as to the mean

∑

i=1

˜x

= 0 and the variance σ

N−1

∑

i=1

( ˜x

− µ

)

= 1 for each column.

4. Calculates a variance-covariance matrix, eigen-

values and eigenvectors of

5. Calculates an orthogonalized parameter matrix

′

XA = (x

′

) where A is a matrix such that

each column contains coefﬁcients for one princi-

pal component.

6. Applies x

′

= (x

′

,··· ,x

′

) to the parameter set

corresponding to the ith individual.

The orthogonalization procedure is performed peri-

odically with a speciﬁc interval during the evolution

process by GA. This means that the system always

use the vectors of real number elements with µ = 0

and σ

= 1 for the individual representation, while the

search space of circuit parameters is periodically cor-

rected depending on the distribution of higher-ﬁtness

individuals. Additionally, if the variation of the last

principal components are sufﬁciently small, we can

eliminate these components from an exploration and

reduce the length of individuals since they contribute

relatively little extra information of individuals. This

dimensionality reduction further improves the search

efﬁciency, and reduces the total computational time.

When the system evaluates the evolved individ-

uals, corresponding circuit parameters are restored

by performing the above operation in reverse order

(Fig. 3). Moreover, the restored parameters are quan-

tized with a certain step depending on a variance of

each parameter and the minimum step size of a tar-

get fabrication process. In our system, the param-

eters are quantized with step size σ

/10, where σ

is a variance of the jth parameter. If σ

/10 is less

than the minimum step size, the system applies the

latter value. It realizes a coarse-to-ﬁne search strat-

egy, which achieves an effective exploration due to

the prevention of the search space explosion of GA.

3 EXPERIMENT

We implement a GA-based automated analog circuit

sizing system. The system applies GA to search the

AUTOMATED SIZING OF ANALOG CIRCUITS BASED ON GENETIC ALGORITHM WITH PARAMETER

ORTHOGONALIZATION PROCEDURE

195

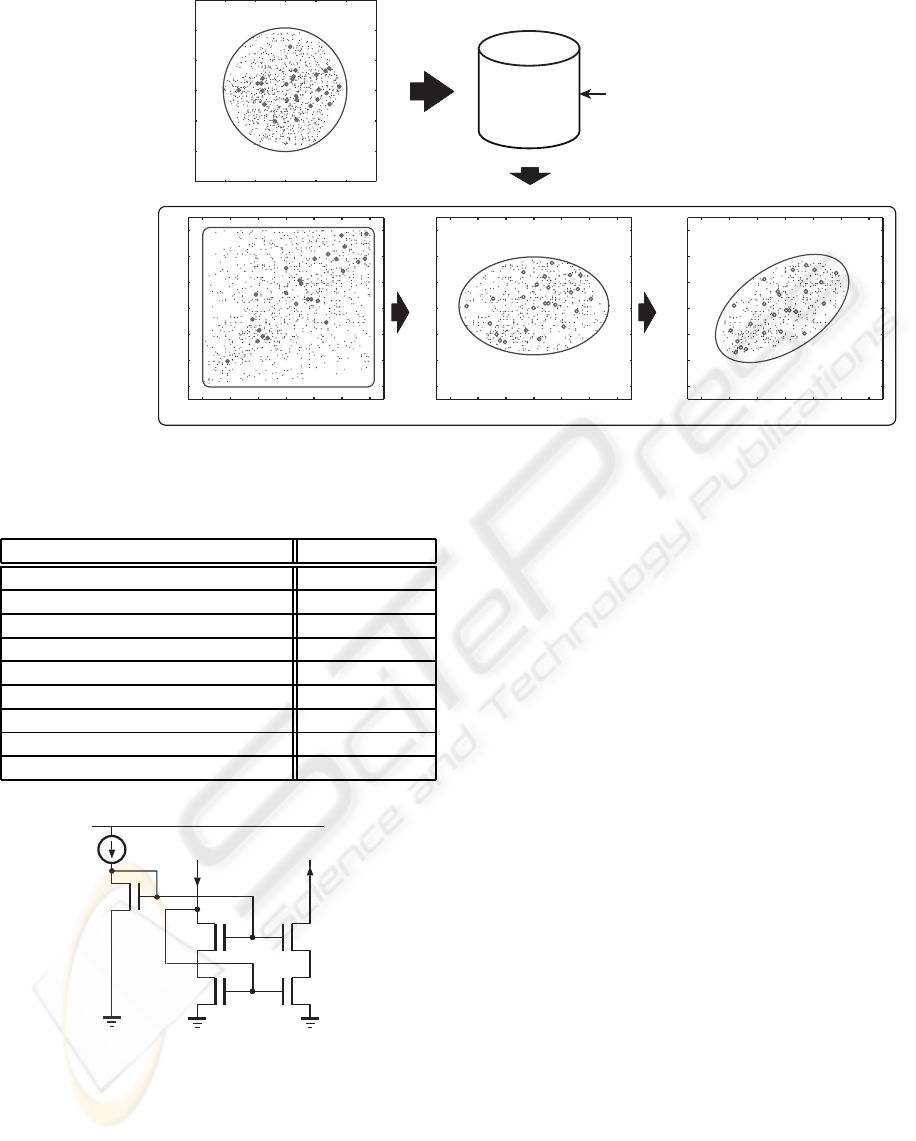
Matrix A’

Mean

Variance

Parameter 1

Parameter 2

Principal component 1

Principal component 2

Parameter 1

Parameter 2

Parameter 1

Parameter 2

Periodically updated

Parameter restration

Genotype

(Principal components)

Phenotype

(Circuit parameters)

Figure 3: Parameter restoration (A

′

is a matrix such that AA

′

= I).

Table 1: Main parameter values for GA.

Parameter Value

Maximum number of generations 500

Population size 200

Crossover method BLX-0.5

Crossover rate 0.7

Mutation rate 0.1

Mutation method Uniform

Selection method Rank & Elitist

Interval of PCA execution 20

Num. of individuals for PCA 20

VDD

Iref

Tr5

Tr1

out

Iin

Tr2

Tr3 Tr4

Figure 4: Wide-swing nMOS current mirror.

optimal set of circuit parameters (transistor length L

and width W) which achieves higher performance on

a given circuit topology, and periodically the orthog-

onalization procedure using PCA is performed to cor-

rect the search space of the optimization. After up-

dating a characteristic vector matrix, the system de-

stroys the lower-ﬁtness individuals and creates ran-

domly generated ones to form a population of the next

generation.

The design speciﬁcation considered here is a

wide-swing nMOS current mirror (Fig. 4), which is

widely used in analog integrated circuits both as a

biasing element and as a load device for ampliﬁer

stage(Gray et al., 2001). The basic function of cur-

rent mirrors is to produce an output current i

equal

to the input current i

multiplied by a desired current

gain B, that is, i

= −B× i

. Ideally the gain B is in-

dependent of the input frequency, the output current

is independent of the output voltage v

, the input

voltage drop v

equals zero, and the circuit area is as

small as possible. In practice, the characteristics of

real current mirrors deviate from those of ideal ones.

There are various possible choices for a current mirror

structure due to the trade-offs among the characteris-

tics.

Design parameters of this circuit structure are

,···,W

,···,L

), where W

and L

are the

width and length of the MOS transistor Tr

, respec-

tively. The generated individual is translated into the

corresponding netlist, which is simulated to analyze

its electrical behavior and characteristics with SPICE

simulations. Traditionally a weighted sum of the ﬁt-

ness functions has been used for the function aggre-

gation. However, for nonlinear optimization prob-

lems like analog circuit sizing where the different ob-

jectives have nonlinear dependence upon each other,

this approach sometimes causes some difﬁculties and

leads to the premature convergence of the evolution

process. For example, if one objective is easier to at-

tain a target performance than other objectives, the

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

196

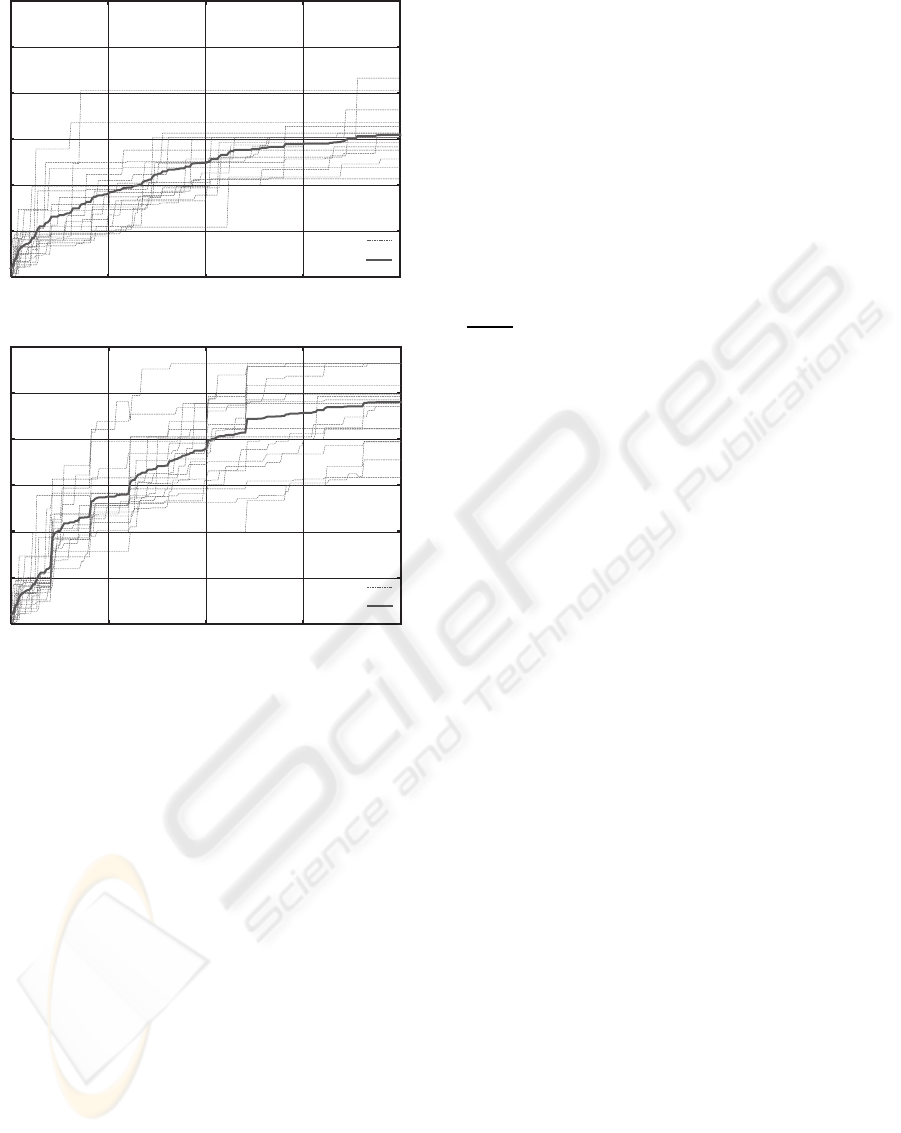
(a)

(b)

Best individual fitness (20 runs)

Average for 20 runs

0 50 100 150 200

Generations

Normalized synthetic fitness

Best individual fitness (20 runs)

Average for 20 runs

0 50 100 150 200

Generations

Figure 5: Fitness transition: (a) the conventional system, (b)

the proposed system with PCA (The synthetic ﬁtness values

are normalized into 0 ≤ F ≤ 1).

population sometimes convergesto the speciﬁc search

space, which leads to the evolutionary stasis. For sat-

isfying all the objectivesat the end of the optimization

run, all the different ﬁtness functions must be normal-

ized and weighted equally.

In order to prevent the system from the premature

convergnce, we deﬁne the synthetic evaluation func-

tion F as follows:

F =

∏

i=1

where F

evaluates the accuracy in i

-i

characteristic,

evaluates the output saturation voltage investigated

through DC transfer analysis, and F

evaluates the in-

put impedance. The value of F

is determined accord-

ing to the rank of the ith characteristic in a population

and is normalized into 0 ≤ F

≤ 1. Thus the optimiza-

tion process advances towards searching a parameter

set which realizes higher performance synthetically.

Note that only when the ith characteristic of an indi-

vidual cannot be simulated by SPICE, F

is set to 0

and the synthetic ﬁtness value of the individual is also

set to 0, which will be eliminated in the selection op-

eration.

For more effecient exploration, we need further

investigation of ﬁnding more proper ﬁtness function.

The result would be reported in the future.

In order to demonstrate the speciﬁc advantage of

the search space reduction using PCA, we carry out

experiments on generating an optimal parameter set

of the given current mirror circuit structure. Table

1 summarizes the system parameters in this experi-

ment. We set 0.6µm ≤ W

≤ 60µm and 0.6µm ≤ W

≤

60µm, and the minimum step size of these parame-

ters is 0.1µm. Thus the size of the possible choices is

(

60−0.6

0.1

)

≃ 5.47 × 10

, which needs 93 bits for an

individual representation in traditional GA. By apply-

ing parameter quantizetion method described above,

on the other hand, the proposed system limits the size

to 10

at most, which needs 34 bits, and the possible

choices of circuit parameters are changed depending

on the result of PCA.

Figure 5 shows the effect of PCA-based search

space reduction by comparing the average ﬁtness

transitions. The system with PCA shows the tendency

to improve the ﬁtness more rapidly. It clearly shows

that the proposed system explores a search space and

ﬁnds better implementations more effectively com-

pared with the conventional system.

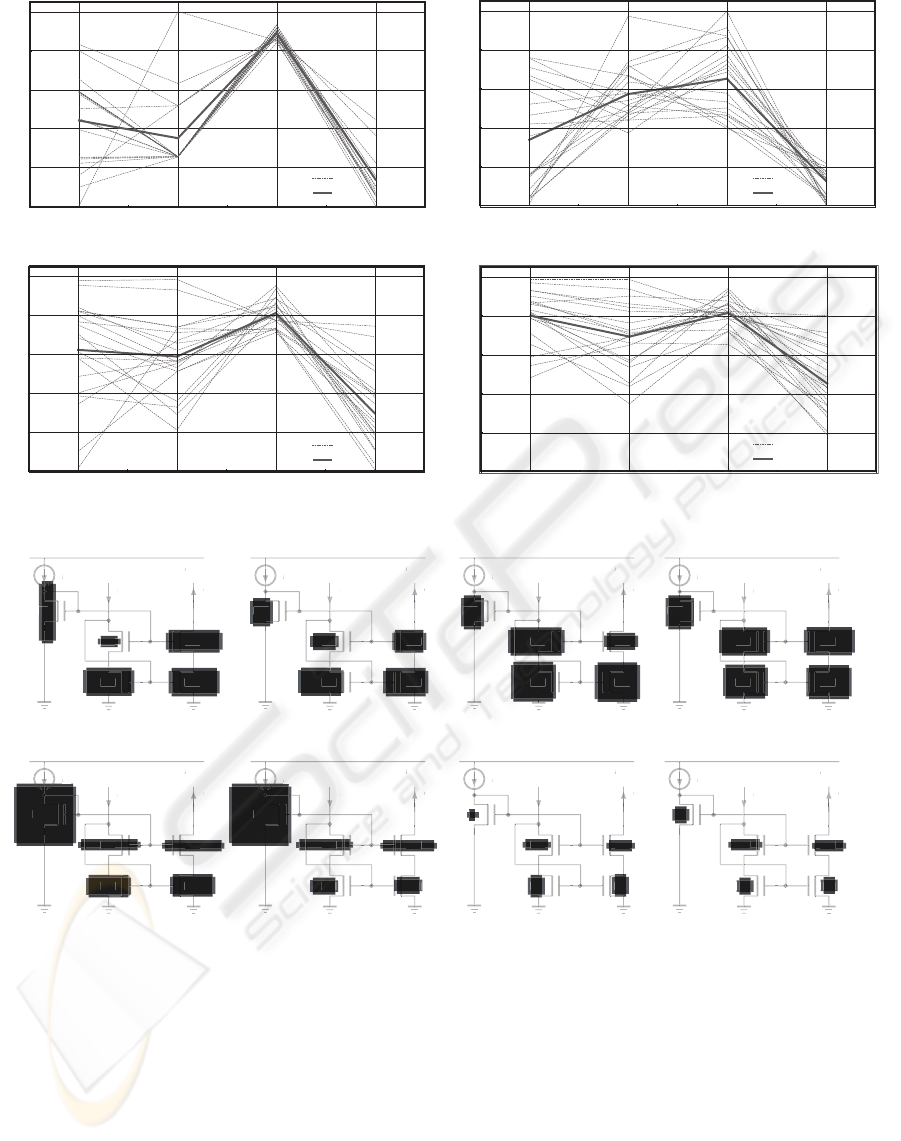
Next, we evaluate the effect of applying PCA on

the performance of evolved solutions. Figure 6 com-

pares the performance of evolved circuits on

(a) the conventional system,

(b) the system with the search space reduction ac-

cording to their means and variances indepen-

dently,

procedure by PCA,

(d) the system with the parameter orthogonaliza-

tion procedure and dimensionally reduction using

PCA.

We performed 20 distinct evolutionary runs for each

condition. We can see that the system with PCA gen-

erated higher-performance circuits under given eval-

uation function on average, and the dimensionally re-

duction method further improved the performance of

evolved solutions.

In the following, we analyze one successful evo-

lutionary process in detail. Figure 7 depicts an ex-

ample snapshot of the evolved best ﬁtness individ-

ual on each generation. The transistor sizes of them

are described graphically. Given the initial random

population, the system searches the set of parameters

having higher ﬁtness value for a while. At the 31st

AUTOMATED SIZING OF ANALOG CIRCUITS BASED ON GENETIC ALGORITHM WITH PARAMETER

ORTHOGONALIZATION PROCEDURE

197

0.2

0.4

0.6

0.8

0.2

0.4

0.6

0.8

0.2

0.4

0.6

0.8

0.2

0.4

0.6

0.8

(a) (b)

Best individual fitness (20 runs)

Average for 20 runs

Best individual fitness (20 runs)

Average for 20 runs

Best individual fitness (20 runs)

Average for 20 runs

Best individual fitness (20 runs)

Average for 20 runs

Normalized fitness

Figure 6: Performance of evolved circuits.

ref

Tr5

Tr1

out

ref

out

ref

out

ref

out

ref

out

ref

out

ref

Tr5

out

Tr3

Tr4

ref

Tr5

out

Tr3

Tr4

0th generation 31st generation

108th generation

11th generation

Tr1

Tr2

Tr3

Tr4

Tr5

21st generation

51st generation 81st generation 101st generation

Tr1

Tr2

Tr3

Tr4

Tr5

ref

Tr5

ref

Tr5

Figure 7: Best ﬁtness individual transition.

generation, the system ﬁnds a set of parameters such

that (W1,L1,W3,L3) = (W2, L2,W4,L4), which is

known as the proper setting of this structure. After

that, the evolution process further improves the per-

formance by changing a set of parameters. We can see

that the best ﬁtness individuals after the 31st genera-

tion have a tendency of keeping the above ratio since

the parameter orthogonalization procedure is period-

ically performed to correct the search space. And ﬁ-

nally, the system reaches the optimal solution at the

108th generation. This result shows that the PCA-

based search space correction method works well and

the system can ﬁnd the optimal solutions effectively.

4 CONCLUSIONS

In this paper, we have presented a possibility of the

GA-based analog circuit sizing system and its perfor-

mance improvement using PCA-based orthogonaliza-

tion procedure. An experimental synthesis of a wide-

swing current mirror circuit demonstrates the poten-

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

198

tial capability of the proposed system to optimize

analog-digital-mixed architectures without using ex-

pert knowledge of transistor-level circuits.

The experimental result also suggests a possibil-

ity of constructing intelligent circuit synthesis sys-

tems, which may evolve its ability by accumulat-

ing design experience. By introducing the guidelines

for reusing suitable individuals, the proposed system

could achieve more signiﬁcant results.

ACKNOWLEDGEMENTS

This work was supported by Grant-in-Aid for Young

Scientists (B) (No. 18700044) from The Ministry of

Education,Culture,Sports,Science and Technology.

REFERENCES

Back, T., Hammel, U., and Schwefel, P. H. (1997). Evo-

lutionary computation: Comments on the history and

current state. IEEE Trans. Evolutionary Computation,

1(1):3 – 13.

Eshelman, L. J. and Schaffer, J. D. (1993). Real-coded ge-

netic algorithms and interval schemata. Foundations

of genetic algorithms 2, pages 187 – 202.

Goldberg, D. (1989). Genetic Algorithms in Search, Op-

timization and Machine Learning. Addison-Wasley

Publishing Company.

Gray, P. R., Hurst, P. J., Lewis, S. H., and Meyer, R. G.

(2001). Analysis and Design of Analog Integrated

Circuits (Fourth Edition). John Wiley & Sons.

Holland, J. H. (1975). Adaptation in Natural and Artiﬁcial

Systems. University of Michigan Press.

Homma, N., Aoki, T., and Higuchi, T. (2000). Evolution-

ary synthesis of fast constant-coefﬁcient multipliers.

IEICE Trans. Fundamentals, E83-A(9):1767–1777.

Homma, N., Aoki, T., and Higuchi, T. (2002). Evolutionary

graph generation system with transmigration capabil-

ity and its application to arithmetic circuit synthesis.

IEE Proc. Circuits Devices Syst., 149(2):97 – 104.

Jolliffe, I. T. (2002). Principal Component Analysis.

Springer.

Koza, R. J., III, Bennett, H. F., Andre, D., Keane, A. M.,

and Dunlap, F. (1997). Automated synthesis of analog

electrical circuits by means of genetic programming.

IEEE Trans. Evolutionary Computation, 1(2):109 –

128.

Lohn, D. J. and Colombano, S. P. (1999). A circuit represen-

tation technique for automated circuit design. IEEE

Trans. Evolutionary Computation, 3(3):205 – 219.

Natsui, M., Homma, N., Aoki, T., and Higuchi, T. (2005).

Design of multiple-valued logic circuits using graph-

based evolutionary synthesis. Journal of Multiple-

Valued Logic and Soft Computing, 11(5-6):519 – 544.

Natsui, M., Tadokoro, Y., Homma, N., Aoki, T., and

Higuchi, T. (2007). Synthesis of current mirrors based

on evolutionary graph generation with transmigration

capability. IEICE Electronics Express, 4(3):88 – 93.

Shibata, H. and Fujii, N. (2001). An evolutionary syn-

thesis of analog active circuits using current path

based coding. IEICE Trans. on Fundamentals, E84-

A(10):2561–2568.

Somani, A., Chakrabarti, P., and Patra, A. (2007). An evo-

lutionary algorithm-based approach to automated de-

sign of analog and rf circuits using adaptive normal-

ized cost functions. IEEE Trans. Evolutionary Com-

putation, 11(3):336 – 353.

AUTOMATED SIZING OF ANALOG CIRCUITS BASED ON GENETIC ALGORITHM WITH PARAMETER

ORTHOGONALIZATION PROCEDURE

199