ADAPTIVE RESOURCES CONSUMPTION IN A DYNAMIC AND

UNCERTAIN ENVIRONMENT

An Autonomous Rover Control Technique using Progressive Processing

Simon Le Gloannec, Abdel Illah Mouaddib

GREYC UMR 6072, Universit´e de Caen Basse-Normandie, Campus Cˆote de Nacre

bd Mar´echal Juin, BP5186, 14032 Caen Cedex, France

Franc¸ois Charpillet

MAIA team, LORIA, Campus Scientiﬁque, BP 239, 54506 Vandœuvre-l`es-Nancy Cedex, France

Keywords:

MDP, Resource-bounded Reasoning, Hierarchical control, Autonomous agents, Planning and Scheduling.

Abstract:

This paper address the problem of an autonomous rover that have limited consumable resources to accomplish

a mission. The robot has to cope with limited resources: it must decide the resource among to spent at each

mission step. The resource consumption is also uncertain. Progressive processing is a meta level reasoning

model particulary adapted for this kind of mission. Previous works have shown how to obtain an optimal

resource consumption policy using a Markov decision process (MDP). Here, we make the assumption that

the mission can dynamically change during execution time. Therefore, the agent must adapt to the current

situation, in order to save resources for the most interesting future tasks. Because of the dynamic environment,

the agent cannot calculate a new optimal policy online. However, it is possible to compute an approximate

value function. We will show that the robot will behave as good as if it knew the optimal policy.

1 INTRODUCTION

Resources consumption control is crucial in the au-

tonomous rover context. For example, a rover must

know when it has to go back to a docking station be-

fore having no energy left. The question for the agent

is to know where, when, and the amount of resources

it has to spend for a particular task. We want this

agent to be adaptive : it has to choose the amount

of resources to spend in each task by taking into ac-

count the expected value. This is the reason why we

use progressive processing to modeland to control the

mission. This model of reasoning describes tasks that

can be performed progressively, with several options

at each step. The resources consumption is proba-

bilistic. Progressive processing provides a meta-level

resources consumption model. Then, we obtain an

optimal policy control thanks to a MDP.

For now, progressive processing does not cope

with dynamic environments. In a real robot applica-

tion, it is not uncommon to see new tasks incoming

during the mission. When it happens, the agent has

to completely recalculate the resource control policy

to behave optimally. Most of the time, it doesn’t have

sufﬁcient time to do it. For these reasons, we propose

here a value function approximation method that al-

lows the agent to compute a local near optimal pol-

icy very quickly in order to cope with the dynamic

changes. We will bring experimental result to vali-

date this method.

The paper is divided into ﬁve main sections. The

third section introduces progressive processing and its

use for an autonomous rover mission application. In

the fourth section, we present the dynamic environ-

ment and propose a way to cope with changes during

the mission. This theory is experimentally validated

in the last section.

2 RELATED WORK

• Control of Progressive Processing: Progressive

processing has been introduced in (Mouaddib and

Zilberstein, 1998), and has been used in a real

rover application (Zilberstein et al., 2002) and in

a retrieval information engine (Arnt et al., 2004).

Concerningthe retrievalinformation engine, users

send requests to a server that can respond very

200

Le Gloannec S., Illah Mouaddib A. and Charpillet F. (2008).

ADAPTIVE RESOURCES CONSUMPTION IN A DYNAMIC AND UNCERTAIN ENVIRONMENT - An Autonomous Rover Control Technique using

Progressive Processing.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 200-206

DOI: 10.5220/0001492802000206

 SciTePress

precisely and use lots of resources, or approxima-

tively and use less resources. Progressive process-

ing permits to model the server tasks. It also per-

mits to adapt the resources dedicated to each task

by taking the number of requests into account. We

will brieﬂy presentthe rover application in this pa-

per.

• MDP Decomposition: an MDP is used to for-

malise the mission resource consumption control.

We can either compute an optimal policy or an

approximate policy. Our approximation is based

on MDP decomposition. This technique has been

largely studied in the literature. Dean et al (Dean

and Lin, 1995) investigated methods that decom-

pose global planning problems into a number of

local problem. In (Parr, 1998), the method is to

build a cache of policies for each part of the prob-

lem independently, and then to combinethe pieces

in separate steps. (Meuleau et al., 1998) also

proposed a decomposition technique for a prob-

lem where tasks have indepedent utilities, and are

weakly coupled.

• Value Function Approximation: our work also

deals with value functionapproximation. In (Feng

et al., 2004), the state space is dynamically par-

titioned into regions where the value function is

the same throughout the region. Authors make

piecewise constant and piecewise linear approx-

imations. (Pineau et al., 2003) introduced point

base value iteration. It approximates an exact

value iteration solution by selecting a small set

of representative belief points and by tracking the

value and its derivative for those points only.

3 MODEL A MISSION WITH

PROGRESSIVE PROCESSING

The problem formalism will be presented hierarchi-

cally: the mission is divided into progressive process-

ing units (PRU), which are separated into levels.

3.1 Formalism

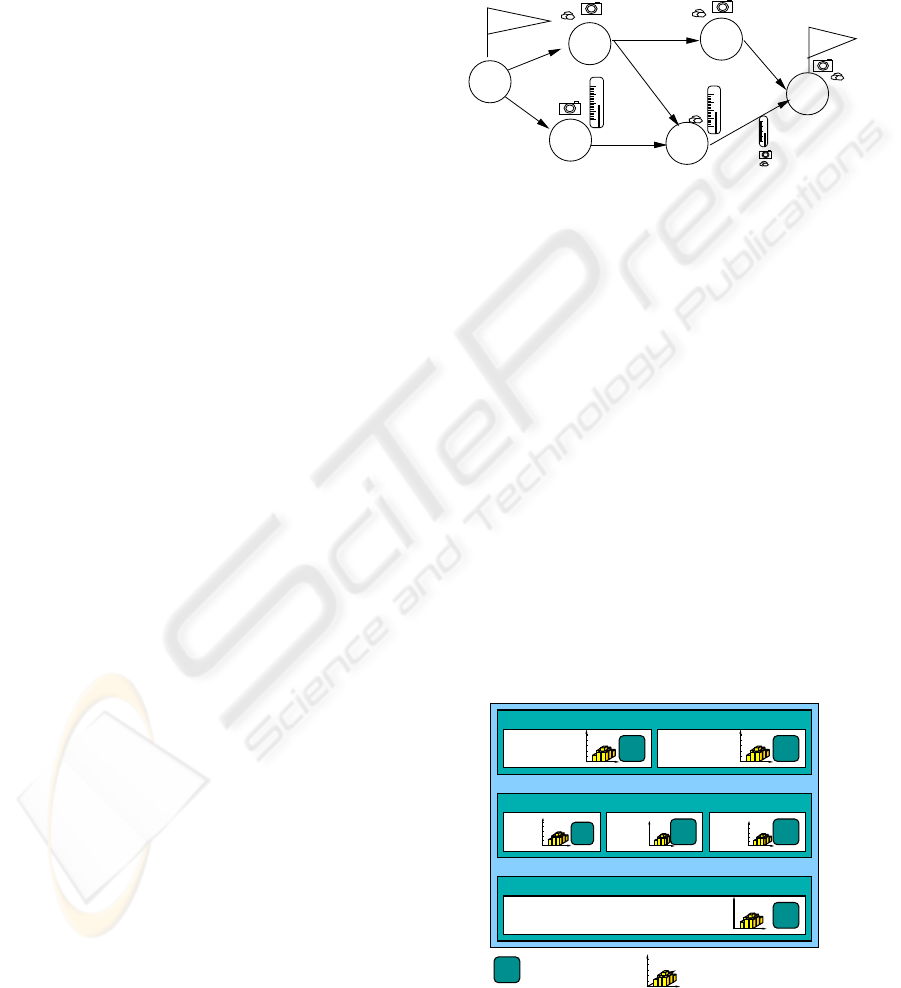
A mission is a set of tasks, and each task is an acyclic

graph vertex (see Figure 1). To facilitate access to

the formalism, we assume that this acyclic graph is an

ordered sequence. This involves no loss of generality.

You can see this sequence as a particular path in the

graph (for example A, B, E, F). There are P tasks in

the sequence. Each task is modelled by a progressive

processing unit (PRU). It is structured hierarchically.

Each PRU

, p ∈ {1,... ,P} is a level ordered ﬁnite

sequence [L

p,1

,.. . ,L

p,L

]. An agent can process a level

only if the precedinglevel is ﬁnished. The process can

be interrupted after each level. It means that the agent

can stop the PRU execution, but it receives no reward

for it. Other situations have been proposed when the

agent can have a reward at each level. However, in our

case, only a complete task accomplishment provides

a reward.

Site

End

Site

Picture analysis

Weather analysis

Rock analysis

Start

Site

Figure 1: A mission.

Each level L

p,ℓ

contains one or more modules

p,ℓ,1

,.. . ,m

p,ℓ,M

]. A module is a speciﬁc way to ex-

ecute a level. The agent can only execute one module

per level. The execution of a module produces a qual-

ity Q and consumes resources. A progressive pro-

cessing unit deﬁnition is illustrated on Figure 2 for a

picture task. Firstly, the rover has to aim its camera,

then it chooses the picture resolution. At the end, it

saves the picture. The execution is performed from

bottom to top.

The quality Q

p,ℓ,m

∈ R

is a criterion to measure

the module execution impact. There is no immediate

reward after each level processing. The agent receives

the sum of all the Q

p,ℓ,m

only when the last level is

performed.

The resource consumption in a module m

p,ℓ,m

probabilistic. We denote as P r

p,ℓ,m

the probability dis-

tribution of resources consumption.

PRU

Level 1

Level 2

Level 3

4 53

0.1

0.2

4 53

0.1

0.2

4 53

0.1

0.2

4 53

0.1

0.2

4 53

0.1

0.2

4 53

0.1

0.2

4 53

0.1

0.2

ressources consumption

probability distribution

Q Q

module quality

res

med

res

high

high comp low comp

aim camera

low

res

Figure 2: PRU.

ADAPTIVE RESOURCES CONSUMPTION IN A DYNAMIC AND UNCERTAIN ENVIRONMENT - An Autonomous

Rover Control Technique using Progressive Processing

201

3.2 Mission Control

The problem of control we address in this paper con-

sists of a robot exploring an area where it has sites

to visit and performs exploration tasks. The problem

is that the robot cannot know in advance its resource

consumption. We use then a MDP to control the mis-

sion. The agent is supposed to be rational. It must

maximise the mathematical expected value. It com-

putes a policy that correspond to this criterion before

executing the mission. The on-line mission control

process consists in following this policy. In the next

section, we present the MDP model and the control

policy calculation. At each site the agent must take a

decision to stay for continuing the exploration or to

move to another site.

3.2.1 Modelling the Mission as an Markov

Decision Process

Formally, a MDP is tuple {S ,A ,P r,R } where :

• S is a ﬁnite set of states,

• A is a ﬁnite set of actions,

• P r is a mapping S × A × S → [0,1],

• R : S → R is a reward function.

Given a particular rational criterion, algorithms

for solving MDPs can return a policy π, that maps

from S to A , and a real-valued function V : S → R.

Here, the criterion is to maximise the expected reward

sum.

3.2.2 States

In the progressive processing model, a state is a tu-

ple hr,Q,p,ℓi. r is a reel number that indicates the

amount of remaining resources. Q is the cumulated

quality since the beginning of the current PRU. p and

ℓ indicates the last executed level L

p,ℓ

done. The fail-

ure state, denoted as s

failure

is reached when the re-

source quantity is negative. The reward is assigned

to the agent only when the last level of the PRU has

been successfully executed. Then, it is necessary to

store the cumulated quality Q in the state description.

We have introduced level 0 in order to represent the

situation where the agent begins the PRU execution.

3.2.3 Actions

There are two kinds of actions in the progressive

processing model. An agent can execute only one

module in the next level or move to the next PRU.

These two actions are depicted in Figure 3. Formally,

A = {E

,M}. When the agent reaches the last level

in a PRU

, it directly moves to the next PRU

p+1

2, 1

2, 2

2, 3

3, 2

3, 1

1, 1

next PRU

Level 1

Level 2

Level 3

Level 1

Level 3

Level 2

current PRU

1, 1

Figure 3: Actions.

Actually, E

is an improvement of the the current

PRU whereas M is an interruption. The agent can pro-

gressively improvethe PRU execution, it can also stop

it at any moment.

3.2.4 Transitions

M is a deterministic action whereas E

is not. Indeed,

the module execution consumes resources and this

consumption is probabilistic. After executing a given

module, the agent always cumulates a ﬁxed quality.

The uncertainty is related to the resources consump-

tion probability distribution. Thus,

P r(hr,Q, p,ℓi,M,hr,0, p + 1,0i) = 1

P r(hr,p, Q,ℓi,E

,hr

′

,p,ℓ + 1i)= P r(∆r|m

p,ℓ,m

)

where Q

′

= Q+ Q

p,ℓ,m

and r

′

= r − ∆r

(1)

3.2.5 Reward

A reward is given to the agent as soon as it ﬁnishes a

PRU. This reward corresponds to the cumulated qual-

ity through the modules path. If the agent leaves a

PRU without ﬁnishing it, it receives no reward. This

makes a sense for explorationtask where the robothas

no reward if the task is not completely ﬁnished.

R (hr,Q,p,L

i) = Q (2)

R (hr,Q,p,ℓ < L

i) = 0 (3)

where L

is the number of levels in PRU

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

202

3.2.6 Value Function

The controlpolicy π : S → A dependson a value func-

tion that is calculated thanks to the Bellman equa-

tion 4. We assume that V (s

failure

) = 0.

V (hr,Q,p,ℓi) =



0 if r < 0 (failure)

R (hr,Q,p, ℓi) + max(V

) otherwise

(hr,Q, p,ℓi) =



0 if p = P

V (hr,0,p + 1,0i) otherwise

(hr,Q, p,ℓi) =











0 if ℓ = L

max

∑

∆r

P r(∆r|m

p,ℓ,m

).V (hr

′

,p,ℓ + 1i)

where Q

′

= Q+ Q

p,ℓ,m

and r

′

= r − ∆r

(4)

Action E consumes some resources whereas M

does not. The agentwill execute the module that gives

it the best expected value.

3.3 Control Policy

The main objective is to compute a policy that the

robot will follow in order to optimise the resource

consumption during the mission. It has been proven

that we could calculate an optimal policy (Mouaddib

and Zilberstein, 1998). When the mission is ﬁxed

before execution time, we can get this policy with a

backward chaining algorithm. With this policy, the

robot can choose at any moment the decision that

maximise the global utility function for the mission

i.e. the obtained reward sum. But, this policy is ﬁxed

for a given mission. If the mission changes during

execution time, this policy is no longer up to date.

Even if the policy algorithm is linear in the state

space, the time needed to compute the optimal policy

is often more than a module execution time. This oc-

curs especially when the mission (and then the state

space) is large. This is the reason why we propose an

other way to calculate the policy. We will not cal-

culate an optimal policy, but a near-optimal policy

which could be used to take good decision when the

mission changes.

4 THE DYNAMIC

ENVIRONMENT

We suppose in this paper that tasks can come or dis-

appear during execution time. This assumption is re-

alistic for an explorer rover.

Instead of seeing the control as a global policy for

the mission, we decompose it in two parts, the current

PRU and the rest of the mission. The policy is only

calculated for the current PRU. It only dependson the

expected value function for the rest of the mission.

We could yet obtain the optimal policy with this

method by simply calculating the expected value

function for the rest of the mission without any ap-

proximation. Thus, we will naturally not save time.

Then, we present here a method to calculate the ex-

pected value function very quickly.

5 VALUE FUNCTION

APPROXIMATION

The quick value function approximation is based on a

decomposition technique. Decomposition techniques

are often use in large Markov decision processes.

Here, we will re-compose an approximate expected

value function in two times. Firstly, we calculate an

optimal local value function for each PRU in the mis-

sion. These local functions are splitted into function

pieces. Secondly, we re-compose the value function

with all the function pieces as soon as a change occurs

at run-time. This section is divided in two parts, the

decomposition, and the recomposition. We denote as

∗

the optimal value function and V

∼

its approxima-

tion. The main objective of the recomposition is to ﬁt

∗

as good as possible.

5.1 Decomposition

The decomposition consists in the calculation of the

value functions for each PRU

in the mission. These

functions are indeed performance proﬁles (denoted as

): they indicate the expected value for this PRU if

r are allocated. Three performance proﬁles examples

are depicted in Figure 4. The PRU γ can not consume

more than 31 resource units, and give a maximum ex-

pected value of 25.

The main idea is to use these functions to re-

compose the global approximate value function. The

performance proﬁles receive a preliminary treatment.

The progressive processing provides value functions

that are similar to anytime reasoning value functions :

• they increase with the allocated resource amount,

ADAPTIVE RESOURCES CONSUMPTION IN A DYNAMIC AND UNCERTAIN ENVIRONMENT - An Autonomous

Rover Control Technique using Progressive Processing

203

f (r)

max

f (r)

max

f (r)

Figure 4: 3 PRU performance proﬁles.

• the best improvements are made with few re-

sources, the growth of V

∗

is higher at its begin-

ning than at its end.

For these reasons we split f

into i

pieces

p,1

,.. . ,g

p,i

. During the recomposition, we will take

the best pieces to re-compose the beginning of V

∼

and the worst for the end. We keep the part of f

with the best growth, i.e. the piece between (0,0)

and (r

max

p,1

, f

max

p,1

)). r

max

p,1

is the resource amount that

provides the best tradeoff between the resources spent

and the local expected value.

max

p,1

= argmax

p,r



(r)



(5)

∀i > 1,r

max

p,i

= argmax

p,r



p,i

(r)



(6)

When the ﬁrst r

max

p,1

is found, we save the ﬁrst

piece of f

as g

p,1

. We split f

in g

p,1

and f

p,2

. We

continue to search the second r

max

p,2

in f

p,2

; we save

p,2

etc... until f

p,i

is empty.

p,1



0... r

max

p,1



→ R

r → f

(r)

p,1



0... r

max

− r

max

p,1



→ R

r → f

(r − r

max

p,1

) − f

max

p,1

)

∀i > 1,

p,i



0... r

max

p,i



→ R

r → f

p,i

(r)

∀i ≥ 1,

p,i+1



0... r

max

−

∑

j=1

max

p, j



→ R

r → f

p,i

(r − r

max

p,i

) − f

p,i

max

p,i

)

(7)

Figure 5 illustrates the decomposition method for

one PRU performance proﬁle f

All PRU are treated in the same way, such that we

obtain a list of performance proﬁle pieces {g

p,i

,1 ≤

p ≤ P,1 ≤ i ≤ i

}. We sort this set with the best trade-

off criterion : g

p,i

max

p,i

)/r

max

p,i

. When this set is sorted,

the agent is ready to re-composeV

∼

f (r)

p,2

f (r) =

p,2

p,1

p,3

g (r)

f ( − r) − f ( )

pieces

performance

profile

f (r)

p,2

g (r)

max

g (r)

Figure 5: Decomposition.

5.2 Recomposition

When the mission changes during execution time, the

agent re-composes V

∼

by assembling all the pieces.

The ﬁrst g element is the one with the best growth,

and so on. The method is depicted on Figure 6. V

∼

and V

∗

have the same support [0... r

max

]. In order

to know the expected value for a given amount r, the

agent check the value V

∼

(r). Then, it will take its

local decision according to this approximate value.

performance profiles

pieces list (sorted)

r 2.r 3.r 4.r 4.r + r

1 1 1 1 1 2

...

V (r)

mission :

PRU

max max max max

r r rr

1,1 2,1 1,2 4,2

Figure 6: V

∼

recomposition.

6 VALIDATION

In the previous sections, we present how to obtain an

approximation of the value function. The rover will

use this function in order to take decision if the mis-

sion change during execution time. Now, we must

prove that :

• the time needed to obtain V

∼

is short enough,

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

204

• the rover can take good decisions by using V

∼

Concerning the time needed to calculate V

∼

, we ob-

tain very good results : it takes just few milliseconds.

Tabular 1 give computation time for different mission

sizes.

Table 1.

# PRUs 20 40 60 80 100 120 140

∗

(in s) 3 7 16 35 63 112 187

∼

(in ms) 0,4 0,9 1,2 1,7 2,2 2,6 3,5

To validate our approach, we will show that the

agent can take good decisions by using V

∼

as an ex-

pected value. The decision quality evaluation is made

throw the Q-value function comparison for each pair

(state,action) between the policies locally obtained

with V

∼

and V

∗

The validation consists in four steps :

1. we calculate both V

∼

and V

∗

2. we calculate both policies (π

∗

and π

∼

) for the cur-

rent PRU

3. we calculate Q

∗

, the local optimal Q-value func-

tion (for PRU

4. compare the loss of value while the agent is using

∼

instead of π

∗

Note that point 2 and 3 are done together at the same

time. As the MDP for PRU

has few states, the calcu-

lation of π

∗

, Q

∗

and π

∼

is quick. We did some experi-

ments with mission composed of different PRU kinds

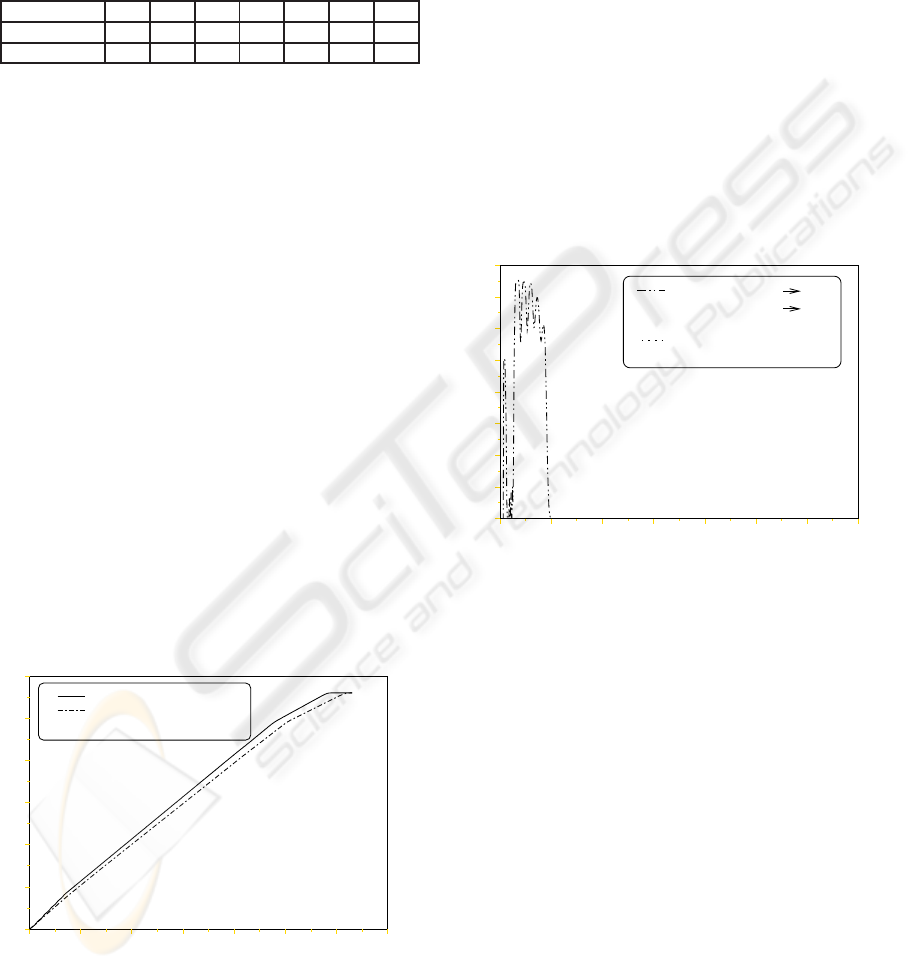
and number. Figure 7 is an example of V

∼

and V

∗

for

20 PRU with 4 PRU kinds.

0 100 200 300 400 500 600 700

100

200

300

400

500

600

Figure 7: V

∼

and V

∗

On this Figure 7 we see that V

∼

is a good approx-

imation ofV

∗

. We have done several experiments and

have obtain some good results. Q

∗

is given by the

following equation.

∗

(hr,Q,0,ℓi, E

) = V

(hr,Q,0,ℓi) (8)

∗

(hr,Q,0,ℓi, M) = V

∗

(r) (9)

It makes no sense to calculate the Q-value for π

∼

When the agent takes its decisions using π

∼

instead

of π

∗

, there may be a loss of value. The error value is

given by :

e(s) = Q

∗

(s,π

∗

(s)) − Q

∗

(s,π

∼

(s)) (10)

Indeed, if for a given state s, π

∗

(s) = π

∼

(s), then the

error is zero. Otherwise, e(s) measure the loss of

value. The objective is to obtain as few error as possi-

ble. When an error exists, the better is to have a small

value.

∆ Qe =

V : R IR

0 100 200 300 400 500 600 700

0.0

0.4

0.8

1.2

1.6

2.0

2.4

2.8

3.2

Figure 8: V

∼

and V

∗

Figure 8 is an error measure with V

∼

and V

∗

de-

picted on Figure 7. When we use our approximation

method, there is no error. It explains why we do not

see any dotted curve on the Figure. The other curve

correspondsis the error measure if the agentconsiders

that the expected value is null (V(r) = 0). When the

robot has few resources, it does not always take an

optimal decision. However, when the agent follows

our approximative policy, it never make mistakes.

Of course, this example seems to be chosen be-

cause it is the best. But it is not the case. We made

some experiments with two different PRU kinds. The

ﬁrst PRU kind is composed of tightened modules :

near qualities, near resource consumption. On the

contrary, the second PRU kind is composed of distant

modules : separate qualities, distant resource con-

sumption.

When the agent calculates π

∼

on a PRU of the ﬁrst

type, there are lots of errors. Indeed, the modules are

almost the same, so the Q-value difference between

two actions is low. Then, it is very difﬁcult for the

ADAPTIVE RESOURCES CONSUMPTION IN A DYNAMIC AND UNCERTAIN ENVIRONMENT - An Autonomous

Rover Control Technique using Progressive Processing

205

agent to take the right decision. However, in this case,

the error is also low. When the agent chooses a mod-

ule that is near of the optimal one, it does not make

the right decision, but this decision is good.

When the agent calculates π

∼

on a PRU of the sec-

ond type, there are few errors. For a given state, Q-

values are separate because the module qualities are

separate. Then, most of the time π

∼

is equal to π

∗

the robot chooses the right decision.

To conclude, if modules are clearly separate, the

robot takes the right decision. If modules are near,

the robot takes good decisions, with a low Q-value

error level.

6.1 Limits of this Approximation

Method

The resource consumption probability distribution

follows a normal distribution law in all the modules

we use for our experiments. Most of the time, it rep-

resents modules that can be found a real application.

We have also tried to make some experiments with

modules in which the resource consumption proba-

bility distribution is not normal. We made a risky

module m : the resource consumption is 4 or 16, with

P r(4|m) = 0.5 and P r(16|m) = 0.5. In this case the

module can only consume 4 or 16 units, but not 8.

In this kind of particular case V

∗

is not smooth. As

a result, V

∼

is not a good approximation. Then, π

∼

and π

∗

are different, there is a lot of error. But this

case does not represent a realistic resource consump-

tion module.

7 CONCLUSIONS

Resource consumption is crucial for an autonomous

rover. Here, this rover has to cope with limited re-

sources to executed a mission composed of hierarchi-

cal tasks. These tasks are progressiveprocessing units

(PRU). It is possible to compute an optimal resource

control for the entire mission by modelling it with an

MDP. In the case where the mission changes at exe-

cution time, the rover has to recompute online a new

global policy. We propose a way to quickly compute

an approximate value function that can be used to cal-

culate a local policy on the current PRU. MDP De-

composition and value function approximation tech-

niques are used to calculate V

∼

. We have shown in

the last section that the agent takes good decisions

when it uses V

∼

to compute its local policy π

∼

. In

a near future, we intend to complete our demonstra-

tion on real robots by considering dynamic situations

where missions can change online.

REFERENCES

Arnt, A., Zilberstein, S., Allan, J., and Mouaddib, A.

(2004). Dynamic composition of information retrieval

techniques. Journal of Intelligent Information Sys-

tems, 23(1):67–97.

Dean, T. and Lin, S. H. (1995). Decomposition techniques

for planning in stochastic domains. In proceedings

of the 14th International Joint Conference on Artiﬁ-

cial Intelligence (IJCAI), pages 1121–1127, Montreal,

Quebec, Canada.

Feng, Z., Dearden, R., Meuleau, N., and Washington, R.

(2004). Dynamic programming for structured contin-

uous markov decision problems. In proceedings of

UAI 2004, pages 154–161.

Meuleau, N., Hauskrecht, M., Kim, K., Peshkin, L., Keal-

bling, L., Dean, T., and Boutilier, C. (1998). Solving

very large weakly coupled markov decision processes.

In proceedings of the 14th Conference on Uncertainty

in Artiﬁcial Intelligence, Madison, WI.

Mouaddib, A. I. and Zilberstein, S. (1998). Optimal

scheduling for dynamic progressive processing. In

proceedings of ECAI, pages 499–503.

Parr, R. (1998). Flexible decomposition algorithms for

weakly coupled markov decision process. In proceed-

ings of the 14th Conference on Uncertainty in Artiﬁ-

cial Intelligence, Madison, WI.

Pineau, J., Gordon, G. J., and Thrun, S. (2003). Point-based

value iteration: An anytime algorithm for pomdps.

In proceedings of the 18th International Joint Con-

ference on Artiﬁcial Intelligence IJCAI, pages 1025–

1032.

Zilberstein, S., Washington, R., Berstein, D., and Mouad-

dib, A. (2002). Decision-theoretic control of planetary

rovers. LNAI, 2466(1):270–289.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

206