
SYNTHESIS
METHOD OF A PN CONTROLLER USING
FORBIDDEN TRANSITIONS SEQUENCES
R. Bekrar, N. Messai, N. Essounbouli, A. Hamzaoui and B. Riera
CReSTIC, IUT de Troyes, 9 rue de Qubec BP 396, 10026 Troyes Cedex, France
Keywords:
Forbidden state problem, Forbidden transitions sequences, Supervisory control, Discrete event systems, Petri
Nets.
Abstract:
In this paper, we propose a control synthesis method for Discrete Event Systems (DES) modelled by a bounded
ordinary Petri Nets (PN) to treat a forbidden state problem. The considered PN is transitions controllable
and contains measurable and non measurable places. The PN controller is synthesised using the forbidden
transitions sequences. The latter, are deduced from the PN reachability graph and considered as a forbidden
language generated by the PN model. To show the efficiency of the proposed method an illustrative example
is presented.
1 INTRODUCTION
In Discrete Event Systems (DES), it is important
to prevent the system to reach undesirable states.
Hence, given a DES model and a specification of
the desired behaviours, one must to synthesise an
efficient controller in order to achieve this goal.
Among tools used to synthesis a DES controller, Petri
Nets (PN) have been successfully considered as an
efficient formalism for DES control.
This paper is considered as the second phase of
our work (Bekrar et al., 2006a; Bekrar et al., 2006b)
on the identification of a DES. It allows to complete
the identified model by adding control places. Indeed,
the identified PN model can generate all the DES
states. However, it can generates, sometimes, some
states which are not observed during the system
functioning. Thus, our objective is to synthesise a PN
controller to prevent the reachability of the forbidden
states and guarantees the desired ones.
The synthesis problem of PN controllers has been
widely treated in the literature. It was introduced
either as a forbidden states problem (FSP) or a
forbidden state transitions problem (FSTP). The
synthesis methods of a PN controller allow to add a
set of control places to the initial model in order to
generate the desired behaviours. Several approaches
are suggested in order to solve this problem. Among
them we can find, the logical predicate based solu-
tions (Krogh and Holloway, 1991; Boel et al., 1995;
Holloway et al., 1996). The key idea is to perform an
off-line structural analysis for determining algebraic
expressions. The latter will be evaluated on-line for
the current marking in order to decide the firing of the
controllable transitions. These approaches are very
effective for the on-line PN control. Nevertheless,
they are valid only with a specific classes of PN.
Other approaches, which give generally nonmaxi-
mally permissive solution, have been proposed in the
literature (Giua et al., 1992; Moody and Antsaklis,
2000; Basile et al., 2006). They take the form of PN
which simplifies the analysis and the implementation
of the controller. Based on the theory of regions
many works have been developed (Ghaffari et al.,
2002; Ghaffari et al., 2003; Achour and Rezg, 2006;
Lee et al., 2006). The objective is to solve optimally
the supervisory control problem using formal and
algebraic characterisations. Finally, the PN controller
synthesis problem has been treated as integer linear
programming problem (Giua and Xie, 2004; Basile
et al., 2007a; Basile et al., 2007b). Nevertheless,
these approaches require a very high time computing.
Although the synthesis problem of PN controller
has been widely treated in the literature, the existing
approaches cannot be exploited directly in our case
because, it is impossible to characterise the forbidden
states by constraints. Indeed, the control specifica-
tion is mainly important to synthesise a controller.
However, we have neither the control specification
nor the system description because the identified
149
Bekrar R., Messai N., Essounbouli N., Hamzaoui A. and Riera B. (2008).
SYNTHESIS METHOD OF A PN CONTROLLER USING FORBIDDEN TRANSITIONS SEQUENCES.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 149-154
DOI: 10.5220/0001493201490154
Copyright
c
SciTePress

PN that we want to control is obtained using only
the measurable inputs and outputs system signals.
Let’s note that, we can determine the forbidden
states uniquely by comparing the observed system’s
states and states reachable by the identified PN model.
This paper deals with the supervisory control
problem of DES characterised by forbidden states
and modelled by bounded ordinary PN. The PN
herein considered is transitions controllable and
contains measurable and non measurable places.
The latter represent the non measurable outputs
system signals. Indeed, the fact that all transitions are
controllable then, the PN reachability graph does not
contain dangerous markings. In addition, we suppose
that we have not the control specification and the
initial marking is the unique marked state. Finally,
we consider that the PN reachability graph does
not contain deadlock states because the input and
the output signals observed during the identification
phase represent only the normal behaviours of the
considered system.
The proposed PN controller is synthesised us-
ing the forbidden transitions sequences deduced
from the PN reachability graph. The designed
PN controller permits to avoid the occurrence of
forbidden markings, generated by the non controlled
PN model, and guarantees a set of desired behaviours.
In this paper, we start by presenting the considered
FSP and defining the control specifications. Then, we
present a procedure to calculate the forbidden transi-
tions sequences from the PN reachability graph and
introduce a new algorithm to design the PN controller
using these sequences. At last, we illustrate the pro-
posed algorithm by an explicative example.
2 CONTROL SPECIFICATIONS
We consider the basic supervisory control problem to
synthesise a PN controller that avoids the occurrence
of forbidden states. In this paper, we assume that
the PN that we want to control is established using
the I/O sequences describing all the system normal
behaviours according to the algorithm presented in
(Bekrar et al., 2006b). Hence, our objective is to add
some control places in order to guarantee that all
the behaviours generated by the identified PN model
correspond to those generated by the real system.
Note also that, each PN reachable marking M
0
i
is
composed of two parts: M
0
i
=
·
M
0
im
M
0
i ¯m
¸
where, the first
one represents the marking of the measurable places
and the second part represents the estimated marking
of the non measurable places.
The control specifications to be addressed in this
paper are the forbidden states type and the problem
herein considered becomes a FSP. We will treat it as
a FSTP as proved in (Ghaffari et al., 2002). To solve
this problem, we propose an algorithm that consists
in: (1) identifying the set of the forbidden markings,
(2) determining the set of the equivalent forbidden
state transitions, (3) developing a PN controller.
2.1 Identification of Forbidden
Markings
Contrary to works proposed to treat the FSP where
the forbidden states are defined explicitly by con-
straints, in our case we must calculate them using the
behaviours of the real system and those of the PN
model. The behaviours of the considered system are
represented by the set of its reachable states called
E . Those generated by the PN modelling the system
are represented by its reachability graph called R
0
G
.
Note that, a marking M
0
i
∈ R
0
G
reachable by the PN
that we want to control is said forbidden marking if
its measurable part is not equivalent to any state E
i
in E otherwise, it is a legal marking. Hence, the set
of the forbidden markings can be obtained using the
following procedure:
Input: E and R
0
G
.
Output: M
f r
the set of forbidden markings.
Begin
1. Initialise the set of forbidden markings: M
f r
:=
/
0.
2. For each marking M
0
i
∈ R
0
G
do:
(a) If there exists a state E
i
∈ E such that M
0
im
= E
i
then:
• M
0
i
is legal marking.
(b) Else, M
0
i
is a forbidden marking.
• Update the set of forbidden markings: M
f r
:=
M
f r
∪ M
0
i
.
End If.
End For.
End.
Once the set of the forbidden markings is obtained,
we should determine the set of the transitions lead-
ing to or firing from forbidden markings in order to
prevent the firing of these transitions.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
150

2.2 Forbidden State Transitions
A state transition in the reachability graph of the PN
that we want to control, which fires from a marking
M
0
i
∈ R
0
G
and leads to a marking M
0
j
∈ R
0
G
(M
0
i
[t
i
> M
0
j
),
is said forbidden state transition if and only if one of
the following conditions is verified:
• (a) M
0
i
is forbidden marking or,
• (b) M
0
j
is forbidden marking.
These can be reformulated, using E and R
0
G
, as fol-
lows: a state transition (M
0
i
t
i
→ M
0
j
) in R
0
G
is said for-
bidden iff:
• ∃E
i
∈ E : M
0
im
= E
i
and @E
j
∈ E : M
0
jm
= E
j
or,
• @E
i
∈ E : M
0
im
= E
i
and ∃E
j
∈ E : M
0
jm
= E
j
or,
• @E
i
, E
j
∈ E : M
0
im
= E
i
and M
0
jm
= E
j
.
Proof : the occurrence of forbidden marking can be
prevented by avoiding the firing of the transition
leading to this marking. Moreover, it is clear that
a transition firing from a forbidden marking is a
forbidden transition. So, each transition leading to
or firing from a forbidden marking is considered as a
forbidden transition.
Therefore, the forbidden state transitions set can be
obtained using the following procedure:
Input: E , R
0
G
and M
f r
.
Output: Ψ the set of forbidden state transitions.
Begin
1. Initialise the set of forbidden state transitions:
Ψ =
/
0.
2. For each state transition (M
0
i
t
i
→ M
0
j
) ∈ R
0
G
such
that M
0
i
, M
0
j
∈ R
0
G
do:
• If (a) or (b) is verified then: (M
0
i
t
i
→ M
0
j
) is a
forbidden state transition.
– Update Ψ:(Ψ:= Ψ ∪ {(M
0
i
t
i
→ M
0
j
)}).
• Else, (M
0
i
t
i
→ M
0
j
) is a legal state transition.
End If.
End For
End.
Once the forbidden state transitions are determined,
the forbidden transitions sequences will be calculated
and used for designing a PN controller. More details
concerning these steps will be presented in the next
section.
3 THE PROPOSED PN
CONTROLLER
We can solve the forbidden state problem considered
in this paper by adding control places {p
c1
, ..., p
ck
}
to the initial PN model (N, M
0
0
). These places are
defined as follows:
Definition 1: A control place p
ci
of a PN model
(N, M
0
0
) is defined by: (i) M
0
0
(p
ci
): its initial marking,
(ii) Post(p
ci
, .) and Pre(p
ci
, .): the weighting vectors
of the arcs connecting the transitions of (N, M
0
0
) to
p
ci
and connecting p
ci
to the transitions of (N, M
0
0
)
respectively.
Remark 1: Since the considered PN is ordinary then,
the arcs weighting values are equal to 1.
In order to solve this problem, we propose to use the
forbidden transitions sequences, calculated from the
reachability graph of the PN that we want to control,
to determine the control places to be added. Note
that, these sequences have been used by Lee et al.,
(2006) but with the constraint asynchronous reacha-
bility graph.
3.1 The Forbidden Transitions
Sequences
Before introducing the computing procedure of the
forbidden transitions sequences, let us present the
following definitions that will be used in the PN
controller design algorithm.
Definition 2: A transitions sequence σ
i
is said forbid-
den if and only if it allows the firing of at least one
forbidden transition. Thus, σ
i
= t
1
,t
2
, ..., t
k
,t
l
, ..., t
f
is said forbidden iff: ∃t
i
∈ σ
i
:
∗
M(t
i
) ∈ M
f r
or
M
∗
(t
i
) ∈ M
f r
where
∗
M(t
i
) and M
∗
(t
i
) represent
respectively the input and the output marking of t
i
in
R
0
G
, otherwise, it is a legal.
The forbidden transitions sequences are calculated
using the PN reachability graph as follows:
Input: R
0
G
, Ψ.
Output: S the set of forbidden transitions sequences.
Begin
1. Initialise the set of forbidden transitions se-
quences: S :=
/
0.
2. Calculate S
0
the set of all legal transitions se-
quences reachable from the initial marking M
0
0
.
3. Calculate the set of the successors transitions of
each transitions sequence σ
i
in S
0
, noted Suc(σ
i
).
4. For each transition t
i
in the set Suc(σ
i
) do:
SYNTHESIS METHOD OF A PN CONTROLLER USING FORBIDDEN TRANSITIONS SEQUENCES
151
(a) If t
i
is a forbidden transition then:
• σ
j
:= σ
i
t
i
is a forbidden transitions sequence.
• Else, stop the successors computation proce-
dure of the transitions sequence σ
j
.
(b) Update S (S := S ∪{ σ
j
}).
End If.
End For
5. Calculate the set of successors transitions of each
transitions sequence σ
i
in S.
6. Go to 4.
7. End.
Note that, in our case, each forbidden transitions se-
quence σ
i
is composed of two sub-sequences as fol-
lows: σ
i
= t
1
, ..., t
k
| {z }
σ
00
i
|t
l
, ..., t
f
| {z }
σ
in
i
, with σ
00
i
is a legal tran-
sitions sub-sequence authorised to be fired from the
initial marking M
0
0
and it can be equal to the empty
string ε (i.e., σ
00
i
= ε). Thus, it means that there exists
forbidden states reachable from M
0
0
after the firing of
only one transition. σ
in
i
is a sub-sequence forbidden
to firing from M
0
k
where M
0
k
is the marking reachable
after the firing of t
k
. This sub-sequence represents
the transitions influenced by the firing of the forbid-
den transition t
l
. We note by
∗
σ
in
i
and σ
in∗
i
the first
and the last transition of σ
in
i
respectively. Hence, all
the markings reachable from M
0
0
after the firing of the
sub-sequence σ
00
i
, transition after transition, are legal
markings. However, the markings reachable from M
0
k
after the firing of the sub-sequence σ
in
i
, transition af-
ter transition, are forbidden markings as represented
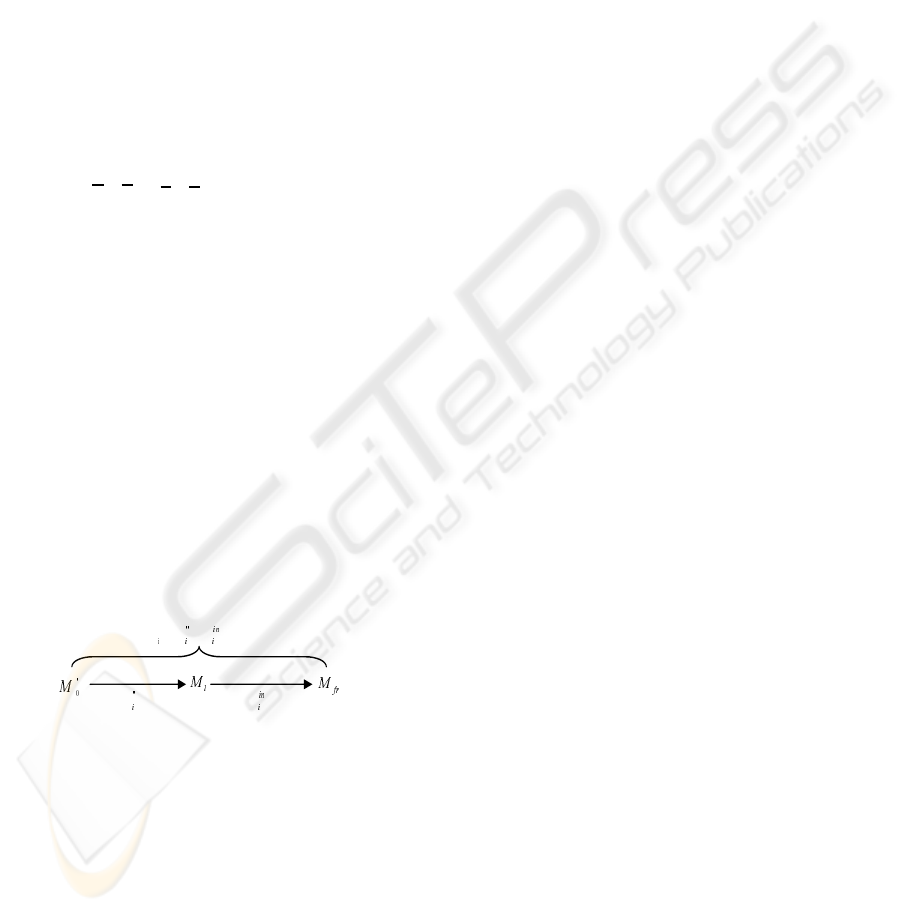
in figure 1.
σ
σ
σ σ σ
= +
Figure 1: Legal and forbidden markings.
Definition 3: Let’s σ
i
= t
1
,t
2
, ..., t
k
transitions se-
quence. |σ
i
| designs the length of this sequence,
and it represents the number of transitions in this
sequence.
Remark 2: For each transition t
i
∈ σ
i
, we note by
|t
i
∩ σ
i
| the number of times that the transition t
i
appears in σ
i
.
Definition 4: Let’s σ
i
= t
1
,t
2
, ..., t
k
a transitions
sequence that we consider as a word generated by a
PN. The prefix of σ
i
, noted Pre f (σ
i
), is a word t
1
...t
j
with 0 ≤ j ≤ k and k = |σ
i
|. For q ∈ N: Pre f (σ
i
)
(q)
represents a prefix of σ
i
of width equal to q.
Remark 3: Since PN to be controlled is bounded, then
its reachability set is finite. Also, the language gener-
ated by this PN is finite prefix-closed language.
3.2 Synthesis Algorithm of PN
Controller
Based on previous definitions and notations, we pro-
pose an algorithm that allows to add control places
to the initial PN model for preventing the reachability
of forbidden markings. This algorithm contains the
following:
1. Construction of the reachability graph of the PN
that we want to control.
2. Identification of the forbidden markings and the
determination of the forbidden state transitions by
browsing the PN reachability graph.
3. Determination of the forbidden transitions se-
quences set. These latter, we consider them as for-
bidden words generated by the PN model. Then,
we use these sequences to synthesise a PN con-
troller.
Hence, the PN controller will be synthesised using
the following algorithm:
Input: E the system states set, (N, M
0
0
) the PN model.
Output: Controlled PN.
Begin
1. Construct the reachability graph R
0
G
of the PN
model to be controlled (N, M
0
0
).
2. Identify the set of forbidden markings noted M
f r
as introduced in subsection 2.1.
3. Determine the set of forbidden state transitions Ψ
by executing the procedure described in subsec-
tion 2.2.
4. Determine the set S of all forbidden transitions
sequences firing from the initial marking M
0
0
by
browsing the reachability graph of PN that we
want to control as shown in subsection 3.1.
5. Update the set of forbidden transitions sequences
S as follows:
(a) For each transitions sequence σ
i
∈ S do:
i. Calculate the prefix set of this sequence noted
Pre f (σ
i
).
ii. Compare the prefixes of σ
i
to the prefixes of
all the transitions sequences in S as follows:
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
152
A. If there exists at least one transitions se-
quence σ
j
such that, all the elements of pre-
fixes set of σ
i
are included in the prefixes set
of σ
j
(Pre f (σ
i
) ⊂ Pre f ()σ
j
) then:
• Eliminate σ
i
from S: S := S\{σ
i
}
B. Else, σ
i
still in S.
End If
End For.
6. For each forbidden transitions sequence in S do:
(a) Determine the sub-sequence of legal transitions
σ
00
i
and the sub-sequence of forbidden transi-
tions σ
in
i
.
(b) For each sub-sequence of forbidden transitions
σ
in
i
, we determine
∗
σ
in
i
and σ
in∗
i
.
(c) Add a control place p
ci
as an input of
∗
σ
in
i
and
as an output of σ
in∗
i
.
(d) Mark p
ci
with initial marking M
c0
(p
ci
) =
|
∗
σ
in
i
∩ σ
00
i
|. Il there exists several forbidden
transitions sub-sequences which have the same
∗
σ
in
i
and σ
in∗
i
then, we add one control place
p
ci
and we mark it with initial marking equal to
max
i,σ
i
∈S
(|
∗
σ
in
i
∩ σ
00
i
|).
End For.
End.
This algorithm allows to complete the PN model,
established using the identification approach pro-
posed previously, by adding control places. The anal-
ysis of the algorithm computational complexity shows
that it is linear with the number of places, of transi-
tions and, the length of the largest forbidden transi-
tions sequences.
4 ILLUSTRATIVE EXAMPLE
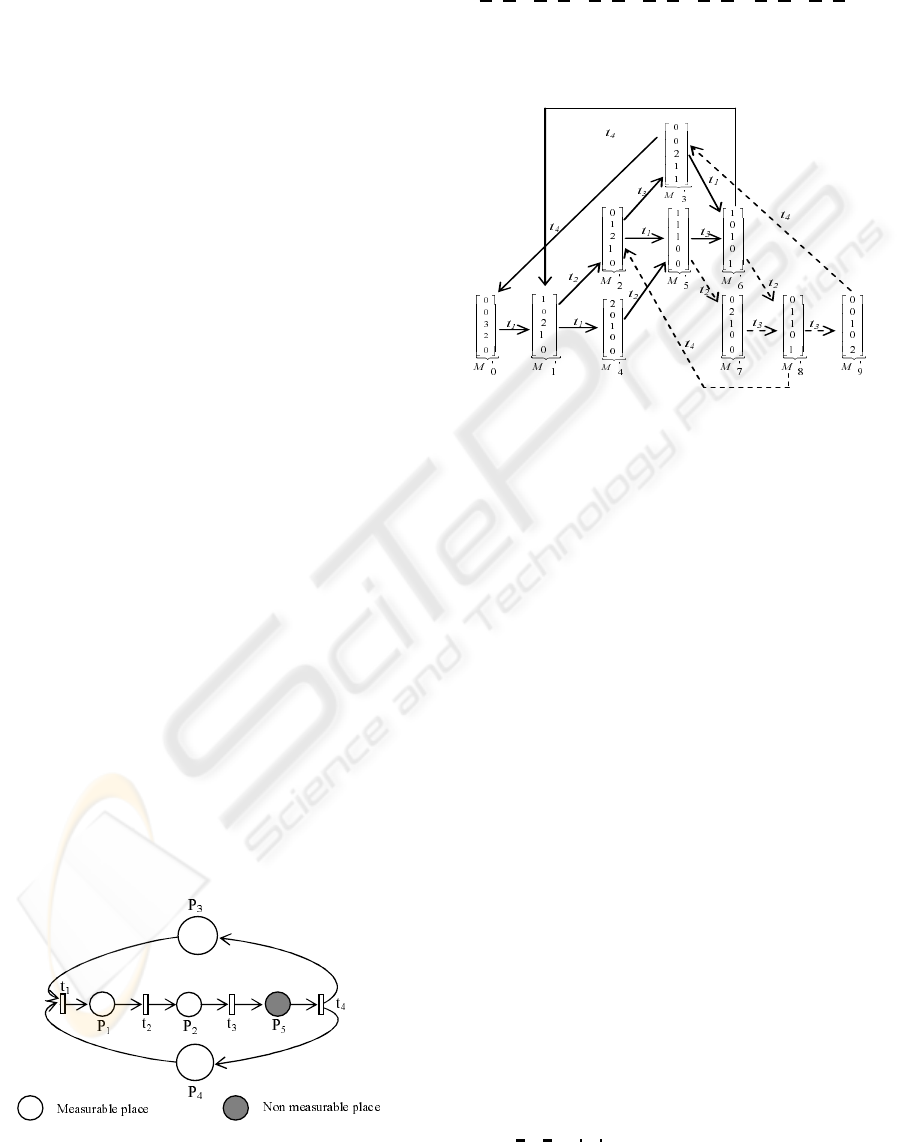
To illustrate the proposed algorithm, let us consider
the example of a system described by the identified
PN model of figure 2:
••
••
•
Figure 2: The PN model.
The set of its states is given by: E =
½
0
0
3
2
| {z }
E
0
,
1
0
2
1
| {z }
E
1
,
0
1
2
1
| {z }
E
2
,
0
0
2
1
| {z }
E
3
,
2
0
1
0
| {z }
E
4
,
1
1
1
0
| {z }
E
5
,
1
0
1
0
| {z }
E
6
¾
.
Firstly, we elaborate the PN reachability graph that is
given in figure 3.
Figure 3: The PN reachability graph.
The set of forbidden markings is: M
f r
=
{M
0
7
, M
0
8
, M
0
9
}. These markings must be removed
from R
0
G
together with their arcs coming from other
markings to these forbidden markings or going from
these forbidden markings to other markings in R
0
G
.
The set of the equivalent forbidden state transi-
tions are: {(M
0
5
t
2
→ M
0
7
), (M
0
7
t
3
→ M
0
8
), (M
0
8
t
2
→ M
0
9
),
(M
0
9
t
4
→ M
0
3
), (M
0
6
t
2
→ M
0
8
), (M
0
8
t
4
→ M
0
2
)}. By ap-
plying the procedure described in subsection 4.1,
the forbidden transitions sequences firing from the
initial marking are: σ
1
= t
1
t
2
t
3
t
1
t
2
, σ
2
= t
1
t
2
t
3
t
1
t
2
t
4
,
σ
3
= t
1
t
2
t
3
t
1
t
2
t
3
, σ
4
= t
1
t
2
t
3
t
1
t
2
t
3
t
4
, σ
5
= t
1
t
1
t
2
t
3
t
2
,
σ
6
= t
1
t
1
t
2
t
3
t
2
t
4
, σ
7
= t
1
t
1
t
2
t
3
t
2
t
3
, σ
8
= t
1
t
1
t
2
t
3
t
2
t
3
t
4
,
σ
9
= t
1
t
1
t
2
t
2
, σ
10
= t
1
t
1
t
2
t
2
t
3
, σ
11
= t
1
t
1
t
2
t
2
t
3
t
4
,
σ
12
= t
1
t
1
t
2
t
2
t
3
t
3
, σ
13
= t
1
t
1
t
2
t
2
t
3
t
3
t
4
. Thus, the
set of the forbidden transitions sequences is
S = {σ
i,i=1,...,13
}. To update S, we must calcu-
late the prefix of each sequence in S. We take as
example the sequences σ
1
and σ
2
: Pre f (σ
1
) =
{ε,t
1
,t
1
t
2
,t
1
t
2
t
3
,t
1
t
2
t
3
t
1
,t
1
t
2
t
3
t
1
t
2
}, Pre f (σ
2
) =
{ε,t
1
,t
1
t
2
,t
1
t
2
t
3
,t
1
t
2
t
3
t
1
,t
1
t
2
t
3
t
1
t
2
,t
1
t
2
t
3
t
1
t
2
t
4
}. We
note that Pre f (σ
1
) = Pre f (σ
2
) then, we eliminate σ
1
from S: S := S\{σ
i
}. By repeating the same process
with the remaining sequences, and after updating
S, we have finally : S = {σ
2
, σ
4
, σ
6
, σ
8
, σ
11
, σ
13
}.
Then, for each forbidden transitions sequence in
S we determine the legal transitions sub-sequence
and the forbidden one. We take for example
σ
8
= t
1
t
1
t
2
t
3
| {z }
σ
00
8
|t
2
t
3
t
4
|{z}
σ
in
8
. We remark that σ
00
8
= t
2
and
SYNTHESIS METHOD OF A PN CONTROLLER USING FORBIDDEN TRANSITIONS SEQUENCES
153
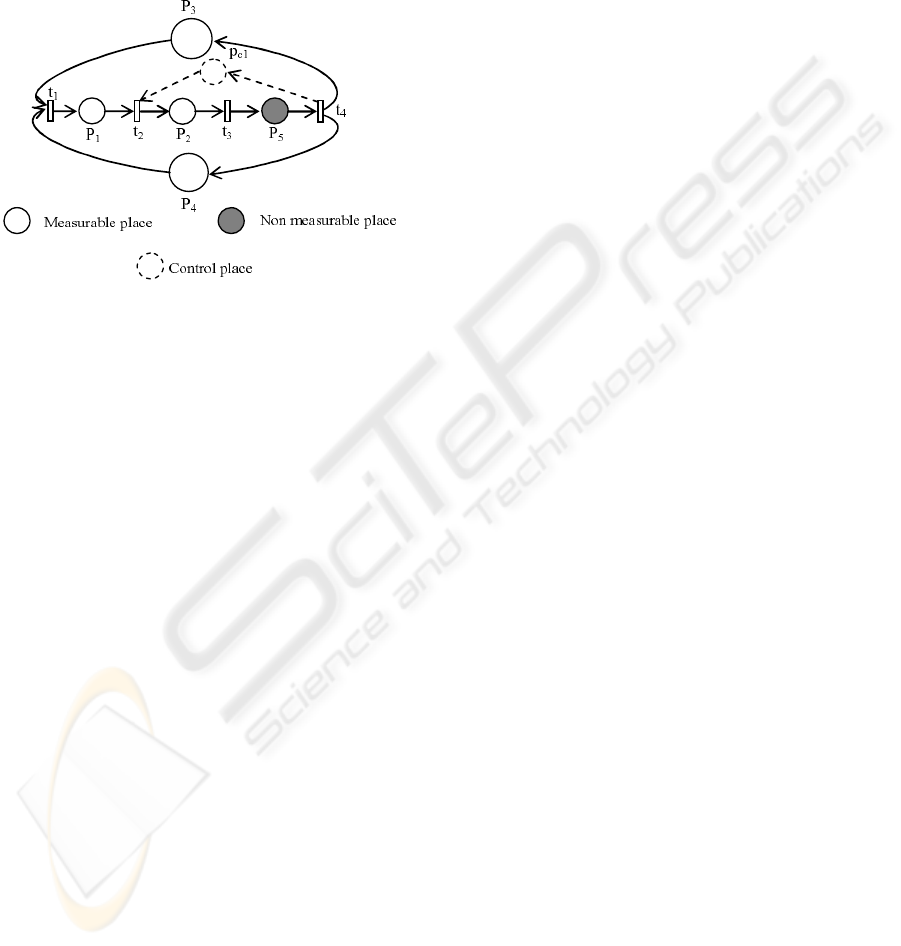
σ
in
8
= t
4
. Finally, by analysing the remaining for-
bidden sequences, we see that all the forbidden
transitions sub-sequences have the same
∗
σ
in
i
= t
2
and σ
in∗
i
= t
4
for i ∈ {2, 4, 6, 11, 13}. Therefore,
we add one control place p
c1
with initial marking
M
oc
(p
c1
) = max(|
∗
σ
in
i
∩ σ
00
i
|) = 1. This place is an
input of t
2
and an output of t
4
as depicted in the figure
4.
•
•
•
•
•
•
Figure 4: The Controlled PN model.
5 CONCLUSIONS
This paper presents a synthesis method of a PN con-
troller to solve a FSP of DES modelled by a bounded
ordinary PN. The model to be controlled is transi-
tions controllable. Using the system behaviours and
those generated by the considered PN model, forbid-
den markings are identified and the equivalent forbid-
den state transitions are determined. Then, the forbid-
den transitions sequences deduced from the PN reach-
ability graph are used to synthesise a PN controller.
The latter is maximally permissive within the specifi-
cations that guarantees the desired behaviours.
As Future work, we will generalise this method to PN
with uncontrollable transitions.
REFERENCES
Achour, Z. and Rezg, N. (2006). Time floating general mu-
tual exclusion constraints (tfgmec). In IMACS, Multi-
conference on Computational Engineering in Systems
Applications.
Basile, F., Carbone, C., and Chiacchio, P. (2007a). Feed-
back control logic for backward conflict free choice
nets. In IEEE Transaction on Automation and Con-
trol.
Basile, F., Chiacchio, P., and Giua, A. (2006). Suboptimal
supervisory control of Petri nets in presence of uncon-
trollable transitions via monitor places. In Automat-
ica.
Basile, F., P.Chiacchio, and Giua, A. (2007b). An optimi-
sation approach to Petri net monitor design. In IEEE
Transaction on Automation and Control.
Bekrar, R., Messai, N., Essounbouli, N., Hamzaoui, A., and
Riera, B. (2006a). Identification of discrete event sys-
tems using ordinary Petri nets. In IAR-ACD’06, Pro-
ceeding of 2006 Workshop on Advanced Control and
Diagnosis.
Bekrar, R., Messai, N., Essounbouli, N., Hamzaoui, A., and
Riera, B. (2006b). Off-line identification for a class of
discrete event systems using safe Petri nets. In DES-
Des’06, 3rd IFAC Workshop on Discrete Event System
Design.
Boel, R., Ben-Naoum, L., and Breusegem, V. V. (1995). On
forbidden state problems for a class of controlled Petri
nets. In IEEE Transaction on Automatic and Control.
Ghaffari, A., Rezg, N., and Xie, X. (2002). Algebraic and
geometric characterization of Petri net controllers us-
ing the theory of regions. In WODES’02, Proceedings
of 6
th
Worksop on Discrete Event Systems.
Ghaffari, A., Rezg, N., and Xie, X. (2003). Feedback
control logic for forbidden state problems of marked
graphs: application to a real manufacturing system. In
IEEE transaction on Automatic and Control.
Giua, A., DiCesare, F., and Silva, M. (1992). Generalized
mutual exclusion constraints on nets with uncontrol-
lable transitions. In Proceedings of IEEE Interna-
tional Conference on System, Man and Cybernitic.
Giua, A. and Xie, X. (2004). Control of safe ordinary Petri
nets with marking specifications using unfolding. In
WODES’04, Proceedings of the 7
th
IFAC Workshop
on Discrete Event Systems.
Holloway, L., Guan, X., and Zhang, L. (1996). A general-
ization of state avoidance policies for controlled Petri
nets. In IEEE Transaction on Automatic and Control.
Krogh, B. H. and Holloway, L. E. (1991). Synthesis of feed-
back control logic for discrete manufacturing systems.
In Automatica.
Lee, E. J., Toguyeni, A., and Dangoumau, N. (2006). A
Petri net based approach for the synthesis of parts’
controllers for reconfigurable manufacturing systems.
In Proceeding of SICE-ICASE International Joint
Conference.
Moody, J. and Antsaklis, P. (2000). Petri net supervisors for
dbs with uncontrollable and unobservable transitions.
In Proceedings of IEEE International Conference on
System, Man and Cybernitic.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
154
