ALTITUDE CONTROL OF SMALL HELICOPTERS USING A

PROTOTYPE TEST BED

Nikos I. Vitzilaios and Nikos C. Tsourveloudis

Intelligent Systems & Robotics Laboratory, Technical University of Crete, Chania, Greece

Keywords: Unmanned Helicopters, Experimental Test Bed, Altitude Control, Fuzzy Control, Aerial Robotics.

Abstract: In this paper we present an experimental test bed for the development and evaluation of control systems for

unmanned helicopters. The test bed consists of a small unmanned helicopter, mounted on a flying stand that

permits all possible movements but prevents the helicopter from damaging or crashing. A fuzzy controller is

developed in MATLAB and tested in the helicopter using the test bed. The controller is able to perform

hovering and altitude control. Experimental results are presented for various test cases.

1 INTRODUCTION

Unmanned helicopters are the most flexible flying

machines among the variety of UAVs (Unmanned

Aerial Vehicles), since they have the ability to take

off and land vertically as well as to perform

aggressive maneuvers and hovering, which gives

them the advantage of effective observation from

various positions. These advantages along with the

continuous development of robotic vehicles’

technology have led to the use of unmanned

helicopters in many applications, both civil and

military, such as surveillance, traffic management,

land management, border patrol, and search and

rescue missions. As a result, there has been

remarkable growth in the market of unmanned

helicopters (aka VTOL UAVs for Vertical Take-Off

and Landing UAVs), which nowadays includes

vehicles of various types, sizes and operational

capabilities (Spanoudakis et al., 2003). During the

last years, small scale (about 1500 mm in length)

helicopters are preferred for development and

experimentation due to their low cost and

expendability.

Although small scale unmanned helicopters offer

as experimentation platforms the advantages of low

cost and easy operation, the development of

autonomous navigation systems for such vehicles is

a difficult and dangerous procedure that may

increase this overall cost, since except from the

equipment needed (helicopter, sensors, telemetry

systems etc) one should add the cost of crashes and

damages that may occur during experimentation.

Since helicopters are very unstable and difficult to

control, experimentation on real vehicles often result

in damaging accidents. For this reason, the

development of an autonomous navigation controller

begins with numerous tests in a software-based

simulation environment. In this environment,

controllers are evaluated for their ability to control

efficiently the helicopter. If the simulation results

are encouraging, the controller may be tested on the

real vehicle.

The simulation procedure has drawbacks as well.

At first, the simulation environment cannot imitate

helicopter’s navigation in detail with all possible

environmental disturbances. Therefore, a controller

that seems to work satisfactorily in the simulation

may be insufficient for the navigation of the real

vehicle in a real environment. Moreover,

independently of any simulation evaluation,

first/initial tests with a real vehicle generally are the

most dangerous, since a lot of unexpected problems

may arise at this time. As a result, it would be

desirable to test the controller on a real vehicle but

in a safe environment, without having the danger of

crashing and destroying the equipment or harm

people that monitor the flight.

In the past years, there have been proposed ways

of testing controllers on a real vehicle safely.

Normally there is a mechanical construction where a

real helicopter (or a simplified model of it) can fly

indoors without crashing or harming the humans

involved in the experimentation.

In the literature we meet constructions that

simulate a real helicopter. In (Tanaka, Ohtake, and

I. Vitzilaios N. and C. Tsourveloudis N. (2008).

ALTITUDE CONTROL OF SMALL HELICOPTERS USING A PROTOTYPE TEST BED.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 77-84

DOI: 10.5220/0001493600770084

 SciTePress

Wang, 2004), a custom helicopter-like construction

whose degrees of freedom are reduced, is used for

the design and evaluation of a flight stabilization

controller. In (Andrievsky, Peaucelle, and Fradkov,

2007), a mechanical construction is used to emulate

the flying behavior of a helicopter. The experimental

setup consists of a base on which a long arm is

mounted that carries the helicopter body. Two

motors with propellers mounted on the helicopter

body can generate the force that causes the

helicopter body to lift off the ground. A similar test

bed is also used in (Kutay et al., 2005).

Further in the literature, we meet systems that use

real helicopters for the experiments. In (Dzul,

Lozano, and Castillo, 2004) and (Mancini et al.,

2007), a mechanical construction holds the

helicopter in a stable position allowing only small

and safe movements. Using mechanical limitations,

the helicopter is able to move in only one or two

axes and within limits. As a result the helicopter

cannot take any dangerous orientation or collide to

the ground.

The drawback of the work presented in the above

references, is that either a helicopter emulation

construction is used, or a real helicopter with

reduced degrees of freedom. In both cases, the

developed controller partially covers the control of

the vehicle in one or two axes and it is not sufficient

to fully control a helicopter in real conditions. The

motivation of this paper is the construction of a

laboratory test bed where small helicopters can be

safely (for both humans and the equipment involved)

used indoors for experimental validation without

limitations in helicopter’s movement. Indoor flying

gives the ability for continuous tests regardless of

weather conditions. Moreover, the suggested setup

minimizes the need for experienced helicopter pilots

within the research group. Flying small helicopters

requires pilot training which stems research efforts

towards autonomous helicopter flights.

In this paper we propose a fuzzy controller for the

altitude and hovering control of an unmanned

helicopter. The controller is developed using the

proposed test bed and is able to stabilize the

helicopter in desired positions (each position is

defined by horizontal and vertical coordinates).

Except from hovering at a desired altitude, the tasks

of autonomous take-off and landing are also

considered here.

In the literature there is previous work on the

autonomous altitude control of unmanned

helicopters. Usually altitude control is a part of an

autonomous navigation controller (Shin et al., 2005),

(Kim and Shim, 2003), where a subsystem dedicated

to altitude control cooperates with other subsystems

in order to navigate the helicopter. In (Kim et al.,

2004) an adaptive approach is proposed for altitude

control for an unmanned helicopter which utilizes

rotor RPM to track altitude commands. Significant

work has been done also in the field of autonomous

landing problem for unmanned helicopters

(Sapiralli, Sukhatme, and Montgomery, 2002),

(Merz, Duranti, and Conte, 2006).

This paper is organised as follows. In Section 2

we present the experimental test bed that we use in

order to develop the controller. Main parts and

systems of the test bed are presented as well as the

way this test bed works. In Section 3 we present a

fuzzy controller able to control the altitude of the

helicopter and perform hovering at a stable desired

position. In Section 4, experimental results are

presented and remarked. At last, a conclusion is

derived as well as future work on the subject is

suggested.

2 EXPERIMENTAL TEST BED

The laboratory test bed consists of three basic

elements; a customized flying stand, a customized

helicopter and a ground control station (Figure 1).

Helicopter with Avionics

Flying Stand

Control Station

Figure 1: View of the experimental test bed.

2.1 Helicopter Flying Stand

Helicopter flying stand is a mechanical construction

able to hold the helicopter, allowing full movements

(6 degrees of freedom) while protecting it from

damaging and crashing. It is a customized

construction based on a commercially available

flying stand that it is used by inexperienced pilots

for flight training.

The stand allows the helicopter move naturally

without any constraint around a 2.1m diameter circle

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

(Figure 6), flying forwards, backwards or sideways.

A gas strut is used to counterbalance the weight of

the stand. As a result the helicopter does not lift any

extra weight. In Figure 2, rotations as well as the

Euler angles of the helicopter are presented.

Since the test bed will be used for indoor

experiments, a positioning system must be

developed in order to know helicopter’s position

during testing. To avoid high cost indoor positioning

and localization systems, we utilize the rotary

movement of the central shaft of the stand. The

stand and consequently the helicopter move around a

circle (planar rotation at Figure 2, Figure 6) with a

rotation angle which may easily be monitored. For

this reason, we put a rotation encoder on the central

shaft of the stand (Figure 3). The encoder initializes

its position to zero and then gives signed numbers

that denote the current position relative to the initial

position. Positive numbers denote rotation to the left

while negative numbers denote rotation to the right

side. The rotation encoder gives the planar position

of the helicopter at each time instant.

Roll

Pitch

Planar

Rotation

Elevation

Rotation

Yaw

Figure 2: Euler angles and rotation axes.

Moreover, we need to know the altitude in which

the helicopter flies. The flying stand gives the ability

to the helicopter to fly at a maximum height of

60cm. An infrared sensor is used to monitor the

actual value of altitude. The sensor is mounted at the

lower part of the bracket that holds the helicopter, as

it is shown in Figure 3. The accuracy of the altitude

readings is less than 1cm, which is far better than the

accuracy of outdoor altimeters or GPS.

Rotation

Sensor

Altitude

Altitude Sensor

Figure 3: Positioning sensors.

2.2 Helicopter and Avionics

The VTOL that we use in our test bed is a

customization of a 50-size (1200 mm length, 405

mm height, 1350 mm main rotor diameter)

commercially available electric powered RC

helicopter. An important characteristic of this

helicopter is that it has electric motor so there is no

need for fuel gas, and therefore it does not produce

any exhaust gasses during its operation, which is

important for indoor testing. This helicopter has

been heavily customized in order to be ready for

experimental use. In what follows we describe the

additional equipment and avionics we have put on

board.

2.2.1 Inertial Measurement Unit (IMU)

This unit gives the orientation of the helicopter. The

unit consists of 3D gyroscopes, accelerometers and

magnetometers and outputs the 3 Euler angles (roll,

pitch and yaw). The IMU used is the commercial

MTi model of Xsens Motion Technologies. For the

communication between IMU and control station a

USB-serial data and power cable is used.

2.2.2 Digital Switch

This is the interface that manages the switching from

manual to autonomous flight. Manual flight is

controlled remotely by a human operator, while

autonomous flight is supervised by a Central

Processing Unit (CPU). Switching between manual

and autonomous flight is an important operation

because it allows the human tester to regain manual

control at any time instant during experimentation,

which is very useful in case of failure or insufficient

controller behaviour.

ALTITUDE CONTROL OF SMALL HELICOPTERS USING A PROTOTYPE TESTBED

2.2.3 Servo Driver/Controller

RC servos are the actuators used to control the

motion of the helicopter. In manual operation, the

onboard receiver forwards the transmitter commands

to servos by sending appropriate PWM signals. In

order to send such signals from the control station to

the servos, a servo driver is needed. For that reason a

PIC microcontroller is used, which translates control

signals from the ground station to RC PWM servo

signals and drives the servos. Further, the PIC reads

the input from the localization system (x-y position,

altitude) and transmits it to the control station.

2.2.4 Communication System

A wireless communication system has been

established between the control station and the PIC

microcontroller. Having 2 receiver/transmitter units

(one on the helicopter and one on the ground station)

and by using the Bluetooth protocol, we obtain two-

way communication between the serial port of the

PIC and the serial port of the control station.

2.2.5 Power System

The electric helicopter has high power consumption.

During hovering, the electric motor needs about 50A

current of 25V. Normally in these helicopters, LiPo

batteries are used that have high capacity and the

ability to sustain big currents. With this consumption

and with a high capacity LiPo battery, the helicopter

can perform hovering for about 15 minutes. To

overcome this limitation in the duration of

experiments, the test bed is provided with constant

power supply of 24V that gives continuous current

to the helicopter.

2.3 Ground Control Station

Since our test bed works indoor and we can have all

the signals through wireless communication (expect

from the IMU), there is no need to put any processor

unit onboard. For this reason we use portable CPU

which serves as the “control station”. Because of this

solution, the helicopter has fewer payloads to lift,

while the control station has increased processing

power able to run control algorithms at high speeds.

In Figure 4 a block diagram presents the

connections of the equipment and the data

transmission through these connections, for each

subsystem (flying stand, helicopter and control

station).

Figure 4: System Architecture.

3 ALTITUDE & HOVERING

CONTROL

The controller developed and tested in the test bed is

a fuzzy controller for altitude and hovering control.

The objective of the controller is to hold stable the

helicopter at a predefined horizontal position and

altitude.

Roll Angle

Position Error

Altitude Error

Rule Base

-150 -100 -50 0 50 100 150

0.2

0.4

0.6

0.8

angle-error

Degree of

membership

LB L Zero R RBLS RS

-150 -100 -50 0 50 100 150

0.2

0.4

0.6

0.8

angle-error

Degree of

membership

LB L Zero R RBLS RS

-150 -100 -50 0 50 100 150

0.2

0.4

0.6

0.8

angle-error

Degree of

membership

LB L Zero R RBLS RS

Aileron

Throttle

Elevator

Change of

Position Error

Pitch Angle

0 0.1 0.2 0.3 0.4 0.5 0. 6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

Front-C

Degree of m embe rship

N-P H

0 0. 1 0.2 0.3 0.4 0.5 0. 6 0. 7 0.8 0.9 1

0.2

0.4

0.6

0.8

Front-C

Degree of membership

N-P H

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

Front-C

Degree of membership

N-P H

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

Front-C

Degree of membership

N-P H

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

Front-C

Degree of membership

N-P H

Figure 5: Hovering and Altitude Fuzzy controller.

3.1 Fuzzy Controller

A fuzzy controller of the Mamdani type has been

designed and implemented (Figure 5) in the

MATLAB environment. The objective of this

controller is to keep the helicopter “hovering” at

predefined positions subject to wind and other

disturbances.

As shown in Figure 5, the inputs of the fuzzy

controller are the roll and pitch angles of the

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

helicopter at every time instant, as well as the

position error, the change of position error and the

altitude error. In Figure 6 we show the

representation of the position error input, which is

defined as the difference between the current

horizontal position and the target horizontal position.

Position Error

Target

1.05m

Figure 6: Position error representation.

As position error represents how far the

helicopter is from the target point, the change of

position error represents the way that position error

changes and if the helicopter reaches the target point

or moves away from it. The altitude error is also

calculated as the difference between the current and

the target altitude. The outputs of the controller are

the change of the roll and pitch angles (aileron and

elevator variables respectively), as well as the

change in the throttle of the helicopter.

Roll angle is given by the IMU in real time.

Although the flying stand permits roll angles from

-30

to 30

, the flight control system takes as input

degrees from -90

to 90

. The linguistic variables

that represent the roll angle are: left big (LB), left

(L), zero (ZERO), right (R), right big (RB), and their

membership functions are shown in Figure 7.

The second input variable is the pitch angle of the

helicopter. The linguistic variables for this input are:

back big (BB), back (B), zero (ZERO), front (F),

front big (FB), with membership functions also

presented in Figure 7.

The third input variable is the position error,

which is defined as the difference between the

current and the desirable position. Since for safety

reasons we do not want the stand to rotate out of its

limits (-180

to 180

which corresponds to -30 to 30

in odometer units) we set the range of the position

error variable to be between -30 to 30 (in odometer

units). The linguistic variables for these inputs are:

negative big (NB), negative (N), zero (ZERO),

positive (P), positive big (PB) (Figure 7).

-80 -60 -40 -20 0 20 40 60 80

0.2

0.4

0.6

0.8

Roll angle (deg)

ZERO

-80 -60 -40 -20 0 20 40 60 80

0.2

0.4

0.6

0.8

Pitch angle (deg)

ZERO F

BB FB

-40 -30 -20 -10 0 10 20 30 40

0.2

0.4

0.6

0.8

Position Error

ZERO

NB PB

-6 -4 -2 0 2 4 6

0.2

0.4

0.6

0.8

Change of Position Error

ZERO

-30 -20 -10 0 10 20 30

0.2

0.4

0.6

0.8

Altitude (cm)

Figure 7: Membership functions for input variables.

The next input in the fuzzy controller is the

change of position error. While position error shows

how far the helicopter is from the desire position,

change of position error shows how fast the vehicle

is moving towards or away from the desired point.

This input is defined as the difference (in odometer

units) between the previous position error and the

current position error, and it is represented by the

linguistic variables: negative (N), zero (ZERO),

positive (P) (Figure 7).

The last input is the altitude error input. This

input represents the difference in cm between actual

and desired altitude by counting if the helicopter is

placed lower or higher than the desired position. The

linguistic variables for this input are: lower (L),

desired (D), higher (H) (Figure 7).

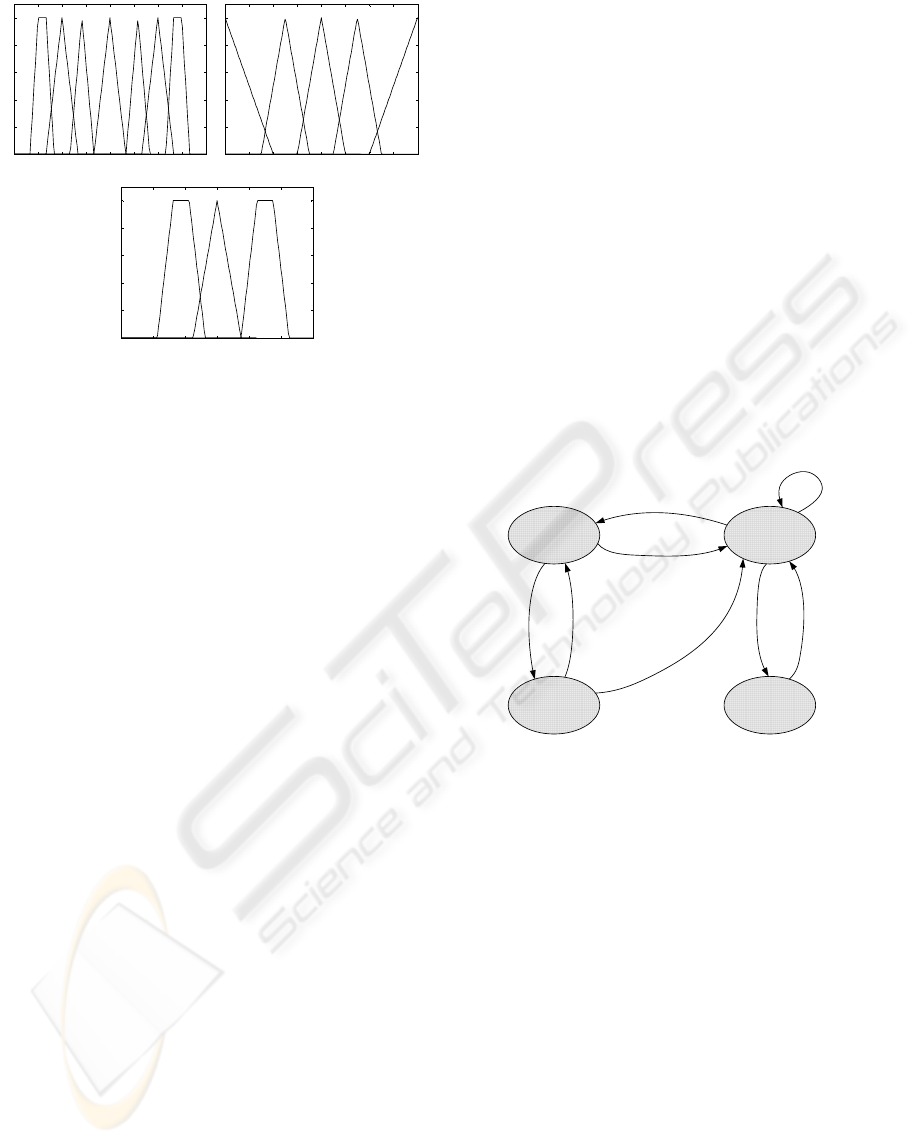
The outputs of the fuzzy controller are the

changes of roll and pitch angles (Aileron and

Elevator movements respectively) and Throttle

change. The membership functions of aileron,

elevator and throttle, are presented in Figure 8. The

linguistic variables for aileron are left big (LB), left

(L), left small (LS), zero (ZERO), right small (RS),

right (R) and right big (RB). The linguistic variables

for elevator are back big (BB), back (B), zero

(ZERO), front (

F) and front big (FB). Both aileron

and elevator output values are presented in control

signal units.

ALTITUDE CONTROL OF SMALL HELICOPTERS USING A PROTOTYPE TESTBED

-0.6 -0.45 -0.3 -0.15 0 0.15 0.3 0.45 0.6

0.2

0.4

0.6

0.8

Aileron

ZERO

-0.6 -0.45 -0.3 -0.15 0 0.15 0.3 0.45 0.6

0.2

0.4

0.6

0.8

Elevator

ZERO

-6 -4 -2 0 2 4 6

0.2

0.4

0.6

0.8

Throttle

ZERONP

Figure 8: Membership functions for output variables.

The linguistic variables for throttle change are

negative (N), zero (ZERO) and positive (P). The

values of throttle output are also presented in control

signal units. Negative output reduces throttle of the

helicopter while positive output increases it.

It should be noted that in order to simplify the

experimentation the yaw angle of the helicopter was

set to zero. This is due to the fact that the yaw angle

(tail movements) is usually stabilized in these

helicopters by a gyro mechanism.

3.2 Control Rules

The control objective in the experiments performed

was the stabilization of helicopter at a certain point

(defined by horizontal and vertical target

coordinates). The transition between the states of the

controller is presented in Figure 9, while in Figure

10 the pseudo-code that describes the control

scheme is shown. After take-off, the controller has

as a target to hover the helicopter. Then checks

actual horizontal position and drives the helicopter

to the desired one. The next step is checking of

actual altitude in order to drive the helicopter to the

desired one. After some iterations where the

helicopter hovers in the target point, the controller

lands it.

For the implementation of this scheme, three sets

(rule bases) of fuzzy IF-THEN rules were used. The

one was responsible for the control of the pitch

angle. The target was to keep the pitch angle always

close to zero as this is what needs to be done when

the helicopter hovers. This was achieved with simple

rules of the form: <IF Pitch is X THEN Elevator is

Y>, where X, Y represent the membership function of

pitch and elevator, respectively.

The second rule base contains rules of the form:

<IF Roll is A AND position error is B AND change

of position error is C THEN aileron is D>. These

rules lead the helicopter towards the desired point as

they tend to minimize the distance between the

helicopter’s horizontal position at each moment and

the desired one. This is a typical PD-like fuzzy

controller with one extra input: the roll angle.

The third rule base is responsible for handling

the throttle of the helicopter. The policy we follow

here is that the changes in the throttle of the

helicopter occur only when the helicopter is in stable

hovering attitude on the desired horizontal position

(roll and pitch angles are close to zero, change of

position error is close to zero) or when the altitude

becomes higher than a top safety limit. The rules of

this rule base have the form <IF Roll is A AND

position error is B AND change of position error is

C AND Altitude is D THEN throttle is E>.

TAKE-OFF

AND

LANDING

HOVERING

HORIZONTAL

TARGET

VERTICAL

TARGET

ATTITUDE

NOT STABLE

ATTITUDE

STABLE

TARGET

REACHED

TARGET

REACHED

TARGET

NOT REACHED

TAKE-OFF

LANDING

TARGET

NOT REACHED

Figure 9: Controller state transition.

If attitude is not stable

Stabilize helicopter to hovering

Else

If current horizontal position is not the

desired

Drive helicopter to the desired

horizontal position

Else

If Current Altitude is not the desired

Change throttle in order to reach

target altitude

Else

Hovering

End IF

End If

Figure 10: Pseudo code of the hovering controller.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

4 EXPERIMENTAL RESULTS

Experimental results for two test cases may be seen

in Figures 11 and 12. In these figures Roll and Pitch

values are measured in degrees, while Position

Error and Change of Position Error are measured in

odometer units (here, 1 odometer unit corresponds to

6 degrees) and Altitude is measured in centimetres.

Elevator, Aileron and Throttle values are measured

in control signals (values that PIC accepts as input

and automatically translates into servo signals). The

initial altitude of the helicopter (when the flying

stand is on the ground) is 10cm, since in this altitude

the infrared sensor is mounted to the stand.

0 100 200 300 400 500

-20

Roll

(deg)

0 100 200 300 400 500

-20

Pitch

(deg)

0 100 200 300 400 500

-20

Position

Error

0 100 200 300 400 500

-4

Change of

Pos Error

0 100 200 300 400 500

Altitude

(cm )

0 100 200 300 400 500

-0.5

0.5

Aileron

0 100 200 300 400 500

-0.5

0.5

Elevator

0 100 200 300 400 500

-4

Throttle

Iterations

Figure 11: Experimental results for test case 1.

In test case 1 (Figure 11) the ability of the

controller to perform autonomous take-off and keep

the helicopter in a hovering state, is evaluated. The

helicopter is placed on the desired horizontal

position by the human operator and then the

autopilot takes over with a target altitude of about 22

cm. As it can be seen in Figure 11, the controller

keeps roll and pitch angles close to zero and

gradually increases throttle in order to increase the

altitude and reach the target one. When the target

altitude is reached few oscillations around the target

horizontal position occur but the controller manages

to hold the helicopter in hovering in the desired

position. In the beginning, it is clear that position

error tends to be a small positive number, which

means that the helicopter always drifts to the left of

the desired position. This is explained by the

position of the test bed area which is close to the

walls of the building. Air flow from the main rotor

of the helicopter circles through the walls and return

as a disturbance to the helicopter. This air flow gives

a small drift to helicopter to the left. The developed

controller seems to recognize this disturbance and

make corrections in order to hold stable the

helicopter in the desired position.

0 50 100 150 200 250 300 350

-50

Roll

(deg)

0 50 100 150 200 250 300 350

-20

Pitch

(deg)

0 50 100 150 200 250 300 350

-20

Position

Error

0 50 100 150 200 250 300 350

-2

Change of

Pos Error

0 50 100 150 200 250 300 350

Altitude

(cm )

0 50 100 150 200 250 300 350

-0.5

0.5

Aileron

0 50 100 150 200 250 300 350

-0.5

0.5

Elevator

0 50 100 150 200 250 300 350

-4

Throttle

Iterations

Figure 12: Experimental results for test case 2.

In Figure 12 we present the results of test case 2.

In this test, the initial position of the helicopter is

different from the desired one and the controller

objective is to drive the helicopter to the desired

ALTITUDE CONTROL OF SMALL HELICOPTERS USING A PROTOTYPE TESTBED

position and then land it autonomously. The

helicopter is placed manually to a random position

and then the fuzzy autopilot gains control of the

helicopter. As one may see in the Position Error plot

of Figure 12, the helicopter moves manually from its

initial position to a random position. At time instant

50, the autopilot gains control of the vehicle. The

target of the autopilot is to move the helicopter to

the initial position and in 20 cm altitude. It is clear

that the autopilot drives the helicopter to the target

point by moving it to the desired horizontal position

at first and then by raising the altitude until the

targeted one has been reached. After a few iterations

that the target position has been reached, the

controller reduces the throttle and lands the

helicopter. Small oscillations occur while the

autopilot tries to keep the helicopter in stable

position. It is also clear, as in test case 1, that we

face the air disturbance that causes small drift in the

helicopter in this test case too.

5 CONCLUSIONS

In this paper we presented a fuzzy controller for

hovering and altitude control of a small-scale

helicopter. The controller was developed and tested

on a custom made laboratory experimental test bed,

where tests on unmanned helicopters can be

performed with safety. The test bed works indoors,

is independent of power supply and can be used for

continuous tests. The development of the controller

is done on a real helicopter and not in simulation, so

we can have direct and reliable results. The

experimental results show that this setup works well.

Experimental results from the evaluation of the

altitude fuzzy controller were presented.

Future work, involves development of other kinds

of controllers which will be tested and evaluated on

the test bed. This work will lead to a comparison of

controllers based on their efficiency and ability to

control successfully an unmanned helicopter.

ACKNOWLEDGEMENTS

This paper is part of the 03ED365 research project,

implemented within the framework of the

“Reinforcement Programme of Human Research

Manpower” (PENED) and co-financed by National

and Community Funds (75% from E.U.-European

Social Fund and 25% from the Greek Ministry of

Development-General Secretariat of Research and

Technology).

REFERENCES

Andrievsky, B., Peaucelle, D., and Fradkov, A., 2007.

Adaptive control of 3DOF motion for LAAS

helicopter benchmark: Design and experiments. In

Proceedings of the 2007 American Control

Conference, New York City, USA.

Dzul, A., Lozano, R., and Castillo, P., 2004. Adaptive

control for a radio-controlled helicopter in a vertical

flying stand. International Journal of Adaptive

Control and Signal Processing, 18:473-485.

Kim, H., and Shim, D., 2003. A flight control system for

aerial robots: algorithms and experiments. Control

Engineering Practice, 11:1389-1400.

Kim, N., Calise, A., Corban, J. E., and Prasad, J. V. R.,

2004. Adaptive output feedback for altitude control for

an unmanned helicopter using rotor RPM. In

Proceedings of AIAA Guidance, Navigation, and

Control Conference and Exhibit, Rhode Island, USA.

Kutay, A., Calise, A., Idan, M., and Hovakimyan, N.,

2005. Experimental results on adaptive output

feedback control using a laboratory model helicopter.

IEEE Transactions on Control Systems Technology,

13:196-202.

Mancini, A., Caponetti, F., Monteriu, A., Frontoni, E.,

Zingaretti, P., and Longhi, S., 2007. Safe flying for an

UAV helicopter. In Proceedings of the 15th

Mediterranean Conference on Control & Automation,

Athens, Greece.

Merz, T., Duranti, S., and Conte, G., 2006. Autonomous

landing of an unmanned helicopter based on vision

and inertial sensing. Experimental Robotics IX, pp.

343-352.

Sapiralli, S., Sukhatme, G., and Montgomery J., 2002. An

experimental study of the autonomous helicopter

landing problem. In Proceedings of the International

Symposium on Experimental Robotics, Italy.

Shin, J., Nonami, K., Fujiwara, D., and Hazawa, K., 2005.

Model-based optimal attitude and positioning control

of small-scale unmanned helicopter. Robotica, 23:51-63.

Spanoudakis, P., Doitsidis, L., Tsourveloudis, N., and

Valavanis, K., 2003. The market for VTOL UAVs.

Unmanned Systems Magazine, Sept/Oct, pp. 14-18.

Tanaka, K., Ohtake, H., and Wang, H., 2004. A practical

design approach to stabilization of a 3-DOF RC

helicopter. IEEE Transactions on Control Systems

Technology, 12:315-325.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics