PERCEPTUAL MOTOR CONTROL MODEL BASED ON OUTPUT

FEEDBACK ADAPTIVE CONTROL THEORY

Hirofumi Ohtsuka, Koki Shibasato

Department of Electronic Control, Kumamoto National College of Technology

2659-2 Suya, Koshi, Kumamoto, 861-1102, Japan

Shigeyasu Kawaji

Graduate School of Science and Technology, Kumamoto University

2-39-1 Kurokami, Kumamoto, 860-8555, Japan

Keywords:

Human-machine system, adaptive control, output feedback, perceptual motor system, cerebellum.

Abstract:

In this paper, a Perceptual Motor Control Model(PMCM) based on output feedback adaptive control theory is

considered from the viewpoint of voluntary movement such as hand-tracking control. We give an account of

the PMCM structure using together with both of the output feedback controller designed by using an almost

strict positive real characteristics for the controlled plant and the Smith predictor for plant with pure time

delay. In the proposed method, the attractive structural similarity exists between the cerebrum-cerebellum

neuro-motor signal feedback loop and the adaptive controller - compensators local minor feedback loop. The

proposed perceptual motor control model is evaluated through the comparison of between the experiment and

the simulation of for handling 1-link mechanism in order to track an indicator.

1 INTRODUCTION

The construction of collaborative human-machine

system is being recognized as an important technol-

ogy from the viewpoint of human centered assist-

ing system development (Takahashi and Ikeura, 2006;

Yamada and Utsugi, 2006). While such assisting sys-

tems aim at partial replacement of control task or

an ampliﬁcation of control power, those have insuf-

ﬁciency in order to achieve the accurate maneuver-

ing, where human performs as a main controller in

the human-machine system. For the purpose of im-

provement of the maneuvering performance and the

response of human-machine system, authors have de-

veloped a new compensator named as ”collaborater”,

which can support the collaborative work of human

and machine (Ohtsuka et al., 2007). The model of hu-

man response behavior is required to design the col-

laborater and the collaborative assisting system, but

it has been difﬁcult to construct an accurate model

of human perceptual motor control system (e.g., limb

and muscle). Kleinman et al. applied optimal con-

trol theory to develop a model of human behavior in

manual tracking tasks (Kleinman et al., 1970). Their

model contains time delay, a representation of neuro-

motor dynamics, and controller remnant as limita-

tions. Recently, Furuta considers that the analysis of

human control action is one of fundamental problems

in the study of human adaptive mechatronics (Furuta

et al., 2004). From such a viewpoint, in the authors’

previous study, Delayed Feed-Forward (DFF) Model

has been used for describing human’s hand-tracking

motion with visual information (Ishida and Sawada,

2003). The DFF model can realize the characteristics

that the limb motion, with prediction of target posi-

tion, makes the predicted value to minimize the tran-

sient error in the considering frequency range. How-

ever, for the non-cyclical target value and/or the con-

trolled machine output, it has been resulted in that

the DFF model has an insufﬁcient reliance because

of the shortage of consideration through the experi-

mental study.

In this paper, for the upper limb motion in the

hand-tracking control, a new Perceptual Motor Con-

trol Model (PMCM) is considered. Namely, the visual

feedback controller is modeled as the output feed-

back type adaptive controller stabilizing the closed

loop system based on an Almost Strict Positive Real

(ASPR) characteristic of the controlled system. The

Parallel Feed-forward Compensator (PFC) has been

introduced in order to make an ASPR augmented sys-

tem (Iwai et al., 1993). And, Miall et al. have

115

Ohtsuka H., Shibasato K. and Kawaji S. (2008).

A PERCEPTUAL MOTOR CONTROL MODEL BASED ON OUTPUT FEEDBACK ADAPTIVE CONTROL THEORY.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 115-120

DOI: 10.5220/0001494301150120

 SciTePress

proposed a human’s brain model by introduction of

Smith Predictor (as forward internal model) in order

to predict the consequences of actions and to over-

come pure time delays of neuro-motor signal trans-

mission associated with feedback control (Miall et al.,

1993). So, taking into account of those approaches,

both PFC and Smith Predictor are located into the

minor feedback loop for the output feedback adap-

tive controller. So, the PMCM has similar structure

to the cerebrum-cerebellum neuro-motor signal feed-

back loop. The effectiveness of the proposed PMCM

is discussed through the comparison between the ex-

periment and simulation results.

2 OUTPUT FEEDBACK TYPE

ADAPTIVE CONTROL SYSTEM

In this section, as a preparation for discussion about

the PMCM of human, we brieﬂy outline an output

feedback adaptive control method, where the con-

troller is designed to realize the plant output converg-

ing to reference signal. Let us consider the following

SISO plant:

˙x(t) = Ax(t) + bu(t)

y(t) = c

x(t)

(1)

where x is the nth order state vector, u and y are scalar

input and output, respectively. A, b and c are unknown

matrix and vectors with appropriate dimensions. The

transfer function form of the plant Eq.(1) is expressed

G(s) = c

(sI − A)

−1

b + d =

N(s)

D(s)

N(s) = b

+ b

m−1

+ · · · + b

s + b

D(s) = s

+ a

n−1

+ · · · + a

s + a

(2)

Now, we make the following assumption.

Assumption 1. The Plant Eq.(1) or Eq.(2) is

ASPR(Almost Strictly Positive real).

From this assumption, there exists a constant gain k

such that the transfer function

(s) = (1 + k

G(s))

−1

G(s) (3)

is SPR(Strictly Positive Real). Sufﬁcient condition

for Assumption 1 can obtained, such that (1) N(s) is

Hurwitz polynomial, (2) γ = n− m ≤ 1, and (3) b

> 0

(Kaufman et al., 1998). Under the Assumption 1, the

following adaptive algorithm:

u(t) = k(t)e(t) (4)

k(t) = ge(t)

(5)

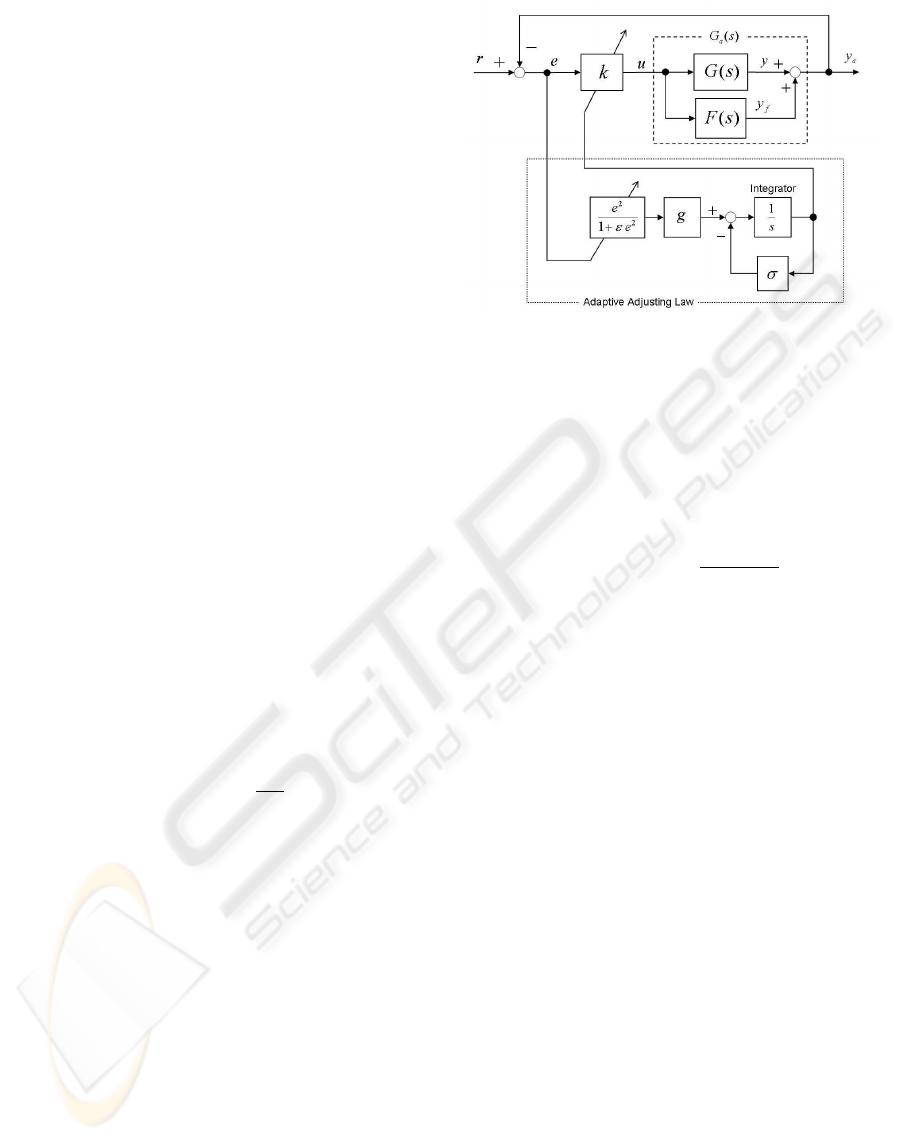
Figure 1: Adaptive Control System with PFC.

generates the control of the plant Eq.(1), where e(t) =

r(t) − y(t) and g is positive constant. And, it can

achieve the output error e(t) convergence to zero.

Furthermore, against to the input disturbance and to

the un-modeled dynamics of the plant, the following

modiﬁed adaptive adjusting law

k(t) = −σk(t) + g

e(t)

1 + εe(t)

, (6)

can be utilized in order to maintain that the all sig-

nals in the closed loop system become uniformly ulti-

mate bounded (UUB), where σ and ε are given as suf-

ﬁciently small positive constants (Iwai et al., 1993).

However, Assumption 1 is not satisﬁed by most

practical systems with large relative degree γ > 1. To

overcome this problem, as shown in Fig.1, dynamic

compensator F(s) is introduced to construct the aug-

mented ASPR plant G

(s) = G(s) + F(s) satisfying

the above-stated sufﬁcient condition. Thus, the out-

put feedback adaptive control law can be applied to

the augmented plant G

(s) and maintain the stability

of closed loop system. So, F(s), located in parallel

path for the plant, is called as parallel feedforward

compensator (PFC) (Kaufman et al., 1998).

3 PERCEPTUAL MOTOR

CONTROL MODEL

In the brain science research area, the cerebellum has

attracted the attention of theorists and modelers, and

the need for a unifying theory for the role of the cere-

bellum in motor control has been recognized for many

years (Miall et al., 1993; Ito, 1970; Wolpert et al.,

1998; Kleinman et al., 1970). Specially, based on

data from the control of the primate arm in visu-

ally guided tracking tasks (Fig.2), Miall et al. have

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

116

Figure 2: Human Body Dynamics.

Table 1: Parameters and Variables.

Notation Parameters and Variables

r(t) position of the target

y(t) position of the hand

v(t) command signal from the brain

dead time in the nervous system from

the retina to the brain

dead time in the nervous system from

the brain to the muscle

time constant of the brain

time constant of the muscle dynamics

suggested that the cerebellum acts as a Smith Pre-

dictor, which is based on internal representation of

controlled object suffering with long and unavoidable

feedback delays. Ito et al. also suggested that there

exists the cerebrum-cerebellum neuro-motor signal

feedback loop (Fig.3) and the cerebellum may form

the internal model, based on physiological and clin-

ical evidence (Ito, 1970). There are two varieties of

internal model, i.e., forward model and inverse model

(Wolpert et al., 1998). Forward models capture the

forward or causal relationship between inputs to the

system, such as the arm, and the outputs. The Smith

predictor can be regarded as a kind of forward model.

While the problem of pure time delay can be over-

come by Smith predictor, the performance of visual

feedback control is mainly affected by the setting of

output feedback gain. However, conventional most

of neuro motor models have ﬁxed the feedback gain

as constant. On the other hand, the adaptive control

methods, based on the ability of animal to adapt itself

to changes in its surroundings, have been developed.

Taking into account of both the concept of adap-

tive control method and the brain science researchers’

suggestions, let us construct a new perceptual motor

Figure 3: Cerebrum & Cerebellum (Ito, 1970).

control model as shown in Fig.4 for the control prob-

lem as shown in Fig.2, in which a human operator

controls the machine to follow the target. Here, the

time delay of nervous system transmission is success-

fully compensated by Smith predictor:

(s) − G

(s)e

−(δ+ζ)s

(7)

where G

(s) = G

(s)/(τ

s + 1).

Then, the controlled system from a side of the out-

put feedback adaptive controller becomes a series of

three elements. Namely, it consists a ﬁrst lag ele-

ment with time constant τ

which is involved in brain

dynamics, a ﬁrst lag element with time constant τ

which is involved in muscle dynamics, and a con-

trolled machine dynamics G

(s). In order to con-

struct a stable output feedback adaptive control sys-

tem, the ASPR compensation must be implemented

for G(s) = G

(s)/(τ

s + 1). So, suppose that the fol-

lowing assumption holds.

Assumption 2. G(s) satisﬁes that

(1) G(s) is minimum phase system.

(2) the relative degree γ is larger than 2.

(3) the nominal value of the leading coefﬁcient b

G(s) is known.

Then, according to one of practical PFC design

method (Iwai et al., 1994), PFC:F(s) as shown in

Fig.5 can construct the augmented plant G(s) + F(s)

which satisﬁes the above-mentioned sufﬁcient condi-

tion for Assumption 1. Here, δ is sufﬁciently small

positive constant, γ is a relative degree of G(s), α

are

positive constants and β

are coefﬁcients of the Hur-

witz polynomial:

R(s) = β

γ−1

+ · · · + β

s + β

, (8)

where β

is a leading coefﬁcient of G(s). Both the

Smith predictor and PFC can be located into the mi-

A PERCEPTUAL MOTOR CONTROL MODEL BASED ON OUTPUT FEEDBACK ADAPTIVE CONTROL THEORY

117

Figure 4: Perceptual Motor Control Model.

Figure 5: Ladder Network Type PFC (Iwai et al., 1994)

nor feedback loop for the output feedback gain k ad-

justed by the adaptive algorithm Eq.(6) using e

(t)

instead of e(t). So, it ease to recognize that such mi-

nor feedback structure is very similar to the cerebrum-

cerebellum neuro-motor signal feedback loop model

in Fig.3. Thus, we can imagine that the Smith predic-

tor and PFC perform the role of cerebellum.

4 EVALUATION OF PMCM

Fig.6 shows the experimental equipment for the vir-

tually guided tracking task. An indicator shows the

target position, which is driven by AC motor 1, and

the operator controls a handle to follow the indicator.

AC motor 2 is assembled in order to generate the as-

Figure 6: Experimental Equipment.

sisting torque for the operator, while it performs as a

load inertia for human in this situation.

Mechanical System. From the experimental results

of automatic positioning control, the transfer function

of the one-link arm mechanism involving AC motor 2

was estimated as follows

(s) =

4213

s(s + 1)

(9)

Human Dynamics Model. Through the experimental

results, the parameters of human dynamics model are

estimated such that δ +ζ = 0.13[s], τ

= τ

= 0.03[s],

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

118

0 0.2 0.4 0.6 0.8 1 1.2

-5

Time [s]

Angle [degree]

Figure 7: Experimental Results.

0 0.2 0.4 0.6 0.8 1 1.2 1.4

-1

-0.5

0.5

Time[s]

Torque [Nm]

Figure 8: Input Torque (Experiment).

respectively (Saito and Nagasaki, 2002). In this case,

the controlled system from a side of the output feed-

back controller, which is the above-mentioned series

of three elements is given as follow.

G(s) =

4213

s(s + 1)(0.03s + 1)

(10)

PFC. Because G

(s) has a relative order as 3 and

minimum phase characteristics, for the simulation,

PFC is constructed as follows:

F(s) =

(τ

s + 1)(s + α)

(τ

s + 1)(s + α)

, (11)

where design parameters are given as f

= 350, f

6, α = 0.5.

Results of Experiment and Simulation. Experi-

mental results for the target position r(t) = 30 [de-

gree] are shown as Fig.7 and Fig.8. And, Fig.9 and

Fig.10 also shows the simulation results for the vari-

ance of design parameter g in Eq.(6). In the sim-

ulation, the other parameters in Eq.(6) are given as

0 0.2 0.4 0.6 0.8 1 1.2 1.4

-5

Time [s]

Angle [degree]

g=0.006

g=0.009

g=0.012

g=0.02

Figure 9: Simulation Results.

0 0.2 0.4 0.6 0.8 1 1.2 1.4

-1

-0.5

0.5

Time [s]

Input Torque [Nm]

g=0.006

g=0.009

g=0.012

g=0.02

Figure 10: Input Torque (Simulation).

k(0) = 0, σ = 0.1 and ε = 0.01. Although there exists

some ﬂuctuation in the experimental results obtained

for three testors, we can recognize that the both re-

sponses are very similar. Because, by comparing be-

tween Fig.7 and Fig.9, the overshoots are almost same

level and the damping ratio and the values of peak

time are close resemblance. Furthermore, by com-

parison of Fig.8 and Fig.10, both signal wave forms

also show a close similarity. So, we can note that the

proposed model can maintain its good performance.

Furthermore, we can set up a hypothesis such that

the ﬂuctuation in the response occurring every exper-

iment can be interpreted as the ﬂuctuation of PMCM

parameters.

5 CONCLUSIONS

From the point aimed at the minor feedback loop in

the brain, i.e., the nervous network between the cere-

brum and the cerebellum performing minor feedback

A PERCEPTUAL MOTOR CONTROL MODEL BASED ON OUTPUT FEEDBACK ADAPTIVE CONTROL THEORY

119

loop element, and a hypothesis for cerebellum gen-

erating a forward model of motor apparatus dynam-

ics, a perceptual motor control model has been dis-

cussed. The proposed method is based on output feed

back type adaptive control using ASPR characteristics

of the controlled plant, which accompany with PFC.

In the nervous network, there necessarily exists dead

time (pure time delay) of signal transmission between

cortex and lower apparatus. To overcome the inﬂu-

ence of the feedback of the sensed signal involving

time delay, the Smith predictor method is introduced.

From the viewpoint of the mutual connection be-

tween the cerebrum and the cerebellum, we showed

that the PFC and Smith predictor perform as cere-

bellum generating a forward model for the controlled

machine and human’s motor apparatus, and the adap-

tive controller performs as cerebrum adjusting the vi-

sual feedback control signal. The effectiveness of the

proposed model was examined through the compar-

ison between of experimental results and simulation

results for one-link arm positioning control problem.

And, it was conﬁrmed that the proposed model can

represent the manual control response with sufﬁcient

accuracy.

REFERENCES

Furuta, K., Iwase, M., and Hatakeyama, S. (2004).

Analysing saturating actuator in human-machine sys-

tem from view of human adaptive mechatronics. In

Proceedings of REDISCOVER 2004, Vol.1, (3-1)–(3-

9).

Ishida, F. and Sawada, Y. (2003). Quantitative studies of

phase lead phenomena in human perceptro-motor con-

trol system. In Trans. of SICE, Vol.39, No.1, 59-66.

Ito, M. (1970). Neurophysiological aspects of the cerebel-

lar motor control system. In International Journal of

Neurology, Vol. 7, 162-176.

Iwai, Z., Mizumoto, I., and Deng, M. (1994). A par-

allel feedforward compensator virtually realizing al-

most strictly positive real plant. In Proc. of 33

IEEE

CDC, 2827-2832.

Iwai, Z., Mizumoto, I., and Ohtsuka, H. (1993). Robust

and simple adaptive control system design. In Inter-

national Journal of Adaptive Control and Signal Pro-

cessing, Vol.7, 163-181.

Kaufman, H., Bar-Kana, I., and Sobel, K. (1998). Direct

Adaptive Control Algorithms Theory and Application.

Springer-Verlag, New York, 2nd edition.

Kleinman, D. L., Baron, S., and Levison, W. H. (1970). An

optimal control model of human response part i: The-

ory and validation. In Automatica, Vol.6, 357-369.

Miall, R. C. ., Weier, D. J., Wolpert, D. M., and Stein, J. F.

(1993). Is the cerebellum a smith predictor ? In Jour-

nal of Motor Behavior, Vol.25, No.3, 203-216.

Ohtsuka, H., Shibasato, K., and Kawaji, S. (2007). Collab-

orative control of human-machine system by collabo-

rater. In Trans. of The Japan Society of Mechanical

Engineers, Series C, Vol.73, No.733, 2576-2582.

Saito, H. and Nagasaki, H. (2002). Clinical Kinesiology.

Ishiyaku Publishers, Inc., 3rd edition.

Takahashi, T. and Ikeura, R. (2006). Development of human

support system. In Journal of the Society of Instru-

ment and Control Engineers,Vol.45, No.5, 387-388.

Wolpert, D. M., Miall, R. C., and Kawato, M. (1998). Inter-

nal models in the cerebellum. In Trends in Cognitive

Sciences, Vol.2, No.9, 338-347.

Yamada, Y. and Utsugi, A. (2006). Human intention infer-

ence techniques in human machine systems and their

robotic applications. In Journal of the Society of In-

strument and Control Engineering, Vol.45, No.6, 407-

412.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

120