BEHAVIOR BASED DEPENDABILITY ESTIMATION
Estimating the Dependability of Autonomous Mobile Systems using Predictive Filter
Jan R¨udiger, Achim Wagner and Essam Badreddin
Automation Laboratory, University of Mannheim, B6, 23-29, Building B, EG, 68131 Mannheim, Germany
Keywords:
Fault-tolerant systems, Autonomous systems, Behavioral systems.
Abstract:
Dependability is getting a more important non-functional property of a system. Measuring and predicting the
dependability is especially important for autonomous or semi-autonomous and safety-critical systems. Since,
at least for (semi-) autonomous systems, those systems are usually described by their behavior, a definition for
dependability based on the behavior of the system is evident. In this paper the behavioral based definition of
dependability was used together with a particle filter to estimate the dependability of an autonomous mobile
system.
1 INTRODUCTION
Non-functional properties reflect the overall quality
of a system. Beside performance the dependability is
getting a more important non-functional requirement
of a system. The general, qualitative, definitions for
dependability used in the literature so far are (in his-
torical order):
Military Standard. (Department of Defense,
1970) A measure of the degree to which an
item is operable and capable of performing its
required function at any (random) time during
a specified mission profile, given item avail-
ability at the start of the mission.
Carter. (Carter, 1982) A system is depend-
able if it is trustworthy enough that reliance
can be placed on the service it delivers.
Laprie. (Laprie, 1992) Dependability is that
property of a computing system which allows
reliance to be justifiably placed on the service
it delivers.
Badreddin. (Badreddin, 1999) Dependability
in general is the capability of a system to suc-
cessfully and safely fulfill its mission.
Dubrova. (Dubrova, 2006) Dependability is
the ability of a system to deliver its intended
level of service to its users.
All definitions have in common that they define de-
pendability on the service a system delivers and the
trust that can be placed on that service. The service a
system delivers, however, is the behavior as it is per-
ceived by the user, which in our case will be called
the mission of the system. They also have in com-
mon that they don’t define a system independent way
of how the measure or evaluate the dependability of
a system. Comparing the dependability of different
systems, even if a dependability measure for specific
systems exists (see (Wilson et al., 2002; Kanoun et al.,
2002; Brown et al., 2002; Rus et al., 2002; Cukier and
Smidts, 2002; Mukherjee and Siewiorek, 1997; Arlat
et al., 1990)), is almost impossible.
According to (Avizienis et al., 2004b; Avizienis et al.,
2004a; Randell, 2000) dependability is understood as
an integrated concept that further consists of different
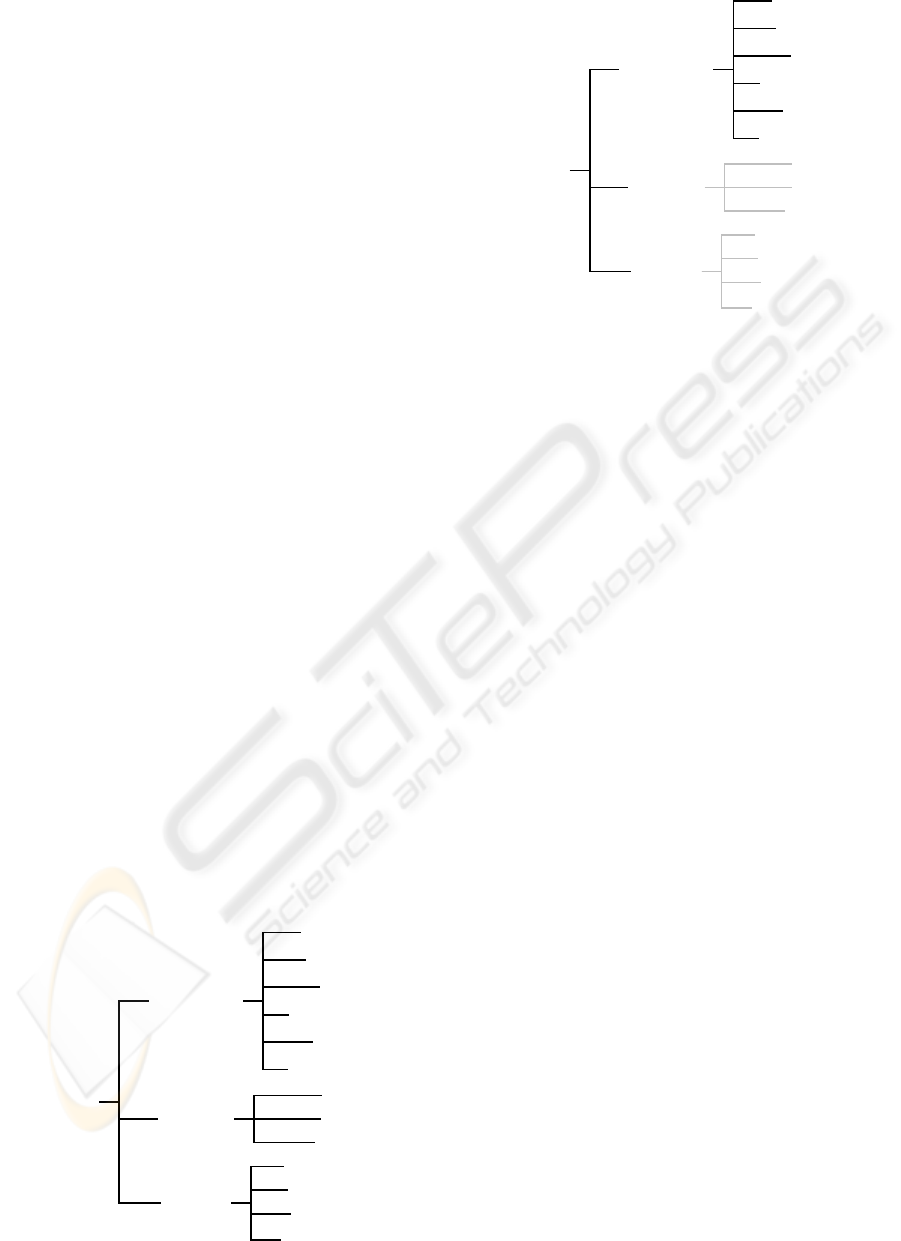
attributes, threads and means (see Fig. 1). This set
of attributes is, however, application specific and thus
not fix. In (Candea, 2003) and (Dewsburyet al., 2003)
different sets of attributes for evaluating the depend-
ability were proposed. In (R¨udiger et al., 2007b) a
reduction of the dependability tree was proposed for
the application of autonomous mobile systems. The
reduced dependability tree is presented in Fig. 2.
This paper is outlined as follows: In Section 2 a
short introduction to the framework of dynamic sys-
tems described by their behavior is presented leading
to a definion for a system together with a mission, de-
fined in this framework. The section concludes with a
definition for a measure for the dependability of this
system. Section 2.5 describes different methods of
how to apply this definition to actually measure the
137
Rüdiger J., Wagner A. and Badreddin E. (2008).
BEHAVIOR BASED DEPENDABILITY ESTIMATION - Estimating the Dependability of Autonomous Mobile Systems using Predictive Filter.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 137-142
DOI: 10.5220/0001495801370142
Copyright
c
 SciTePress

dependability. The results of a simulation using par-
ticle filter are then presented in Section 4. The paper
ends with a discussion of the results in Section 5.
2 BEHAVIOR BASED
DEPENDABILITY DEFINITION
2.1 System Definition
In the framework of Willems (see (Willems, 1991))
a system is defined in an universum U. Elements of
U are called outcomes of the system. A mathemati-
cal model of a system from a behavioral or black-box
point of view claims that certain outcomes are possi-
ble, while others are not. The model thus defines a
specific subset B ⊂ U. This subset is called the be-
havior of the system.
A (deterministic) mathematical model of a system is
then defined as:
Definition 1. A mathematical model is a pair (U, B)
with the universum U - its elements are called out-
comes - and B the behavior.
A dynamical system is a set of trajectories describ-
ing the behavior of the system during the time instants
of interest in W.
In contrast to the state space representation, like ˙x =
f ◦x, Willems (see (Willems, 1991)) defines a dynam-
ical system as:
Definition 2. A dynamical system
∑
is a triple
∑
=
(T, W, B) with T ⊆ R the time axis, W the signal
space, and B ⊆ W
T
the behavior.
Furthermore an autonomous system is defined as:
Definition 3. (Autonomous System) Let Σ =
(T, W, B), T = Z or R, be a time-invariantdynamical
Dependability
Attributes
Availability
Reliability
Safety
Confidentiality
Integrity
Maintainability
Threats
Faults
Errors
Failures
Means
Fault Prevention
Fault Tolerance
Fault Removal
Fault Forecasting
Figure 1: The dependability tree.
Dependability
Attributes
Availability
Reliability
Safety
Confidentiality
Integrity
Maintainability
Threats
Faults
Errors
Failures
Means
Fault Prevention
Fault Tolerance
Fault Removal
Fault Forecasting
Figure 2: Reduced dependability tree for autonomous mo-
bile systems.
system. Σ is said to be autonomous if
n
w
1
, w
2
∈ B and w
1(t)
= w
2(t)
for t < 0
o
⇒ {w
1
= w
2
}
The definition of an autonomous systems states
that the future behavior of the system is completely
defined by its past trajectory.
This aspect is an important assumption for modeling
the system later.
2.2 Behavior and Mission of
Autonomous System
To accomplish its task an autonomous system is usu-
allay given a set of behaviors. In (R¨udiger et al.,
2007a) the behavior set of the system was defined as:
Definition 4. (Behavior) Let Σ = (T, W, B) be a
time-invariant dynamical system then B ⊆ W
T
is
called the set of basic behaviors w
i
(t) : T → W, i =
1...n and B the set of fused behaviors.
Likewise the mission of the system was defined
as:
Definition 5. (Mission) Let Σ = (T, W, B) be a time-
invariant dynamical system. We say the mission w
m
of this system is the map w
m
: T → W with w
m
∈ B.
The mission, as defined in (R¨udiger et al., 2007a),
is thus just a special trajectory or behavior in B. Hav-
ing the system together with a mission mathemati-
cally defined is important for a definition of depend-
ability.
2.3 Safe Area S
Before presenting a definition for dependability, at
least the definition for the attribute safety in a behav-
ioral context is needed.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
138

BS
w
Figure 3: Safety: The system trajectory w leaves the set of
admissible trajectories B but is still considered to be safe
since it remains inside S
While the other attributes of dependability, like avail-
ability, reliability etc., will only be indirectly included
in the dependability definition (see Section 2.4 be-
low), the attribute safety, since it is also included in
the dependability definitions seen in Section 1, is di-
rectly included in the definition (see (R¨udiger et al.,
2007a) for a definition of the remaining attributes in a
behavioral context).
From a reliability point of view, all failures are equal.
In case of safety, those failures are further divided
into fail-safe and fail-unsafe ones. Safety is reliabil-
ity with respect to failures that may cause catastrophic
consequences. Therefore safety is unformaly defined
as (see e.g. (Dubrova, 2006)):
Safety S(t) of a system is the probability that
the system will either perform its function cor-
rectly or will discontinue its operation in a
fail-safe manner.
For the formal definition of safety an area S was in-
troduced in (R¨udiger et al., 2007a) and further dis-
cussed in (R¨udiger et al., 2007b), which leads to
catastrophic consequences when left. This safety
area, however, must not be fully contained in the sta-
bility region of the system, but S is defined to be
around B (B ⊂ S). This margin is, like B, highly
system specific, but can be set equal to B for a re-
strictive system.
Definition 6. Let Σ = (T, W, B), T = Z or R, be a
time-invariant dynamical system with a safe area S ⊇
B. The system is said to be safe if for all t ∈ T the
system state w(t) ∈ S.
The definition is illustrated in Fig. 3. Leaving
the safe area S does not necessary render the system
un-operable for the rest of the mission. The above
definition of safety permits that the systems trajectory
returns to B thus making the system fully operable
again. This could be achieved be reconfiguration etc.
2.4 Dependability Definition
In (R¨udiger et al., 2007a) the dependability of a sys-
tem was defined as:
Definition 7. A time-invariant dynamical system Σ =
(T, W, B) with the behaviors B and a mission w
m
∈
B is said to be (gradually) dependable in the period
T ∈ T if, for all t ∈ T, the mission w
m
can be (gradu-
ally) accomplished.
To actually measure the dependability of a given
system, this definition needs, however, to be further
sophisticated. The main idea behind this definition is
to look at the dependability as the difference between
the mission trajectory w
m
and the system trajectory
w, which is the evolution of the system state. This,
together with the distance to the safety area S will be
the main idea of a measure for the dependability.
After the system Σ has completed its mission the de-
pendability D of this system with this mission w
m
can
be defined to as:
D
m
= 1−
1
t
∗
Z
t
∗
0
d(τ)dτ (1)
for the continuous case and for the non-continuous
case
D
m
= 1−
1
t
∗
t
∗
∑
0
d(τ). (2)
Where t
∗
is an appropriate normalizing faktor and
d is an appropriate measure of the difference between
the mission trajectory w
m
and the system trajectory w
and as such a combination of different distance mea-
surements. Those distance measurements will be dis-
cussed in the following.
More important than knowing the dependability
of a system after the completion of the mission is to
know the dependability during the mission. For this
the equation 1 and 2 is split up into a past and a future
part. With this the dependability can be computed to
be
D(t) = 1−





1
t
∗
Z
t
0
d(τ)dτ
| {z }
Past
+
1
t
∗
+ δ
Z
t+δ
t
d(τ)dτ
| {z }
Future





(3)
in the continuous case and for the non-continuous
case
D(t) = 1 −






1
t
t
∑
0
d(τ)
| {z }
Past
+
1
t
m
− t
t
m
∑
t+ε
d(τ)
| {z }
Future






(4)
BEHAVIOR BASED DEPENDABILITY ESTIMATION - Estimating the Dependability of Autonomous Mobile Systems
using Predictive Filter
139

Computing the d
i
(t) is, of course, system and ap-
plication specific. For the simulation only the distance
between the mission trajectory and the system tra-
jectory (d
m
(t)) and the relative distance between the
system trajectory and the safe area d
S
(t) were used,
since these both will be used in most of the depend-
ability measures.
The distance between the mission trajectory and the
system trajectory was chosen to be the minimum eu-
clidian distance between system state and the mission
trajectory.
d
m
(t) = 1 − e
−a∗

w(t)−w
m
(t)
w
m
(t)

2
(5)
The distance measure for safety d
S
(t) was chosen to
be a reliable measure even when the mission trajec-
tory w
m
itself is close to the safe area S. The d
S
is
defined as follows:
d
S
(t) = 1− e

min|S −w
m
(t)|
min|S −w(t)|

2
(6)
2.5 Measuring the Dependability
For computing the dependability of a system the ac-
tual state of the system and for adequate time horizon
the future states must be available with sufficient ac-
curacy. To achieve this different techniques are found
throughout the literature, among them:
• Using a model of the system and its environment
or
• probabilistic approaches like
– Kalman Filter or
– Particle Filter
If for the accomplishment of the mission a set of basic
behaviors B rather than only one behavior is available,
the minimum d of those behaviors needs to be taken
and the future part of dependability thus computes to:
Z
t
m
t+ε
min(d(t))
2
t
m
dt
| {z }
Future
(7)
If the System is further divided into sub-systems, the
different measures of those sub-systems needs also to
be joined according to the topology of the system.
3 DEPENDABILITY
MONITORING AS RECURSIVE
STATE ESTIMATION
The formulation of dependability presented above re-
quires estimating the state of the autonomous mobile
0 0.5 1 1.5 2 2.5
−1.5
−1
−0.5
0
0.5
1
1.5
X−Distance
Y−Distance
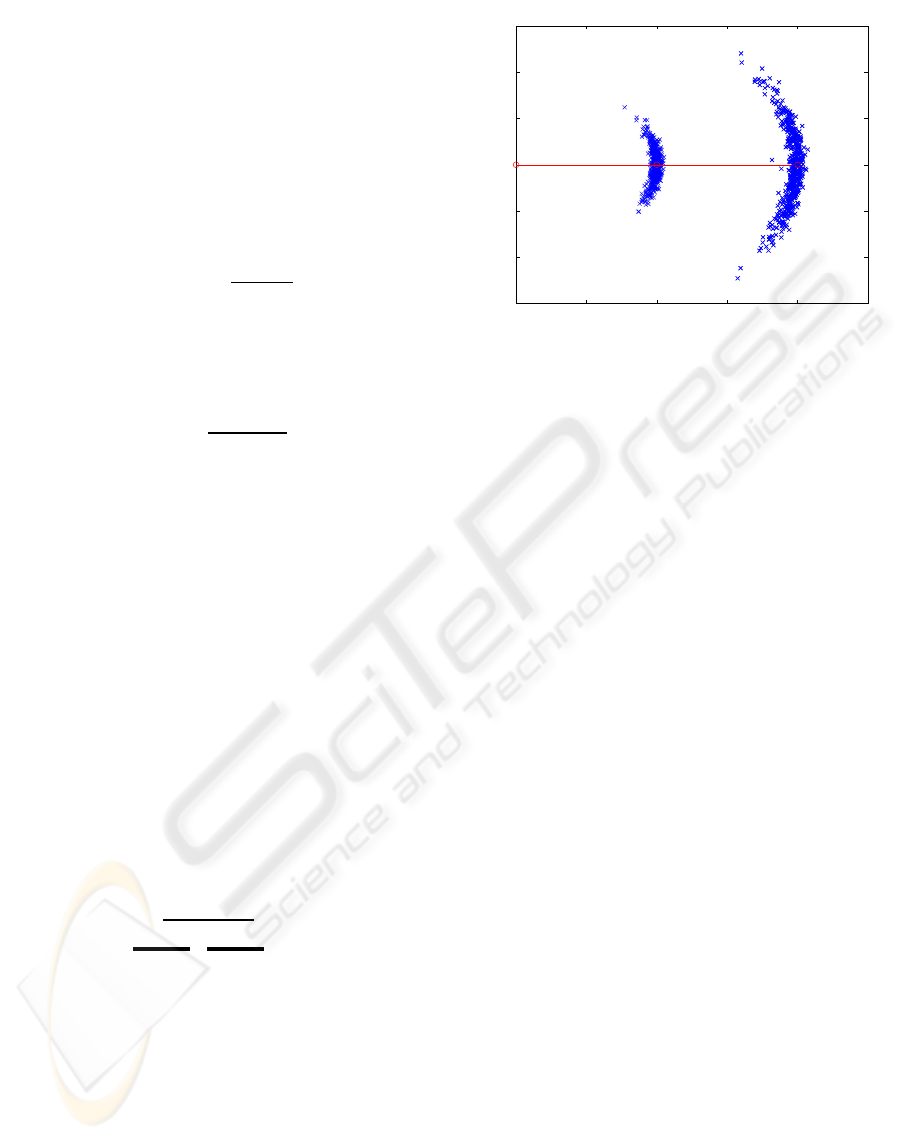
Figure 4: Prediction model of the robot for a translatory
movement of 1m and 2m used to predict the dependability
of the autonomous mobile system
system and the environment as it changes over time.
This information must then be compared to the mis-
sion trajectory w
m
to compute the dependability of the
system.
3.1 Model based State Estimation
Using the mathematical model to compute the de-
pendability of the system is the simplest way. This
method, however, can only insufficient deal with
changes in the system, which could happen due to
system degeneration etc., or changes in the environ-
ment. Furthermore mathematical models usually fo-
cus on a specific aspect of the system and as thus
aren’t adequate for computing the dependability. A
more sophisticated model of the robot and the envi-
ronment could compensate this disadvantage with the
cost of higher computation time.
3.2 Particle Filter based State
Estimation
Since Kalman Filter restricts the state transition and
the observation model to be linear functions of the
system state, particle Filter are used here to track the
state of the autonomous mobile system.
To be able to estimate the dependability with a par-
ticle filter, the system is modeled as Markovian, non
linear, non-Gaussian. A Sample Importance Resam-
pling Filter (SIR) (see e.g. (Arulampalam et al.,
2002),(Chen, 2003)) was then used in a simulation de-
scribed in the following section to estimate the system
state.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
140

ω
1
ω
2
ω
3
rr
Figure 5: Drawing of the robot used in the simulation.
Wheel ω
1
and ω
2
are two independently driven and mea-
sured conventional wheels. Wheel ω
3
is an undriven and
unmeasured castor wheel.
4 SIMULATION RESULTS
The robot in the simulation has two degree of free-
dom (DOF) as shown in Fig. 5. For evaluating the
dependability of this robot the state (pose)
x(t) =


x
y
φ


(8)
was estimated using a particle filter. The kinematic
model of the robot presented in Eq. 9 was used to
obtain the prediction model for the movement of the
robot.


x
k
y
k
φ
k


=


x
k−1
+ δ
s
cos(φ
k−1
)
y
k−1
+ δ
s
sin(φ
k−1
)
φ
k−1
+ δ
φ


(9)
In this equation δ
s
and δ
φ
where computed using the
movement of the wheels ω
1
and ω
2
. A Gaussian noise
modell is applied separately to each of the two types
of motion because they are assumed to be indepen-
dent. The resulting prediction model can be seen in
Fig. 4 for a translatory movement of 1m and 2m.
The observation model used in the simulation is
shown in the following equation.
y
k
=

ω
1
ω
2

=

δ
X
− rδ
φ
δ
Y
+ rδ
φ

Where r isthe distance between the center of the robot
and the contact point of the wheels (see Fig. 5) and
δ
X
, δ
Y
are the motion of the robot in X and Y direc-
tion according to the robot coordinate system.
The mission w
m
of the system in the simulation (light
green line in Fig. 6) was to follow a hallway with-
out colliding with the wall. Noise was added to the
wheels to simulate slippage and/or actuator degener-
ation.
0 1 2 3 4 5
0
1
2
3
4
5
6
7
8
9
10
(a)
0 1 2 3 4 5
0
1
2
3
4
5
6
7
8
9
10
X−Distance
Y−Distance
(b)
Figure 6: Simulation Setup. Left image shows the mission
trajectory (light green line) of the robot traveling down a
hallway (red line). Right image shows the particles used
for the state estimation for every 40th time step (blue stars)
together with the safe area (dotted red line).
To compute the dependability the distance between
the mission trajectory and the robot trajectory (d
m
(t))
together with the distance between the robot trajec-
tory and the safe area (red line in Fig. 6) relative to
the distance between the mission trajectory and the
safe area (d
S
(t)) was used to compute the depend-
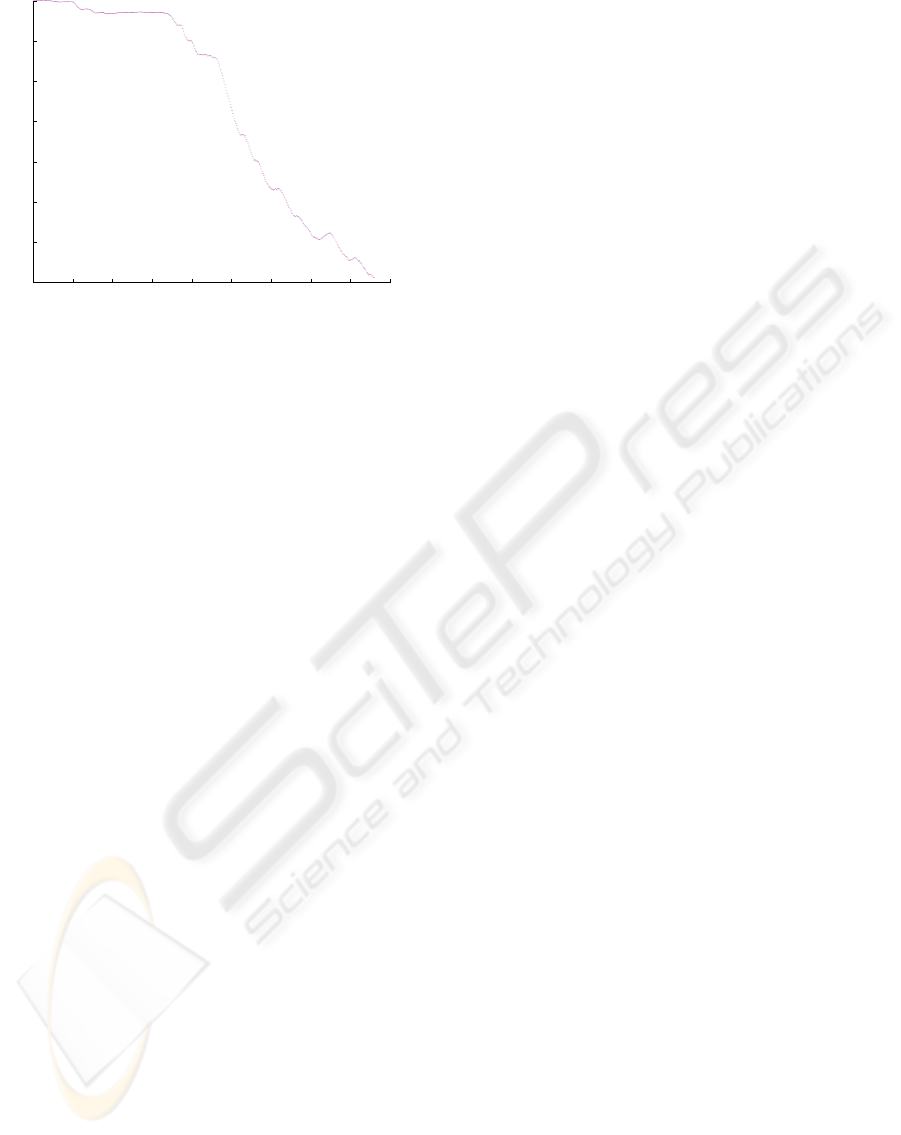
ability as proposed above. The resulting dependabil-
ity can be seen in Fig 7. Since a diverge from the
mission trajectory also always decreases the distance
to the safe area both effects sum up.
In addition to just estimating the system state, the par-
ticle filter was also used to predict the future values of
the system state and as thus the future dependability
of the system. In this setup only the prediction for the
next time step was used.
5 CONCLUSIONS
Dependability is of great importance for autonomous
mobile systems. Not only for measuring the depend-
ability, but also for comparing it to other missions of
the same system or other systems aswell, a formal
definition of dependability is important. The defini-
tion of dependability used in this paper is based on a
mathematical description of the system and its behav-
ior. This property was used in this paper to propose
a method for estimating the dependability of an au-
tonomous mobile system using a particle filter.
BEHAVIOR BASED DEPENDABILITY ESTIMATION - Estimating the Dependability of Autonomous Mobile Systems
using Predictive Filter
141

0 5 10 15 20 25 30 35 40 45
0.93
0.94
0.95
0.96
0.97
0.98
0.99
1
Time
Dependability
Figure 7: Measured (red) and predicted (blue) dependability
of the autonomous mobile system.
REFERENCES
Arlat, J., Aguera, M., Amat, L., Crouzet, Y., Fabre, J.-C.,
Laprie, J.-C., Martins, E., and Powell, D. (1990). Fault
injection for dependability validation: A methodology
and some applications. IEEE Transactions on Soft-
ware Engineering, 16(2):166–182.
Arulampalam, M. S., Maskell, S., Gordon, N., and Clapp,
T. (2002). A tutorial on particle filters for on-
line nonlinear/non-gaussian bayesian tracking. Signal
Processing, IEEE Transactions on [see also Acous-
tics, Speech, and Signal Processing, IEEE Transac-
tions on], 50(2):174–188.
Avizienis, A., Laprie, J.-C., and Randell, B. (2004a). De-
pendability and its threats: A taxonomy.
Avizienis, A., Laprie, J.-C., Randell, B., and Landwehr, C.
(2004b). Basic concepts and taxonomy of dependable
and secure computing. IEEE Trans. on Dependable
and Secure Computing, 1(1):11–33.
Badreddin, E. (1999). Safety and dependability of mecha-
tronics systems. In Lecture Notes. ETH Z¨urich.
Brown, A., Chung, L., and Patterson, D. A. (2002). Includ-
ing the human factor in dependability benchmarks. In
Proceedings of the DSN Workshop on Dependability
Benchmarking.
Candea, G. (2003). The basics of dependability.
Carter, W. (1982). A time for reflection. In Proc. 12th
Int. Symp. on Fault Tolerant Computing (FTCS-12).
FTCS-12) IEEE Computer Society Press Santa Mon-
ica.
Chen, Z. (2003). Bayesian filtering: From kalman filters to
particle filters, and beyond. Technical report, McMas-
ter University.
Cukier, M. and Smidts, C. S. (2002). Using bayesian theory
for estimating dependability benchmark measures. In
Proceedings of the DSN Workshop on Dependability
Benchmarking.
Department of Defense, U. S. o. A. (1970). Military stan-
dard - definitions of terms for reliability and maintain-
ability. Technical Report MIL-STD-721C.
Dewsbury, G., Sommerville, I., Clarke, K., and Rounce-
field, M. (2003). A dependability model for domestic
systems. In SAFECOMP, pages 103–115.
Dubrova, E. (2006). Fault tolerant design: An introduction.
Draft.
Kanoun, K., Madeira, H., and Aria, J. (2002). A framework
for dependability benchmarking. In Proceedings of
the DSN Workshop on Dependability Benchmarking.
Laprie, J. C. (1992). Dependability. Basic Concepts and
Terminology. Ed. Springer Verlag.
Mukherjee, A. and Siewiorek, D. P. (1997). Measuring
software dependability by robustness benchmarking.
IEEE Trans. Softw. Eng., 23(6):366–378.
Randell, B. (2000). Turing Memorial Lecture: Facing up to
faults. 43(2):95–106.
R¨udiger, J., Wagner, A., and Badreddin, E. (2007a). Behav-
ior based definition of dependability for autonomous
mobile systems. European Control Conference 2007.
Kos, Greece.
R¨udiger, J., Wagner, A., and Badreddin, E. (2007b). Be-
havior based description of dependability - defining a
minium set of attributes for a behavioral description
of dependability. ICINCO.
Rus, I., Basili, V., Zelkowitz, M., and Boehm, B. (2002).
Empirical evaluation of techniques and methods used
for achieving and assessing software high dependabil-
ity. In Proceedings of the DSN Workshop on Depend-
ability Benchmarking.
Willems, J. (1991). Paradigms and puzzles in the theory of
dynamical systems. Automatic Control, IEEE Trans-
actions on, 36(3):259–294.
Wilson, D., Murphy, B., and Spainhower, L. (2002).
Progress on defining standardized classes for compar-
ing the dependability of computer systems.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
142