
RECURSIVE BIAS-COMPENSATING ALGORITHM FOR THE
IDENTIFICATION OF DYNAMICAL BILINEAR SYSTEMS IN THE
ERRORS-IN-VARIABLES FRAMEWORK
T. Larkowski, J. G. Linden, B. Vinsonneau and K. J. Burnham
Control Theory and Applications Centre, Coventry University, Prior Street, Coventry, U.K.
Keywords:
Bias compensation, Bilinear systems, Errors-in-variables, Recursive estimation, Regularization, System iden-
tification.
Abstract:
The paper investigates a recursive approach for the bias compensating least squares (BCLS) technique. The
method presented is applied to the problem of on-line identification of single-input single-output bilinear
models in the errors-in-variables framework. Within this framework the recursive bilinear BCLS algorithm is
realized when a bilinear Frisch scheme (BFS) is iteratively applied for the estimation of the parameters of an
exemplary bilinear system, giving rise to the exact recursive BFS (ERBFS) method. Moreover, a further exten-
sion of the ERBFS incorporating Tikhonov regularization with variable exponential weighting is considered
and this is shown to be beneficial in the initial period of the identification procedure.
1 INTRODUCTION
The errors-in-variables (EIV) framework addresses
the identification of dynamical systems where both
the input and the output signals are corrupted by the
measurement noise (S¨oderstr¨om, 2007). The EIV ap-
proaches are found to be of considerable benefit when
the underlying physical laws characterizing the sys-
tem are of a prime interest, as opposed to the predic-
tion of the external signals (S¨oderstr¨om et al., 2002).
In this case, the classical methods based on the least
squares (LS) principle such as recursive LS (RLS)
or the Kalman filter (Ikonen and Najim, 2002) are
shown to yield estimates of the system parameters that
are asymptotically biased and, therefore, inconsistent
(Zheng, 1998; S¨oderstr¨om, 2007).
In the field of modelling for nonlinear systems, the
bilinear system (BS) models have been used to ad-
vantage in various practical applications, e.g. control
plants, biological and chemical phenomena, earth and
sun science, nuclear fission, fault diagnosis and su-
pervision, see (Mohler, 1991; Mohler and Khapalov,
2000) or (Ekman, 2005). Due mainly to the fact that
BS models are so widely applicable has prompted the
need to extend the EIV approaches developed for lin-
ear systems to encompass the BS case.
Recently, a technique for off-line compensation
of the bias in the case of dynamical BS, i.e. the bi-
linear bias compensating LS (BBCLS) scheme has
been proposed (Larkowski et al., 2007), upon which
a bilinear Frisch scheme (BFS) has been constructed
(Larkowski et al., 2008). The focus of this paper is
the extension of the BBCLS along with the BFS for
the purpose of on-line system identification. The pro-
posed approach consists of a recursively performed
update and bias compensation procedure for the data
covariance matrices, whilst the BFS equations are ap-
plied in an iterative manner at each recursion step.
Moreover, a further extension of the BFS incorporat-
ing the Tikhonov regularization (TR) technique with
a variable exponential weighting is considered. It is
shown via simulation studies that use of TR can be of
considerable benefit in the initial period of the identi-
fication procedure.
The paper is organized as follows: in the second
section the mathematical representation of the EIV
BS together with the assumptions stated and the no-
tation used are introduced. The third section presents
a brief review of the BBCLS and the BFS techniques.
In section four a recursive implementation of the BB-
CLS method is proposed. Subsequently, within the
BBCLS framework the BFS technique is applied re-
sulting in the exact recursive BFS (ERBFS) algo-
rithm. The section ends with an extension of the
ERBFS that incorporates the TR technique. Section
five presents the results of a numerical simulation
study involving the proposed algorithms, whilst the
overall conclusions and the further work are summa-
rized in section six.
38
Larkowski T., G. Linden J., Vinsonneau B. and J. Burnham K. (2008).
RECURSIVE BIAS-COMPENSATING ALGORITHM FOR THE IDENTIFICATION OF DYNAMICAL BILINEAR SYSTEMS IN THE ERRORS-IN-
VARIABLES FRAMEWORK.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 38-45
DOI: 10.5220/0001496000380045
Copyright
c
SciTePress
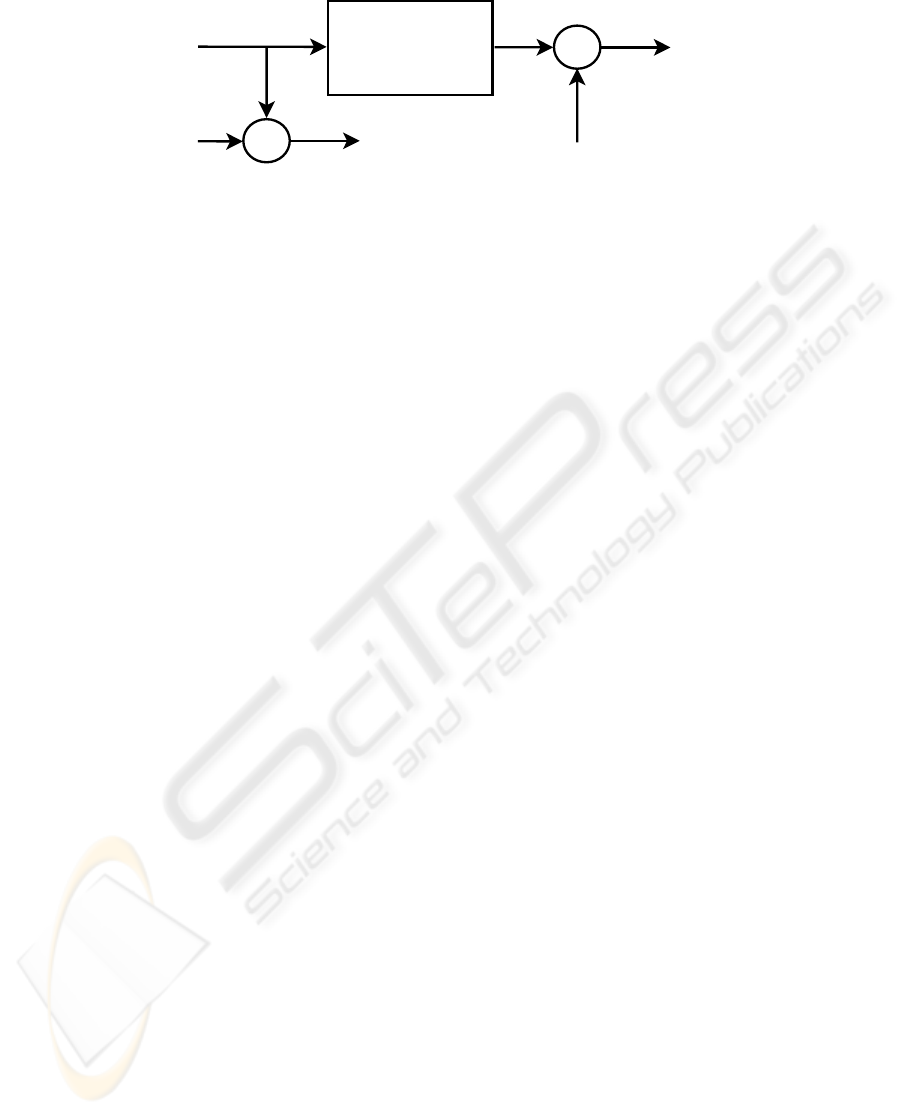
Σ
Σ
u
0
k
y
0
k
˜u
k
˜y
k
y
k
u
k
Bilinear
system
Figure 1: The basic setup for the EIV BS.
2 ASSUMPTIONS AND
NOTATION
Consider a discrete time-invariant single-input single-
output (SISO) class of BS that can be represented by
the following input/output difference equation
A(q
−1
)y
0
k
=B(q
−1
)u
0
k
+
p
∑
i=1
r
∑
j=1
η
ij
u
0
k−i
y
0
k− j
(1)
with the polynomials A(q
−1
) and B(q
−1
) given by
A(q
−1
) ,1 + a
1
q
−1
+ ... + a
n
a
q
−n
a
(2a)
B(q
−1
) ,b
1
q
−1
+ ... + b
n
b
q
−n
b
(2b)
where r ≤ n
a
, p ≤ n
b
≤ n
a
, q
−1
is the backward shift
operator, defined by x
k
q
−1
, x
k−1
and u
0
k
, y
0
k
are the
noise-free input and output sequences, respectively. A
diagrammatic illustration of the typical EIV setup for
a SISO BS is depicted in Figure 1.
The BS can be classified into three main cate-
gories, see (Pearson, 1999) for more details, namely:
a) subdiagonal η
ij
= 0 ∀ j > i; b) diagonal η
ij
=
0 ∀ j 6= i; and c) superdiagonal η
ij
= 0 ∀ j < i. Noting
that both the subdiagonal and superdiagonal cases in-
clude the diagonal case, reference will be solely made
here to the diagonal BS (DBS) case for the remainder
of the paper. This is due to the fact that DBS exhibit
some crucial properties of interest, see (Rao and Gabr,
1984; Liu, 1992) or (Kotta and Nomm, 2003) for a de-
tailed discussion. At the same time DBS are possibly
the most commonly utilized class of BS for the pur-
pose of industrial applications, see (Burnham, 1991;
Yu, 1996; Martineau et al., 2004).
Without loss of generality, the case when all the
diagonal terms in the system (1) are present is consid-
ered here with their number given as n
η
= p
2
where
r = p. The following assumptions are introduced:
A1. The DBS is time-invariant, asymptotically stable,
strictly stationary, observable and controllable.
A2. The system structure, i.e. n
a
, n
b
, p, is known a
priori.
A3. The true input u
0
k
∼ N (0, σ
u
0
) is white, persis-
tently exciting and of sufficiently high order.
A4. Corrupting input/output noises ˜u
k
∼N (0,σ
˜u
) and
˜y
k
∼ N (0,σ
˜y
) of unknown variances are addi-
tive, white, mutually uncorrelated and uncorre-
lated with the noise free signals u
0
k
and y
0
k
, re-
spectively.
Acknowledging A4, it is implied that the measured
input and output can be decomposed into their noise
free and noise contributions, i.e.
u
k
,u
0
k
+ ˜u
k
(3a)
y
k
,y
0
k
+ ˜y
k
(3b)
where k denotes the discrete time index. The identifi-
cation problem consists of determining the vector
ϑ
T
,
θ
T
σ
˜u
σ
˜y
∈ R
n
θ
+2
(4)
where θ ∈ R
n
θ
is the parameter vector with n
θ
=
n
a
+ n
b
+ n
η
and σ
˜u
, σ
˜y
are the input and output noise
variances, respectively. The parameter vector is de-
fined as:
θ ,
a
b
η
a ,
a
1
.
.
.
a
n
a
b ,
b
1
.
.
.
b
n
b
η ,
η
11
.
.
.
η
pp
(5)
with a ∈ R
n
a
, b ∈ R
n
b
, η ∈ R
n
η
where the extended
parameter vector
¯
θ is given by
¯
θ ,
¯a
b
η
∈ R
n
θ
+1
¯a ,
1
a
∈ R
n
a
+1
(6)
The regressor vectors for the measured data, noise-
free data and noise are defined, respectively, as:
ϕ
k
,
ϕ
y
k
ϕ
u
k
ϕ
ρ
k
ϕ
0
k
,
ϕ
y
0,k
ϕ
u
0,k
ϕ
ρ
0,k
˜
ϕ
k
,
˜
ϕ
y
k
˜
ϕ
u
k
˜
ϕ
ρ
k
(7)
where
ϕ
y
k
,
−y
k−1
.
.
.
−y
k−n
a
ϕ
u
k
,
u
k−1
.
.
.
u
k−n
b
ϕ
ρ
k
,
y
k−1
u
k−1
.
.
.
y
k−p
u
k−p
RECURSIVE BIAS-COMPENSATING ALGORITHM FOR THE IDENTIFICATION OF DYNAMICAL BILINEAR
SYSTEMS IN THE ERRORS-IN-VARIABLES FRAMEWORK
39

ϕ
y
0,k
,
−y
0
k−1
.
.
.
−y
0
k−n
a
ϕ
u
0,k
,
u
0
k−1
.
.
.
u
0
k−n
b
ϕ
ρ
0,k
,
y
0
k−1
u
0
k−1
.
.
.
y
0
k−p
u
0
k−p
˜
ϕ
y
k
,
− ˜y
k−1
.
.
.
˜y
k−n
a
˜
ϕ
T
u
k
,
˜u
k−1
.
.
.
˜u
k−n
b
˜
ϕ
T
ρ
k
,
˜
ρ
k−1,k−1
.
.
.
˜
ρ
k−p,k−p
with ϕ
k
, ϕ
0
k
,
˜
ϕ
k
∈ R
n
θ
, ϕ
y
k
, ϕ
y
0,k
,
˜
ϕ
y
k
∈ R
n
a
, ϕ
u
k
,
ϕ
u
0,k
,
˜
ϕ
u
k
∈ R
n
b
, ϕ
ρ
k
, ϕ
ρ
0,k
,
˜
ϕ
ρ
k
∈ R
n
η
and
˜
ρ
k−i,k− j
denoting the noise contribution corresponding to the
bilinear product terms of the regressor vector ϕ
ρ
k
. In
agreement with (7), the extended regressor vectors are
given by
¯
ϕ
k
,
−y
k
ϕ
k
¯
ϕ
0
k
,
−y
0
k
ϕ
0
k
˜
¯
ϕ
k
,
− ˜y
k
˜
ϕ
k
(8)
where
¯
ϕ
k
,
¯
ϕ
0
k
,
˜
¯
ϕ
k
∈ R
n
θ
+1
.
3 A BRIEF REVIEW OF BBCLS
AND BFS
3.1 BBCLS
The BBCLS algorithm for the class of DBS comprises
of equations (9), (10) and (11), see (Larkowski et al.,
2007). These correspond to the bilinear bias compen-
sation rule, the noise covariance matrix and the noise
‘variance’ of the bilinear terms, respectively, i.e.
ˆ
θ
BBCLS
,
Σ
ϕϕ
− Σ
˜
ϕ
˜
ϕ
−1
Σ
ϕy
(9)
Σ
˜
ϕ
˜
ϕ
,
σ
˜y
I
n
a
0 0
0 σ
˜u
I
n
b
0
0 0 σ
˜
ρ
I
n
η
(10)
σ
˜
ρ
, σ
u
σ
˜y
+ σ
y
σ
˜u
− σ
˜u
σ
˜y
(11)
where σ
u
, E[u
k
] and σ
y
, E[y
k
] are the expected val-
ues of the measured system input and output signals
and (ˆ·) denotes an estimate. It is noted, that in the re-
mainder of the paper, the expression Σ
ab
will be used
as general notation for the correlation matrix of vec-
tors a
k
and b
k
, i.e. Σ
ab
= E[a
k
b
T
k
]. Equation (9) can
be alternatively restated as
ˆ
θ
BBCLS
=
ˆ
θ
LS
+ Σ
−1
ϕϕ
Σ
˜
ϕ
˜
ϕ
ˆ
θ
BBCLS
(12)
where
ˆ
θ
LS
denotes the LS estimate. It is implied from
the BBCLS algorithm that the knowledge regarding
noise variances corrupting input/output of a system
together with variances of measured input/output sig-
nals is sufficient to obtain unbiased estimates of the
true system parameters.
3.2 BFS
The Frisch scheme is a technique that allows the di-
rect estimation of the input/output noise variances to-
gether with the parameters of a system (Beghelli et al.,
1990; S¨oderstr¨om, 2006). As consequence, the a pri-
ori knowledge regarding the values of σ
˜u
and σ
˜y
is
not required leading to a wider practical applicabil-
ity. The extension of the FS, in the framework of the
BBCLS technique, for the class of DBS has been pro-
posed in (Larkowski et al., 2008). Define the parti-
tioned extended data covariance matrix
Σ
¯
ϕ
¯
ϕ
,
Σ
¯
ϕ
y
¯
ϕ
y
Σ
T
ϕ
u
¯
ϕ
y
Σ
T
ϕ
ρ
¯
ϕ
y
Σ
ϕ
u
¯
ϕ
y
Σ
ϕ
u
ϕ
u
Σ
T
ϕ
ρ
ϕ
u
Σ
ϕ
ρ
¯
ϕ
y
Σ
ϕ
ρ
ϕ
u
Σ
ϕ
ρ
ϕ
ρ
(13)
where Σ
¯
ϕ
y
¯
ϕ
y
∈ R
(n
a
+1)×(n
a
+1)
, Σ
ϕ
u
¯
ϕ
y
∈ R
n
b
×(n
a
+1)
,
Σ
ϕ
u
ϕ
u
∈ R
n
b
×n
b
, Σ
ϕ
ρ
¯
ϕ
y
∈ R
n
η
×(n
a
+1)
, Σ
ϕ
ρ
ϕ
u
∈ R
n
η
×n
b
and Σ
ϕ
ρ
ϕ
ρ
∈ R
n
η
×n
η
. The BFS consists of three main
phases, i.e. calculation of the maximal admissible
value for σ
˜u
, denoted σ
max
˜u
(14), determination of a
functional relationship between σ
˜y
and σ
˜u
(16a) and
the specification of a cost function to find a unique
value of σ
˜u
(18a). The quantity σ
max
˜u
is given by:
σ
max
˜u
, λ
min
(A
∗
1
) (14)
where λ
min
(A
∗
1
) denotes the least eigenvalue of the
matrix A
∗
1
, and max(·) is the maximum operator. The
matrix A
∗
1
is defined as:
A
∗
1
, A
1
− B
1
Σ
−1
¯
ϕ
y
¯
ϕ
y
B
T
1
(15a)
with
A
1
,
Σ
ϕ
u
ϕ
u
Σ
T
ϕ
ρ
ϕ
u
Σ
ϕ
ρ
ϕ
u
Σ
ϕ
ρ
ϕ
ρ
B
1
,
Σ
ϕ
u
¯
ϕ
y
Σ
ϕ
ρ
¯
ϕ
y
(15b)
The functional relationship between σ
˜y
and σ
˜u
is
described by
σ
˜y
, λ
min
(A
∗
2
) (16a)
where
A
∗
2
, A
2
−B
2
(Σ
ϕ
u
ϕ
u
−σ
˜u
I
n
b
)
−1
B
T
2
(16b)
with
A
2
,
Σ
¯
ϕ
y
¯
ϕ
y
Σ
T
ϕ
ρ
¯
ϕ
y
Σ
ϕ
ρ
¯
ϕ
y
Σ
ϕ
ρ
ϕ
ρ
−σ
y
σ
˜u
I
n
η
B
2
,
Σ
T
ϕ
u
¯
ϕ
y
Σ
ϕ
ρ
ϕ
u
(16c)
The cost function utilized is based on the Yule-
Walker equations, see (Diversi et al., 2006) for de-
tails. The instrumental vector (S¨oderstr¨om and Sto-
ica, 1994) for the measured data is defined as:
¯
ϕ
IV
k
,
¯
ϕ
k−n
a
−1
∈ R
n
θ+1
×1
(17)
Using (17) the corresponding cost function is formu-
lated as:
J(
ˆ
¯
θ) , kΣ
¯
ϕ
IV
¯
ϕ
ˆ
¯
θk
2
2
(18a)
such that
J(
ˆ
¯
θ) = 0 ⇔
ˆ
¯
θ =
¯
θ (18b)
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
40
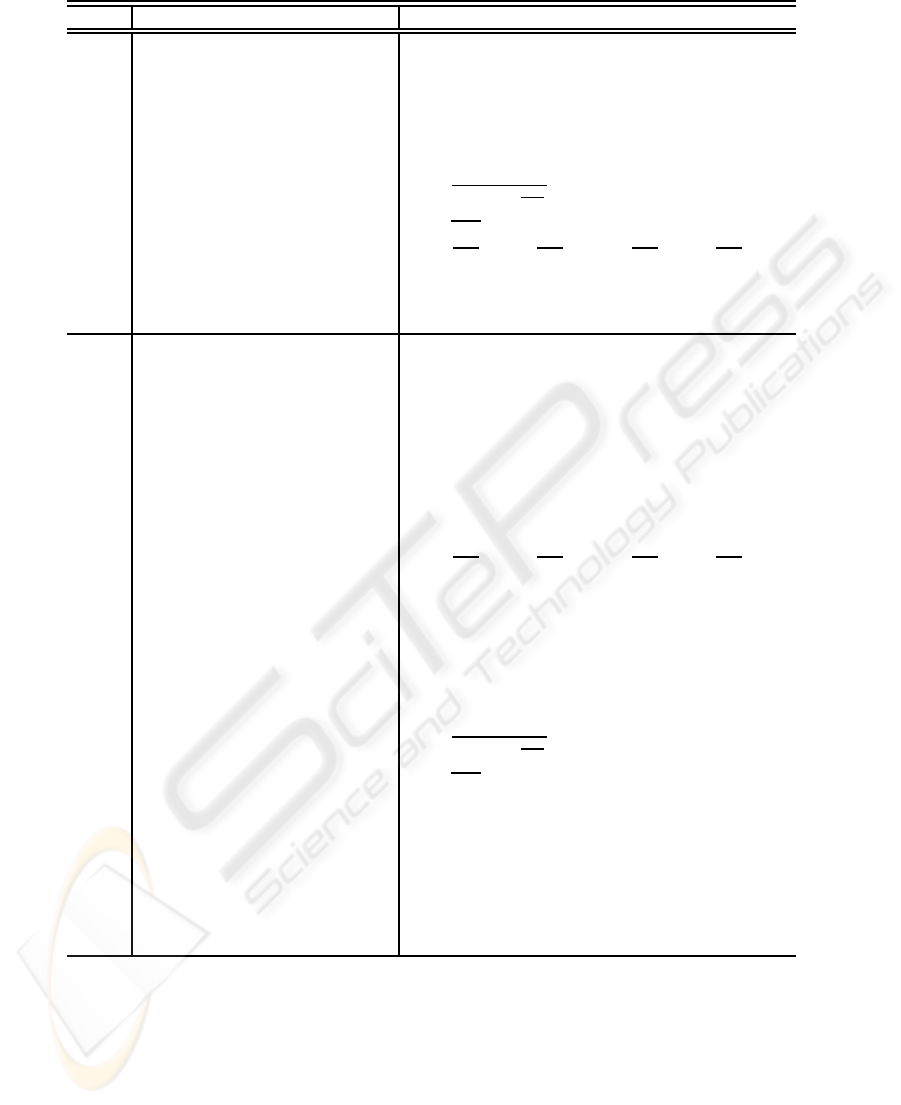
Table 1: Summary of the ERBFS algorithm.
Step Description Procedure
1 Choose λ
k
and j 0 < λ
k
< 1, j = 2n
a
+ 1
2 RLS initialization:
ˆ
θ
LS
n
θ
= 0, P
n
θ
= 10
3
I
n
θ
,
ˆ
σ
k
u
= 0,
ˆ
σ
k
y
= 0
2.1 RLS loop start for k = n
θ
+ 1... j
2.2 Data weighting γ
k
= 1/k
Computation of:
2.3 L
k
,
ˆ
θ
LS
k
, P
k
L
k
=
P
k−1
ϕ
k
ϕ
T
k
P
k−1
ϕ
k
+
1−γ
k
γ
k
,
ˆ
θ
LS
k
=
ˆ
θ
LS
k−1
+ L
k
y
k
− ϕ
T
k
ˆ
θ
LS
k−1
P
k
=
1
1−γ
k
P
k−1
− L
k
ϕ
T
k
P
k−1
2.4
ˆ
σ
k
u
,
ˆ
σ
k
y
ˆ
σ
k
u
=
k−1
k
ˆ
σ
k−1
u
+
1
k−1
u
2
k
,
ˆ
σ
k
y
=
k−1
k
ˆ
σ
k−1
y
+
1
k−1
y
2
k
2.5 Σ
k
ϕ
ρ
¯
ϕ
y
Σ
k
¯
ϕ
¯
ϕ
= Σ
k−1
¯
ϕ
¯
ϕ
+ γ
k
¯
ϕ
k
¯
ϕ
T
k
− Σ
k−1
¯
ϕ
¯
ϕ
2.6 RLS loop end end
3 BBCLS and BFS initialization Σ
k
¯
ϕ
IV
¯
ϕ
= 0,
ˆ
σ
max
˜u
= λ
min
(A
∗
1, j
)
3.1 Recursive BBCLS start for k = j+ 1... N
3.2 Data weighting γ
k
= 1/k
3.3 Iterative BFS start
Computation of:
3.3.1 Σ
k
¯
ϕ
IV
¯
ϕ
Σ
k
¯
ϕ
IV
¯
ϕ
= Σ
k−1
¯
ϕ
IV
¯
ϕ
+ γ
k
¯
ϕ
IV
k
¯
ϕ
T
k
− Σ
k−1
¯
ϕ
IV
¯
ϕ
3.3.2
ˆ
σ
k
˜u
ˆ
σ
k
˜u
= arg min
ˆ
σ
k
˜u
J(
ˆ
¯
θ
k
)
3.3.3
ˆ
σ
k
u
,
ˆ
σ
k
y
ˆ
σ
k
u
=
k−1
k
ˆ
σ
k−1
u
+
1
k−1
u
2
k
,
ˆ
σ
k
y
=
k−1
k
ˆ
σ
k−1
y
+
1
k−1
y
2
k
3.3.4 Σ
k
¯
ϕ
¯
ϕ
Σ
k
¯
ϕ
¯
ϕ
= Σ
k−1
¯
ϕ
¯
ϕ
+ γ
k
¯
ϕ
k
¯
ϕ
T
k
− Σ
k−1
¯
ϕ
¯
ϕ
3.3.5 A
k
2
, B
k
2
A
k
2
=
"
Σ
k
¯
ϕ
y
¯
ϕ
y
(Σ
k
ϕ
ρ
¯
ϕ
y
)
T
Σ
k
ϕ
ρ
¯
ϕ
y
Σ
T
ϕ
ρ
ϕ
ρ
−
ˆ
σ
k
y
ˆ
σ
k
˜u
I
n
η
#
, B
k
2
=
"
(Σ
k
ϕ
u
¯
ϕ
y
)
T
Σ
k
ϕ
ρ
ϕ
u
#
3.3.6 A
∗
2,k
A
∗
2,k
= A
k
2
−B
k
2
(Σ
k
ϕ
u
ϕ
u
−
ˆ
σ
k
˜u
I
n
b
)
−1
(B
k
2
)
T
3.3.7
ˆ
σ
k
˜y
ˆ
σ
k
˜y
= λ
min
(A
∗
2,k
)
3.4 Iterative BFS end
3.5 L
k
,
ˆ
θ
LS
k
, P
k
L
k
=
P
k−1
ϕ
k
ϕ
T
k
P
k−1
ϕ
k
+
1−γ
k
γ
k
,
ˆ
θ
LS
k
=
ˆ
θ
LS
k−1
+ L
k
y
k
− ϕ
T
k
ˆ
θ
LS
k−1
P
k
=
1
1−γ
k
P
k−1
− L
k
ϕ
T
k
P
k−1
3.6
ˆ
σ
k
˜
ρ
ˆ
σ
k
˜
ρ
=
ˆ
σ
k
u
ˆ
σ
k
˜y
+
ˆ
σ
k
y
ˆ
σ
k
˜u
−
ˆ
σ
k
˜u
ˆ
σ
k
˜y
3.7 Σ
k
˜
ϕ
˜
ϕ
Σ
k
˜
ϕ
˜
ϕ
=
ˆ
σ
k
˜y
I
n
a
0 0
0
ˆ
σ
k
˜u
I
n
b
0
0 0
ˆ
σ
k
˜
ρ
I
n
η
3.8 Bias compensation
ˆ
θ
BBCLS
k
=
ˆ
θ
LS
k
+ P
k
Σ
k
˜
ϕ
˜
ϕ
ˆ
θ
BBCLS
k−1
3.9 Recursive BBCLS end end
4 RECURSIVE BBCLS WITH
ITERATIVE BFS
In this section a recursive BBCLS (RBBCLS) algo-
rithm is developed, which comprises the recursive
update of the data and instrumental covariance ma-
trices, whilst the bias compensation procedure is re-
cursively applied to the data covariance matrix only.
Furthermore, an application of the BFS at each iter-
ation step is described with an additional extension
incorporating the TR technique. It is to be noted that
the RBBCLS method can be interpreted in the frame-
work of the iterative bias compensating LS (BCLS)
approaches, see e.g. (Zheng, 1998) and (Zheng, 2000)
for more details.
RECURSIVE BIAS-COMPENSATING ALGORITHM FOR THE IDENTIFICATION OF DYNAMICAL BILINEAR
SYSTEMS IN THE ERRORS-IN-VARIABLES FRAMEWORK
41

4.1 Recursive BBCLS
The normalized recursive updates of the instrumental
and data covariance matrices are given by the follow-
ing equations, see (Ljung, 1999)
Σ
k
¯
ϕ
¯
ϕ
= Σ
k−1
¯
ϕ
¯
ϕ
+ γ
k
¯
ϕ
k
¯
ϕ
T
k
− Σ
k−1
¯
ϕ
¯
ϕ
(19a)
Σ
k
¯
ϕ
IV
¯
ϕ
= Σ
k−1
¯
ϕ
IV
¯
ϕ
+ γ
k
¯
ϕ
IV
k
¯
ϕ
T
k
− Σ
k−1
¯
ϕ
IV
¯
ϕ
(19b)
with
γ
k
=
Σ
k
i=1
β
k,i
−1
=
γ
k−1
λ
k
+ γ
k−1
(20)
where the i-th data is weighted at the discrete time k
according to the following rule
β
k,i
= λ
k
β
k−1,i
for 0 ≤ i ≤ k − 1 (21)
and β
k,k
= 1. It is to be noted that (20) simplifies
either to 1/k in the case of no adaptivity, i.e. when
λ
k
= 1 or to 1− λ when the exponential forgetting is
used, i.e. λ
k
= λ with 0 < λ < 1.
Assuming that the input/output noise variances,
i.e. σ
˜u
and σ
˜y
are known a priori or can be estimated,
allows application of the BBCLS algorithm to the re-
cursively computed estimate of the parameter vector,
i.e.
ˆ
θ
BBCLS
k
=
ˆ
θ
LS
k
+ P
k
Σ
˜
ϕ
˜
ϕ
ˆ
θ
BBCLS
k−1
(22a)
Σ
˜
ϕ
˜
ϕ
=
σ
˜y
I
n
a
0 0
0 σ
˜u
I
n
b
0
0 0
ˆ
σ
k
˜
ρ
I
n
η
(22b)
ˆ
σ
k
˜
ρ
=
ˆ
σ
k
u
σ
˜y
+
ˆ
σ
k
y
σ
˜u
− σ
˜u
σ
˜y
(22c)
ˆ
σ
k
u
=
k− 1
k
ˆ
σ
k−1
u
+
1
k− 1
u
2
k
(22d)
ˆ
σ
k
y
=
k− 1
k
ˆ
σ
k−1
y
+
1
k− 1
y
2
k
(22e)
L
k
=
P
k−1
ϕ
k
ϕ
T
k
P
k−1
ϕ
k
+
1−γ
k
γ
k
(22f)
ˆ
θ
LS
k
=
ˆ
θ
LS
k−1
+ L
k
y
k
− ϕ
T
k
ˆ
θ
LS
k−1
(22g)
P
k
=
1
1− γ
k
P
k−1
− L
k
ϕ
T
k
P
k−1
(22h)
It is remarked that whilst the input/output noise vari-
ances are postulated to be known, the noise ‘variance’
corresponding to the bilinear terms (22c) is required
to be recursivelyapproximated at each time step. This
involves the recursive estimation of the variances of
the input/output signals, i.e. (22d) and (22e) (Young,
1984). Note that due to assumptions A1 and A3, see
(Pearson, 1999) for more details, the mean values of
the input/output signals do not explicitly appear in ex-
pressions (22d) and (22e) since they are both null.
4.2 Iterative BFS
Utilization of the recursively evaluated data and in-
strumental covariance matrices from the RBBCLS al-
gorithm allows the application of the BFS at each
recursion. Thus it is possible not only to estimate
the input/output noise variances but also to conduct
the noise compensation procedure given by (22a), see
(Linden et al., 2007) for more details regarding the
linear case. This results in the ERBFS algorithm
which is summarized in Table 1. It is to be noted that
ERBFS is rather expensive from the computational
point of view. However, with reference to Table 1, if
the time allowed for the calculation of
ˆ
σ
k
˜u
at step 3.3.2
is bounded, the algorithm at least satisfies the prin-
ciples of a recursive estimation scheme (Ljung and
S¨oderstr¨om, 1987; Ljung, 1999).
4.3 Regularized BFS
In the case when a priori knowledge regarding the
value of the input noise variance is available,or can be
approximately anticipated, a regularization technique
may be utilized. The regularization method consid-
ered here is that of TR which forces the estimate to-
wards a pre-specified value
ˆ
σ
∗
˜u
controlled by the pa-
rameter ω (Hansen, 2001). The incorporation of TR
into the cost function given by (18a) results in the fol-
lowing regularized cost function
J(
ˆ
¯
θ,ω,
ˆ
σ
∗
˜u
), ωkΣ
¯
ϕ
IV
¯
ϕ
ˆ
¯
θk
2
2
+ (1−ω)k
ˆ
σ
∗
˜u
−
ˆ
σ
˜u
k
2
2
(23)
Note that (23) reduces to (18a) for ω = 1. Further-
more, it may be beneficial to consider a variable con-
trolling parameter, i.e. ω
k
, such that the impact of
the regularization is significant at the beginning of the
identification procedure but gradually diminishes as a
function of the incoming data stream. It is proposed
to realize the concept as follows
ω
k
= e
−
ς
k
(24)
where ς is a user defined parameter describing the rate
at which the impact of the regularization diminishes.
This choice allows the potential bias introduced by
regularization (Hansen, 2001) to be alleviated as time
progresses. With reference to Table 1, the introduc-
tion of regularization requires the additional setting of
the parameter ς at step 3, the subsequent implemen-
tation of equation (24) between steps 3.3.1 and 3.3.2
and replacement of the cost function J
k
(
ˆ
¯
θ
k
) from 3.3.2
by J(
ˆ
¯
θ
k
,ω
k
,
ˆ
σ
∗
˜u
).
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
42

5 SIMULATION STUDIES
This section provides a numerical evaluation and
comparison of the proposed ERBFS algorithm with
the RLS and the off-line BFS. The SISO DBS system
used in the simulations with n
a
= 2, n
b
= n
η
= 1 is
simulated for N = 5000. It is described by the follow-
ing difference equation
y
0
k
= 1.2y
0
k−2
− 0.9y
0
k−1
+ 0.6u
0
k−1
+
0.1y
0
k−1
u
0
k−1
(25)
The input is generated by
u
0
k
∼ N (0,0.5) (26)
The variances of the input and output noises are
selected as σ
˜u
= 0.05 and σ
˜y
= 0.16, respectively,
in order to yield an approximately equal signal-to-
noise ratio (SNR) on both input and output, i.e.
SNR
u
≈ SNR
y
≈ 10[dB]. In the case of the ERBFS
and the regularized ERBFS (RERBFS) the minimiza-
tion procedure from step 3.3.2 (see Table 1) is re-
stricted to a maximum of 10 iterations. The parameter
λ
k
is set to unity, i.e. no adaptivity, for all evaluated
algorithms.
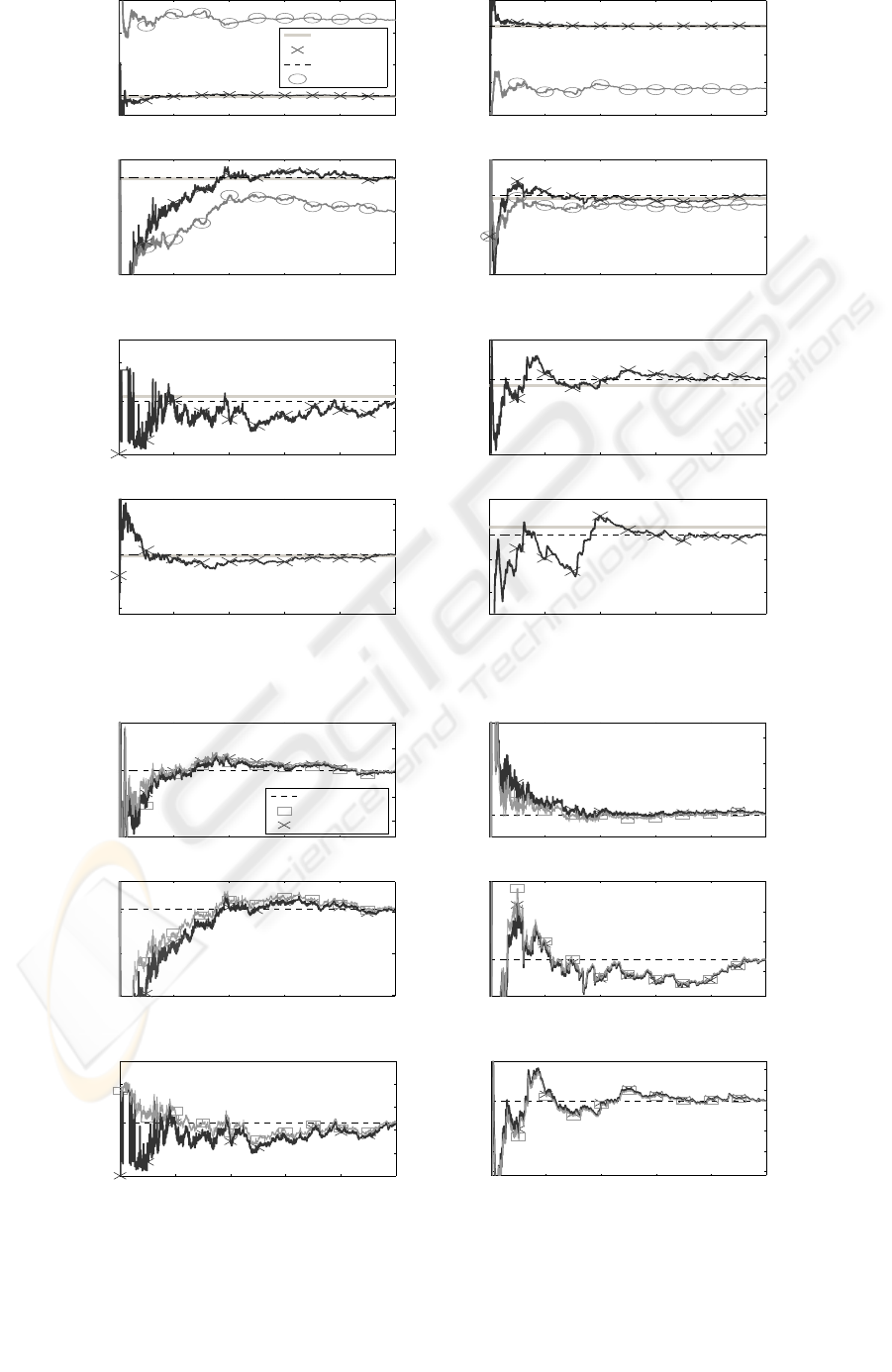
Considering the results presented in Figure 2,
where the ERBFS is compared with its off-line coun-
terpart and the RLS, the following observations are
made:
a) RLS yields estimates that are asymptotically bi-
ased for the case of all system parameters.
b) The estimate of the vector ϑ obtained via the off-
line BFS is quite close to its true value.
c) The EBFS achieved virtually identical estimates
as the off-line BFS at the last recursion step, i.e.
k = N.
d) Estimates given by EBFS converge to their off-
line counterparts obtained by the BFS algorithm
over the succesive recursions.
e) There is a clear correlation between the quality of
the estimated variances of the input/output signals
and the quality of the estimated input/output noise
variances which, subsequently, has an impact on
the estimates of the system parameters.
f) The ERBFS encountered some difficulties in the
estimation of the input noise variance in the ini-
tial part of the identification procedure, i.e. up to
about first 1000 samples which is indicated by the
relatively highly scattered values of
ˆ
σ
˜u
.
In fact observation(f) can be regarded as a premise for
considering regularization of the input noise variance
such that the uncertainty in the initial part of the iden-
tification is alleviated, leading to improved accuracy
of the estimates. In the second experiment the ERBFS
is compared with the RERBFS, where the parameters
are set as follows: ς = N/ω
0
where ω
0
= 100 and
σ
∗
˜u
= 1.5σ
˜u
. For completeness, the results obtained
by the BFS are also included. Consideration of the
results in Figure 3 leads to the following observations:
g) Although the guess of the regularization parame-
ter σ
∗
˜u
was rather ‘rough’, a substantial improve-
ment w.r.t. the input noise variance is observed in
the initial period of the recursion.
h) The impact of applying TR is also evident in the
case of the estimated output noise variance and
the system parameters leading to the faster con-
vergence.
i) Due to the utilization of the exponential control-
ling variable weighting ω
k
the results obtained by
the RERBFS and ERBFS at k = N are practically
indistinguishable. As a consequence, any poten-
tial induced bias due to the use of regularization
is kept to a minimum, for the case considered.
6 CONCLUSIONS
A new recursive technique, i.e. the RBBCLS method,
for identification of the class of SISO DBS has been
developedand evaluated. Within the RBBCLS frame-
work the ERBFS algorithm has been formulated in
which the Frisch equations are evaluated at each re-
cursion. The further extension incorporating the vari-
able regularization via the TR method, giving rise to
the RERBFS, was considered and shown to be bene-
ficial in the initial period of the identification proce-
dure. The methods proposed have been demonstrated
when applied to a SISO DBS EIV identification prob-
lem. Comparisons made with the standard RLS tech-
nique illustrates the superiority and relatively high
noise robustness of the proposed algorithms.
The further work will address two outstanding is-
sues. Firstly, the extension and subsequent recursive
implementation of the BCLS method to a wider class
of the polynomial nonlinear EIV systems. Secondly,
the alleviation of the computationalburden via the ap-
plication of a fully recursive BFS based on gradient
approaches and/or on other fast methods via lineariza-
tion of the Frisch equations.
REFERENCES
Beghelli, S., Guidorzi, R. P., and Soverini, U. (1990). The
Frisch scheme in dynamic system identification. Au-
tomatica, 26(1):171–176.
RECURSIVE BIAS-COMPENSATING ALGORITHM FOR THE IDENTIFICATION OF DYNAMICAL BILINEAR
SYSTEMS IN THE ERRORS-IN-VARIABLES FRAMEWORK
43

Burnham, K. J. (1991). Self-tuning Control for Bilinear Sys-
tems. PhD thesis, Coventry Polytechnic.
Diversi, R., Guidorzi, R., and Soverini, U. (2006). Yule-
Walker equations in the Frisch scheme solution of
errors-in-variables identification problems. In Proc.
of the 17th Int. Symposium on Mathematical Theory
of Networks and Systems, Kyoto, Japan.
Ekman, M. (2005). Modeling and Control of Bilinear Sys-
tems: Applications to the Activated Sludge Process.
PhD thesis, Uppsala University.
Hansen, P. C. (2001). Regularization tools: A matlab
package for analysis and solution of discrete ill-posed
problems. Technical report, Department of Mathemat-
ical Modelling, Technical University of Denmark.
Ikonen, E. and Najim, K. (2002). Advanced Process Identi-
fication and Control. Marcel Dekker, Inc., USA.
Kotta, U. and Nomm, S.and Zinober, A. (2003). On state
space realizability of bilinear systems described by
higher order difference equations. In Proc. of 42nd
IEEE Conf. on Decision and Control, volume 6, pages
5685–5690.
Larkowski, T., Linden, J. G., Vinsonneau, B., and Burnham,
K. J. (2008). A novel errors-in-variables approach for
bilinear models: the bilinear Frisch scheme. Internal
report no. CTAC/TL-1/2008, Control Theory and Ap-
plications Centre, Coventry University, Coventry.
Larkowski, T., Vinsonneau, B., and Burnham, K. J. (2007).
Bilinear model identification in the errors-in-variables
framework via the bias-compensating least squares. In
IAR and ACD Int. Conf., Grenoble, France.
Linden, G. J., Vinsonneau, B., and Burnham, K. J. (2007).
Fast algorithms for recursive Frisch scheme system
identification. In IAR and ACD Int. Conf., Grenoble,
France.
Liu, J. (1992). On stationarity and asymptotic inference of
bilinear time series models. Statistica Sinica, 2:479–
494.
Ljung, L. (1999). System Identification - Theory for the
User. Prentice Hall PTR, New Jersey, USA, 2nd edi-
tion edition.
Ljung, L. and S¨oderstr¨om, T. (1987). Theory and practice of
recursive identification. MIT Press, Cambridge, UK.
Martineau, S., Burnham, K. J., Haas, O. C. L., Andrews,
G., and Heeley, A. (2004). Four-term bilinear pid con-
troller applied to an industrial furnace. Control Engi-
neering Practice, 12(4):457–464.
Mohler, R. R. (1991). Nonlinear Systems: Applications to
Bilinear Control, volume 2. Prentice Hall, Englewood
Cliffs, NJ.
Mohler, R. R. and Khapalov, A. Y. (2000). Bilinear con-
trol and application to flexible a.c. transmission sys-
tems. Journal of Optimization Theory and Applica-
tions, 105(3):621–637.
Pearson, R. K. (1999). Discrete-Time Dynamic Models. Ox-
ford University Press, New York, USA.
Rao, T. S. and Gabr, M. M. (1984). An Introduction to
Bispectral Analysis and Bilinear Time Series Models.
Springer-Verlag, Berlin, Germany.
S¨oderstr¨om, T. (2006). Statistical analysis of the Frisch
scheme for identifying errors-in-variables systems.
Technical report, Upsala Univercity, Department of
Information Technology, Upsala, Sweden.
S¨oderstr¨om, T. (2007). Errors-in-variables methods in sys-
tem identification. In Automatica, volume 43, pages
939–958.
S¨oderstr¨om, T., Soverini, U., and Mahata, K. (2002). Per-
spectives on errors-in-variables estimation for dy-
namic systems. In Signal Processing, volume 82(8),
pages 1139–1154.
S¨oderstr¨om, T. and Stoica, P. (1994). System Identification.
Prentice Hall Int., New Jersey, USA.
Young, P. (1984). Recursive Estimation and Time-Series
Analysis. Springer-Verlag, Berlin, Germany.
Yu, D. (1996). Fault diagnosis for industrial systems with
emphasis on bilinear systems. PhD thesis, Coventry
University.
Zheng, W. X. (1998). Transfer function estimation from
noisy input and output data. Int. Journal of Adaptive
Control and Signal Processing, 12:365–380.
Zheng, W. X. (2000). Parametric identification of linear
noisy input-output systems. Cybernetics and Systems,
31(7):803–816.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
44
1000 2000 3000 4000 5000
−1.2
−1.1
−1
−0.9
1000 2000 3000 4000 5000
0.6
0.7
0.8
0.9
1000 2000 3000 4000 5000
0.45
0.5
0.55
0.6
1000 2000 3000 4000 5000
−0.1
0
0.1
0.2
a
1
a
2
b
1
η
11
NN
NN
BFS
ERBFS
true
RLS
1000 2000 3000 4000 5000
0.02
0.04
0.06
0.08
0.1
1000 2000 3000 4000 5000
0.12
0.14
0.16
0.18
1000 2000 3000 4000 5000
0.45
0.5
0.55
0.6
0.65
1000 2000 3000 4000 5000
1.4
1.6
1.8
σ
˜u
σ
˜y
σ
u
σ
y
NN
NN
Figure 2: The results of the identification procedure using ERBFS, BFS and RLS algorithms.
1000 2000 3000 4000 5000
−1.22
−1.21
−1.2
−1.19
−1.18
1000 2000 3000 4000 5000
0.9
0.91
0.92
0.93
1000 2000 3000 4000 5000
0.5
0.55
0.6
1000 2000 3000 4000 5000
0.1
0.12
0.14
0.16
a
1
a
2
b
1
η
11
NN
NN
RERBFS
BFS
ERBFS
1000 2000 3000 4000 5000
0.02
0.04
0.06
0.08
0.1
1000 2000 3000 4000 5000
0.13
0.14
0.15
0.16
0.17
0.18
σ
˜u
σ
˜y
N
N
Figure 3: The results of the identification procedure using BFS, RERBFS and ERBFS algorithms.
RECURSIVE BIAS-COMPENSATING ALGORITHM FOR THE IDENTIFICATION OF DYNAMICAL BILINEAR
SYSTEMS IN THE ERRORS-IN-VARIABLES FRAMEWORK
45
